Pregunta.
Demuestra el siguiente resultado: «Un triángulo cuyos lados pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1) es rectángulo».
Demuestra, mediante un contraejemplo, que el caso inverso es falso.
Respuesta.
Primero tenemos que determinar cuál es el lado mayor de un triángulo cuyos lados pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1).
n2 + 1 - 2n = (n - 1)2 y si n > 1 entonces (n - 1)2 > 0. Por tanto n2 + 1 - 2n > 0. Por tanto n2 + 1 > 2n.
Asimismo (n2 + 1) - (n2 - 1) = 2. Por tanto n2 + 1 > n2 - 1.
Eso significa que n2 + 1 es el lado mayor de un triángulo cuyos lados pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1).
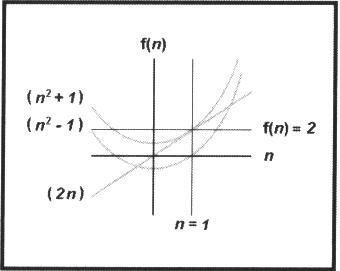
Esto puede mostrarse también mediante el siguiente gráfico (aunque esto no prueba nada):

Según el teorema de Pitágoras, si la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, el triángulo es rectángulo. Por lo tanto, para probar que el triángulo es rectángulo, necesitamos demostrar que ése es el caso.
La suma de los cuadrados de los dos catetos es
(n2 - 1)2 + (2n)2=(n2 - 1)2 + (2n)2=
n4 - 2n2 + 1 + 4n2 = n4 + 2n2 + 1.
El cuadrado de la hipotenusa es (n2 + 1)2 y (n2 + 1)2 = n4 + 2n2 + 1.
Por tanto la suma de los cuadrados de los dos catetos es igual al cuadrado de la hipotenusa, y el triángulo es rectángulo.
Y lo inverso a «Un triángulo cuyos lados pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1) es rectángulo» es «Un triángulo que es rectángulo tiene unos lados cuyas longitudes pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1)».
Y un ejemplo opuesto significa encontrar un triángulo que sea rectángulo, pero cuyos lados no puedan escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1).
Así, pongamos que la hipotenusa del triángulo rectángulo ABC sea AB y pongamos que AB = 65 y pongamos que BC = 60. Entonces
CA = √ ((AB)2-(BC)2)=√ (652 - 602) =
√ (4.225 - 3.600) = √ 625 = 25.
Pongamos que AB = n2 + 1 = 65. Entonces n = √ (65 - 1) = √ 64 = 8. Por tanto (n2 - 1) = 64 - 1 = 63 ≠ BC = 60 ≠ CA = 25. Y 2n = 16 ≠ BC = 60 ≠ CA = 25.
Por lo tanto el triángulo ABC es rectángulo pero sus lados no pueden escribirse en la forma n2 + 1, n2 - 1 y 2n (donde n > 1). QED