33. Las gansadas se pagan

EL JUEGO DE LAS POSICIONES

Con muchachos tan escandalosos como Alberto y sus amigos, lo raro es no encontrárselos formando algún caos. Esto es algo que se puede dar especialmente al comienzo de una nueva asignatura cuatrimestral, justo antes de la entrada del profesor novato. Esta vez, el barullo se formó cuando un compañero de Alberto inició una verdadera guerra de guerrillas armado de un canuto vacío de boli a modo de cerbatana, y utilizando como temible munición unos granos de arroz. En unos instantes los ocho alumnos más conflictivos se encontraron bombardeándose los unos a los otros, cambiando continuamente de pupitre y posición.

Cuando entró en la clase, el nuevo profesor se echó las manos a la cabeza. Tenía fama de ser un viejo cascarrabias, pero sobre todo de ser algo retorcido, según les habían comentado los alumnos del curso superior. Así pues, la cosa estaba clara y el castigo servido.

Como la gansada se basaba en un cambio de posición permanente, el castigo no pudo ser menos. Consistía en irse colocando en los sesenta y cuatro pupitres que tenía la clase, que estaban repartidos en ocho filas de ocho pupitres cada una, pero haciéndolo de tal forma que ninguno de los ocho permaneciera alineado ni vertical, ni horizontal, ni siquiera diagonalmente con sus otros siete compañeros de «guerrillas».

—Para que os vayáis enterando os doy un ejemplo de solución, mis queridos alumnos —dijo satisfecho el profesor al ver la perplejidad de Alberto y sus amigos.

En el pupitre D4 se colocó Alberto, y la disposición que compuso con los otros siete alumnos aparece igualmente reflejada en el dibujo. Es posible establecer una norma de numeración para distinguir unas soluciones de otras. De este modo, la descrita por el profesor podríamos llamarla 25741863. Y esto, si consideramos la posición de cada alumno sucesivamente en cada una de las columnas ABCDEFGH.

«¡Ondiá!, a fin de cuentas esto se parece al ajedrez», pensó Alberto.

Cuando el profesor comprobó que los ocho revoltosos habían comprendido, dijo:

—Pues bien, la primera pregunta es ésta:

—Efectivamente, hay varias, más de diez e incluso más de cincuenta. La cuestión es saber cuántas son exactamente, ni una más ni una menos —descubrió el bueno de Alberto.

—¡Ah!, queridos alumnos, tendréis que considerar como soluciones diferentes sólo aquellas que no se pueden conseguir girando la clase, como si efectivamente fuese un tablero de ajedrez —añadió el profesor—, y tampoco consideraréis distintas las que puedan verse como reflejadas en un espejo. ¡Tienen que ser auténticamente diferentes!

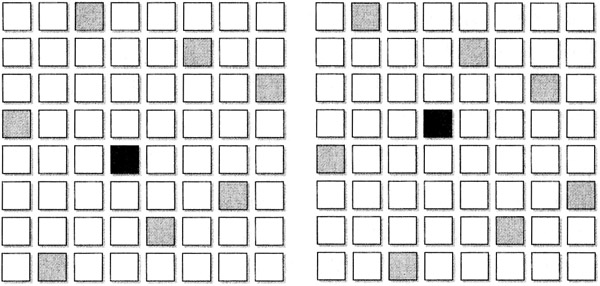
Las dos posiciones de la figura son, en definitiva, la misma que compuso el profesor si nos atenemos a lo expuesto; por tanto no serían válidas.

Alberto encontró rápidamente la solución. Por ello, el profesor no se quedó demasiado satisfecho con el resto de los revoltosos, de modo que les preguntó:

—Si Alberto se mantiene en la posición que ocupa, es decir, la D4, mientras vosotros os cambiáis de sitio,