Fig. 1
¿Puede la Ciencia aportar información en materia de Religión? ¿Pueden los resultados de la investigación científica ser de alguna ayuda para conseguir una actitud razonable y satisfactoria frente a estas cuestiones ardientes que a todos nos asaltan en algún momento? Algunos de nosotros, en una juventud particularmente sana y feliz, hemos conseguido alejarlas por largos períodos de tiempo; otros, en edad avanzada, se han convencido de que no existe respuesta y se han resignado a renunciar, mientras que otros se han obsesionado con esta incongruencia durante toda la vida, preocupados con serios temores aumentados por la superstición popular y tradicional. Me refiero sobre todo a las cuestiones del «otro mundo», a la «vida después de la muerte» y todo lo que se relaciona con ello. No se crea por favor que voy a intentar contestar a estas cuestiones, sino tan sólo a la más modesta, es decir, discutir hasta dónde puede la Ciencia aportar información o ayudarnos a reflexionar sobre ellas, dado que somos muchos los que no podemos evitarlas.
Para empezar, la Ciencia puede, aunque de manera muy primitiva, ayudamos con estas cuestiones. Veamos un ejemplo. Recuerdo antiguos grabados y mapas geográficos del mundo que representaban el infierno, el purgatorio y el cielo, el primero situado profundamente bajo tierra, el último en lo alto de los cielos. Estas representaciones no eran simples alegorías (como podían serlo, en períodos posteriores, por ejemplo, la famosa Adoración a la Santísima Trinidad de Durero) y son testimonio de una tosca creencia bastante popular en la época. Naturalmente, ninguna Iglesia exige de la fe una interpretación tan materialista de sus dogmas, incluso desalentaría seriamente semejante actitud. Este progreso ha sido ciertamente favorecido por nuestro conocimiento del interior del planeta (aunque sea escaso), de la naturaleza de los volcanes, de la composición de nuestra atmósfera, de la probable historia del sistema solar y de la estructura de la galaxia y del universo. No hay persona cultivada que espere encontrar estas quimeras dogmáticas en alguna parte del espacio accesible a nuestras investigaciones, ni siquiera, me atrevería a decir, en las regiones que continúan ese espacio, pero que son inaccesibles a la investigación; todo hombre culto les daría, incluso en el caso de que esté convencido de su realidad, un carácter espiritual. No pretendo decir con esto que las personas profundamente religiosas deban estar a la espera de estos logros de la Ciencia, pero no hay duda de que han colaborado a erradicar la superstición materialista de estas cuestiones.
Sin embargo, esto se refiere a un estado bastante primitivo de la mente. Existen puntos de mayor interés. Las contribuciones más importantes de la Ciencia para vencer las misteriosas preguntas: ¿quiénes somos realmente?, ¿de dónde vengo y adónde voy? —o al menos para que nuestras mentes se tranquilicen—, digo, la ayuda más apreciable de la Ciencia acaso sea la idealización gradual del tiempo. Tres nombres se imponen en este tema (aunque muchos otros, incluyendo no científicos, han alcanzado una importancia del mismo calibre como San Agustín de Hipona y Boecio); los tres nombres son Platón, Kant y Einstein.
Los dos primeros no fueron científicos, pero su penetrante dedicación a las cuestiones filosóficas, su interés absorbente por el mundo dieron lugar a la Ciencia. Platón partió de las Matemáticas y de Geometría (la conjunción «y» estaría hoy fuera de lugar, pero no lo está, creo, en este caso). ¿Qué es lo que ha distinguido la obra de Platón para que su esplendor se mantenga después de más de dos mil años? Por lo que sabemos, no nos descubrimientos especiales sobre números ni figuras geométricas. Su comprensión del mundo material de la Fínica y de la vida es a veces fantástico e inferior, en conjunto, a los de otros (los sabios desde Tales a Demócrito) que vivieron, algunos de ellos, más de un siglo, en tiempos anteriores al suyo; en el conocimiento de la Naturaleza fue ampliamente superado por su discípulo Aristóteles y por Teofrasto. Casi todos los largos pasajes de sus diálogos dan la impresión de ser gratuitos juegos de palabras. No hay intención de definir el significado de una palabra, sino más bien la creencia de que la propia palabra acabará por descubrir su contenido, si le damos suficientes vueltas. Su utopía social y política, que le puso en grave peligro cuando intentó promocionarla para la práctica, tiene pocos admiradores hoy en día. ¿A qué se debe, entonces, su fama?
Se debe, en mi opinión, a que fue el primero en vislumbrar la idea de una existencia sin tiempo y en recalcarla —contra la Razón— como una realidad más real que nuestra auténtica experiencia; ésta, dijo, no es más que una sombra de la primera; toda realidad experimentada se toma de aquélla. Me refiero a la teoría de las formas (o de las ideas). ¿Cuál fue su origen? No cabe duda de que ésta germinó gracias a las enseñanzas de Parménides y de los Eleáticos. Pero igualmente obvio es que Platón encontró con ello una vena viva y atractiva —algo muy en la línea del hermoso símil de Platón según el cual aprender por la razón equivale a recordar un conocimiento, previamente poseído pero latente, y no tanto el camino hacia verdades enteramente nuevas. Sin embargo, el Ser eterno, omnipotente y único de Parmenides se convirtió, en la mente de Platón, en un pensamiento mucho más potente, la Esfera de las Ideas, que apela a la imaginación aunque permanece necesariamente en el misterio. Pero este pensamiento saltó, creo, de una experiencia muy real, por la admiración y respeto que en él despertaron las revelaciones en el dominio de los números y de las figuras geométricas. Lo mismo había ocurrido antes con los pitagóricos y había de ocurrir luego con otros muchos. Reconoció y asimiló profundamente en su mente la Naturaleza de estas revelaciones (que se desarrollaron por un razonamiento puramente lógico) y nos enseñó las relaciones verdaderas cuya verdad no es sólo irrebatible, sino que ahí está obviamente para siempre. Una verdad matemática es atemporal, no se asocia con el Ser por el hecho de ser descubierta. Pero su descubrimiento es un hecho muy real, puede ser una emoción similar a la de un premio gordo de la lotería.
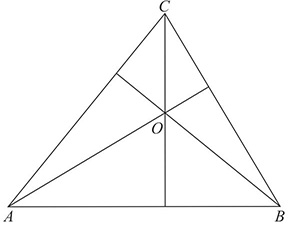
Las tres alturas de un triángulo (ABC) se encuentran en un punto (O). (Altura es la perpendicular trazada desde un vértice hasta el lado opuesto o hasta su prolongación).

Fig. 1
A primera vista, no vemos la razón por la que esto deba ser así. Tres rectas cualesquiera no tienen por qué converger en un punto, en general forman un triángulo. Tracemos ahora una paralela a cada lado que pase por el vértice opuesto y formaremos un triángulo mayor A’B’C’. Éste se compone de cuatro triángulos semejantes[14]. Las tres alturas de ABC son, en A’B’C’, las perpendiculares que pasan por los puntos medios de los lados, «sus mediatrices». Ahora bien, la que pasa por C contiene todos los puntos que equidistan de A’ y B’; la que pasa por B contiene todos los puntos que equidistan de A’ y C’ Por lo tanto, el punto donde ambas se cortan debe equidistar de todos los vértices, A’, B’ y C’, por lo que deben pertenecer también a la perpendicular que pasa por A, ya que ésta contiene todos los puntos que equidistan de B’ y C’ Q.E.D.[15].
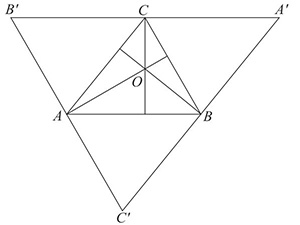
Fig. 2
Cada número entero, excepto el 1 y el 2, es el «punto medio» de dos números primos, o bien, su valor medio, por ejemplo:
8 = ½(5 + 11) = ½(3 + 13)
17 = ½(3 + 31) = ½(29 + 5) = ½(23 + 11)
20 = ½(11 + 29) = ½(3 + 37)
En general existe, como vemos, más de una solución. Se trata del teorema de Goldbach; se supone que es cierto, aunque no ha sido demostrado.
Sumando los números consecutivos impares empezando por el uno (1 + 3 = 4; 1 + 3 + 5 = 9; 1 + 3 + 5 + 7 = 16), obtenemos siempre cuadrados perfectos[16] y, en efecto, por este procedimiento, se obtiene además el cuadrado del número de números impares que hemos sumado. Para captar la generalidad de esta relación sustituyamos en la suma aquellas parejas de sumandos que equidistan del centro (es decir, el primero y el último, el segundo y el penúltimo, etc.) por su media aritmética, que es evidentemente igual al número de sumandos. Para el último ejemplo sería:
4 + 4 + 4 + 4= 4 × 4
Ahora volvamos a Kant. Kant nos mostró la identidad del espacio y del tiempo, y que ello era fundamental, acaso lo más fundamental de su enseñanza. Esto, como casi toda su enseñanza, no puede ser ni comprobado ni falseado, pero no por ello pierde interés (más bien gana; sería trivial si pudiese ser demostrado o refutado). Significa lo siguiente: el que algo se propague en el espacio o el que algo suceda en un tiempo bien definido de «antes y después», no es una cualidad del mundo que percibimos, sino que pertenece a la mente perceptora que (de algún modo en su situación actual) se ve incapaz de registrar nada de lo que se le ofrece si no es según este esquema espacio-temporal. Esto no quiere decir que la mente comprenda estos esquemas de orden sin la consideración previa de la experiencia, sino que no puede colaborar a su desarrollo ni a su aplicación a la experiencia, y, particularmente, que ello no prueba ni sugiere que el espacio y el tiempo constituyen un esquema de orden inherente a «la cosa en sí» que, como algunos creen, es causa de nuestra experiencia.
No es difícil tomar la postura de que esto es un disparate. Nadie puede hacer una distinción entre la esfera de sus percepciones y el mundo de las cosas que causa la primera, ya que, a pesar del conocimiento detallado que podemos adquirir de la historia global, la historia acontece sólo una vez, no dos veces. La duplicación es una alegoría, sugerida sobre todo por la comunicación con otros seres humanos e incluso con animales. En efecto, esta comunicación nos muestra que sus percepciones parecen, en la misma situación, muy similares a las propias, excepción hecha de algunas insignificantes diferencias en el punto de vista (en el sentido literal de «punto de proyección»). Pero aun suponiendo, como todos hacen, que esto nos obliga a considerar un mundo objetivamente existente como la causa de nuestras percepciones, ¿cómo asegurar en este mundo que un hecho común de toda nuestra experiencia se debe más a la constitución de nuestra mente, que a una cualidad compartida por todas esas cosas objetivamente existentes? Nuestras percepciones sensoriales constituyen, es cierto, nuestro único conocimiento sobre las cosas. El mundo objetivo se queda en una hipótesis, aunque ésta es natural. Si la adoptamos, ¿no será mucho más lógico atribuir a este mundo exterior, y no a nosotros mismos, todas estas características que las percepciones sensoriales en él encuentran?
Sin embargo, la suprema importancia de la afirmación de Kant no consiste precisamente en repartir los papeles de la mente y de sus objetivos —el mundo— en el proceso mediante el cual «la mente se forma una idea del mundo», porque, como he señalado, difícilmente distinguiremos los dos conceptos. Lo grandioso es concebir la idea de que esa cosa única —mente o mundo— pueda ser capaz de otras formas de apariencia que no podemos captar y que no implican las nociones de espacio y tiempo. Esto supone una liberación impuesta a nuestros prejuicios habituales. Seguramente existen otros órdenes de apariencia aparte de los espacio-temporales. Schopenhauer fue el primero, creo, en saber detectar esto en Kant. Esta liberación abre el camino para creer, en el sentido religioso, sin tener que habérselas continuamente con los claros resultados que la inconfundible experiencia pronuncia sobre el mundo. Por ejemplo —para citar el caso más trascendente—, la experiencia, dado que la consideramos inconfundible, produce la convicción de que ella misma no puede sobrevivir a la destrucción del cuerpo, con cuya vida (tal como entendemos la vida) está inseparablemente ligada. Entonces, ¿no hay nada después de la vida? No. No en la forma necesariamente espacio-temporal de la experiencia. Pero, en un orden de apariencia en el que no juega el tiempo, esta noción de «después» carece de sentido. El pensamiento puro no puede, claro, brindamos una garantía de que algo así existe. Pero puede eliminar los obstáculos aparentes para que podamos concebirlo como posible. Esto es lo que Kant ha conseguido con sus análisis y esto es, para mí, su importancia filosófica.
Le toca ahora el turno a Einstein en este mismo contexto. La actitud de Kant con respecto a la Ciencia era increíblemente ingenua; véanse, si no, sus Fundamentos metafísicos de la Ciencia[17]. Aceptaba la Física en la forma que ésta había alcanzado durante su vida (1724-1804), como algo más o menos final, y se ocupaba de dar cuenta filosófica de sus leyes. Que esto le pasara a un gran genio debía ser una advertencia para todos los filósofos posteriores. Mostró claramente que el espacio era necesariamente infinito y creyó firmemente que, en la naturaleza de la mente humana, estaba el dotarla de las propiedades geométricas enunciadas por Euclides. Este espacio euclídeo cambió su configuración con el tiempo. Para Kant, como para cualquier físico de su época, espacio y tiempo eran dos conceptos enteramente distintos, por lo que no tuvo duda alguna a la hora de denominar el espacio como la forma de nuestra intuición externa, y el tiempo como la forma de nuestra intuición interna (Anschauung). El reconocimiento de que el espacio infinito de Euclides no representa un camino necesario para observar el mundo de nuestra experiencia, y este espacio-tiempo, considerado como un continuo de cuatro dimensiones, parece pulverizar los fundamentos de Kant (aunque en verdad no afecta la parte más valiosa de su filosofía).
Este reconocimiento quedó para Einstein (y algunos otros, Lorentz, Poincaré y Minkowski, por ejemplo). El poderoso impacto, que sus descubrimientos tuvieron entre filósofos, hombres de la calle y amas de casa, se debe a que ellos mismos los trajeron a la palestra: incluso en el dominio de nuestra experiencia, las relaciones espacio-temporales son mucho más intrincadas de lo que Kant soñara y con esto estuvieron de acuerdo todos los físicos anteriores, hombres de la calle y amas de casa.
El impacto más fuerte de la nueva idea se produce en la anterior noción de tiempo. El tiempo es la noción del «antes y después». La nueva actitud surge de las dos raíces siguientes:
1.- La noción del «antes y después» reside en la relación de «causa y efecto». Sabemos, o al menos hemos concebido la idea de que un hecho A puede causar, o al menos modificar, otro hecho B, de forma que si A no fuera, entonces tampoco lo sería B, no al menos en esta forma modificada. Por ejemplo, cuando explota una granada, ésta mata al hombre que se sienta encima; la explosión se oye, además, en lugares distantes. La muerte puede ser simultánea con la explosión; no obstante, la recepción del sonido en un lugar distante ocurrirá más tarde, aunque no haya ciertamente efectos anteriores. He aquí un concepto básico; en efecto, en la vida cotidiana, lo utilizamos para decidir cuál de los dos hechos es posterior o, al menos, para decidir cuál de los dos no es anterior. La distinción se basa enteramente en la idea de que el efecto no puede preceder la causa. Si tenemos razones para pensar que B ha sido causado por A, o que al menos muestra vestigios de A, o incluso se concibe (de cierta evidencia circunstancial) que muestra estos vestigios, entonces se determina que B no puede ser anterior a A.
2.- Téngase esto presente. La segunda raíz es la evidencia (de la experiencia y de la observación) según la cual los efectos no se propagan a una velocidad arbitrariamente alta. Existe un límite superior fijado por la velocidad de la luz en el vacío. Se trata de un valor muy grande a escala humana (siete vueltas a la tierra en un segundo). Muy grande, pero no infinito, llamémoslo c. Admitamos este hecho como fundamental en la Naturaleza. Resulta entonces que la distinción antes mencionada entre el «antes y el después» o entre el «anterior y posterior» (conceptos basados en la relación de causa-efecto) no puede aplicarse universalmente, falla en algunos casos. No es fácil de explicar sin recurrir al lenguaje matemático. No es que el esquema matemático sea tan complicado, sino que el lenguaje cotidiano está demasiado condicionado por la noción de tiempo, no puede usarse un verbo (verbum, «la palabra», en alemán: Zeitwort[18]) sin utilizarlo en uno u otro sentido.
La consideración más simple (aunque no del todo adecuada) es la que sigue. Sea un hecho A. Consideremos para cualquier instante posterior un hecho B, exterior a la esfera y con centro en A y radio ct. El hecho B no puede exhibir «vestigio» alguno de A ni, por supuesto, puede hacerlo A de 8. Nuestro criterio ha fallado. Hemos utilizado el lenguaje para decir que B es posterior. Pero ¿estamos en lo cierto en esto, si el criterio nos falla en cualquiera de los casos?
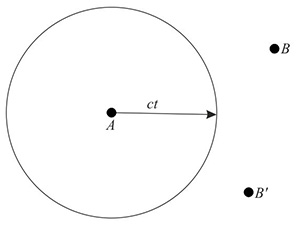
Fig. 3
Consideremos, para tiempos anteriores, un suceso B’ fuera de la misma esfera. En este caso, como en el anterior, ningún vestigio de B’ puede haber alcanzado a A (y, por supuesto, ninguno de A puede exhibirse en B’).
En los dos casos existe la misma relación de mutua no-interferencia. No existe diferencia conceptual alguna entre dos clases de sucesos B y B’ con respecto a sus relaciones causa-efecto con A. Así, si queremos establecer esta relación, y no un prejuicio lingüístico (la base del «antes y después»), entonces B y B’ forman un solo tipo de hechos que no son ni anteriores ni posteriores a A. La región del espacio-tiempo ocupado por este tipo se llama «simultaneidad potencial» (con respecto al hecho A). Se emplea esta expresión porque siempre puede adoptarse un sistema espacio-temporal que haga A simultáneo con un B o B’ elegido en particular. Éste fue el descubrimiento de Einstein (conocido como la Teoría Especial de la Relatividad, 1905).
Todas estas cosas se han convertido en una realidad muy concreta para nosotros los físicos, las empleamos cada día en nuestro trabajo, del mismo modo que la tabla de multiplicar o el teorema de Pitágoras. A veces me maravillo del revuelo que han organizado entre el público en general y entre los filósofos. Supongo que la razón está en esto, en el derrocamiento del tiempo como rígido tirano, impuesto desde el exterior, en que nos hemos liberado de la indestructible regla del «antes y después». Pues, el tiempo es, en efecto, nuestro amo más severo al acotar aparentemente nuestra existencia dentro de estrechos límites (setenta u ochenta años). Poder jugar con ello, utilizando un programa maestro —que hasta entonces creíamos inaccesible—, poder jugar aunque sea modestamente, parece tener una gran importancia, parece alentar la idea de que la «tabla del tiempo» global no es seguramente tan seria como parecía a primera vista. Y esta idea es una idea religiosa; más aún, yo la llamaría la idea religiosa.
Einstein no ha refutado —como en ocasiones oímos— las profundas ideas de Kant sobre la idealización del espacio y del tiempo; ha dado, por el contrario, un gran paso hacia su consecución.
He hablado del impacto de Platón, Kant y Einstein desde el punto de vista de la Filosofía y de la Religión. Pero, entre Kant y Einstein, más o menos una generación antes del último, la Física fue testigo de un acontecimiento trascendental que en principio debería haber conmocionado también a filósofos, hombres de la calle y amas de casa, por lo menos (si no más) tanto como la Teoría de la Relatividad. Si no fue así, se debe, creo, al hecho de que ello es aún más difícil de comprender; muy pocas de las personas de las anteriores categorías captaron las nuevas ideas, algún filósofo todo lo más. Este acontecimiento se asocia a los nombres del americano Willar Gibbs y del austríaco Ludwig Boltzmann. Quiero decir unas palabras sobre el tema.
El curso de los acontecimientos en la Naturaleza es, con raras excepciones (suponiendo que realmente lo sean), irreversible. Si intentamos imaginar una sucesión temporal de fenómenos exactamente opuesta a la sucesión que realmente observamos —una película proyectada en sentido contrario, por ejemplo—, veremos que esta sucesión invertida (aunque fácil de imaginar entra en grave contradicción con las bien establecidas leyes de la Física.
El «tropismo» (directness) de todo acontecer se explicó mediante la teoría matemática o estadística del calor, una explicación que fue acogida como su logro más admirable. No puedo entrar aquí en los detalles de la teoría física, pero ello no es necesario para hacerse cargo de la esencia de esta explicación. Ésta sería muy pobre si la irreversibilidad hubiese sido introducida como una propiedad fundamental del mecanismo microscópico de los átomos y de las moléculas. No hubiese sido mejor que muchas explicaciones medievales puramente verbales como: el fuego está caliente a causa de su fogosa cualidad. No, según Boltzmann, estamos ante la tendencia natural de todo sistema a evolucionar desde un estado ordenado hacia otro menos ordenado, pero no en el sentido inverso. Consideremos como símil una baraja de cartas de juego que ordenamos cuidadosamente en la forma: 7, 8, 9, 10, sota, dama, rey y as de corazones, lo mismo con los tréboles, etc. Si barajamos una, dos o tres veces esta baraja bien ordenada, se convertirá en un conjunto gradualmente desordenado de cartas. Pero no se trata de una propiedad intrínseca del proceso de barajar. Puede pensarse perfectamente que, barajando el desordenado conjunto resultante, se consiga cancelar exactamente el efecto de la primera operación, con lo que se recuperaría el orden original. Sin embargo, todo el mundo se espera el primer proceso, nadie el segundo (haría falta esperar, en efecto, un tiempo muy largo para que ello ocurriese por azar).
Ésta es, pues, la esencia de la aplicación de Boltzmann sobre el carácter unidireccional de todo aquello que ocurre en la Naturaleza (incluyendo, claro, la historia de la vida de un organismo desde el nacimiento hasta la muerte). Su virtud más importante es que «la flecha del tiempo» (como Eddington la llamó) no tiene en cuenta los mecanismos concretos de interacción que, en nuestra analogía, se representa por el acto mecánico de barajar. Este acto, este mecanismo, está exento de toda noción de pasado y futuro, es completamente reversible, la «flecha» —la misma noción de pasado y futuro— resulta de consideraciones estadísticas. En nuestra analogía de las cartas, todo reside en que sólo hay una, o muy pocas agrupaciones bien ordenadas, mientras que existen miles de millones de agrupaciones desordenadas.
A pesar de todo, esta teoría se encuentra, una y otra vez, con la ocasional oposición de eminentes pensadores. La oposición se reduce a lo siguiente: la teoría se considera defectuosa desde el punto de vista lógico. Pues, se dice, si los mecanismos básicos no distinguen entre las dos direcciones del tiempo, sino que funcionan simétricamente con respecto a él, ¿cómo es que de su cooperación resulta un comportamiento conjunto e integrado fuertemente polarizado en una sola dirección? Todo lo que vale para esta dirección ha de valer igualmente para la opuesta.
La solidez de este argumento parece fatal para la teoría, ya que apunta precisamente contra el punto que hemos considerado de mayor mérito: obtener procesos irreversibles de mecanismos básicos reversibles.
El argumento es perfectamente sólido pero no es fatal. El argumento es sólido por cuanto afirma que lo que vale en una dirección del tiempo también vale en la opuesta (un tiempo introducido desde el principio como variable perfectamente simétrica). Pero no puede deducirse de ello que vale, en general, para ambas direcciones. Cuidando las palabras, puede decirse que el tiempo es simétrico para cada caso particular. Y debe añadirse: la degeneración del mundo que conocemos tiene lugar en una dirección; y la denominamos como la que va del pasado al futuro. En otras palabras, debemos permitir que la teoría estadística del calor decida en qué dirección fluye el tiempo (esto tiene una importancia enorme para la metodología del físico, ya que éste no puede introducir nada que decida la flecha del tiempo independientemente; de otro modo, el hermoso edificio de Boltzmann se viene abajo).
Puede temerse que la definición estadística del tiempo no resulte siempre en la misma dirección temporal para distintos sistemas físicos. Boltzmann consideró audazmente esta eventualidad; mantuvo que el universo es lo suficientemente grande y/o que existe por un período lo bastante largo para que el tiempo pueda realmente fluir (en lugares muy distantes) en la dirección opuesta. Este punto fue argumentado, pero difícilmente puede serlo hoy en día. Boltzmann desconocía algo que para nosotros es, cuando menos, familiar: el universo, tal como lo conocemos, no es lo bastante grande ni antiguo como para que estas inversiones temporales tengan lugar a gran escala. Pido se me permita añadir —sin explicaciones detalladas— que, en una escala muy pequeña, estas inversiones (para el espacio y para el tiempo) han sido observadas (Movimiento browniano, Smolnakowski).
En mi opinión, la Teoría Estadística del Tiempo tiene incluso más relación con la Filosofía del Tiempo que con la Teoría de la Relatividad. Esta última, aunque revolucionaria, deja la unidireccionalidad del tiempo intacta (se presupone), mientras que la Teoría Estadística la establece a partir del orden de los hechos. Esto supone liberarse de la tiranía del viejo Chronos. Lo que construimos en nuestras mentes no puede tener (así lo siento) un poder dictatorial sobre nuestra mente, no puede cuestionarla ni aniquilarla. Algunos de ustedes dirán, estoy seguro, que esto es misticismo. Así, aun reconociendo que las teorías de la Física son siempre relativas —por cuanto dependen de ciertas hipótesis básicas—, podemos afirmar, o así lo creo, que las teorías actuales de la Física sugieren fuertemente la indestructibilidad de la Mente frente al Tiempo.