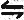Apéndice

Los colores del infinito

En noviembre de 1989, al recibir el premio por logros especiales de la Asociación de Exploradores del Espacio en Riad, Arabia Saudí, tuve el privilegio de hablar ante la mayor reunión de astronautas y cosmonautas que se haya congregado jamás. (Más de cincuenta, entre ellos Buzz Aldrin y Mike Collins, del Apolo 11, y Alexei Leonov, el primer «caminante espacial», que ya no se siente en un compromiso por compartir la dedicatoria de 2010: odisea dos con Andrei Sajarov). Decidí expandir sus horizontes presentándoles algo realmente grande y, bajo la égida del príncipe Sultan bin Salman bin Abdul Aziz, astronauta, dicté una conferencia llena de ilustraciones: «Los colores del infinito: explorando el universo fractal».

El material que sigue está extraído de esa charla; otra parte figura al comienzo del capítulo 15. Sólo lamento que no pueda ilustrarla con las espléndidas diapositivas de 35 milímetros y vídeos que usé en Riad.

Hoy todos están familiarizados con los gráficos, sobre todo el que presenta el tiempo en un eje horizontal, y el coste de vida subiendo sin cesar en el vertical. La idea de que cualquier punto de un plano se puede expresar con dos números, habitualmente denominados x e y, hoy parece tan obvia que resulta sorprendente que el mundo de las matemáticas haya tenido que esperar a que Descartes la inventara en 1637.

Aún estamos descubriendo las consecuencias de esa idea aparentemente sencilla, y la más asombrosa de ellas sólo tiene diez años. Se llama «conjunto de Mandelbrot» (a partir de aquí, «conjunto M») y pronto lo encontraremos por doquier: en telas, empapelados, joyas y linóleos. También me temo que aparecerá en muchos anuncios de TV.

El rasgo más asombroso del conjunto M es su simplicidad. A diferencia de todo lo demás en las matemáticas modernas, cualquier niño puede entender cómo se genera. Sólo se requiere suma y multiplicación; no se necesitan complejidades tales como la resta y —Dios nos guarde— la división, y mucho menos otros animales exóticos del zoológico matemático.

Hay poca gente en el mundo civilizado que no se haya topado con la famosa fórmula E = mc² de Einstein, o que la considere tan enrevesada como para que le resulte incomprensible. Pues la ecuación que define el conjunto M contiene la misma cantidad de términos, y se ve muy similar. Hela aquí:

Z = z² + c

No es muy aterradora, ¿verdad? Pero la vida del universo no alcanzaría para explorar todas sus ramificaciones.

Las zetas y la c de la ecuación de Mandelbrot son números, no cantidades físicas como masa y energía (como en la ecuación de Einstein). Son las coordenadas que especifican la posición de un punto, y la ecuación controla el modo en que éste se mueve para trazar una figura.

Hay una sencilla analogía que todo el mundo conoce: esos libros para niños con páginas en blanco salpicadas de números, que revelan imágenes ocultas —y a menudo asombrosas— cuando se unen en el orden correspondiente. La imagen de una pantalla de TV se genera mediante una aplicación refinada del mismo principio.

En teoría, cualquiera que pueda sumar y multiplicar podría describir el conjunto M con pluma o lápiz en una hoja de papel cuadriculado. Sin embargo, como veremos después, existen algunas dificultades prácticas, sobre todo el hecho de que una vida humana rara vez dura más de cien años. Así que el conjunto siempre se genera por ordenador, y normalmente se muestra en una pantalla.

Ahora bien, hay dos modos de localizar un punto en el espacio. El más común emplea una especie de referencia por coordenadas: este-oeste, norte-sur, o, en papel cuadriculado, un eje horizontal X y un eje vertical Y. Pero también está el sistema que se utiliza en el radar, hoy conocido por mucha gente gracias al cine. Aquí la posición de un objeto es dada por (1) su distancia respecto del origen, y (2) su dirección o rumbo. Por cierto, éste es el sistema natural, el que se usa automática e inconscientemente cuando se juega a cualquier juego de pelota. En tal caso, uno se concentra en distancias y ángulos, y uno mismo es el origen.

Pensemos en el ordenador como una pantalla de radar, con una sola señal en ella, cuyos movimientos trazarán el conjunto M. Pero antes de encender el radar, quiero simplificar aún más la ecuación, de este modo:

Z = z²

He eliminado c por el momento, y sólo he dejado las zetas. Ahora las definiré con mayor precisión.

La zeta minúscula representa el rango inicial de la señal, la distancia a la que empieza. La zeta mayúscula es su distancia final desde el origen. Así, si inicialmente estaba a 2 unidades de distancia, al obedecer esta ecuación pronto brincará a una distancia de 4.

Nada demasiado emocionante, pero ahora viene la modificación que lo cambia todo:

Z 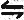z²

Esa doble flecha es una señal de tráfico en dos sentidos, e indica que los números fluyen en ambas direcciones. Esta vez no nos detenemos en Z = 4; lo hacemos equivaler a una nueva z, y pronto obtenemos una segunda Z de 16, y así sucesivamente. En poco tiempo hemos generado la serie

256, 65536, 4294967296 …

El lugar que empezó a sólo 2 unidades del centro se dirige al infinito a pasos agigantados de magnitud creciente.

Este proceso de ejecutar un bucle una y otra vez se llama «iteración». Es como un perro mordiéndose la cola, salvo que el perro no va a ninguna parte. La iteración matemática, en cambio, puede llevarnos a lugares muy extraños, como pronto descubriremos.

Ahora estamos listos para encender nuestro radar. La mayoría de las pantallas tienen rangos circulares de 10, 20… 100 kilómetros a partir del centro. Nosotros necesitaremos un solo círculo, con un rango de 1. No es preciso especificar ninguna unidad, pues estamos trabajando con números puros. Pueden ser centímetros o años luz, lo que gusten.

Supongamos que la posición inicial de nuestra señal está en cualquier parte de este círculo, sin que importe el rumbo. Así que z es 1.

como 1 al cuadrado sigue siendo 1, lo mismo pasa con Z. Y conserva ese valor, pues por mucho que elevemos 1 al cuadrado, siempre es 1. La señal puede brincar dentro del círculo, pero siempre permanece en él.

Ahora pensemos en el caso en que la z inicial es mayor que 1. Ya hemos visto cuán rápidamente la señal se dispara al infinito si z equivale a 2, pero lo mismo sucederá tarde o temprano, aunque sea apenas una microscópica fracción mayor que 1, por ejemplo, 1,000000000000000000001. Veamos. Con la primera elevación al cuadrado, Z se transforma en

1,000000000000000000002

Luego

Y así sucesivamente, durante páginas y páginas. En la práctica, el valor sigue siendo 1. La señal no se ha movido visiblemente hacia fuera ni hacia dentro; todavía está en el círculo, en el rango 1.

Pero esos ceros son devorados lentamente mientras los dígitos marchan inexorablemente desde la derecha. De pronto, algo aparece en los lugares decimales tercero, segundo, primero… y los números estallan al cabo de algunos términos adicionales, como lo demuestra este ejemplo:

Podría haber un millón o mil millones de ceros a la derecha y el resultado seguiría siendo el mismo. Con el tiempo los dígitos ascienden hasta la coma decimal y luego Z se dispara al infinito.

Ahora miremos el otro caso. Supongamos que z es una cantidad microscópica menor que 1, digamos:

0,99999999999999999999

Como antes, durante largo rato no pasan muchas cosas mientras ejecutamos el bucle, salvo que los números de la extrema derecha son cada vez más pequeños. Pero al cabo de miles o millones de iteraciones, la catástrofe: de pronto Z se reduce a nada, disolviéndose en una interminable secuencia de ceros.

Pueden verificarlo en el ordenador. ¿Sólo puede manejar doce dígitos? No tiene la menor importancia, pues siempre se obtiene la misma respuesta.

Los resultados de este «programa» se pueden sintetizar en tres leyes que quizá parezcan tan triviales que no vale la pena formularlas. Pero ninguna verdad matemática es trivial, y en pocos pasos estas leyes nos llevarán a un universo de prodigiosa belleza.

He aquí las tres leyes del programa «de elevación al cuadrado»:

1. Si el valor de z es igual a 1, el producto Z siempre será 1.
2. Si el valor inicial es superior a 1, el producto final tenderá a infinito.
3. Si el valor inicial es inferior a 1, el producto final tenderá a cero.

Ese círculo de radio 1 es pues una especie de mapa (o valla, si se quiere) que divide el plano en dos territorios bien demarcados. Fuera de él, los números que obedecen la ley de elevación al cuadrado tienen la libertad del infinito; los números que están dentro son prisioneros, atrapados y condenados a la extinción.

Alguien objetará: «Sólo has hablado de rangos, distancias respecto del origen. Para determinar la posición de la señal, también hay que dar su rumbo. ¿Qué hay de eso?».

Muy cierto. Afortunadamente, en este proceso de selección —esta división de las zetas en dos clases— el rumbo es irrelevante; lo mismo sucede sin importar en qué dirección apunte r. Para este sencillo ejemplo (llamémoslo conjunto C), podemos pasarlo por alto. Cuando se trata del caso más complicado del conjunto M, para el que la orientación es importante, existe un hábil truco matemático que se encarga de ello, usando números complejos o imaginarios (que en realidad no son tan complejos, y mucho menos imaginarios). Pero como no los necesitamos aquí, prometo no volver a mencionarlos.

El conjunto C se sitúa en el interior de un mapa, y su frontera es el círculo que lo delimita. Si pudiéramos examinarlo con un microscopio de infinita potencia, siempre tendría el mismo aspecto. Podríamos expandir el conjunto C hasta darle el tamaño del universo; su límite aún sería una línea de grosor cero. Pero no tiene agujeros; es una barrera impenetrable que separa eternamente las zetas de menos de 1 de las que son superiores a 1.

Ahora sí estamos preparados para vérnoslas con el conjunto M, donde estas ideas sensatas son trastocadas. Agárrense.

Durante la década de 1970, el matemático francés Benoit Mandelbrot, trabajando en Harvard e IBM, comenzó a investigar la ecuación que lo ha vuelto famoso, y que ahora escribiré en su forma dinámica:

Z 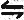z² + c

La única diferencia entre esta ecuación y la que hemos usado para describir el conjunto C es el término c. Éste, y no z, será nuestro punto de partida para trazar el mapa. En la primera vuelta del bucle, z vale cero.

Parece un cambio insignificante, pero nadie podría haber imaginado el universo que revelaría. Mandelbrot sólo obtuvo sus primeros atisbos rudimentarios en la primavera de 1980, cuando empezaron a aparecer figuras imprecisas en los gráficos del ordenador. Había comenzado a entrever las ventanas del poema de Keats:

Como veremos después, la palabra «espuma» es asombrosamente apropiada.

La nueva ecuación plantea y responde la misma pregunta que antes: ¿qué forma tiene este «territorio» cuando le insertamos números? El conjunto C era un círculo con radio 1. Veamos qué sucede cuando comenzamos con este valor en la ecuación M. Se podría hacer mentalmente… en los primeros pasos. Al cabo de varios más, ni siquiera un súper ordenador daría abasto.

Una vez puse a mi ordenador a trabajar en los términos más elevados (en el límite de mis aptitudes de programador) y generó sólo dos valores más antes de ponerse a aproximar:

En ese punto desistió, pues no cree en la existencia de números de más de 38 dígitos.

No obstante, los primeros dos o tres términos bastan para demostrar que el conjunto M debe tener una forma muy diferente del circular conjunto C. Un punto a distancia 1 está en el conjunto C; más aún, define sus límites. Un punto a esa misma distancia puede estar fuera del límite del conjunto M.

Nótese que digo «puede» y no «debe». Todo depende de la dirección inicial, o rumbo, del punto de partida, que hemos podido pasar por alto hasta ahora porque no afectaba a nuestra descripción del conjunto C, perfectamente simétrico. En cambio, el conjunto M sólo es simétrico sobre el eje horizontal X.

Podríamos haberlo deducido a partir de la naturaleza de la ecuación. Pero nadie podría haber adivinado intuitivamente su auténtica apariencia. Si me hubieran planteado la pregunta en mis días virginales anteriores a Mandelbrot, tal vez habría aventurado: «Algo parecido a una elipse, aplastada a lo largo del eje Y». Incluso podría haber llegado a la correcta conclusión (aunque lo dudo) de que estaría desplazada hacia la izquierda, la dirección del menos.

En este punto, me gustaría intentar un experimento mental. Como el conjunto M es literalmente indescriptible, he aquí mi intento de describirlo.

Imaginemos una tortuga rechoncha vista desde arriba que nada hacia el oeste. La han cruzado con un pez espada, así que tiene una punta angosta en la parte delantera. Todo su perímetro está festoneado con extravagantes criaturas marinas, y con tortuguitas de varios tamaños en las que crecen algas más pequeñas…

No hallaremos semejante definición en un texto de matemáticas. Y si alguien cree que puede superarla cuando haya visto el animal genuino, le deseo suerte. (Sospecho que el mundo de los insectos podría ofrecer analogías mejores; quizá haya un mandelescarabajo acechando en el bosque tropical brasileño. Lamentablemente, nunca lo sabremos.)

He aquí una primera aproximación simplista, despojada de detalles, como el lago Mandelbrot del castillo de Conroy (capítulo 18). Si alguien quiere llenar los espacios en blanco con esa frase típica de los cartógrafos medievales, «Aquí hay dragones», no pecará de exagerado.

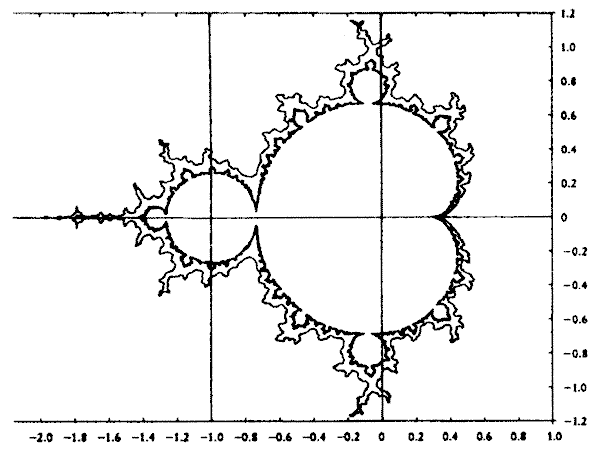
Ante todo, nótese que —como he señalado— está desplazado hacia la izquierda (el oeste, si se quiere) del conjunto C, que se extiende de +1 a –1 a lo largo del eje X. El conjunto M sólo llega a 0,25 a la derecha a lo largo del eje, aunque arriba y debajo del eje crece hasta poco más allá de 0,4.

A la izquierda, el mapa se extiende hasta alrededor de –1,4 y luego desarrolla una punta peculiar (o antena) que llega hasta exactamente –2,0. Para el conjunto M, no hay nada más allá de este punto; es la linde del universo. Los fanáticos de Mandelbrot lo llaman el «extremo oeste», y veamos lo que sucede cuando c es igual a –2. Z no converge hacia cero, pero tampoco escapa hacia el infinito, así que la punta pertenece al conjunto… por poco. Pero si damos un valor un poco mayor a c, digamos –2,00000…000001, pronto dejamos atrás Plutón y nos dirigimos hacia los cuásares.

Ahora llegamos a la distinción más importante entre los dos conjuntos. El conjunto C tiene una línea limpia como límite. La frontera del conjunto M es difusa. Empezaremos a entender cuán difusa es cuando empecemos a magnificarla; sólo entonces veremos la increíble flora y fauna que florece en ese territorio en disputa.

El límite (si así podemos llamarlo) del conjunto M no es una mera línea; es algo que Euclides nunca imaginó, y para el que no hay palabras en el lenguaje cotidiano. Mandelbrot, cuyo dominio del inglés (y del americano) es apabullante, ha saqueado el diccionario en busca de nombres sugestivos. Algunos ejemplos: espumas, esponjas, polvos, telarañas, redes, cuajados. Acuñó el término técnico «fractal», y ahora está emprendiendo una tenaz acción de retaguardia para impedir que nadie lo defina con demasiada precisión.

Los ordenadores pueden tomar «instantáneas» del conjunto M en cualquier magnificación, y son fascinantes aun en blanco y negro. Sin embargo, con un truco sencillo se pueden colorear, y transformar en objetos de una belleza asombrosa, surrealista.

La ecuación original se interesa en el color tanto como los Elementos de geometría de Euclides. Pero si pedimos al ordenador que coloree cualquier región dada según la cantidad de veces que z ejecuta el bucle antes de decidir si pertenece o no al conjunto M, los resultados son deslumbrantes.

Aunque los colores sean arbitrarios, tienen su significado. Encontramos una analogía exacta en la cartografía. Pensemos en las líneas de contorno de un mapa en relieve, que muestran la elevación sobre el nivel del mar. Los espacios entre ellas se colorean para que el ojo pueda captar mejor la información. Lo mismo vale para las cartas barométricas; cuanto más profundo sea el océano, más oscuro es el azul. El cartógrafo puede utilizar los colores que desee, y se guía no sólo por la geografía sino por la estética.

Aquí sucede lo mismo, salvo que estas líneas de contorno son fijadas automáticamente por la velocidad del cálculo. Pero no entraré en detalles. No he descubierto qué genio tuvo esta idea —quizá haya sido el mismo Monsieur M.—, pero las transforma en maravillosas obras de arte. Por no hablar de cuando se recurre a la animación…

Uno de los muchos pensamientos extraños que genera el conjunto M es el siguiente. En principio, se lo pudo descubrir en cuanto la raza humana aprendió a contar. En la práctica, como aun una imagen de baja magnificación puede implicar miles de millones de cálculos, no había modo en que se la pudiera concebir antes de que se inventaran los ordenadores. Y las películas como Nothing But Zooms de Art Matrix habrían requerido que toda la población actual del mundo realizara cálculos día y noche durante años, sin cometer un solo error en la multiplicación de billones de números de cien dígitos.

Comencé diciendo que el conjunto de Mandelbrot es el descubrimiento más extraordinario de la historia de las matemáticas. ¿Quién hubiera imaginado que una ecuación tan absurdamente sencilla podía generar una complejidad literalmente infinita, y una belleza tan cautivadora?

El conjunto de Mandelbrot es, como he tratado de explicar, esencialmente un mapa. Ya conocemos esas historias sobre mapas que revelan la posición de un tesoro escondido.