
Muchas de las especulaciones pitagóricas contenían una mezcla de misticismo y matemáticas. Pitágoras propuso dos clases diferentes de número «perfecto». El primer grupo constaba solo de un elemento: el 10. Esta cifra era perfecta por ser esencial para el sistema decimal. El argumento es, por supuesto, tautológico de pies a cabeza: si nos diese por basar nuestro sistema numérico en el 60, como los antiguos babilonios, o en el 5, como los romanos o los indios arawak sudamericanos, tales números pasarían a su vez a ser perfectos también. No obstante, Pitágoras consideraba que el 10 era perfecto porque además de lo expuesto era la suma de los cuatro primeros números:
1 + 2 + 3 + 4 = 10
Por esta razón era también conocido como tetractis y podía representarse también en forma de pirámide:

El tetractis y su representación piramidal eran sagrados para los pitagóricos, que incluso juraban por el número 10. Esta pirámide también contenía todos los números que conformaban las armonías musicales básicas: 2:1, 3:2, 4:3, por lo que estaba relacionada con la armonía de las esferas.
El segundo grupo de números «perfectos» era mucho más interesante, además de provechoso para las matemáticas. Este grupo incluía todo los números equivalentes a la suma de todos sus divisores (incluyendo el 1, pero excluyendo el propio número). Por ejemplo:
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
Los dos números perfectos siguientes son el 469 y el 8128. Estos números eran sin duda conocidos por los pitagóricos. La obra Elementos de Euclides (IX, 36) contiene una fórmula para descubrir números «perfectos» que muy bien pudo ser descubierta por los pitagóricos:
En el supuesto de que 2n – 1 sea un número primo, (2n – 1)2n–1 será un número perfecto.
Los números perfectos llevaron a Pitágoras a descubrir los números «afines». Se denominaban así las parejas de números en la que cada uno equivalía a la suma de los divisores del otro. Los números afines más bajos son 220 y 284:
220 puede dividirse entre 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110. La suma de estos divisores es 284. 284 puede dividirse entre 1, 2, 4, 71 y 142: estos números suman un total de 220.
Algunos creen ver pruebas anteriores de la existencia de los números afines en la Biblia, al hacerle Jacob una entrega simbólica de 220 granos de avena a Esaú cuando se reunieron.
Los pitagóricos también estaban al corriente del triángulo numérico:

y así sucesivamente.
Se atribuye al propio Pitágoras el descubrimiento de los tripletes pitagóricos, es decir, ternas de números que cumplen la fórmula:
a2 + b2 = c2
La fórmula para encontrar tripletes pitagóricos es la siguiente:
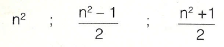
en la que n es un número impar. Este proceso era conocido por los babilonios, por lo cual cabe la posibilidad de que Pitágoras diese con él en Babilonia. No fue formulado hasta la era griega.
En el libro VI, problema 31, Euclides proporciona una prueba del teorema de Pitágoras conocida por los pitagóricos:
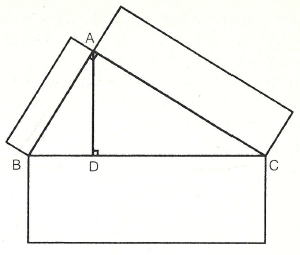
En los triángulos rectángulos, la figura lateral que subtiende al ángulo recto es igual a las figuras de forma y descripción semejantes de los lados que forman el ángulo recto.
Sea ABC un triángulo rectángulo cuyo ángulo recto está situado en BAC;
Puede decirse que la figura comprendida por BC es igual a las figuras de forma y descripción semejantes contenidas por BA y AC.
Sea AD una perpendicular trazada.
Entonces, y debido a que, en el triángulo rectángulo ABC, la perpendicular AD ha sido trazada desde el ángulo recto situado en A hasta la base BC,
Los triángulos ABD, ADC contiguos a la perpendicular son semejantes al original ABC y entre ellos (véase el libro VI, problema 8).
Y, por ser ABC similar a ABD, CB es a BA lo que AB es a BD (véase el libro VI, definición 1).
Y, por ser tres líneas proporcionales, en la medida en que la primera lo es la tercera, así la figura de la primera es semejante en forma y descripción a la de la segunda (véase el libro VI, problema 19, prisma).
Así pues, CB es a BD lo que la figura de CB es a la figura semejante en forma y descripción de BA.
Igualmente, y por la misma razón,
BC es a CD lo que la figura de BC es a la de CA; de forma que, por añadidura,
BC es a BD y a DC lo que la figura de BC es a las figuras de forma y descripción semejantes de BA y de AC.
Pero siendo BC igual a BD, DC:
La figura de BC equivale también a las figuras de forma y descripción similares de BA, AC.
Así pues, etc.
Q.E.D. [quod erat demonstrandum]
A continuación se proporciona la prueba simplificada:
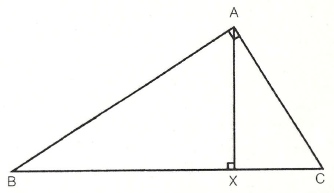
En la figura inferior, ABX + ACX = ABC, siendo estos tres triángulos semejantes, y construidos respectivamente sobre AB, AC y BC como bases. Pero las áreas de estos triángulos guardan una proporción constante con las áreas de los cuadrados de idénticas bases, así que el teorema se cumple.
En Chou pei suan ching se incluye una prueba china que data entre el 500 a. C. y el nacimiento de Cristo. Esto quiere decir que seguramente los chinos dieron por su cuenta con otra prueba.
La versión simplificada de esta prueba china es la que más belleza encierra:
Un cuadrado con lados a + b encierra un cuadrado con lados c en su interior.
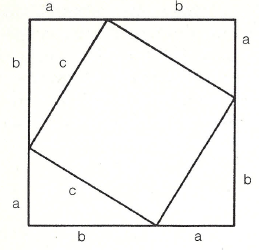
Por decirlo con sencillez, esta prueba implica equiparar el área total a las áreas del cuadrado interior y los cuatro triángulos, resultando la ecuación:
(a+b)2 = 4(1/2ab) + c2
lo cual puede simplificarse como:
a2 + b2 = c2
Hay cerca de 400 pruebas conocidas del teorema de Pitágoras, más que para cualquier otro teorema matemático. Estas pruebas han sido ideadas por gente de muy diferente condición —entre la que se incluye a un mago babilonio, un estudiante de Ohio de 14 años de edad con un nivel intelectual normal y el genio de las matemáticas de 21 años Galois, que fue muerto en un duelo. Parecida suerte corrió otro insigne autor de una prueba del teorema de Pitágoras, James A. Garfield, que se convirtió en presidente de los Estados Unidos en 1881 y fue asesinado de un tiro solo tres meses después de jurar el cargo.
Una última cosa: el escritor latino Aulo Gelio proporcionó una ingeniosa explicación de la prohibición de comer judías impuesta por Pitágoras. Según su versión, las palabras exactas de Pitágoras fueron: «¡Desgraciados, desgraciados de remate, no se os ocurra poner las manos sobre las judías!», lo cual no significaba precisamente lo que parecía. En aquellos tiempos, «judías» era utilizado para designar eufemísticamente los testículos, por lo que la prohibición de Pitágoras atañía a la actividad sexual.
Con lo que, fuese como fuese, la cuestión tenía pelotas.