

mpecé con uno de los astrónomos de la expedición, Nicholas-Antoine Nouet. Mientras que la mayoría de los franceses había maldecido el desierto por su enervante calor y las alimañas que pululaban por él, Nouet se había mostrado encantado, porque decía que aquel aire tan seco facilitaba enormemente la labor de cartografiar los cielos. «¡Es el paraíso de un astrónomo, Gage! ¡Un país sin nubes!». Lo encontré agachado en el nuevo instituto, sin chaqueta y arremangado, mientras clasificaba un juego de varillas calibradas que servía para medir las posiciones de las estrellas sobre el horizonte.
—Nouet —me dirigí a él—, ¿el cielo es constante?
El astrónomo levantó la cabeza para mirarme con irritación, dado que yo acababa de cortar el hilo de sus pensamientos.
—¿Constante?
—Quiero decir, ¿las estrellas se mueven?
—Bueno. —Nouet se enderezó y miró el jardín resguardado del sol que habían expropiado los científicos—. Nuestro planeta gira, esa es la razón por la que las estrellas parecen salir y ponerse como el sol. Forman una rueda alrededor de nuestro eje septentrional, la estrella polar.
—Pero ¿las estrellas en sí no se mueven?
—Eso aún es objeto de debate.
—Entonces hace miles de años —insistí—, cuando se construyeron las pirámides, ¿el cielo tenía el mismo aspecto que ahora?
—Ah, ya veo adonde queréis ir a parar. La respuesta es sí… y no. Las constelaciones estarían básicamente igual, pero el eje de nuestro planeta oscila de acuerdo con un ciclo de veintiséis mil años.
—El doctor Monge ya habló de eso a bordo del Orient. Dijo que la posición del zodíaco cambia con respecto al sol naciente en una fecha particular. ¿Cambiaría alguna otra cosa?
—Una diferencia que aparecería con el paso de muchos milenios sería la estrella polar. El eje terráqueo oscila, por lo que hace miles de años apuntaba hacia otra estrella del norte.
—¿Existe alguna posibilidad de que esa estrella pudiera haber sido Draco?
—Pues sí, me parece que sí. ¿Por qué lo preguntáis?
—Ya sabéis que tengo en mi poder un artefacto del pasado. Las investigaciones preliminares que he llevado a cabo aquí en El Cairo sugieren que podría representar la constelación de Draconis, el dragón. Si Draco era la estrella polar…
—Os dice que orientéis vuestro artefacto hacia el norte, quizá.
—Exactamente. Pero ¿por qué?
—Monsieur, es vuestro fragmento de antigüedad, no el mío.
—Monge me enseñó algo más en la bodega del Orient. Vi un artefacto circular en el que estaban inscritos los signos del zodíaco. Monge pensaba que era alguna clase de calendario, quizá para predecir fechas futuras.
—Eso no sería inusual entre las culturas antiguas. Los sacerdotes antiguos exhibían un gran poder si podían predecir por anticipado el aspecto que tendrían los cielos. Podían pronosticar la subida del Nilo y las fechas óptimas para la siembra y la recogida de las cosechas. El poder de las naciones y la ascensión y la caída de los reyes dependían de semejante conocimiento. Para ellos, religión y ciencia eran una sola cosa. ¿Tenéis ese artefacto? Quizá pueda ayudaros a descifrarlo.
—Lo dejamos a bordo del Orient con el tesoro maltés.
—¡Bah! ¿Para que pueda ser fundido y gastado por la próxima pandilla de bribones que consiga hacerse con el control del Directorio? ¿Por qué semejantes tesoros están a bordo de un navío de guerra que podría desaparecer en la batalla? ¡Esa es la clase de herramientas que necesitamos aquí, en Egipto! Convenced a Bonaparte de que os permita ir a buscarlo, Gage. Esas cosas son sorprendentemente simples, una vez descifradas.
Yo necesitaba algo dotado de mayor sustancia para ir a ver a nuestro general. Enoc seguía recluido en su biblioteca con el medallón cuando dos días después me enteré de que Jomard, el geógrafo al que había conocido en la bodega del Orient, iba a cruzar el Nilo hasta Gizeh para llevar a cabo las mediciones preliminares de las pirámides. Ofrecí mis servicios y los de Ashraf como guía. Talma fue también mientras que Astiza, ahora sometida a las costumbres de El Cairo, se quedaba en la casa para ayudar a Enoc.
Los cuatro disfrutamos de la brisa matinal mientras nos transportaban a través del Nilo. El río discurría cerca de las descomunales estructuras, a lo largo del promontorio de arena y piedra caliza que subía hacia la meseta donde fueron construidas. Desembarcamos e iniciamos el ascenso.
Con todo lo notable que había sido combatir a la vista de esas célebres estructuras, quedaban demasiado alejadas de Imbaba para que pudieran impresionarnos con su tamaño. Era su pureza geométrica, recortada sobre la desnudez del desierto, la que atraía la mirada. Ahora, mientras subíamos por un sendero desde el gran río, su inmensidad se volvió evidente. En un primer momento, las pirámides atisbaban por encima del borde del promontorio como deltas perfectos, su diseño tan armonioso como simple. El volumen de su masa recortada sobre el cielo elevaba la mirada hacia su ápice y nos llamaba a las alturas. Entonces, cuando se hicieron más plenamente visibles, sus titánicas dimensiones al fin fueron evidentes, montañas de piedra ordenadas por las matemáticas. ¿Cómo había construido algo tan vasto el primitivo Egipto? ¿Y por qué? El mismo aire parecía cristalino alrededor de ellas, y su majestad llevaba implícita una extraña aura, como el curioso olor acompañado de un hormigueo que siento cada vez que hago una demostración de la electricidad. Aquí todo estaba muy silencioso tras el clamor de El Cairo.
Contribuía al efecto sobrecogedor de las pirámides su célebre guardián, que miraba hacia el este. La gigantesca cabeza de piedra llamada Esfinge, tan notable como nos la habíamos imaginado a partir de las descripciones escritas, custodiaba la ladera a escasa distancia por debajo de las pirámides. Su cuello era una duna de arena y su cuerpo leonino yacía enterrado bajo el desierto. La nariz de la estatua había sido dañada hacía años por las prácticas de cañón de los mamelucos; pero su serena mirada, grandes labios africanos y tocado faraónico creaban un rostro lo bastante eterno para negar los estragos del tiempo. Sus rasgos dañados y erosionados la hacían parecer más vieja que las pirámides de más allá, e hicieron que me preguntase si no habría sido construida antes que ellas. ¿Había algo sagrado relacionado con aquel lugar? ¿Qué clase de gente había creado semejante coloso, y por qué? ¿Era un centinela? ¿Un guardián? ¿Un dios? ¿O mera vanidad para un hombre, tirano y dueño? No pude evitar pensar en Napoleón. ¿Llegaría nuestro revolucionario republicano, liberador y hombre del pueblo, a sentirse tentado alguna vez de encargar una cabeza como aquella?
Más lejos había dunas salpicadas con pilas de escombros, muros rotos y las puntas desmoronadas de pirámides de menores dimensiones. El trío de grandes pirámides que dominaba Gizeh formaba una línea diagonal, de noreste a suroeste. La Gran Pirámide de Khufu, llamada Keops por los griegos, era la más cercana a El Cairo. Una segunda, ligeramente más pequeña que venía después había sido atribuida por los griegos al faraón Khafe, o Kefrén; y una tercera aún más pequeña, al suroeste, había sido construida por un tal Menkaure.
—Uno de los detalles más interesantes de la Gran Pirámide es que está alineada precisamente con las direcciones cardinales y no sólo con el norte magnético —nos explicó Jomard mientras descansábamos unos instantes—. Es tan precisa que sus sacerdotes e ingenieros debieron tener un conocimiento muy sofisticado de la astronomía y las mediciones topográficas. Fijaos, también, en cómo se puede juzgar la dirección hacia la que uno está vuelto por la forma en que las pirámides se relacionan entre sí. El patrón de sombra funciona como una especie de brújula. Se podría usar la relación de sus ápices y sus sombras para orientar una herramienta de topógrafo.
—¿Pensáis que son una especie de hito geodésico? —pregunté.
—Eso es una teoría. Las otras dependen de la medición. Vamos. —Él y Ashraf se adelantaron, cargados con rollos de cinta métrica. Talma y yo, acalorados y sin aliento por la subida, nos quedamos un poco rezagados.
—Ni una brizna de verde —musitó Talma—. Un lugar de los muertos, desde luego.
—Pero qué tumbas, ¿eh, Antoine? —Me volví a mirar la cabeza de la Esfinge, con el río bajo nosotros y las pirámides encima.
—Sí, y tú sin tu llave mágica para entrar en su interior.
—No creo que necesite el medallón para eso. Jomard dijo que las pirámides fueron abiertas hace siglos por árabes que buscaban tesoros. Nosotros también entraremos en ellas, a su debido tiempo.
—Con todo, ¿no te molesta no tener el medallón?
Me encogí de hombros.
—Se está más fresco si no lo llevas puesto, francamente.
Talma miró los triángulos marrones que se elevaban sobre nosotros, insatisfecho.
—¿Por qué confías en esa mujer más que en mí? —El tono ofendido de su voz me sorprendió.
—Pero si no lo hago.
—Cuando te he preguntado dónde estaba el colgante, te lo has callado. Pero ella te convence de que se lo des a un viejo egipcio al que apenas conocemos.
—De que se lo preste, para que pueda estudiarlo. No se lo di a ella, se lo dejé a él. Confío en Enoc. Es un sabio, igual que nosotros.
—Pues yo no confío en ella.
—Antoine, estás celoso.
—Sí, ¿y por qué? No porque ella sea mujer, y tú vayas detrás de las hembras como un perro detrás de un hueso. No; porque no nos dice todo lo que sabe. Astiza tiene sus propios objetivos, y no son necesariamente los nuestros.
—¿Cómo lo sabes?
—Porque es una mujer.
—Una sacerdotisa, dijo ella, que intenta ayudarnos.
—Una bruja.
—Confiar en los egipcios es el único modo de llegar a resolver el misterio, Antoine.
—¿Por qué? Ellos no lo han resuelto en cinco mil años. ¿Ahora llegamos nosotros con una baratija y de pronto tenemos tantos amigos que no sabemos qué hacer con ellos? Todo esto me parece demasiado oportuno.
—Eres demasiado suspicaz.
—Y tú eres demasiado ingenuo.
Con esas palabras seguimos adelante, ninguno de los dos satisfecho.
Mientras subía por la arena resbaladiza hacia la pirámide más grande, sudando del calor, me sentí cada vez más pequeño. La mole del monumento parecía omnipresente incluso cuando le daba la espalda, un coloso que se alzaba sobre nosotros. Los despojos del tiempo dispersos sobre la arena nos rodeaban por todas partes. Dejamos atrás escombros que antaño tenían que haber sido los muros de calzadas y patios. El gran desierto se extendía más allá. Pájaros negros describían círculos en el aire dorado. Nos detuvimos ante la estructura más grande y de mayor altura del planeta, circundada por dunas que ondulaban alrededor de su base. Los bloques con los que había sido construida parecían los ladrillos de un pueblo de gigantes, inmensos y pesados.
—Y aquí quizás haya un mapa del mundo —anunció Jomard.
Con aquellas facciones tan marcadas, el sabio francés me recordaba a algunos de los halcones tallados en piedra que había visto al entrar en casa de Enoc: Horus. Ahora Jomard contemplaba la cara triangular de la pirámide con una expresión de felicidad sobrecogida.
—¿Un mapa del mundo? —preguntó Talma, escéptico.
—Eso decían Diodoro y otros estudiosos de la antigüedad. O, más bien, un mapa de su hemisferio norte.
El periodista, colorado y malhumorado por el calor, se sentó encima de un bloque puesto en posición vertical.
—Creía que el mundo era redondo.
—Lo es.
—Ya sé que vosotros los sabios sois más listos que yo, Jomard; pero a menos que esté sufriendo alucinaciones, creo que la estructura que hay ante mí termina en una punta bastante perceptible.
—Astuta observación, monsieur Talma. Tal vez vos también tengáis madera de sabio. La idea es que el ápice representa el Polo, la base el ecuador, y cada lado un cuarto de la semiesfera septentrional. Como si hubierais cortado una naranja primero por la mitad, horizontalmente, y luego en cuatro piezas verticales.
—Ninguna de ellas triángulos planos —dijo Talma, al tiempo que se abanicaba—. ¿Por qué no limitarte a construir un montículo, como una hogaza, si quieres hacer un modelo de la mitad de nuestro planeta?
—Mis mapas de Egipto y del mundo son planos y, sin embargo, representan algo redondo —contestó el sabio—. Nuestra pregunta es: ¿diseñaron los egipcios la pirámide de manera abstracta, con cierto ángulo y una determinada área, para que reflejase matemáticamente nuestro globo terráqueo? Los antiguos nos dicen que las dimensiones de la pirámide corresponden a una fracción de los 360 grados en los que dividimos el planeta. Este es un número sagrado procedente de los egipcios y los babilonios, basado en los días del año. ¿Eligieron, de hecho, determinadas proporciones para demostrar cómo había que trasladar con precisión un planeta curvo a un plano, en este caso la cara de una pirámide? Herodoto nos dice que el área de la cara de la pirámide es igual al cuadrado de su altura. Da la casualidad de que semejante proporción es una forma ideal de calcular el área de la superficie de un círculo, como nuestro planeta, a partir de un cuadrado, y de trasladar los puntos del uno al otro.
—¿Por qué harían tal cosa? —preguntó el periodista.
—Quizá para alardear de que sabían cómo hacerlo.
—Pero, Jomard —objeté yo—, la gente creyó que el mundo era plano hasta Colón.
—No, amigo mío. La luna es redonda. El sol es redondo. A los antiguos se les ocurrió que nuestro planeta también es redondo, y los griegos usaron cuidadosas mediciones para calcular la circunferencia. Mi idea es que los egipcios los precedieron.
—¿Cómo pudieron saber ellos lo grande que es nuestro planeta?
—Eso es un juego de niños si entiendes la geometría y astronomía básicas y sabes medir puntos fijos sobre la sombra del sol o la declinación de las estrellas.
—Ah, sí —dijo Talma—. Yo lo hacía antes de mis siestas cuando era un crío.
Jomard eludió la provocación.
—Cualquiera que haya visto la sombra que la tierra proyecta sobre la luna o presenciado cómo un navío desaparece bajo el horizonte sospechará que nuestro planeta es una esfera. Sabemos que el griego Eratóstenes usó las distintas longitudes de las sombras proyectadas por el sol de mediodía durante el solsticio de verano en dos lugares de Egipto, para quedarse a sólo 320 kilómetros de la respuesta correcta en el año 250 a. de C. Esta pirámide tenía casi tres mil años cuando Eratóstenes llevó a cabo sus mediciones. Sin embargo, ¿qué impediría a sus antiguos constructores hacer lo mismo, o medir la altura relativa de una estrella en los puntos norte y sur a lo largo del Nilo para calcular los ángulos y, por implicación, el tamaño de nuestro planeta? Si navegas por el cauce del río la altura de las estrellas sobre el horizonte cambia varios grados, y los marineros egipcios seguramente tuvieron que darse cuenta de ello. Si Tycho Brahe llevó a cabo tales mediciones estelares sirviéndose únicamente de sus ojos y obtuvo unos resultados lo bastante precisos para calcular el tamaño de nuestro planeta, ¿por qué no iban a poder hacerlo los antiguos? Atribuimos el nacimiento del conocimiento a los griegos, pero ellos lo atribuían a los egipcios.
Yo sabía que Jomard había leído más textos antiguos que ninguno de nosotros, así que contemplé con una nueva curiosidad la gran masa que tenía delante. El revestimiento exterior de suave piedra caliza había sido robado hacía siglos para construir palacios y mezquitas musulmanas en El Cairo, así que sólo quedaban los bloques del núcleo. Pero cada una de esas piezas era colosal, alineada en hileras que parecían no tener fin. Empecé a contar las ringleras y me di por vencido cuando iba por la número cien.
—Pero los egipcios carecían de navíos con los que dar la vuelta al globo, así que no veo por qué iban a molestarse en calcular el tamaño del planeta —objeté—. ¿Y construir una montaña para contener un cálculo? No tiene sentido.
—Tan inexplicable como edificar San Pedro para un ser que nadie salvo los santos y los lunáticos puede afirmar haber visto —confirmó Jomard—. Lo que no tiene sentido para un hombre es el propósito de su vida para otro. ¿Podemos explicarnos a nosotros mismos siquiera? Por ejemplo, ¿qué sentido tiene vuestra francmasonería, Talma?
—Bueno… —Mi amigo tuvo que pensárselo un momento antes de responder—. Vivir armoniosa y racionalmente, en vez de matarse los unos a los otros por cuestiones de religión y política, creo.
—Y henos aquí, a unos cuantos kilómetros de la carnicería que un ejército plagado de masones acaba de causar en un campo de batalla. ¿Quién puede decir quién es el lunático? ¿Quién sabe por qué los egipcios harían algo semejante?
—Yo pensaba que esto era la tumba del faraón —dijo Talma.
—Una tumba sin ocupante. Cuando los árabes buscadores de tesoros profanaron la pirámide hace siglos y cavaron túneles alrededor de bloques de granito que pretendían sellar la entrada eternamente, no encontraron nada que indicase que ningún rey, reina o siervo hubiera sido enterrado nunca dentro de ella. El sarcófago estaba vacío y le faltaba la tapa. No había ninguna escritura, y ni rastro de tesoro o bienes terrenales que conmemorasen a la persona para la que fue construida. ¡La mayor estructura del planeta, más alta que las mayores catedrales de Europa, y estaba vacía como la despensa de un campesino! Una cosa es ser megalómano, obligar a decenas de millares de hombres a que construyan tu última morada. Pero hacerlo y luego no reposar allí ya es harina de otro costal.
Miré a Ashraf, que no había podido seguir nuestra conversación en francés.
—¿Para qué sirve la pirámide? —le pregunté en mi lengua.
Ashraf se encogió de hombros, menos impresionado por el monumento que nosotros. Claro que él llevaba toda la vida en El Cairo.
—Para sostener el cielo.
Suspiré y me volví nuevamente hacia Jomard.
—¿Así que vos pensáis que es un mapa?
—Esa es una hipótesis. Otra es que sus dimensiones significan lo divino. Desde hace miles de años, los arquitectos y los ingenieros reconocen que ciertas proporciones y formas resultan más agradables a la vista que otras. Se corresponden entre sí de formas matemáticas interesantes. A algunos les parece que tan sublimes relaciones revelan verdades fundamentales y universales. Cuando nuestros antepasados construyeron las grandes catedrales góticas, intentaron usar sus dimensiones y sus proporciones geométricas para expresar ideas e ideales religiosos, con el objetivo de que el edificio pareciese sagrado por su mismo diseño. «¿Qué es Dios? —preguntó san Bernardo en una ocasión—. Dios es longitud, anchura, altura y profundidad».
Me acordé del fervor de Astiza cuando me había hablado de Pitágoras.
—¿Y? —preguntó Talma en tono retador.
—Y eso quiere decir que esta pirámide puede haber sido, para los antiguos egipcios que la construyeron, no una imagen del mundo, sino una imagen de Dios.
Contemplé con una vaga inquietud la inmensa estructura y sentí que se me erizaba el vello en la nuca. La pirámide estaba absolutamente silenciosa, pero yo podía percibir un vago zumbido de fondo salido de la nada, como el sonido de una caracola cuando te la llevas a la oreja. ¿Era Dios un número, una dimensión? Había algo de divino en la perfecta simplicidad que tenía delante.
—Por desgracia —prosiguió Jomard—, todas esas ideas son difíciles de verificar hasta que se lleven a cabo mediciones para confirmar si la altura y el perímetro se corresponden en escala con las dimensiones de nuestro planeta. Eso será imposible de hacer hasta que hayamos excavado lo suficiente para encontrar la verdadera base y las esquinas de la pirámide. Necesitaré un pequeño ejército de trabajadores árabes.
—Supongo que entonces ya podemos volver —dijo Talma esperanzadamente.
—No —dijo Jomard—. Al menos, empezaremos a medir su altura desde la hilera de piedras más baja que veamos. Gage, vos me ayudaréis con la cinta. Talma, aseguraos de escribir cada altura de un bloque de piedra que os demos.
Mi amigo miró hacia arriba desconfiadamente.
—¿Toda esa distancia?
—El sol empieza a bajar. Cuando lleguemos a la cima, hará más fresco.
Ashraf optó por quedarse abajo, claramente convencido de que sólo a unos europeos que se habían expuesto demasiado el sol se les podía ocurrir hacer semejante escalada. Y la cosa no fue nada fácil, ciertamente. La pirámide pareció mucho más empinada una vez que empezamos a subir por ella.
—Una ilusión óptica hace que parezca más baja de lo que es, cuando se la ve de frente —explicó Jomard.
—Eso no nos lo contasteis cuando iniciamos la subida —gruñó Talma.
Empleamos más de media hora de cautelosa ascensión en recorrer la mitad de la distancia. Era como escalar los bloques de construcción de unos niños titánicos, la escalera de un gigante, donde cada peldaño medía unos setenta y cinco centímetros de altura. Había una posibilidad muy real de tener una aparatosa caída. Medimos minuciosamente cada una de las hileras de piedra interiores mientras subíamos, y Talma se encargó de llevar la cuenta.
—Fijaos en el tamaño de esos monstruos —dijo el periodista—. Tienen que pesar varias toneladas. ¿Por qué no se les ocurrió construirla con piezas más pequeñas?
—¿Alguna razón de ingeniería, quizá? —sugerí yo.
—No existe ninguna necesidad arquitectónica de usar unas piedras tan grandes —dijo Jomard—. Y a pesar de ello, los egipcios cortaron estos leviatanes, los trajeron flotando sobre el Nilo, los arrastraron hasta lo alto de esa colina y, de alguna manera, luego se las arreglaron para subirlos hasta aquí arriba. Gage, vos sois nuestro experto en electricidad. ¿Pudieron emplear tan misteriosa fuerza para mover esas rocas?
—De ser así, dominaban algo que nosotros apenas entendemos. Puedo diseñar una máquina para que os haga sentir un hormigueo, Jomard, pero no para que desempeñe ningún trabajo útil. —Una vez más me sentía inadecuado para la misión que me había encomendado a mí mismo. Miré a mi alrededor en busca de algo tangible que aportar—. Aquí hay algo. Algunas de esas piedras tienen conchas incrustadas en ellas. —Las señalé.
El sabio francés siguió la dirección de mi dedo.
—¡Cierto! —exclamó con sorpresa. Se agachó para inspeccionar el bloque de caliza que le había señalado—. No son conchas, sino fósiles de conchas; como si estos bloques provinieran de debajo del mar. Es una curiosidad que ya ha sido advertida en algunas cordilleras de Europa, y ha generado un nuevo debate sobre la edad del planeta. Algunos dicen que criaturas marinas fueron transportadas hasta allí por el Diluvio Universal; pero otros afirman que nuestro mundo es mucho más antiguo de lo que indica la cronología bíblica, y que lo que hoy son montañas antes se encontraba debajo del océano.
—Si es cierto eso, las pirámides también podrían ser más antiguas que la Biblia —sugerí yo.
—Sí. Cambiar la escala del tiempo lo cambia todo. —Paseó la mirada por la piedra caliza, admirando las impresiones de conchas—. ¡Fijaos, allí! ¡Incluso tenemos un nautilo!
Talma y yo miramos por encima del hombro de Jomard. Incrustada en uno de los bloques de la pirámide había una sección transversal de la concha espiral de un nautilo, una de las formas más hermosas que existen en la naturaleza. Desde su pequeño inicio parecido a un sacacorchos sus cámaras se habían vuelto cada vez más grandes, en agradable y delicada proporción, a medida que la criatura marina crecía hacia fuera en una elegante espiral.
—¿Y en qué os hace pensar eso? —preguntó Jomard.
—En un buen plato de pescado —dijo Talma—. Tengo hambre.
Jomard ignoró el comentario y no apartó la mirada de la espiral en la roca, fascinado por alguna razón que se me escapaba. Largos minutos transcurrieron en silencio hasta que finalmente me atreví a mirar desde lo alto de nuestra atalaya. Un halcón se deslizaba por el aire a nuestra misma altura. Verlo me mareó.
—¿Jomard? —se atrevió a decir Talma pasado un buen rato—. No hace falta que vigiléis el fósil. No se va a escapar.
Como en respuesta, el sabio sacó un martillo para las rocas de la bolsa donde llevaba los instrumentos de medición y dio unos golpecitos sobre los bordes del bloque. Cerca del fósil ya había una grieta, y Jomard trabajó sobre ella hasta que consiguió desprender el espécimen de nautilo para que le cayera en la mano.
—¿Pudo ser? —murmuró, mientras le daba la vuelta a la elegante criatura para ver las pautas de luz y sombras en ella. Parecía haberse olvidado de su misión, y de nosotros.
—Aún nos falta un buen trecho para llegar a la cima —le advertí—, y pronto oscurecerá.
—Sí, sí —dijo Jomard mientras parpadeaba como si despertara de un sueño—. Dejadme pensar en esto allá arriba. —Se guardó la concha en la bolsa—. Gage, sostened la cinta. ¡Talma, preparad vuestro lápiz!
Llegar a la cima requirió otra media hora de cautelosa escalada. Nuestra medición mostró que quedaba a más de 130 metros de distancia del suelo, pero sólo conseguimos una tosca aproximación. Miré hacia abajo. Los escasos beduinos y soldados franceses que podíamos divisar parecían hormigas. Afortunadamente la piedra con la que habían rematado la pirámide ya no se encontraba allí, así que había un espacio del tamaño de una cama en el que estar de pie.
Me sentí más cerca del cielo. No había colinas que pudieran competir con la pirámide, únicamente desierto plano, la tortuosa hebra plateada del Nilo y el collar de verde sobre cada una de sus orillas. El Cairo rielaba con un millar de minaretes al otro lado del río, y podíamos oír el gemido quejumbroso que llamaba a los fieles a la plegaria. El campo de batalla de Imbaba era un coliseo cubierto de polvo, acribillado de pozos dentro de los que se arrojaba a los muertos. A lo lejos, hacia el norte, el Mediterráneo se volvía invisible sobre el horizonte.
Jomard volvió a sacar su nautilo de piedra.
—Se piensa con más claridad aquí arriba, ¿no os parece? Este templo enfoca la mente. —Se sentó en el suelo y empezó a trazar unas cuantas figuras.
—Y poca cosa más —dijo Talma, al tiempo que se sentaba con una exagerada resignación—. ¿He mencionado que tengo hambre?
Pero Jomard volvía a estar absorto en algún mundo privado y finalmente, como ya nos habíamos acostumbrado a semejantes meditaciones por parte de los sabios, permanecimos un buen rato en silencio. Yo sentía como si pudiese ver la curvatura de nuestro planeta, y me apresuré a decirme que eso era una ilusión a aquella modesta altura. Sin embargo, parecía haber una especie de foco benigno en la cima de dicha estructura, y confieso que nuestro callado aislamiento llegó a resultarme muy agradable. ¿Había estado algún otro americano allí arriba?
Finalmente Jomard se levantó del suelo sin mediar palabra, cogió un fragmento de piedra caliza tan grande como su puño y lo lanzó lo más lejos que pudo. Contemplamos la parábola de su caída, preguntándonos si habría sido capaz de arrojarla lo bastante lejos para que salvara la base de la pirámide. Pero no lo logró, ya que la piedra rebotó en los bloques de piedra de la pirámide por debajo de nosotros y se hizo añicos con el impacto. Las partículas rodaron estrepitosamente pirámide abajo.
Jomard miró ladera abajo unos instantes, como si evaluara su puntería. Luego se volvió hacia nosotros.
—¡Pues claro! Es obvio. ¡Y vuestro ojo, Gage, ha sido la clave!
—¿Lo ha sido? —pregunté con una nueva animación.
—¡Qué maravillosa es la obra sobre la que nos hallamos! ¡Menuda culminación de pensamiento, cálculo y filosofía! ¡Ha sido el nautilo lo que me ha permitido verlo!
Talma puso los ojos en blanco.
—¿Qué es lo que os ha permitido ver?
—¿Alguno de vosotros ha oído hablar de la secuencia numérica de Fibonacci?
Nuestro silencio respondió por sí solo.
—Fue introducida en Europa alrededor del año 1200 por Leonardo Pisano, también conocido como Fibonacci, después de haber estudiado en Egipto. Su verdadero origen se remonta a mucho tiempo atrás, a un pasado ignoto. Mirad. —Nos enseñó su papel. Escrita en él había una serie de números: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55—. ¿Veis la pauta?
—Me parece que una vez probé suerte con ella en la lotería —dijo Talma—. No salió ganadora.
—No, ¿veis cómo funciona? —insistió el sabio—. Cada número es la suma de los dos anteriores. El siguiente en la secuencia, sumando 34 y el 55, sería 89.
—Fascinante —dijo Talma.
—Lo asombroso que tiene esta serie es que, con geometría, puedes representar la secuencia no como números sino como una pauta geométrica. Lo haces dibujando cuadrados. —Dibujó dos pequeños cuadrados uno al lado del otro y puso un número 1 dentro de cada cuadrado—. ¿Veis?, aquí tenemos los dos primeros números de la secuencia. Ahora dibujamos un tercer cuadrado al lado de los primeros dos, haciendo que sea tan largo como los dos cuadrados sumados, y lo marcamos con el número 2. Luego dibujamos un cuadrado con los lados tan largos como un cuadrado del número 1 y un cuadrado del número 2 sumados, y lo marcamos 3. ¿Veis? —dibujaba rápidamente—. El lado del nuevo cuadrado es la suma de los lados de los dos cuadrados que lo preceden, del mismo modo que el número en una secuencia de Fibonacci es la suma de los dos números que lo preceden. Los cuadrados crecen rápidamente en área.
No tardó en crear una imagen como esta:
1,61800339
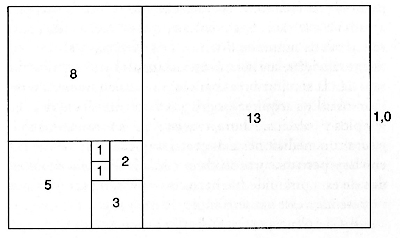
—¿Y ese número que hay arriba de todo, el 1,6 no sé cuántos, qué significa? —pregunté.
—Es la proporción de la longitud del lado de cada uno de los cuadrados respecto al cuadrado los lados que lo precede —respondió Jomard—. Fijaos en que los lados del cuadrado marcado 3 tienen una longitud proporcional con los lados del cuadrado 2 como, digamos, la proporción entre el cuadrado 8 y el cuadrado 13.
—No lo entiendo.
—¿Veis cómo la línea de arriba del cuadrado 3 queda dividida en dos longitudes desiguales por la juntura con los cuadrados 1 y 2? —dijo Jomard, con paciencia—. Esa proporción entre la longitud de la línea corta y la línea larga se repite una y otra vez, sin importar lo grande que lleguéis a hacer este diagrama. La línea más larga no tiene 1,5 veces la longitud de la corta, sino 1,618 veces, o lo que los griegos y los italianos llamaban el número áureo, o sección áurea.
Tanto Talma como yo nos erguimos ligeramente.
—¿Queréis decir que ahí hay oro?
—No, cretinos. —Jomard sacudió la cabeza con fingido disgusto, a la vez que nos miraba con un desprecio cómico—. Sólo que las proporciones parecen perfectas cuando se las aplica a la arquitectura, o a monumentos como esta pirámide. Hay algo en esa relación que es instintivamente agradable a la vista. Las catedrales fueron construidas para reflejar esos números divinos. Los pintores del Renacimiento dividían sus lienzos en rectángulos y triángulos que repetían la sección áurea para lograr una composición armoniosa. Los arquitectos griegos y romanos la usaban en templos y palacios. Ahora, tenemos que confirmar mi conjetura con mediciones más precisas que las que hemos hecho hoy, pero mi corazonada es que la inclinación de los lados de esta pirámide fue hecha así precisamente para que representara este número aúreo, 1,618.
—¿Qué tiene que ver el nautilo con todo esto?
—A eso voy. Primero, imaginaos una línea que desciende por debajo de nuestros pies desde la punta de este coloso hasta su base, para llegar al lecho rocoso del desierto.
—Puedo confirmar que es una línea muy larga, después de esa dura subida —dijo Talma.
—Más de ciento treinta metros —confirmó Jomard—. Ahora imaginaos una línea desde el centro de la pirámide hasta su borde exterior.
—Eso sería la mitad de la anchura de su base —me atreví a decir, con la sensación de ir justo dos pasos por detrás que siempre había tenido con Benjamín Franklin.
—¡Exactamente! —exclamó Jomard—. ¡Tenéis instinto para las matemáticas, Gage! Ahora, imaginad una línea que va desde ese borde exterior ladera arriba hasta donde estamos ahora, completando un triángulo recto. Mi teoría es que si se toma como punto de partida nuestra línea en la base de la pirámide, una línea hasta lo alto de la cima daría 1,618: ¡las mismas armoniosas proporciones mostradas por los cuadrados que he dibujado! —Nos miró con expresión triunfal.
Nosotros dos pusimos cara de no entender nada.
—¿No lo veis? Esta pirámide fue construida para que se ajustara a los números de Fibonacci, los cuadrados de Fibonacci, el número áureo que los pintores siempre han encontrado armonioso. ¡No es sólo que nos parezca que la encontramos perfecta, sino que realmente es perfecta!
Talma volvió la mirada hacia las otras dos grandes pirámides vecinas.
—¿Queréis decir que todas las pirámides son así?
Jomard sacudió la cabeza.
—No. Esta es especial, sospecho. Es un libro, e intenta decirnos algo. Es única por una razón que no acabo de entender.
—Lo siento, Jomard —dijo el periodista—. Me alegro de veros tan emocionado; pero el hecho de que unas líneas imaginarias igualen 1,6, o lo que quiera que habéis dicho, parece una razón todavía más ridícula para construir una pirámide que llamar a algo puntiagudo un hemisferio o construir una tumba en la que nadie será enterrado. A mí me parece perfectamente posible que si algo de todo esto es cierto, vuestros antiguos egipcios eran muy inteligentes… pero estaban bastante locos.
—Ah, es ahí donde os equivocáis, amigo mío —contestó el sabio alegremente—. Pero no os culpo por vuestro escepticismo, porque no vi lo que hemos tenido ante los ojos durante todo el día hasta que aquí Gage con su vista de lince me ayudó a encontrar el fósil de nautilo. Veréis, la secuencia de Fibonacci, traducida a geometría de Fibonacci, crea uno de los diseños más hermosos que existen en la naturaleza. Dibujemos un arco a través de estos cuadrados, desde una esquina hasta la otra, y luego unamos los arcos. —Nos enseñó el dibujo—. Entonces obtendremos una imagen como esta:
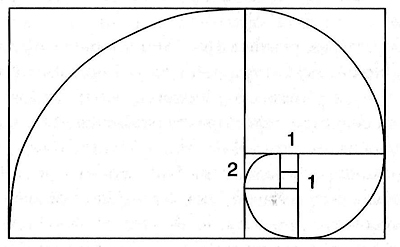
—¡Listo! ¿A qué se parece eso?
—Al nautilo —me atreví a decir. Jomard era inteligentísimo, por mucho que yo siguiera sin tener claro adonde quería ir a parar.
—¡Exactamente! Ahora imaginaos que expando esta imagen añadiendo cuadrados adicionales: 21, 34, y así sucesivamente. Esta espiral seguiría creciendo, vuelta tras vuelta, y se haría cada vez más grande y se parecería aún más a nuestro nautilo. Y esta pauta en espiral es algo que vemos una y otra vez. Cuando tomas la secuencia de Fibonacci y la aplicas a la geometría, y luego aplicas esa geometría a la naturaleza, ves que el mismo Dios utiliza esta sublime pauta numérica, esta espiral perfecta. Encontraréis la espiral en la cabeza de la semilla de una flor o en las semillas de una pina. Los pétalos de muchas flores son números de Fibonacci. Un lirio tiene 3; un ranúnculo, 5; un delfinio, 8; las caléndulas, 13; algunos áster tienen 21 y algunas margaritas, 34. No todas las plantas siguen la pauta, pero muchas de ellas lo hacen porque, además de hermosa, es la forma más eficiente de empujar semillas en crecimiento o pétalos a partir de un centro común. ¡Bien, ahora ya veis cuán maravillosa es esta pirámide! —Asintió para sí, satisfecho con su propia explicación.
—¿Es una flor? —se aventuró a preguntar Talma, con lo que me alivió de la carga de ser un poco lento de entenderás.
—No —respondió Jomard solemnemente—. Hemos escalado algo que no sólo es un mapa del mundo, monsieur periodista. Ni siquiera es sólo un retrato de Dios. De hecho es un símbolo de toda la creación, de la fuerza vital en sí misma, una representación matemática de cómo opera el universo. Esta masa de piedra incorpora no sólo lo divino, sino el mismísimo secreto de la existencia. Codifica, dentro de sus dimensiones, las verdades fundamentales de nuestro mundo. Los números de Fibonacci son naturaleza en lo que esta tiene de más eficiente y hermoso, un atisbo de la inteligencia divina. Esta pirámide los personifica y, al hacerlo, personifica la mente del mismo Dios. —Sonrió con nostalgia—. Aquí estaba toda la verdad de la vida contenida en las dimensiones de este primer gran edificio, y desde entonces todo ha sido un largo olvidar.
Talma miraba a nuestro compañero como si este se hubiera vuelto loco. Yo me quedé sentado en el suelo, sin saber qué pensar. ¿Podía la pirámide realmente existir para consagrar números? Eso parecía completamente ajeno a nuestra forma de pensar, pero quizá los antiguos egipcios vieran el mundo de otra manera. ¿También era mi medallón alguna clase de clave matemática o símbolo? ¿Guardaba alguna clase de relación con las extrañas teorías de Jomard? ¿O estaba el sabio leyendo algo en aquel montón de piedras que sus constructores nunca habían tenido intención de incluir en él?
En algún lugar por esa dirección estaba el Orient, con un calendario que quizá contuviera más claves del acertijo; y eso parecía lo siguiente que yo podía examinar. Fui a tocar el medallón escondido contra mi pecho y me llenó de una súbita inquietud el que no estuviera allí. Tal vez Talma tuviese razón: yo era demasiado ingenuo. ¿Hacía bien al confiar en Enoc? Y con el triángulo adecuado de Jomard en mente, imaginé los brazos del medallón como la varita de un zahorí que señalaba algo oculto muy por debajo de mis pies.
Bajé la vista hacia el vertiginoso camino que habíamos seguido en la subida. Ashraf caminaba por la línea de la sombra de la pirámide, con la mirada clavada en el suelo en vez de levantada hacia el cielo.