Figura 23. Entrecruzamiento de instrucciones codificadas
Máquinas que aprenden o simulan aprendizaje
Los ordenadores pueden funcionar como sistemas complejos adaptativos. Puede tratarse de equipos especialmente diseñados o bien de ordenadores convencionales programados para aprender, adaptarse o evolucionar. Hasta ahora, la mayoría de diseños o programas intentan imitar de modo simplificado el funcionamiento de algunos sistemas complejos adaptativos vivientes.
Un tipo bien conocido de sistema complejo adaptativo informático es la red neuronal, que puede implementarse tanto en forma de programa como de circuito. Constituye una tosca analogía del funcionamiento del cerebro de un mamífero (especialmente el humano). Se parte de un conjunto de múltiples nodos o unidades (que suelen llamarse neuronas, aunque no está nada claro hasta qué punto se corresponden con las neuronas individuales de un cerebro vivo). En cada instante de tiempo, cada unidad está caracterizada por un bit (0 o 1) que se supone que indica si la «neurona» se ha disparado o no. Cada unidad está conectada con algunas o todas las otras, y la influencia ejercida por una unidad sobre otra es un número positivo si la primera unidad excita a la segunda, o negativo si la inhibe. Estos coeficientes cambian a medida que progresa el aprendizaje.
Las redes neuronales pueden hacerse funcionar en ordenadores convencionales; en ese caso un programa se hace cargo de la definición de las distintas unidades y de sus efectos excitadores o inhibidores sobre las otras. Las unidades existen sólo como elementos de computación. También es posible el empleo de equipos especiales para conformar la red, que entonces se compone de unidades separadas dispuestas en paralelo.
Un ejemplo de los muchos problemas a los que las redes neuronales han sido aplicadas es aprender a leer un texto en inglés en voz alta con una pronunciación correcta. Dado que existe una notable separación entre la ortografía y la fonética inglesas, este ejercicio no es en absoluto trivial. El ordenador tiene que descubrir un número enorme de reglas generales junto con sus excepciones, que pueden considerarse reglas especiales adicionales. Si se tiene un texto lo bastante largo, tanto las reglas generales como las especiales aparecerán un número de veces suficiente como para que se comporten como regularidades. Para que la red neuronal aprenda a leer en inglés en voz alta, tiene que funcionar como un sistema complejo adaptativo. Debe hacer diversas tentativas de identificación de conjuntos de regularidades en un bloque de texto, comprimir la información obtenida en esquemas y aplicar éstos a más texto, dejando que compitan entre sí para acercarse a la pronunciación correcta, que es facilitada por un «profesor». Esta clase de aprendizaje se denomina supervisado, en oposición, por ejemplo, a la clase de aprendizaje consistente en poner a prueba los esquemas de pronunciación ante angloparlantes para ver si entienden, pero sin la presencia de un profesor que facilite la respuesta correcta. La supervisión permite definir la adaptación en términos de la diferencia entre la pronunciación correcta de un texto y la pronunciación resultante del esquema.
En la red NETtalk, tal como fue desarrollada por Terry Sejnowski y C. R. Rosenberg en 1987, los datos de entrada consistían en siete caracteres consecutivos (cada uno de los cuales podía ser una de las 26 letras del alfabeto inglés, o bien un espacio, una coma o un punto) de algún texto escrito en inglés, presentado en una ventana móvil que recorría gradualmente el pasaje. La salida era un código de pronunciación para el carácter central de los siete; este código alimentaba un generador de voz.
Los datos de entrada se identificaban con los bits correspondientes a un conjunto de 7 veces 29 (= 203) unidades, y las salidas con los bits asociados a otras 26 unidades. Había otras 80 unidades adicionales para la asistencia en el aprendizaje. Los esquemas estaban representados por tablas de coeficientes de interacción, donde las interacciones se restringían a los efectos de las unidades de entrada sobre las unidades de ayuda y los de estas últimas sobre las unidades de salida. Todos los demás coeficientes de interacción se fijaron en cero para que el proceso resultara manejable.
La red fue adiestrada por medio de los caracteres que componían un texto de 1024 palabras, acompañado del «profesor», que era la secuencia de códigos de pronunciación de todos los caracteres, la cual daba la pronunciación correcta de la totalidad del texto.
En el primer recorrido de ensayo a través del texto, los coeficientes de interacción se inicializaban en valores arbitrarios y después cambiaban (en virtud de una suerte de aprendizaje) a medida que el centro de la ventana de siete letras se desplazaba letra a letra por el texto. En cada paso, los datos de entrada y los coeficientes alimentaban una fórmula simple que daba valores de salida que indicaban opciones de pronunciación posibles. La discrepancia entre los datos de salida candidatos y los correctos se reducía después modificando los coeficientes de interacción por medio de una fórmula simple. Los coeficientes de interacción al final de la primera pasada servían de inicio para una segunda pasada sobre el mismo texto de 1024 palabras. Y así sucesivamente.
El éxito implicaba que los coeficientes, en lugar de fluctuar ampliamente de un recorrido a otro, convergerían, con sólo desviaciones mínimas, hacia valores que darían una buena aproximación de la pronunciación correcta. Las pruebas mostraron que diez pasadas de adiestramiento sobre las 1024 palabras eran suficientes para dar una pronunciación inteligible, mientras que después de cincuenta pasadas se estimó que la pronunciación era correcta en un 95 por ciento. Tras el adiestramiento, los coeficientes resultantes se emplearon para pronunciar otro bloque de texto, esta vez sin profesor. Se consiguió una pronunciación inteligible con una precisión del 75 por ciento.
Hay muchas otras versiones de redes neuronales y una plétora de problemas a los que han sido aplicadas, a menudo con un éxito considerable. El esquema se representa siempre por una tabla de coeficientes de interacción, donde cada uno representa el efecto de una unidad sobre otra. Mi colega de Caltech John Hopfield señaló en 1982 una condición que, si se impone artificialmente sobre los coeficientes de interacción, permitiría no sólo que la adaptación estuviese bien definida, sino que aumentara sin interrupción durante el proceso de aprendizaje. Se requiere que el efecto de cualquier unidad A sobre otra B sea el mismo que el de B sobre A. Esta condición es casi con toda seguridad poco realista para cerebros reales, y también es violada por muchas redes neuronales exitosas, como la misma NETtalk. Aun así, resulta instructivo el hecho de que haya situaciones en las que la adaptación está bien definida y aumenta ininterrumpidamente y otras en las que no ocurre así.
Como siempre que la adaptación está bien definida, el proceso de aprendizaje consiste en la exploración de valles sobre un relieve adaptativo. Si además la adaptación aumenta sin interrupción, de modo que la altura de la superficie explorada siempre decrece, entonces vuelve a surgir el problema de quedarse atrapado en una depresión somera cuando hay pozos profundos cerca, lo que puede paliarse introduciendo ruido. Los coeficientes de interacción podrían alterarse ligeramente de vez en cuando de forma aleatoria. Estos cambios aleatorios en el esquema recuerdan los propuestos para sacar la mente del atolladero cuando uno persigue una idea creativa. Como siempre, existe un nivel de ruido óptimo.
Puesto que las redes neuronales se inspiran en una tosca analogía con el aprendizaje en los animales superiores, uno podría preguntarse si existen también sistemas complejos adaptativos de carácter informático inspirados en una analogía con la evolución biológica. Efectivamente así es. Los primeros fueron obra de John Holland, de la Universidad de Michigan, uno de los pilares del Instituto de Santa Fe, y hacen uso de un «algoritmo genético» y un «sistema de clasificación» especial, programados en un ordenador convencional. Hasta ahora, estos sistemas han sido empleados principalmente en problemas donde la adaptación está bien definida, como el diseño de estrategias para ganar a las damas o métodos para la instalación de cableados con un costo mínimo. Sin embargo, nada impide aplicarlos a otra clase de problemas.
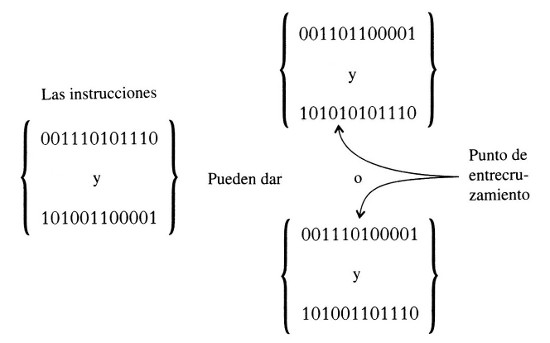
Una descripción muy simplificada del algoritmo genético sería como sigue. Cada esquema es un programa para una estrategia o método posible. Cada programa se compone de cierto número de instrucciones. La variación entre esquemas consiste en cambiar estas instrucciones, por ejemplo haciendo que entre dos de ellas se produzca un entrecruzamiento (como se muestra en la Figura 23) análogo al que tiene lugar en la reproducción sexual de los seres vivos (ilustrado en la Figura 20). Las dos instrucciones se dividen por un cierto punto en un principio y un final. El entrecruzamiento hace surgir dos nuevas instrucciones, una de ellas compuesta por el principio de la primera vieja instrucción y el final de la segunda, y la otra por el principio de la segunda y el final de la primera.

Figura 23. Entrecruzamiento de instrucciones codificadas
La modificación de un programa mediante el reemplazamiento de una o más instrucciones por otras nuevas en la forma descrita mejora unas veces la adaptación del programa y otras la empeora. Sólo poniendo a prueba los diferentes programas el computador puede juzgar la bondad de cada modificación (la realización de este tipo de juicios difíciles es lo que se conoce como «concesión de crédito»). El sistema de clasificación de John Holland proporciona una especie de mercado donde las instrucciones en competencia son compradas y vendidas. Aquéllas que acreditan un mejoramiento en la ejecución de los programas alcanzan precios más altos que las que no mejoran o empeoran la ejecución. De este modo se establece una lista ordenada de instrucciones. En esta lista entran continuamente nuevas instrucciones, a la vez que las de la cola son borradas para hacerles sitio. Las instrucciones del principio de la lista son las empleadas en los programas modificados que constituyen los esquemas mutados.
Esto es sólo un burdo bosquejo de lo que en realidad es un procedimiento bastante sofisticado. Aun así, debería quedar claro que el resultado es la evolución de los programas, y que la adaptación tiende a aumentar en el curso de dicha evolución. El bucle retroactivo que se establece entre la ejecución de un programa y la promoción o degradación de las instrucciones que lo componen no es, sin embargo, rígido, sino una tendencia general afectada por las condiciones de mercado. Esto introduce suficiente ruido en el sistema para permitir la escapatoria de las cuencas de adaptación someras y el acceso a las profundidades cercanas. Lo típico es que el sistema explore un vasto espacio de métodos o estrategias posibles y no alcance un estado estacionario —un óptimo absoluto—. La estrategia óptima para jugar al ajedrez, por ejemplo, no se ha encontrado. Si el juego en cuestión fuera en cambio el tres en raya, la máquina pronto encontraría la mejor manera de jugar y la búsqueda terminaría.
Al igual que las redes neuronales, aunque el método del algoritmo genético ha sido aplicado principalmente a problemas de búsqueda y optimización donde la adaptación (o «coyuntura») está bien definida, también puede emplearse en otros ámbitos. Tanto las redes neuronales como los algoritmos genéticos constituyen sistemas complejos adaptativos de carácter informático que pueden desarrollar estrategias nunca diseñadas por un ser humano. Es natural preguntarse si hay algo especial en estas dos técnicas, sugeridas por vagas analogías con el funcionamiento cerebral y la evolución biológica respectivamente. ¿Puede inventarse otra técnica basada en una analogía con el sistema inmunitario de los mamíferos? ¿Existe de hecho un vasto pero bien definido conjunto de sistemas complejos adaptativos de carácter informático que incluya los ya conocidos o los hipotéticos, y muchos otros más? ¿Puede describirse tal categoría superior en términos prácticos, de modo que un usuario potencial pueda buscar entre los diferentes sistemas hasta encontrar uno apropiado para su problema?
Estas cuestiones son algunas de las que intentan responder los estudiosos de los sistemas complejos adaptativos informáticos.
El empleo de ordenadores en conexión con los sistemas complejos adaptativos no se reduce ni mucho menos al desarrollo de equipos o programas destinados a la creación de sistemas complejos adaptativos informáticos encaminados a la resolución de problemas. Otra vasta área de aplicaciones informáticas es la simulación del comportamiento de los sistemas complejos adaptativos.
El rasgo más sobresaliente de tales simulaciones es la emergencia de comportamientos complejos a partir de reglas simples. Estas reglas implican regularidades de carácter general, pero los casos individuales exhiben regularidades particulares añadidas. Esta situación es similar a la de la totalidad del universo, gobernado por leyes simples que permiten una infinidad de escenarios, cada uno de los cuales exhibe sus propias regularidades, especialmente para una región del espacio y un periodo determinados, de manera que a medida que pasa el tiempo pueden emerger cada vez más formas complejas.
Para diseñar una simulación manejable el truco consiste en reducir al máximo las reglas, pero de manera que no desaparezcan los comportamientos emergentes más interesantes. El diseñador de una simulación debe, pues, saber mucho sobre los efectos de los cambios en las reglas sobre el comportamiento del sistema en escenarios muy diversos. Algunos diseñadores, como Robert Axelrod, un experto en ciencias políticas de la Universidad de Michigan, han desarrollado una aguda intuición que les permite adivinar cómo simplificar sin tirar al niño junto con el agua del baño. Naturalmente, esta intuición se basa en parte en un razonamiento a priori y en parte en la experiencia de jugar con las reglas y ver qué pasa luego. De hecho, el diseño de simulaciones simples pero ricas en consecuencias interesantes tiene más de arte que de ciencia.
¿Puede hacerse más científico el estudio de conjuntos de reglas y de sus consecuencias? Se requeriría una experiencia adicional, junto con la formulación de las intuiciones empíricas sobre qué clases de reglas conducen a qué modos de comportamiento. Después podrían conjeturarse teoremas rigurosos y por último algunos de estos teoremas podrían ser demostrados, presumiblemente por matemáticos.
De esta manera podría emerger una ciencia de las reglas y sus consecuencias, donde los experimentos serían las ejecuciones de programas y los teoremas demostrados constituirían el cuerpo de teoría. De hecho, con el advenimiento de ordenadores rápidos y poderosos se están realizando cada vez más simulaciones sencillas sobre cada vez más temas. La materia prima para la ciencia futura ya se está recopilando.
Pero en última instancia lo que de verdad importa es la relevancia de las simulaciones respecto de las situaciones reales que remedan. ¿Proporcionan las simulaciones intuiciones valiosas sobre situaciones reales? ¿Sugieren conjeturas que podrían verificarse mediante la observación? ¿Revelan posibles comportamientos antes insospechados? ¿Indican nuevas explicaciones posibles de fenómenos ya conocidos?
En la mayoría de campos las simulaciones son todavía demasiado primitivas para responder afirmativamente a estas preguntas. De todos modos, es asombroso comprobar cómo, en ciertos casos, un conjunto de reglas muy simple puede dar idea del funcionamiento de un sistema complejo adaptativo en el mundo real.
Un espléndido ejemplo es el programa TIERRA, escrito por Thomas Ray, un ecólogo de la Universidad de Delaware adscrito al Instituto de Santa Fe. Ray trabajaba en las selvas bajas de Costa Rica, en la estación de investigación biológica de La Selva. Se sintió atraído por la investigación ecológica porque quería dedicarse al estudio de la evolución. Desafortunadamente, poca evolución biológica tiene lugar en el lapso de una vida humana, lo que hizo que su campo de trabajo comenzara a parecerle frustrante. Así pues, decidió simular la evolución en un computador.
Inicialmente planeó el desarrollo de su programa en etapas, comenzando con uno supersimplificado al que se le añadirían progresivamente nuevos rasgos, como el equilibrio puntuado o la existencia de parasitismo. Tras un penoso aprendizaje autodidacta consiguió escribir y depurar un primer programa muy simple en «lenguaje máquina». Este programa inicial se llamó TIERRA, y ha resultado ser de una riqueza extraordinaria, pues Tom ha estado ocupado en el mismo desde entonces. Más aún, ciertos rasgos que él había planeado introducir más tarde, incluidos el equilibrio puntuado y el parasitismo, surgieron espontáneamente de TIERRA. El programa incluso produjo algo muy semejante al sexo.
TIERRA se vale de «organismos digitales», que son secuencias de instrucciones en código máquina que compiten por un espacio en la memoria del ordenador y por tiempo en la unidad central de proceso, de la que se sirven para su autorreplicación. En cierto sentido, la comunidad de sistemas complejos adaptativos proporcionada por TIERRA es degenerada, porque el genotipo y el fenotipo de cada organismo digital están representados por el mismo objeto, a saber, la secuencia de instrucciones. Esta secuencia es lo que experimenta mutaciones y es afectado por las presiones selectivas en el mundo real. De todas maneras, es conveniente (como ha sido remarcado por Walter Fontana) mantener una separación mental entre las dos funciones aunque ambas corran a cargo de la misma entidad. (De acuerdo con algunas teorías sobre el origen de la vida, una etapa temprana del proceso habría tenido el mismo carácter degenerado, con el ARN asumiendo el papel tanto de genotipo como de fenotipo.)
Las mutaciones se introducen de dos maneras. En primer lugar, de vez en cuando los bits cambian (de 0 a 1 o viceversa) al azar en cualquier parte del conjunto de organismos (lo que se parece mucho al modo en que los rayos cósmicos afectan a los organismos reales), a una tasa de alrededor de un bit por cada 10 000 instrucciones ejecutadas. En segundo lugar, en el curso de la replicación de los organismos digitales, los bits cambian al azar en las copias. Aquí la tasa es algo mayor, alrededor de un bit por cada 2000 instrucciones copiadas. Éstas son tasas promedio; los errores se distribuyen irregularmente en el tiempo para evitar periodicidades artificiosas.
La importancia de la muerte en biología no fue descuidada en el diseño de TIERRA. La capacidad de la memoria está severamente limitada, y en ausencia de muerte las criaturas autorreplicantes pronto la llenan, no dejando espacio para ulteriores replicaciones. De ahí el «segador», que elimina organismos regularmente según una regla que depende de la edad del organismo y de los errores cometidos por el mismo en la ejecución de ciertas instrucciones.
Tom Ray diseñó una secuencia autorreplicante de ochenta instrucciones que sirve siempre de ancestro —el organismo digital inicial— en cualquier ejecución de TIERRA. Cuando ejecutó el programa por primera vez esperaba un largo período subsiguiente de refinamiento del mismo, pero enseguida comenzaron a surgir resultados interesantes, muchos de los cuales sugerían fenómenos biológicos reales, y esta situación se ha mantenido desde entonces.
Una misteriosa novedad fue la aparición, tras un largo período de evolución, de una versión refinada del ancestro, que constaba únicamente de treinta y seis instrucciones, pero en cambio contenía un algoritmo más complejo. Cuando Tom le enseñó esta versión optimizada a un informático, éste le dijo que era un ejemplo de una conocida técnica llamada «desrizar el rizo». En TIERRA, la evolución había resuelto el problema de desrizar el rizo. Tom escribe: «La optimización es una técnica muy ingeniosa inventada por los humanos. Pero es implementada en un estilo desordenado aunque funcional que ningún humano usaría (a menos que estuviese muy borracho)».
¿De dónde salen estos organismos con un número de instrucciones distinto de ochenta? Las mutaciones no pueden producirlos directamente. Inicialmente, el sistema contiene sólo el ancestro y sus descendientes de ochenta instrucciones (que se multiplican hasta que la memoria está casi repleta, momento en que el segador comienza a trabajar; luego la población cambiante de organismos continúa ocupando casi toda la memoria). Finalmente aparecen mutaciones que alteran el genotipo de un organismo de ochenta instrucciones de un modo especial: cuando el organismo se examina a sí mismo para determinar su talla y transferirla a sus descendientes, se produce una respuesta incorrecta y se transfiere una nueva talla. De este modo, la población comienza a albergar organismos de tallas muy diferentes.
Si el primer intento de modelar la evolución biológica por este camino ha dado tantos frutos, sin duda debe haber un enorme territorio todavía por explorar. Nuevas maneras de simular cómo la evolución, operando sobre enormes períodos de tiempo, ha generado la información ahora almacenada en los organismos y las comunidades naturales de todo el mundo pueden ayudarnos no sólo a mejorar nuestra comprensión de la diversidad existente, sino a crear un clima intelectual en el que esa diversidad pueda ser mejor protegida.
El programa TIERRA, junto con otras simulaciones informáticas de la evolución biológica que puedan desarrollarse en el futuro, será especialmente valioso para que los no científicos puedan apreciar cómo funciona la evolución. A la mayoría de gente no le resulta difícil comprender, incluso sin simulaciones, cómo variaciones relativamente pequeñas combinadas con unas pocas generaciones de selección pueden producir cambios en una población. La experiencia personal con la cría de perros, periquitos, caballos o rosas puede convencer fácilmente a casi todo el mundo de la realidad de la evolución a pequeña escala. Pero la evolución a gran escala, con la aparición de nuevas especies, géneros, familias e incluso taxones superiores, es otra cosa. Hasta el relativamente cercano parentesco del elefante con el damán es duro de roer para la mayoría de gente. Todavía es más difícil visualizar la interrelación entre todas las formas de vida, incluyendo los inmensos cambios que pueden producirse en el transcurso de miles de millones de años.
Lo que para mucha gente resulta especialmente difícil de aceptar es que el azar más las presiones selectivas puedan conducir de una condición inicial simple a formas altamente complejas y a las comunidades ecológicas que las contienen. No pueden creer que tal evolución pueda tener lugar sin alguna clase de guía o designio. (Otros se resisten especialmente a la evolución de la conciencia, de la que los humanos nos sentimos tan orgullosos; creen que la conciencia no puede surgir de otra cosa que no sea una conciencia preexistente.) Dado que nunca he albergado dudas de esta clase, sólo puedo contemplarlas desde fuera. Pero para mí está claro que una manera de superarlas es dejar que la gente experimente las notables transformaciones efectuadas por millones de generaciones de procesos fundamentalmente aleatorios combinados con la selección natural. Esto sólo puede conseguirse por medio de la simulación, como en TIERRA, que puede recorrer un enorme número de generaciones en un período de tiempo razonable, y en simulaciones más sofisticadas y realistas que estarán disponibles en el futuro.
Al describir la evolución biológica en términos de azar y selección, estamos tratando los diversos procesos de mutación, por simplicidad, como si fueran puramente estocásticos. Pero de hecho podrían apartarse algo del puro azar. Varios autores citan observaciones que sugieren que las mutaciones surgen a veces de forma no aleatoria, incluso de maneras que parecen favorecer una adaptación creciente. Pero la posible existencia de efectos ocasionales de esta clase no altera la cuestión fundamental, es decir, que en ausencia de tales cambios ocasionales no aleatorios la evolución biológica procedería, hasta donde sabemos, tal como lo hace ahora.
Antes de que Tom Ray desarrollase el programa TIERRA, convoqué a un pequeño grupo de pensadores en el Instituto de Santa Fe para discutir la posibilidad de inventar un juego de ordenador que pudiera popularizarse y convenciese a los jugadores del inmenso poder del proceso evolutivo al abarcar un gran número de generaciones. Un excelente resultado del encuentro fue que, de vuelta a casa, John Holland inventó ECHO, una rica simulación por ordenador de una ecología de organismos simples. Pero la idea del juego didáctico no prosperó. Luego, al poco tiempo y de manera independiente, llegó Tom Ray con su TIERRA, que, aunque no se trata en realidad de un juego, puede en última instancia hacer la misma función.
Algunos de los participantes en el encuentro me indicaron que un bolsillo en la tapa de la primera edición del libro de Richard Dawkins El relojero ciego contenía el programa de un juego de ordenador ilustrativo de la evolución. Pero aquella clase de juego no era exactamente lo que yo tenía en mente. La cuestión es que en la evolución biológica no hay ningún diseñador en el bucle. Pero Dawkins, cuyo libro está dedicado a dejar claro este punto de una manera elegante, inventó un juego en el que el jugador introduce las presiones selectivas a medida que procede la evolución, de modo muy parecido al usuario del programa de Karl Sims para producir cuadros (el juego viene con una opción que deja a los organismos evolucionar solos, pero faltan las presiones selectivas procedentes de la comunidad ecológica a la que pertenecen). Utilizando el (sólo parcialmente justificado) lenguaje de la adaptación, se puede decir que en el juego de Dawkins la adaptación es exógena, inducida desde fuera, mientras que en la naturaleza la adaptación es endógena, determinada en última instancia, sin interferencias externas, por el carácter de la Tierra y el Sol y por sucesos aleatorios que incluyen la evolución de un enorme número de especies particulares. ¿Puede diseñarse un juego en el que los jugadores, como Tom Ray con TIERRA, aporten sólo una situación inicial y un conjunto de reglas evolutivas, y el azar y la selección natural hagan el resto?
Cualquier simulación evolutiva seria debe incluir la interacción entre poblaciones pertenecientes a numerosas especies; el medio ambiente de cada una de ellas comprende, además del entorno fisicoquímico, todos los otros organismos. Pero si lo que queremos es comprender qué ocurre con una comunidad ecológica tal en un periodo de tiempo lo bastante corto como para que los cambios evolutivos carezcan de importancia, entonces tenemos que simular un proceso ecológico.
Unos cuantos teóricos asociados al Instituto de Santa Fe han empleado modelos de ordenador para estudiar las propiedades de aquellos sistemas complejos adaptativos formados por colectivos de agentes adaptativos, los cuales elaboran esquemas para describir y predecir el comportamiento mutuo. Estos investigadores han reunido un cuerpo de conocimientos sobre dichos sistemas, que incluye tanto conjeturas plausibles como resultados demostrados para modelos particulares. El cuadro resultante es tal que la región de contenido de información algorítmica intermedio, entre el orden y el desorden, es posible que contenga un régimen que recuerda el de la criticalidad autoorganizada, ejemplificado por los montones de arena, en el cual podría haber magnitudes clave distribuidas según leyes potenciales. Y lo más importante de todo, la totalidad del sistema podría tender a evolucionar hacia la condición en que se aplican dichas leyes potenciales.
Stuart Kauffman ha llevado a cabo una buena cantidad de estudios teóricos sobre este tema, lo mismo que Per Bak. Stuart está entre quienes lo describen como «adaptación hacia el límite del caos», donde «límite del caos» se emplea aquí en un sentido algo metafórico para indicar una condición crítica entre el orden y el desorden. La expresión entera, ahora extendida en la literatura popular, fue acuñada por Norman Packard como título de un artículo sobre la aproximación a dicha condición crítica por parte de un sistema informático de aprendizaje muy simple. Por la misma época Chris Langton llevó a cabo investigaciones parecidas de forma independiente.
En los dominios ecológico y económico, donde hay aplicaciones obvias, las leyes potenciales mencionadas son bien conocidas a partir de las observaciones, en particular las que gobiernan la distribución de recursos. La conocida ley empírica de la distribución de los salarios en una economía de mercado, descubierta el siglo pasado por el economista italiano Vilfredo Pareto, se aproxima a una ley potencial para los sueldos más altos. Pareto descubrió también una ley potencial aproximada para la riqueza individual, otra vez aplicable al extremo superior del espectro.
Los ecólogos suelen fijarse en la fracción de los recursos utilizada por la totalidad de individuos de una especie dada, considerada como una función de las diversas especies de la comunidad. Aquí vuelven a aparecer las leyes potenciales empíricas. Por ejemplo, a lo largo de las costas rocosas del mar de Cortés, cerca de su extremo norte justo al sur de la orilla estadounidense, la zona intermareal contiene cierto número de organismos, como las bellotas de mar y los mejillones, que ocupan una proporción variable del área superficial de las rocas. El área total ocupada por cada especie obedece, con muy buena aproximación, a una ley potencial. Estos habitantes de las rocas son depredados por otras criaturas. Entre ellas, en lo más alto de la cadena trófica, está la estrella de mar de 22 brazos (Heliaster kubiniji). ¿Qué pasaría si se eliminase la estrella del cuadro general? De hecho esto es lo que ocurrió, a causa de alguna catástrofe, en una cierta extensión de costa, y los ecólogos pudieron observar las consecuencias. El resultado fue un reajuste del sistema formado por los organismos restantes, con nuevos valores para el área total de roca cubierta por cada especie. Sin embargo, la ley potencial aproximada todavía regía. Esto podría dar un cierto soporte empírico a la idea de que los sistemas de agentes coadaptados son atraídos hacia una especie de régimen de transición caracterizado por leyes potenciales para la distribución de recursos.
En buena parte de la investigación actual sobre los sistemas complejos adaptativos las matemáticas tienen un papel muy significativo, pero la mayoría de las veces no se trata de la clase de matemáticas que tradicionalmente predomina en la teoría científica. Supongamos que el problema consiste en la evolución temporal de un sistema tal que en cada momento su estado cambia de acuerdo con cierta ley. Muchos de los éxitos más sonados de la teoría científica se han conseguido gracias a la matemática continua, donde la variable tiempo es continua y también lo son las variables que describen el estado del sistema. Dicho estado cambia en cada momento de acuerdo con una ley expresada en términos de las variables continuas que caracterizan el sistema. En lenguaje técnico, se dice que la evolución temporal del sistema está descrita por una ecuación diferencial o un conjunto de ellas. Gran parte de los progresos en física fundamental durante los últimos siglos se fundamentan en leyes de esta clase, incluidas las ecuaciones de Maxwell para el electromagnetismo, las ecuaciones de Einstein para la gravitación en el marco de la relatividad general y la ecuación de Schrödinger para la mecánica cuántica.
Cuando estas ecuaciones se resuelven con la ayuda de un ordenador digital, lo normal es aproximar la variable continua tiempo mediante lo que se llama una variable discreta, que toma valores separados por intervalos finitos en vez de todos los valores posibles entre los instantes inicial y final que limitan el período de tiempo objeto de estudio. También las variables continuas que caracterizan el estado del sistema se aproximan mediante variables discretas. La ecuación diferencial es reemplazada por una ecuación en diferencias finitas. A medida que se reducen los intervalos entre valores contiguos de las variables discretas, tiempo incluido, la ecuación en diferencias se parece más a la ecuación diferencial que sustituye, y el ordenador digital se acerca más a la solución del problema original.
En la simulación de sistemas complejos adaptativos suele emplearse una matemática discreta semejante a la que sirve para aproximar ecuaciones diferenciales continuas en un ordenador digital, pero aquí la matemática discreta no constituye una aproximación, sino que es fundamental en sí misma. Las variables que describen el estado del sistema pueden tomar sólo algunos valores, que representan diferentes alternativas. (Por ejemplo, un organismo puede o no comerse a otro, o dos organismos pueden o no entrar en combate y, si lo hacen, puede ganar uno u otro, o un inversor puede comprar, vender o guardar acciones.)
Incluso la variable tiempo puede tomar sólo unos pocos miles de valores que representen, por ejemplo, generaciones o transacciones comerciales, según el tipo de problema. Además, en muchos problemas los cambios que experimenta el sistema en cada uno de esos instantes están determinados por una ley que depende no sólo del estado del sistema en un momento dado, sino también del resultado de un proceso estocástico.
De la clase de matemática discreta que hemos estado discutiendo suele decirse que es una matemática basada en leyes. Es una matemática natural para los ordenadores digitales, y a menudo se aplica a la simulación de sistemas complejos adaptativos compuestos por multitud de agentes individuales, cada uno de ellos un sistema complejo adaptativo a su vez. Típicamente, los agentes —como los organismos en una comunidad ecológica o los individuos y negocios en un sistema económico— desarrollan esquemas que describen el comportamiento de otros agentes y la manera de reaccionar ante él. En tales casos, la matemática basada en leyes se convierte en una matemática basada en agentes, como ocurre, por ejemplo, en el programa TIERRA.
Los ejercicios con matemáticas basadas en agentes están entre las herramientas recientes empleadas para guiar a los economistas hacia una aproximación más evolucionista. Una gran parte de la economía teórica de las últimas décadas se ha caracterizado por una preocupación por una especie de equilibrio ideal basado en mercados perfectos, información perfecta y agentes perfectamente racionales, a pesar de los esfuerzos de algunos de los mejores economistas para incorporar imperfecciones en estas tres categorías dentro de la síntesis neoclásica posterior a la segunda guerra mundial.
Según una vieja historia que circula entre los economistas, un teórico neoclásico y su educada nietecita estaban paseando por la calle en una gran ciudad norteamericana. La niña vio un billete de veinte dólares en el suelo y, como era muy formal, preguntó a su abuelo si podía cogerlo. «No, cariño», replicó él, «si fuera auténtico ya lo habría cogido alguien».
Desde hace algunos años, un puñado de estudiosos, incluidos los miembros de un grupo interdisciplinario reunido por el Instituto de Santa Fe, han dirigido sus esfuerzos hacia el estudio de las economías como sistemas complejos adaptativos en evolución, compuestos por agentes adaptativos económicos dotados de una racionalidad limitada, con información imperfecta y actuando fundamentalmente al azar y en función de la percepción de los propios intereses económicos. Las felices predicciones de la teoría del equilibrio aparecen entonces únicamente como aproximaciones, mientras que la nueva aproximación admite fluctuaciones en torno a dichas predicciones, lo que se ajusta mejor a la realidad.
En un modelo sumamente simple desarrollado por Brian Arthur. John Holland y Richard Palmer (un físico de la Universidad de Duke adscrito al Instituto de Santa Fe), los inversionistas, de una sola clase, están representados por agentes adaptativos que tratan los unos con los otros a través de una cámara de compensación. Cada acción rinde unos dividendos anuales que pueden variar de manera arbitraria. El tipo de interés anual es una constante, y la razón entre beneficio e interés determina, más o menos, el valor fundamental de la acción. Pero el precio real puede desviarse mucho del valor fundamental. Cada agente elabora esquemas elementales basados en la historia de los precios de las acciones, los cuales les dicen cuándo comprar, guardar o vender. En cualquier momento, los distintos agentes pueden estar haciendo uso de esquemas diferentes. Además, un agente dado puede tener una lista de esquemas y pasar de uno a otro según vayan las cosas. De este modo se generan fluctuaciones en los precios, a menudo exageradas y ligadas a alzas y bajas repentinas de carácter especulativo, añadidas a un valor fundamental lentamente cambiante que representa una especie de límite inferior poco definido para la desigual curva de precios en función del tiempo. Tales fluctuaciones, reminiscencias de lo que pasa en los mercados reales, surgen aquí de un modelo evolutivo que trata con agentes que distan de la perfección pero intentan mantenerse informados.
Algunos de los participantes en el movimiento para la reforma económica han demostrado que la racionalidad perfecta no sólo está en clara contradicción con los asuntos humanos, sino que es inconsistente con cualquier situación en la que se den fluctuaciones de mercado. Personalmente siempre me ha causado asombro la tendencia de tantos psicólogos, economistas y hasta antropólogos académicos a tratar a los seres humanos como entes absolutamente racionales, o casi. Mi propia experiencia, sea por introspección o por observación del comportamiento ajeno, me dice que la racionalidad es sólo uno de los muchos factores que gobiernan la conducta humana, y de ningún modo es siempre el principal. Asumir que los seres humanos son racionales a menudo facilita la construcción de teorías sobre su modo de actuación, pero tales teorías suelen ser poco realistas. Aquí, ¡ay!, reside la principal debilidad de muchas de las teorías actuales en ciencias sociales y del comportamiento. Cuando se trata de construir teorías sobre fenómenos complejos, el hacerlas más analizables puede resultar conveniente, pero no necesariamente las hace mejores a la hora de describir los fenómenos —y muy bien puede hacerlas mucho peores.
En mi opinión, la gran contribución de la teoría económica a la comprensión de los asuntos humanos es simplemente el repetido énfasis en los incentivos. En cualquier situación, ¿cuáles son los incentivos para las diferentes líneas de acción? Cuando los primeros manuscritos del mar Muerto fueron descubiertos y los despistados arqueólogos, en su afán por conseguir más trozos de pergamino, ofrecieron a los nómadas árabes una retribución fija por cada fragmento encontrado, estaban propiciando que las piezas fuesen hechas pedazos antes de ser entregadas. Los economistas estudian, a menudo de manera sofisticada, cómo actúan los incentivos en el seno de la sociedad, poniendo de manifiesto las debilidades en los sucesivos esquemas de gobierno o de gestión, análogas a las del sistema de retribución en el caso de los manuscritos del mar Muerto. Los incentivos representan presiones selectivas en el seno de un sistema económico. Aun cuando las respuestas a los mismos no sean completamente racionales, y aunque haya otras presiones en liza, los incentivos económicos contribuyen a determinar qué esquemas de comportamiento económico prevalecerán. El ingenio humano siempre se las arreglará para aprovecharse de los incentivos existentes, igual que la evolución biológica casi siempre acaba por llenar algún nicho ecológico vacante. El enfoque evolucionista de la economía, junto con el reconocimiento de la racionalidad limitada de los seres humanos, no puede sino mejorar las intuiciones de los economistas acerca de cómo operan los incentivos.
El programa económico ha sido una de las actividades más fructíferas del Instituto de Santa Fe, al estimular nuevos trabajos teóricos y modelizaciones de alta calidad. Naturalmente, como en toda ciencia teórica, el éxito debe medirse en última instancia por las explicaciones de los datos existentes y por las predicciones correctas de los resultados de futuras observaciones. El Instituto es todavía muy joven y los problemas que se estudian en él demasiado difíciles para que se obtengan éxitos espectaculares a corto plazo. Los próximos años serán críticos para juzgar la obra del Instituto, y es probable que los modelos económicos hayan dado como fruto la verificación de algunas predicciones.
Sin embargo, hay otras reformas muy necesarias en teoría económica. Algunas tentativas fueron contempladas en el plan original del programa económico del Instituto, pero todavía no se han puesto en marcha. Una cuestión vital es cómo tener en cuenta de forma apropiada valores difíciles de cuantificar.
Los economistas han sido a veces satirizados como gente que mediría el valor del amor a partir del precio de la prostitución. El valor de algunas cosas es fácil de calcular en dinero, y la tentación de tener en cuenta sólo tales cosas e ignorar todo lo demás en los cálculos de costes y beneficios es fuerte. Si se propone la construcción de una presa, un análisis clásico de costes y beneficios tendría en cuenta cosas como la energía eléctrica y el control del caudal. Por otra parte, al embalse resultante se le puede asignar un valor recreativo medido por el valor de los clubs náuticos y puertos que se construirán para acoger las embarcaciones. Es posible que en el debe del proyecto se cuente el coste de las casas que quedarán inundadas por el embalse, pero no así el valor de las plantas y animales del valle, ni el valor histórico que pueda tener el mismo, ni los lazos comunales que serán destruidos. Es difícil asignar un valor monetario a tales cosas.
La aparentemente insensible práctica de ignorar lo que es difícil de cuantificar suele atribuirse a una falta de valores. Pero en realidad es todo lo contrario, pues representa la imposición sobre cualquier análisis de un rígido sistema de valores que favorece aquellos que son fácilmente cuantificables sobre otros que son más delicados pero que, en cambio, quizá sean más importantes. Las decisiones basadas en esta manera de pensar empobrecen nuestras vidas. Muchos economistas y expertos en ciencias políticas han recomendado no considerar valores no cuantificables en el proceso político. Pero si se hace esto, todos los estudios cuantitativos, con sus cálculos precisos de lo que pasa con los valores fácilmente cuantificables, tienen que ser sopesados por quienes toman las decisiones frente a argumentos cualitativos a los que no se les puede asignar un número. Hoy día está ganando terreno la idea de consultar a la gente para comprobar qué valor asignaría a cosas como un mejoramiento de la calidad del aire, la preservación de un parque o el mantenimiento de las relaciones con el vecindario. En teoría económica, las preferencias de la gente suelen tratarse como cosas bien definidas y fijadas. Éste es un punto de vista en armonía con los ideales democráticos. Pero el destino del planeta ¿es sólo un asunto de opinión pública? ¿No tiene la ciencia algo que ofrecer?
La ciencia natural tendría que ser especialmente relevante cuando los cambios se contemplan como irreversibles o casi irreversibles. Tal como está formulada en el presente, ¿presta la economía suficiente atención a la irreversibilidad? En física, la primera ley de la termodinámica establece la conservación de la energía total, y seguir la pista de la energía en física se parece al proceso de seguir la pista del dinero en economía. Ahora bien, ¿dónde está el análogo económico de la segunda ley de la termodinámica, la tendencia de la entropía a aumentar (o no cambiar) en un sistema cerrado? La entropía sirve para definir la irreversibilidad en física, y muchos pensadores han intentado definir la noción correspondiente en economía, hasta ahora sin un éxito claro. Pero quizá la búsqueda no sea infructuosa después de todo, pues podría servir para enmendar la extendida idea de que cualquier cosa que se esté agotando puede reemplazarse por algún sustitutivo, como árboles de plástico.
Mientras tanto, los economistas más destacados han desarrollado conceptos encaminados a corregir el planteamiento de tener en cuenta sólo las cosas fácilmente convertibles en dinero. La noción de «retribución psíquica» considera el hecho de que la gente obtiene satisfacción, y por lo tanto puede sentirse pagada, con cosas intangibles, como el orgullo de ayudar a los demás. El «coste de la información» tiene en cuenta el hecho de que la gente puede no saber cómo tomar decisiones razonables en un mercado libre (por ejemplo sobre compras) si no tiene la necesaria experiencia o intuición. La «tasa social de depreciación» se supone que considera la deuda entre generaciones —el grado en que una generación determinada deprecia el futuro está relacionado con cuánto planea dejar a las generaciones que le sucederán.
Sin embargo, para los economistas que trabajan en los negocios, el gobierno y las agencias internacionales, puede que no sea fácil incluir conceptos tan avanzados en sus informes y recomendaciones. Más aún, puede ser muy difícil cuantificar algunos de estos conceptos aunque hayan sido introducidos en la teoría.
En conclusión, tanto en la teoría como en la práctica parece haber espacio para mejorar el tratamiento económico de valores difícilmente cuantificables, especialmente en casos donde estos valores están en peligro de desaparecer irreversiblemente. Los progresos que se hagan pueden ser particularmente valiosos para la preservación de la diversidad biológica y cultural.