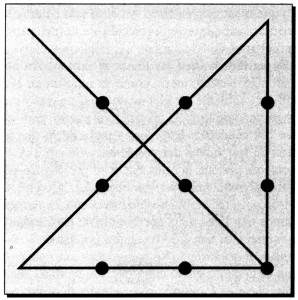
Figura 21. Solución del problema de conectar nueve puntos con cuatro líneas rectas sin levantar el lápiz del papel
Del aprendizaje al pensamiento creativo
Comenzaremos con algunas observaciones sobre la creación en el marco de la teoría científica y después exploraremos su relación con la creación en otros campos.
Cuando una nueva idea teórica se impone acostumbra a alterar y ampliar el cuerpo de teoría existente, permitiendo acomodar hechos observacionales que antes no podían comprenderse o no encajaban. También predice nuevos hechos que algún día pueden ser comprobados.
Casi siempre, la idea novedosa incluye una autocrítica negativa, el reconocimiento de que algún principio previamente aceptado es falso y debe descartarse (a menudo ocurre que una idea que era correcta en principio iba acompañada, por razones históricas, de un lastre intelectual innecesario que hay que tirar por la borda.) En cualquier caso, sólo saliéndose del marco de ideas aceptadas excesivamente restrictivas puede haber progreso.
En ocasiones, cuando una idea correcta es propuesta y aceptada por primera vez, se le da una interpretación demasiado estrecha. En cierto sentido, sus posibles implicaciones no se toman lo bastante en serio. Más adelante el autor de la idea original o algún otro teórico vuelven sobre ella para examinarla con más rigor, de modo que pueda apreciarse todo su significado.
El primer artículo de Einstein sobre la relatividad especial, que publicó en 1905 a la edad de 26 años, ilustra tanto el rechazo de una idea aceptada equivocada como la reconsideración de una idea correcta no aplicada en toda su extensión. Einstein tuvo que romper con la idea, aceptada pero errónea, de un espacio y un tiempo absolutos. Después comenzó a considerar la idea de que las simetrías presentes en las ecuaciones de Maxwell para el electromagnetismo —las simetrías correspondientes a la relatividad especial— tuviesen carácter de principio general. Hasta entonces su dominio de aplicación se había restringido al electromagnetismo, y no se pensaba que pudiesen regir, por ejemplo, en la dinámica de partículas.
A lo largo de mi carrera he tenido el placer y la fortuna de proponer unas cuantas ideas dentro del campo de la teoría de partículas elementales que, por supuesto, no me colocan a la altura de un Einstein, pero sí que han resultado ser útiles e interesantes y me han proporcionado alguna experiencia personal acerca del acto creativo en el marco de la teoría científica.
Una de mis primeras aportaciones servirá de ilustración. En 1952, cuando ingresé en la facultad de física de la Universidad de Chicago, me propuse encontrar una explicación al comportamiento de las nuevas «partículas extrañas», así llamadas porque se producían en abundancia como correspondería a una interacción fuerte, pero se desintegraban lentamente, una propiedad asociada a la interacción débil. (Aquí «lentamente» significa una vida media de alrededor de una diez mil millonésima de segundo; la tasa normal de desintegración para la interacción fuerte correspondería a una vida media de alrededor de una billonésima de billonésima de segundo, más o menos el tiempo que tarda la luz en atravesar una partícula semejante.)
Para explicar este comportamiento conjeturé la existencia de alguna ley que impidiese la desintegración inducida por la interacción fuerte, responsable de la abundante producción de partículas extrañas. La desintegración procedería entonces lentamente a través de una interacción débil. Ahora bien, ¿qué ley era ésta? Los físicos especulaban desde hace tiempo sobre la conservación en la interacción fuerte de la magnitud conocida como espín isotópico (I), que puede tomar los valores 0, 1/2, 1, 3/2, 2, 5/2, etc. Por aquellas fechas un grupo de físicos que trabajaba en el piso de abajo, bajo la batuta de Enrico Fermi, estaba comenzando a reunir pruebas experimentales en favor de esta idea, por lo que decidí comprobar si la conservación del espín isotópico podía ser la ley en cuestión.
La hipótesis convencional era que los fermiones —partículas nucleares (asociadas a la interacción fuerte) como el neutrón y el protón— deberían caracterizarse por valores de I iguales a 1/2, 3/2, 5/2, etc., siguiendo el ejemplo del neutrón y el protón, que tienen un valor I = 1/2 (la idea estaba reforzada por el hecho de que el momento angular de espín de un fermión sólo puede tomar los valores indicados). Asimismo se creía que las partículas bosónicas asociadas a la interacción fuerte, los mesones, deberían tener I = 0, 1,2, etc., como el pión, que tiene I = 1 (otra vez el paralelismo con el momento angular de espín, que para un bosón debe ser un número entero, una creencia fuertemente consolidada en el marco de la teoría entonces aceptada).
Un grupo de partículas extrañas (ahora llamadas partículas sigma y lambda) consiste en fermiones asociados a la interacción fuerte que se desintegran lentamente en un pión (I = 1) más un neutrón o un protón (I = 1/2). En un principio pensé en asignar a estas partículas extrañas un espín isotópico de 5/2, lo que impediría la desintegración inducida por la interacción fuerte. Pero esto no servía, porque efectos electromagnéticos tales como la emisión de un fotón podrían cambiar I en una unidad y burlar así la ley. En estas fui invitado por el Instituto de Estudios Avanzados de Princeton a dar una charla sobre mi idea y sus limitaciones. En la discusión sobre las partículas sigma y lambda, iba a decir «supongamos que tienen I = 5/2, de modo que la interacción fuerte no puede inducir su desintegración» para después demostrar cómo el argumento se iba a pique por culpa del electromagnetismo, al cambiar I = 5/2 por I = 3/2, un valor que permitiría a la desintegración en cuestión proceder rápidamente a través de la interacción fuerte.
Por un desliz dije «I = 1» en vez de «I = 5/2». Inmediatamente me quedé parado al darme cuenta de que eso era precisamente lo que yo andaba buscando. El electromagnetismo no puede cambiar I = 1 en I = 3/2 o I = 1/2, por lo que el comportamiento de las partículas extrañas podía explicarse por la conservación de I después de todo.
Ahora bien, ¿y la regla que afirma que los fermiones asociados a la interacción fuerte debían tener valores de I semienteros como 1/2, 3/2 o 5/2? Enseguida caí en la cuenta de que esta regla era una mera superstición, un lastre intelectual innecesario superpuesto al concepto válido de espín isotópico, y que había llegado el momento de librarse de ella. El concepto de espín isotópico veía así ampliado su dominio de aplicación.
La explicación de la desintegración de las partículas extrañas surgida de aquel lapsus linguae demostró ser correcta. Hoy día tenemos una comprensión más profunda de ella y, en correspondencia, una manera más simple de exponerla: las partículas extrañas difieren de otras más familiares como los neutrones, protones o piones en que tienen al menos un quark «extraño», o quark s, en lugar de un quark u o un quark d. Sólo la interacción débil puede transformar el «sabor» de un quark en otro, y este proceso tiene lugar lentamente.
Hacia 1970 formé parte de un pequeño grupo de físicos, biólogos, pintores y poetas reunidos en Aspen, Colorado, para debatir sobre la experiencia de la gestación de ideas creativas. Cada uno de nosotros describió un episodio referente a su propio trabajo. Yo elegí el del lapsus durante mi charla en Princeton.
Los relatos mostraban una notable concordancia. Todos habíamos encontrado una contradicción entre el modo establecido de hacer las cosas y algo que queríamos llevar a cabo: en el arte, la expresión de un sentimiento, un pensamiento, una intuición; en la teoría científica, la explicación de algunos hechos experimentales enfrentados a un «paradigma» aceptado que no permite tal explicación.
En primer lugar, habíamos trabajado durante días, semanas o meses, meditando sobre las dificultades del problema en cuestión e intentando solventarlas. En segundo lugar, había llegado un momento en que, aunque siguiéramos dándole vueltas al asunto, era inútil seguir pensando. En tercer lugar, de modo repentino, mientras paseábamos en bicicleta, nos afeitábamos o cocinábamos (o por una equivocación, como en el ejemplo descrito por mí) se presentaba la idea crucial. Habíamos conseguido salir del atolladero en que nos habíamos metido.
A todos nos llamó la atención la congruencia entre nuestras respectivas historias. Más adelante he sabido que esta percepción del acto creativo es de hecho bastante antigua. Hermann von Helmholtz, el gran fisiólogo y físico de finales del siglo pasado, describió las tres etapas de la gestación de una idea como saturación, incubación e iluminación, en perfecta concordancia con lo que los miembros del grupo de Aspen estuvimos discutiendo un siglo después.
Cabe preguntarse qué es lo que pasa durante la segunda etapa, la de incubación. Para quienes se inclinen por el psicoanálisis, una interpretación que acude de inmediato a la mente es que a lo largo del periodo de incubación, la actividad mental continúa, pero en el nivel «preconsciente», justo al borde de la conciencia. Mi propia experiencia, con el descubrimiento repentino de la solución correcta como consecuencia de un desliz, difícilmente puede ajustarse mejor a tal interpretación. Pero algunos psicólogos académicos escépticos ofrecen una hipótesis alternativa, la de que en realidad no ocurre nada durante la fase de incubación, excepto quizás un debilitamiento de la propia fe en el falso principio que entorpece la búsqueda de soluciones. El verdadero pensamiento creativo tendría lugar entonces justo antes del momento de la iluminación. En cualquier caso, entre la fase de saturación y la de iluminación siempre transcurre un intervalo de tiempo apreciable que puede considerarse como un periodo de incubación, tanto si pensamos intensamente sin ser conscientes de ello como si solamente algún prejuicio pierde gradualmente su capacidad para dificultar el hallazgo de una solución.
En 1908, Henri Poincaré añadió una cuarta etapa, importante aunque obvia: la verificación. Poincaré describe su propia experiencia en el desarrollo de una teoría para cierta clase de funciones matemáticas. Trabajó incansablemente en el problema durante dos meses sin éxito. Una noche de insomnio le pareció que «las ideas surgían en tropel; las sentía colisionar hasta que, por así decirlo, un par de ellas quedaban trabadas formando una combinación estable». Todavía no tenía la solución. Pero, un día después, estaba subiendo a un autobús que lo iba a transportar junto con varios colegas en una excursión geológica de campo cuando «… sin que nada en mis pensamientos pareciera haberle preparado el camino, me vino de pronto la idea de que las transformaciones que había empleado para definir estas funciones eran idénticas a las de la geometría no euclídea. No la verifiqué en ese momento, y cuando tomé asiento continué con una conversación iniciada antes, pero sentía una certeza absoluta. De vuelta a Caen, para tranquilizar mi conciencia, verifiqué el resultado».
El psicólogo Graham Wallas describió formalmente este proceso de cuatro etapas en 1926, y desde entonces ha sido un tema estándar dentro de la psicología aplicada, aunque pienso que ninguno de nosotros en la reunión de Aspen había oído hablar antes de él. Lo encontré por primera vez en el libro de Morton Hunt The Universe Within (El universo interior), de donde he sacado las citas anteriores.
Ahora bien, ¿es necesario pasar por un período de incubación? ¿Puede acelerarse o eludirse esta etapa de modo que no tengamos que esperar tanto para que acuda la nueva idea indispensable? ¿Podemos encontrar un atajo para salir del atolladero intelectual en el que estamos atrapados?
Hay gente que ofrece programas especiales para aprender determinadas técnicas mentales y que asegura que el pensamiento creativo puede desarrollarse con un adiestramiento adecuado. Algunas de sus sugerencias para salir del atolladero se ajustan bastante bien a una interpretación del proceso en términos de sistemas complejos adaptativos. El aprendizaje y el pensamiento en general ejemplifican el funcionamiento de los sistemas complejos adaptativos, y quizá la más alta expresión de esta facultad en la Tierra es el pensamiento creativo humano.
Como en cualquier otro análisis de sistemas complejos adaptativos, resulta instructivo introducir las nociones de adaptación y relieve adaptativo, aunque, todavía más que en el caso de la evolución biológica, no dejan de ser idealizaciones supersimplificadas. Es improbable que un conjunto de presiones selectivas sobre los procesos mentales pueda expresarse en términos de una adaptación bien definida.
Esto es especialmente cierto en la búsqueda de ideas creativas por parte de un artista. En ciencia el concepto probablemente puede aplicarse mejor: la adaptación o adecuación de una idea teórica sería una medida de hasta qué punto mejora la teoría existente, por ejemplo al explicar nuevas observaciones a la vez que mantiene o incrementa la coherencia y el poder explicativo de dicha teoría. En cualquier caso, imaginemos que tenemos un relieve adaptativo para las ideas creativas. Aquí también asociaremos una altura decreciente con una adaptación creciente (compárese con el diagrama de la Figura 19).
Como hemos visto en el caso de la evolución biológica, es demasiado simple suponer que un sistema complejo adaptativo únicamente se desliza pendiente abajo. Cuando cayese en una depresión, el sistema descendería uniformemente hasta llegar al fondo, un máximo local de adaptación. La región en forma de embudo que rodea a cada uno de estos máximos locales recibe el nombre de cuenca de atracción. Si el sistema no hiciera otra cosa que descender, está claro que sería muy probable que quedase atrapado en el fondo de una depresión poco profunda. A mayor escala hay más cuencas, algunas de las cuales pueden ser más profundas (y por lo tanto representar una mayor adaptación y ser más «deseables») que aquella en la que se encuentra el sistema, como se muestra en la Figura 19. ¿Cómo se las arregla el sistema para explorar estas otras cuencas?
Una manera de salir de una cuenca de atracción, como se discutía en el caso de la evolución biológica, tiene que ver con el ruido, entendido éste como un movimiento aleatorio superpuesto a la tendencia descendente. El ruido da al sistema la oportunidad de escapar de una depresión somera y encaminarse hacia alguna de las depresiones vecinas más profundas, hasta alcanzar el fondo de una depresión auténticamente profunda. Sin embargo, el ruido debe ser tal que las amplitudes de las excursiones aleatorias no sean demasiado grandes. De otro modo la interferencia con el proceso de descenso sería excesiva, y el sistema no permanecería en una cuenca profunda ni siquiera después de haberla alcanzado.
Otra posibilidad es que haya pausas en el proceso de descenso uniforme que permitan una exploración libre de las proximidades. Esto permitiría el descubrimiento de depresiones vecinas más profundas. Hasta cierto punto tales pausas se corresponden con el proceso de incubación en el pensamiento creativo, en el que la búsqueda metódica de la idea requerida queda en suspenso y la exploración puede continuar fuera de los límites del pensamiento consciente.
Algunas de las sugerencias para acelerar el proceso de gestación de una idea creativa se ajustan bien al cuadro del uso de un nivel controlado de ruido para evitar quedarse en el fondo de una cuenca de atracción demasiado poco profunda. Se puede intentar escapar de la cuenca original por medio de una perturbación aleatoria —Edward DeBono, por ejemplo, recomienda intentar aplicar al problema, sea cual sea, el último sustantivo de la portada del diario.
Otro método, muy empleado a lo largo de la posguerra, es el llamado «de imaginación creativa». Aquí varias personas intentan encontrar soluciones a un problema reuniéndose para una discusión colectiva en la que se anima a una de ellas a desarrollar la sugerencia de alguna otra sin que esté permitido rechazarla por muy estrafalaria que sea. Una propuesta disparatada o autocontradictoria puede representar un estado mental inestable que conduzca a una solución. DeBono gusta de citar como ejemplo una discusión sobre el control de la contaminación fluvial, en la cual alguien podría decir: «Lo que de verdad hace falta es asegurarse de que las fábricas estén aguas abajo en relación a ellas mismas». Esta sugerencia es manifiestamente imposible, pero alguien más podría derivar de ella una propuesta más seria diciendo: «Se puede hacer algo parecido a eso colocando la toma de agua de cada fábrica aguas abajo en relación al desagüe». La idea disparatada puede contemplarse como una elevación dentro del relieve adaptativo que puede conducir a una cuenca mucho más profunda que la de partida.
Edward y muchos otros han preparado material didáctico para cursos especiales de técnicas mentales para escolares, así como para empresas y hasta asociaciones de vecinos. Algunas de estas técnicas se refieren al logro de ideas creativas. Estos cursos han sido ensayados en diversas partes del mundo. En Venezuela, por ejemplo, uno de sus últimos presidentes creó un ministerio de inteligencia para fomentar la enseñanza de técnicas mentales en las escuelas de aquel país. Bajo los auspicios del nuevo ministerio un gran número de estudiantes ha seguido diversos cursos de este tipo.
Frecuentemente el contenido de los cursos destaca el uso de técnicas mentales en contextos particulares. Por ejemplo, muchos de los ejercicios de Edward tienen que ver con lo que yo llamaría análisis o estudios políticos. Se refieren a elecciones entre líneas de acción alternativas a escala de individuo, familia, organización, pueblo o ciudad, estado o provincia, nación o entidad supranacional (un ejercicio puede comenzar, por ejemplo, con la hipótesis de que una nueva ley ha sido aprobada, y seguir con una discusión sobre sus posibles consecuencias). Por regla general, los contenidos se refieren al hallazgo y análisis de argumentos a favor y en contra de diversas opciones conocidas y al descubrimiento de otras nuevas.
Una cuestión que surge de modo natural es hasta qué punto las técnicas aprendidas en un cierto contexto son transferibles a otros diferentes. Ejercitar la mente ideando nuevas opciones políticas (o sopesando los méritos relativos de las viejas) ¿sirve para descubrir ideas nuevas y aprovechables en una rama de la ciencia o para crear grandes obras de arte? ¿Sirve para que los escolares aprendan ciencias, matemáticas, historia o lengua? Es posible que algún día tengamos una respuesta clara a estas preguntas. Mientras tanto, sólo disponemos de una información muy preliminar.
Cuando alguien sigue un curso de técnicas mentales, resulta especialmente dificultoso determinar si ha tenido lugar algún progreso en la capacidad creativa del estudiante. Idealmente se debería disponer de un test más o menos normalizado, de modo que las partes interesadas —padres, funcionarios de la enseñanza y del gobierno, y legisladores— pudiesen comprobar los resultados. ¿Pero cómo puede un test normalizado medir el pensamiento creativo? Los problemas de diseño proporcionan una respuesta parcial. Por ejemplo, me han contado que en Venezuela se les pidió en una ocasión a los estudiantes de técnicas mentales que diseñaran una mesa para un pequeño apartamento. Es concebible que las respuestas a problemas de este tipo, calificadas con arreglo a un sistema de puntuación imaginativo y cuidadosamente estudiado, puedan dar alguna indicación acerca de la asimilación de las técnicas creativas por parte de los estudiantes.
David Perkins, de la Harvard Graduate School of Education, uno de los proponentes del problema de la mesa, está especialmente interesado en infundir la enseñanza de técnicas mentales a la totalidad del programa educativo y no restringirla a cursos especiales. Destaca especialmente que la necesidad de ideas creativas no surge sólo en los dominios estratosféricos de la ciencia y el arte, sino también en la vida diaria. Cita el ejemplo de un amigo que, en una excursión donde nadie había pensado en traer un cuchillo, salvó la situación cortando el queso con una tarjeta de crédito.
David señala que la investigación ha identificado cierto número de rasgos propios de la gente que, en el dominio de las ideas, consigue repetidamente salir de una cuenca de atracción para llegar a otra más profunda. Estos rasgos incluyen la dedicación a la tarea, la conciencia de estar atrapado en una cuenca inadecuada, una cierta inclinación a balancearse en las fronteras entre cuencas y la capacidad de formular y resolver problemas. Parece improbable que para poseer estos rasgos uno tenga que nacer con ellos. Es muy posible que puedan inculcarse, pero no está nada claro que las escuelas actuales hagan una labor significativa en esa dirección. Por ejemplo, como hace notar David, las escuelas son prácticamente los únicos sitios donde uno acostumbra a encontrarse con problemas ya formulados.

Figura 21. Solución del problema de conectar nueve puntos con cuatro líneas rectas sin levantar el lápiz del papel
La formulación de un problema tiene que ver con el descubrimiento de sus límites reales. Para ilustrar lo que quiero decir, tomaré prestados algunos ejemplos que mi amigo Paul MacCready, antiguo vecino y compañero de clase en Yale, suele emplear en sus conferencias como ilustración de soluciones originales a problemas (Paul es el inventor del avión a pedales, el avión de energía solar, el pterodáctilo artificial volador y otros ingenios de lo que él modestamente llama «la frontera trasera de la aerodinámica»). Aunque emplearé sus mismos ejemplos, la lección que extraeré será algo diferente.
Consideremos el famoso problema ilustrado en la Figura 21: «Conectar los nueve puntos trazando el menor número posible de líneas rectas sin levantar el lápiz del papel». Mucha gente asume que las líneas tienen que mantenerse dentro del cuadrado determinado por los puntos exteriores, aunque esta restricción no forma parte del enunciado del problema. De este modo se requieren cinco líneas para resolverlo. Si permitimos que las líneas se prolonguen por fuera del cuadrado, entonces bastan cuatro, como se muestra en la ilustración. Si este fuera un problema en el mundo real, un paso crucial en su formulación sería descubrir si hay alguna razón para confinar las líneas dentro del cuadrado. Esto forma parte de lo que yo llamo la determinación de los límites del problema.
Si el problema permite que las líneas se prolonguen por fuera del cuadrado, quizá permita también otras libertades. ¿Qué tal si rompemos el papel en trozos, lo redistribuimos de modo que los puntos queden en fila y dibujamos una línea recta por encima de ellos en un solo trazo? Varias ideas como ésta han sido recogidas por James L. Adams en su libro Conceptual Blockbusters (Rompecabezas conceptuales). La mejor estaba en una carta que le envió una jovencita, reproducida en la Figura 22. El punto clave es la última frase: «Nadie dijo que no se pudiera usar una línea gruesa». ¿Están prohibidas las líneas gruesas o no? ¿Cuáles son las reglas en el mundo real?

Figura 22. Carta de una niña de diez años dirigida al profesor Adams. (De Conceptual Blockbusting. A guide to Better Ideas, de James L. Adams, tercera edición, Addison-Wesley, Reading, Mass., pág. 31. Copyright 1974, 1976, 1979, 1986 by James L. Adams. Reproducido con autorización)
Como siempre, determinar los límites del problema es un tema fundamental en la formulación del mismo. Este punto se pone de manifiesto de manera aún más clara en «La historia del barómetro»[2], escrita por un profesor de física, el doctor Alexander Calandra de la Universidad de Washington en St. Louis:
Hace algún tiempo recibí una llamada de un colega para preguntarme si quería hacer de árbitro en la calificación de una pregunta de examen. Por lo visto a un estudiante se le había puesto un cero por su respuesta a una cuestión de física, mientras que él reclamaba que merecía la nota máxima y que se la habrían dado si no fuera porque el sistema siempre va en contra del alumno. Estudiante y profesor acordaron someter el asunto a un árbitro imparcial, y yo había sido el elegido…
Fui al despacho de mi colega y leí la pregunta en cuestión, que decía así: «Mostrar cómo se puede determinar la altura de un edificio elevado con la ayuda de un barómetro».
La respuesta del estudiante era: «Se toma el barómetro en lo alto del edificio, se le ata una cuerda larga, se baja el barómetro hasta el suelo y después se vuelve a subir midiendo la longitud de cuerda que hubo que soltar. Esta longitud es la altura del edificio».
Era una respuesta en verdad interesante, pero ¿había que aprobar a su autor? Por mi parte señalé que el estudiante merecía sin duda la nota máxima, pues había contestado la cuestión completa y correctamente. Por otro lado, si se le daba la nota máxima, esto podía contribuir a que el estudiante aprobara el curso de física. Un aprobado se supone que certifica que el estudiante sabe algo de física, pero la respuesta a la pregunta no lo confirmaba. Con esto en mente, sugerí darle al estudiante otra oportunidad para responder la cuestión. No me sorprendió que mi colega profesor estuviera de acuerdo, pero sí que lo estuviera también el alumno.
En virtud del acuerdo, le concedí al estudiante seis minutos para responder, con la advertencia de que la respuesta debería denotar algún conocimiento de física. Al cabo de cinco minutos todavía no había escrito nada. Le pregunté si quería dejarlo, pues tenía que hacerme cargo de otra clase, pero dijo que no, que tenía muchas respuestas en mente, sólo estaba pensando cuál era la mejor. Me disculpé por interrumpirle y le rogué que continuara. En el minuto que quedaba escribió rápidamente la respuesta, que era ésta: «Se toma el barómetro en lo alto del edificio y se apoya en el borde del techo. Se deja caer, midiendo lo que tarda en llegar al suelo con un cronómetro. Después, empleando la fórmula S = 1/2gt2 [distancia recorrida en la caída igual a una mitad de la aceleración de la gravedad por el tiempo transcurrido al cuadrado], se calcula la altura del edificio».
En este punto pregunté a mi colega si se daba por vencido. Él asintió y le puse al estudiante un notable. Cuando mi colega se fue, recordé que el estudiante había dicho que tenía otras respuestas al problema y le pregunté cuáles eran. «Oh, sí», dijo él. «Hay muchas maneras de averiguar la altura de un edificio grande con la ayuda de un barómetro. Por ejemplo, se puede coger el barómetro en un día soleado, medir la altura del barómetro y la longitud de su sombra y después la longitud de la sombra del edificio, y por medio de una proporción simple se determina la altura del edificio».
«Muy bien», dije. «¿Y las otras?»
«Sí», dijo el estudiante. «Hay una medición muy básica que le gustará. Se coge el barómetro y se comienza a subir las escaleras. A medida que se sube, se marca la longitud del barómetro y esto nos dará la altura del edificio en unidades barométricas. Un método muy directo.
»Naturalmente, si prefiere un método más sofisticado, puede atar el barómetro al final de una cuerda, hacerlo oscilar como un péndulo y determinar el valor de g [la aceleración de la gravedad] a la altura de la calle y en lo alto del edificio. A partir de la diferencia entre los dos valores de g se puede calcular en principio la altura del edificio.»
Finalmente, concluyó: «Si no me tuviera que limitar a las soluciones físicas del problema, hay muchas otras, como por ejemplo coger el barómetro por la base y golpear en la puerta del portero. Cuando éste conteste, se le dice lo siguiente:
»Querido señor portero, aquí tengo un barómetro de muy buena calidad. Si me dice la altura de este edificio, se lo regalo…»