Figura 11. Ejes de polarización usados en criptografía cuántica
Mecánica cuántica y verborrea
Aunque muchas cuestiones sobre la mecánica cuántica todavía no tienen una respuesta satisfactoria, no hay necesidad de introducir mistificaciones innecesarias donde de hecho no existe ningún problema. Sin embargo, esto es lo que se ha hecho en un gran número de escritos recientes sobre mecánica cuántica.
Como esta disciplina sólo predice probabilidades, en algunos círculos se piensa que la mecánica cuántica permite que ocurra prácticamente cualquier cosa. ¿Es eso cierto? Todo depende de si se toman en consideración sucesos de una probabilidad pequeñísima. Recuerdo que cuando era estudiante me propusieron el problema de calcular la probabilidad de que un objeto macroscópico masivo se elevase un metro en el aire durante un cierto tiempo como consecuencia de una fluctuación cuántica. La respuesta era, aproximadamente, uno dividido por un número con sesenta y dos ceros. La finalidad del problema era enseñamos que en la práctica no hay diferencia entre una probabilidad así y cero. Algo tan improbable resulta, de hecho, imposible.
Cuando nos fijamos en las cosas que pueden pasar en la realidad con una probabilidad significativa, encontramos que muchos fenómenos que resultaban imposibles en el marco de la física clásica continúan siéndolo en el universo cuántico. Sin embargo, la comprensión de esto por parte del público se ha visto dificultada en los últimos años por una fiebre de libros y artículos con referencias equívocas a ciertos elegantes desarrollos teóricos obra de John Bell y a los resultados de un experimento relacionado con ellos. Algunas de las referencias a este experimento, que implica dos fotones que se mueven en direcciones opuestas, han dado a los lectores la falsa impresión de que la medida de las propiedades de uno de los fotones afecta instantáneamente las del otro. La conclusión que se extrae es que la mecánica cuántica permite la comunicación a mayor velocidad que la luz. ¡Incluso se ha llegado a decir que hace plausibles fenómenos «paranormales» como la precognición! ¿Cómo se ha llegado a esta situación?
En cierto modo, la historia parte de la actitud de Einstein hacia la mecánica cuántica. Aunque colaboró en la preparación del camino que conduciría hasta ella a principios de siglo con su brillante trabajo sobre los fotones, en el que por primera vez tomó en consideración la hipótesis cuántica original de Max Planck, a Einstein nunca le gustó la mecánica cuántica en sí misma. En la Conferencia Solvay de 1930 en Bruselas, Einstein presentó lo que pretendía ser una demostración de la inconsistencia de la mecánica cuántica. Niels Bohr y sus aliados trabajaron frenéticamente en los días siguientes para encontrar el fallo en el argumento de aquel gran hombre. Antes del fin de las sesiones, pudieron demostrar que Einstein había omitido algo; curiosamente, su olvido había sido precisamente la relatividad general. Cuando concluyó la conferencia, la alegada inconsistencia había desaparecido.
Después de aquello, Einstein abandonó sus intentos de probar que la mecánica cuántica era internamente inconsistente. En lugar de eso, se concentró en identificar el principio que esta disciplina violaba y que, según él creía, debía obedecer cualquier marco teórico correcto. En 1935, junto con dos jóvenes colaboradores, Podolsky y Rosen, publicó un artículo en el que describía dicho principio y un experimento hipotético en el que la mecánica cuántica dejaría de satisfacerlo. El principio, que él llamó «de completitud», desafiaba la naturaleza esencial de la mecánica cuántica.
Podemos describir el principio de completitud como sigue: si por medio de cierta medida podemos predecir con certidumbre el valor de una cierta magnitud Q, y si por medio de otra medida alternativa y diferente podemos estimar con certeza el valor de la magnitud R, entonces, de acuerdo con la noción de completitud, debería ser posible asignar valores simultáneos exactos a ambas magnitudes Q y R. Einstein y sus colegas aplicaron el principio a dos cantidades que en mecánica cuántica no pueden medirse simultáneamente con precisión, a saber, el momento y la posición de un mismo objeto. Se establecía así una contradicción entre la mecánica cuántica y el principio de completitud. ¿Cuál es la relación real, dentro del marco de la mecánica cuántica, entre una medida que permite establecer el valor exacto de la posición de una partícula en un instante determinado y otra medida que permite obtener el valor del momento en el mismo instante? Esas medidas tienen lugar en dos ramas diferentes, decoherentes entre sí (como una rama histórica en la que un caballo gana la carrera y otra en la que gana un caballo distinto). La exigencia de Einstein equivale a aceptar que los resultados de dos ramas alternativas deben aceptarse simultáneamente. Y eso implica claramente abandonar la mecánica cuántica.
Einstein quería en realidad reemplazar la mecánica cuántica por un marco teórico diferente. En comentarios hechos aquí y allá, manifestó su creencia en que el éxito de la mecánica cuántica tenía sus raíces en resultados teóricos que sólo aproximadamente eran correctos, y que representaban una especie de promedio estadístico sobre las predicciones de otra clase de teoría.
Esta concepción einsteniana asumió una forma más definida cuando diversos teóricos, en diferentes momentos, sugirieron que había que sustituir la mecánica cuántica por una teoría clásica y determinista —pero en la que hay presente un gran número de «variables ocultas»—. Estas variables pueden imaginarse como si describiesen un enjambre de moscas invisibles zumbando por todas partes en el universo más o menos al azar, interactuando con las partículas elementales y afectando su comportamiento. Puesto que estas moscas son indetectables, lo mejor que puede hacer un físico teórico a la hora de realizar predicciones es tomar un promedio estadístico sobre sus movimientos. Pero estas moscas invisibles generan fluctuaciones imprevisibles, creando así indeterminaciones. La esperanza era que estas indeterminaciones encajasen de alguna manera con las de la mecánica cuántica, de modo que las predicciones del nuevo esquema concordaran con las predicciones mecanocuánticas en todos los casos en que la experiencia confirmaba éstas últimas.
Conocí a un físico teórico que estuvo vacilando, al menos por un tiempo, entre la aceptación de la mecánica cuántica y la idea de que podría ser sustituida por alguna teoría de «variables ocultas». Era David Bohm, quien durante toda su carrera profesional se preocupó de comprender el significado de la mecánica cuántica.
En 1953, cuando acababa de doctorarse y era un estudiante postdoctoral en el Instituto de Estudios Avanzados, David trabajaba como profesor asistente en la Universidad de Princeton. Los dos estábamos solteros y a veces pasábamos la tarde paseando por los alrededores de Princeton, discutiendo de física. David me confesó que, como marxista que era, le costaba aceptar la mecánica cuántica (el marxismo tiende a preferir teorías completamente deterministas). Dado que la mecánica cuántica tenía un éxito arrollador, no contradicho por ninguna experiencia, había intentado convencerse a sí mismo de que esta teoría era, después de todo, filosóficamente aceptable. En su intento de reconciliar la mecánica cuántica con sus convicciones marxistas, había escrito un manual elemental sobre teoría cuántica, poniendo especial énfasis en su interpretación. El libro estaba a punto de publicarse, y David estaba ansioso por mostrar a Einstein los capítulos más relevantes y ver si podía así vencer las objeciones de aquel gran hombre. Me pidió que le concertase una cita. Le respondí que yo no era la persona más indicada, pues apenas le conocía, pero que hablaría con la señorita Dukas, la formidable secretaria de Einstein, para ver qué se podía hacer.
Cuando me encontré a David uno o dos días más tarde y me disponía a decirle que estaba preparando su cita, me interrumpió entusiasmado para anunciarme que ya no era necesaria. Su libro había salido a la venta y Einstein ya lo había leído y le había telefoneado para decirle que la suya era la mejor presentación del caso en su contra que jamás había visto, y que estaría encantado de encontrarse con él para discutirla. Naturalmente, cuando vi a David al día siguiente, me moría por saber cómo se había desarrollado la conversación, y así se lo pregunté. David me miró un tanto avergonzado y me dijo: «Me ha disuadido de todo. Estoy de nuevo donde estaba antes de escribir el libro». Desde entonces, y durante más de cuarenta años, David intentó reformular y reinterpretar la mecánica cuántica para superar sus dudas. Hace muy poco me enteré, con gran pesar, de que había muerto.
Hace muchos años, David Bohm propuso sustituir el hipotético experimento de «completitud» de Einstein, Podolsky y Rosen (que no hace falta describir aquí) por una versión modificada, más práctica. El experimento de Bohm (llamado EPRB en honor a los cuatro físicos) implica la desintegración de una partícula en dos fotones. Si la partícula está inicialmente en reposo y no tiene «espín» intrínseco, los dos fotones producidos viajan en direcciones opuestas, poseen la misma masa y tienen idéntica polarización. Si uno de los fotones tiene una polarización circular levógira (es decir, «gira» hacia la izquierda), el otro está en el mismo estado, y lo mismo ocurre con la polarización dextrógira. Si uno está polarizado linealmente (es decir, su campo eléctrico oscila según un cierto eje) entonces también lo está el otro.
Se asume que todo está dispuesto de manera que nada perturba a los fotones hasta que penetran en un detector. Si se mide la polarización circular de uno de los fotones, se conoce también la polarización del otro —es la misma—. Análogamente, si se mide el plano de polarización de un fotón, se conoce igualmente el del otro —de nuevo el mismo—. La condición de completitud de Einstein implicaría que se puede asociar un valor definido a la polarización plana o circular del segundo fotón. Pero no se puede determinar simultáneamente la polarización plana y la polarización circular de un fotón (no más que la posición y el momento de una partícula). En consecuencia, el requerimiento de completitud tampoco es razonable en este caso desde el punto de vista de la mecánica cuántica. Las dos medidas, una de la polarización plana y otra de la circular, son alternativas; tienen lugar en ramas diferentes de la historia y no hay razón para considerar los resultados de ambas a la vez.
Más tarde, los trabajos de John Bell demostraron que el experimento EPRB podía emplearse para distinguir la mecánica cuántica de las hipotéticas teorías de variables ocultas, a través de ciertas medidas de la polarización de ambos fotones. El teorema de Bell (también conocido como desigualdades de Bell) se refiere a una magnitud particular que especifica la correlación entre las polarizaciones de ambos fotones. En mecánica cuántica, esta cantidad puede tomar valores no permitidos en una teoría clásica de variables ocultas.
Tras la publicación de la obra de Bell, varios equipos de físicos experimentales realizaron el experimento EPRB. Los resultados fueron esperados con ansiedad, pese a que virtualmente todos los físicos apostaban por la corrección de la mecánica cuántica; las experiencias acabaron dándoles la razón. Uno podría haber esperado que la gente de todo el mundo interesada en el tema soltase un suspiro de alivio al oír las noticias, para luego seguir con su vida normal. En vez de eso, empezó a propagarse una ola de artículos alegando que la mecánica cuántica había demostrado tener propiedades fantásticas e inquietantes. Por supuesto, se trataba de la misma mecánica cuántica de siempre. No había nada nuevo, salvo su confirmación y la subsiguiente verborrea desbordada.
La principal distorsión diseminada por los medios de comunicación y por varios libros fue la implicación, incluso la afirmación taxativa, de que el medir la polarización, plana o circular, de uno de los fotones afectaba de alguna manera al otro fotón. En realidad, la medida no causa la propagación de ningún efecto físico de un fotón al otro. ¿Qué es lo que ocurre entonces? Si, sobre una particular rama de la historia, se mide la polarización plana de uno de los fotones y se especifica así con certeza, entonces, sobre la misma rama de la historia, la polarización plana del otro fotón queda igualmente especificada con total certidumbre. En una rama diferente de la historia puede especificarse la polarización circular de uno de los fotones, en cuyo caso queda especificada con certeza la polarización circular de ambos fotones. En cada rama la situación es similar a la de los calcetines de Bertlmann, descrita por John Bell en uno de sus artículos. Bertlmann es un matemático que siempre lleva un calcetín de color rosa y otro de color verde. Si se le mira un pie y se ve un calcetín verde, se sabe inmediatamente que en el otro pie lleva uno rosa. Y, sin embargo, no se ha propagado ninguna señal de un pie al otro. Tampoco viaja ninguna señal de un fotón a otro en el experimento que confirma la mecánica cuántica. No se produce ninguna acción a distancia.
La falsa afirmación de que la medida de uno de los fotones afecta instantáneamente al otro conduce a toda clase de conclusiones desafortunadas. En primer lugar, el efecto alegado, al ser instantáneo, viola el requerimiento de la teoría de la relatividad de que ninguna señal —ningún efecto físico— puede viajar a una velocidad mayor que la de la luz. Si una señal pudiese viajar a una velocidad superior, habría observadores en determinados estados de movimiento que la verían propagándose hacia atrás en el tiempo. De aquí el ripio:
Había una señorita llamada Resplandor
Que podía viajar más deprisa que la luz.
Un día partió por una ruta relativa,
Y regresó a casa la noche anterior
Después, ciertos escritores han afirmado que la mecánica cuántica podría dar cabida a fenómenos «paranormales» como la precognición, en que se supone que individuos «psíquicos» pueden conocer de antemano el resultado de procesos aleatorios. Es innecesario decir que estos supuestos fenómenos resultan tan molestos para la mecánica cuántica como para la física clásica; si resultaran ser verdaderos, su explicación requeriría una total reformulación de las leyes de la naturaleza tal como las conocemos ahora.
Otro producto de la verborrea es la presentación de propuestas, dirigidas por ejemplo al Departamento de Defensa de los Estados Unidos, para aplicar la mecánica cuántica al diseño de sistemas de comunicación militares más rápidos que la luz. Uno se pregunta si el advenimiento de esta nueva categoría de proyectos estrafalarios no representará el declive de otros más antiguos, como la antigravedad o el movimiento perpetuo. Si no es así, la burocracia que se encarga de ellos deberá emplear más personal.
Mientras tanto, investigadores serios han comenzado a pensar en las posibles aplicaciones del efecto EPRB. En lugar de ideas estrafalarias, se están considerando aplicaciones potenciales fascinantes. Por ejemplo, Charlie Bennett, Gilíes Brassard y Arthur Ekert han estado desarrollando una forma de criptografía cuántica en la que el efecto EPRB se emplea reiteradamente para generar una cadena aleatoria de bits conocida por dos personas y por nadie más. Esta cadena se puede usar como base de un cifrado impenetrable para transmitirse mensajes secretos entre ambas.
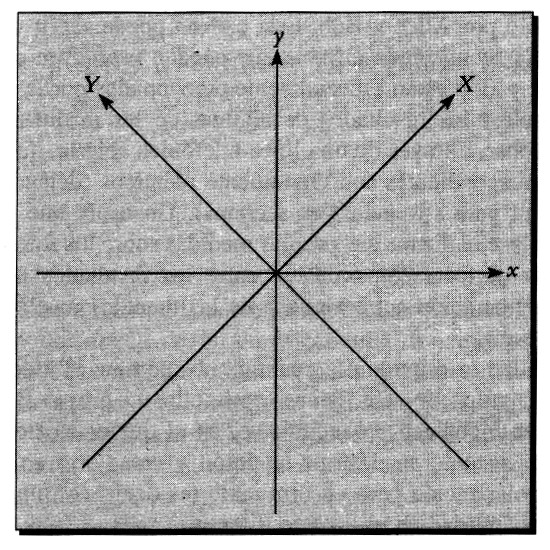
El método funciona más o menos de la siguiente forma. Supongamos que Alice y Bob disponen de un suministro estable de pares de fotones EPRB. De cada par, un fotón llega a Alice y otro a Bob. Previamente acuerdan hacer una larga serie de medidas de la polarización plana de sus fotones respectivos, distinguiendo la mitad de las veces entre dos direcciones perpendiculares, llamadas x e y, y la otra mitad entre otras dos direcciones perpendiculares (en medio de x e y), llamadas X e Y. (Los ejes X e Y se obtienen girando 45° los ejes x e y, como muestra la ilustración de la Figura 11). Para cada uno de sus fotones, Alice elige al azar si medirá su polarización respecto a los ejes x e y o respecto a los ejes X e Y. Bob por su parte hace lo mismo.

Figura 11. Ejes de polarización usados en criptografía cuántica
Una vez han terminado, Alice comunica a Bob la clase de medidas que ha hecho en cada uno de sus fotones, x e y o X e Y, y Bob da a Alice la misma información (la conversación puede hacerse en un teléfono público intervenido por espías sin ningún problema). De esta manera averiguan cuándo hicieron ambos el mismo tipo de medida (lo que habrá sucedido más o menos la mitad de las veces). Para cada medida común, los resultados obtenidos por Alice y Bob deben ser idénticos, a causa del efecto EPRB. Los resultados de esas medidas comunes son conocidos por ambos y por ninguna otra persona (asumiendo que cada uno hizo las medidas en secreto y que no divulgó nada). Estos resultados se pueden representar por una cadena de unos (correspondiente a x o X) y de ceros (correspondiente a y o Y), conocida sólo por Alice y Bob. Esta cadena puede servir como base de un código secreto indescifrable que pueden usar entre ellos.
Si Alice y Bob están especialmente preocupados por la seguridad, pueden emplear los resultados de algunas de las medidas comunes para comprobar, a través de una línea telefónica abierta, que los unos y ceros correspondientes son ciertamente idénticos (dejando el resto de la cadena para sus mensajes secretos). Un espía que de alguna manera hubiese realizado sus propias medidas sobre los fotones habría destruido la perfecta concordancia entre los resultados de Alice y Bob. La comparación entre algunas de las medidas revelaría la presencia del espía.
En realidad la criptografía cuántica no requiere el efecto EPRB. Por ello, un grupo de seis físicos (entre ellos el propio Bennett) ha inventado un ingenioso procedimiento, en el que el efecto EPRB es esencial, consistente en destruir un fotón y crear otro en el mismo estado de polarización pero en otra parte (es decir, con una distribución de probabilidad en el espacio diferente).
A medida que hemos ido sabiendo más cosas sobre las partículas elementales, se ha puesto de manifiesto la notable interrelación entre la aparente complejidad revelada por los experimentos y la simplificación lograda por la teoría. El descubrimiento de gran número de partículas diferentes y de las diversas interacciones entre ellas ha reforzado la impresión de que la física de partículas es complicada. Al mismo tiempo, desde la perspectiva teórica, los progresos en la unificación de la descripción de las partículas y sus interacciones han mostrado su simplicidad subyacente. Aunque la física de las partículas elementales tiene menos de un siglo de edad, quizá hayamos alcanzado ya una fase en que su unidad haya comenzado a revelarse en la forma de un principio único, del cual se espera que pueda predecir la existencia de la diversidad de partículas elementales observadas.