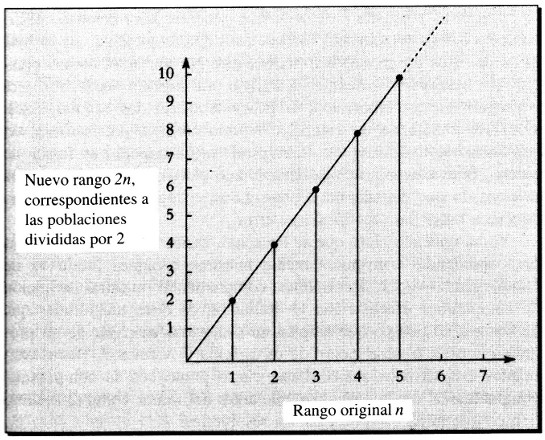
Figura 7. Comportamiento de una ley potencial (en este caso la ley de Zipf original) ante un cambio de escala
El poder de la teoría
La actitud intelectual del científico teórico no sólo es válida para investigar los secretos últimos del universo, sino también para otras muchas tareas. Todo lo que nos rodea son, a fin de cuentas, hechos relacionados entre sí. Naturalmente, pueden considerarse como entidades separadas y estudiarse de esta forma; no obstante, ¡qué diferentes resultan cuando los contemplamos como parte de un todo! Muchos elementos dejan de ser sólo detalles para memorizar: sus relaciones permiten elaborar una descripción comprimida, una forma de teoría, un esquema que los comprenda y resuma y en cuyo marco comienzen a tener sentido. El mundo se hace más comprensible.
El reconocimiento de formas es algo natural para los seres humanos; después de todo, nosotros mismos somos sistemas complejos adaptativos. Poseemos en nuestra naturaleza, tanto por herencia biológica como por transmisión cultural, la capacidad de reconocer patrones, identificar regularidades, construir esquemas mentales. A menudo, estos esquemas son favorecidos o relegados, aceptados o rechazados, en respuesta a presiones selectivas muy diferentes de las que operan en el mundo de la ciencia, donde es tan fundamental el acuerdo con la experiencia.
Las aproximaciones acientíficas para la elaboración de modelos del mundo que nos rodea han caracterizado el pensamiento humano desde tiempos inmemoriales, y siguen estando muy extendidas. Tomemos, por ejemplo, la magia simpática basada en la consideración de que las cosas similares están relacionadas. Para mucha gente de todo el mundo resulta natural, cuando hace falta que llueva, ejecutar una ceremonia en la que se derrame en el suelo agua proveniente de algún lugar especial. La semejanza entre la acción realizada y el fenómeno deseado sugiere que debería existir una conexión causal entre ambos. Las presiones selectivas que ayudan a mantener tal creencia no incluyen el éxito objetivo, el criterio aplicado en la ciencia (al menos, cuando la ciencia funciona correctamente). En su lugar operan otros tipos de selección. Por ejemplo, puede haber ciertos individuos investidos de poder que ejecuten la ceremonia y estimulen la creencia con objeto de perpetuar su autoridad.
La misma sociedad puede estar familiarizada con la magia simpática que opera a través de un efecto sobre la gente, como, por ejemplo, comer el corazón de un león para aumentar la bravura de un guerrero. En este caso puede obtenerse algún éxito objetivo, simplemente por efectos psicológicos: si un hombre cree que lo que ha ingerido lo hará más valiente, eso puede darle la convicción necesaria para actuar valientemente. Análogamente, la brujería destructiva (basada o no en la magia simpática) puede tener un éxito objetivo si la víctima cree en ella y sabe que se le está practicando. Pongamos por caso que alguien quiere hacerme daño y construye un muñeco de cera a imagen mía en el que pega algunos cabellos y recortes de uña mios, y después le clava agujas. Si yo creo, aunque sea sin convicción, en la eficacia de tal magia y sé que alguien la está empleando contra mí, puedo llegar a sentir dolor en los lugares precisos y enfermar (y en un caso extremo, incluso morir) por efectos psicosomáticos. El éxito ocasional (¡o frecuente!) de la magia simpática en tales casos puede promover la creencia de que tales métodos funcionan, incluso cuando, como en la ceremonia para invocar la lluvia, no puede obtenerse un éxito objetivo, excepto por casualidad.
Volveremos al tema de los modelos acientíficos, y las muchas razones para recurrir a ellos, en el capítulo sobre superstición y escepticismo. Lo que ahora nos interesa es el valor de la teorización científica sobre el mundo que nos rodea, viendo cómo encajan en su justo lugar las conexiones y relaciones observadas.
Mucha gente parece tener dificultades con el concepto de teoría, comenzando por la propia palabra, empleada comúnmente con dos significados bastante diferentes. Por un lado, puede significar un sistema coherente de leyes y principios, una explicación más o menos verificada o establecida que da cuenta de hechos o fenómenos conocidos. Por otro, puede referirse a una suposición, una conjetura, una hipótesis no comprobada, una idea o una opinión. Aquí se emplea la palabra en su primera acepción, pero mucha gente, cuando oye hablar de «teoría» o de «teórico», piensa en la segunda. Cuando estudiamos la propuesta de financiación de un proyecto de investigación algo atrevido uno de mis colegas en la junta directiva de la Fundación John D. y Catherine T. MacArthur suele decir: «Creo que deberíamos darle una oportunidad y financiarlo, pero vayamos con cuidado en no gastar dinero en nada teórico». Para un físico teórico profesional, estas palabras deberían resultar una provocación, pero entiendo que mi colega y yo empleamos la palabra «teórico» en sentido diferente.
Puede resultar útil teorizar sobre casi cualquier aspecto del mundo que nos rodea. Consideremos los topónimos como ejemplo. A los habitantes de California, familiarizados con los nombres hispánicos de los pueblos de la costa, no les sorprende que muchos de ellos estén relacionados con la religión católica, de la cual eran devotos practicantes los conquistadores y colonos españoles. No obstante, poca gente se pregunta por qué cada lugar recibió el nombre que tiene. Parece razonable investigar si hay algún proceso sistemático detrás de nombres de santos tales como San Diego, Santa Catalina y Santa Bárbara, así como otros nombres religiosos como Concepción o Santa Cruz, dados a islas, bahías y cabos a lo largo de la costa. Encontramos una pista cuando descubrimos sobre el mapa Punta Año Nuevo. ¿Podrían los otros nombres referirse también a días del año? ¡Naturalmente! En el calendario católico romano encontramos, además del día de año nuevo en el 1 de enero, los siguientes días:
| San Diego |
(San Diego de Alcalá de Henares) 12 de noviembre |
| Santa Catalina |
(Santa Catalina de Alejandría) 25 de noviembre |
| San Pedro |
(San Pedro de Alejandría) 26 de noviembre |
| Santa Bárbara |
(Santa Bárbara, virgen y mártir) 4 de diciembre |
| San Nicolás |
(San Nicolás de Mira) 6 de diciembre |
| La Purísima Concepción |
(La Inmaculada Concepción) 8 de diciembre |
Tal vez, durante un viaje de descubrimiento, estos accidentes geográficos recibieron su nombre según los días del año en el orden en que fueron avistados, de sureste a noroeste. Seguramente, los eruditos han verificado en algún registro histórico que, en 1602, el explorador Sebastián Vizcaíno dio nombre a la bahía de San Diego el 12 de noviembre, a la isla de Santa Catalina el 25 de noviembre, a la bahía de San Pedro el 26 de noviembre, a la bahía de Santa Bárbara el 4 de diciembre, a la isla de San Nicolás el 6 de diciembre y a Punta Concepción el 8 de diciembre. Punta Año Nuevo fue, aparentemente, el primer punto avistado el siguiente año, 1603, aunque fue el 3 de enero en vez del día de año nuevo. El 6 de enero, el día de reyes, Vizcaíno dio nombre a Punta Reyes.
La teoría funciona, pero ¿es general? ¿Qué pasa con Santa Cruz? El día de la Santa Cruz es el 14 de septiembre, lo que no encaja en la secuencia. ¿Recibió el nombre en otra expedición descubridora? El esquema comienza a adquirir algo de complejidad. De hecho, muchos de los nombres religiosos españoles a lo largo de la costa fueron asignados en unas pocas expediciones, de modo que la complejidad efectiva no es tan grande.
En este tipo de teorización (la construcción de un esquema aproximado para describir los resultados de la actividad humana) pueden encontrarse excepciones arbitrarias, que, afortunadamente, no infestan esquemas tales como las ecuaciones de Maxwell para el electromagnetismo. La isla de San Quintín, por ejemplo, situada al norte de San Francisco y conocida por su prisión estatal, parece a primera vista haber recibido su nombre de algún conquistador español el día de San Quintín. Sin embargo, una investigación cuidadosa revela que el «San» fue añadido por error al nombre original de Quintín, un jefe indio capturado allí en 1840.
En el ejemplo de los topónimos, la elaboración de una teoría ha conducido no sólo a la identificación de las regularidades presentes, sino también a una explicación plausible y a su posterior confirmación. Es la situación ideal. A menudo, sin embargo, nos encontramos con situaciones menos claras. Podemos hallar regularidades, predecir la aparición de regularidades similares en otras partes, descubrir que las predicciones se confirman e identificar así un modelo sólido; no obstante, puede tratarse de un modelo cuya explicación continúe escapándose. En este caso, hablamos de una teoría «empírica» o «fenomenológica», pomposas palabras que significan básicamente que vemos que algo sucede, pero no podemos explicarlo. Hay multitud de leyes empíricas que relacionan entre sí hechos de la vida cotidiana.
Tomemos un libro sobre datos estadísticos, como el World Almanac. Hojeándolo, encontraremos una lista de las áreas metropolitanas estadounidenses junto con su número de habitantes en orden decreciente. También encontraremos listas de ciudades de estados individuales, así como de países extranjeros. En cada lista, puede asignarse a cada ciudad un rango, igual a 1 para la ciudad más poblada, 2 para la segunda más poblada, y así sucesivamente. ¿Existe una regla general para todas estas listas que describa cómo disminuye la población a medida que el rango asignado aumenta? Efectivamente, con una buena aproximación, la población es inversamente proporcional al rango asignado; en otras palabras, las sucesivas poblaciones son aproximadamente proporcionales a 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10, 1/11, y así sucesivamente.
Echemos ahora un vistazo a la lista de las mayores empresas, en orden decreciente de volumen de negocio (por ejemplo, el importe de las ventas realizadas en un año dado). ¿Hay alguna regla aproximada que nos diga cómo varían con el rango las cifras de ventas de las empresas? Sí, y es la misma ley que para las poblaciones. El volumen de negocio es, de manera aproximada, inversamente proporcional al rango de la empresa.
¿Qué sucede con el valor monetario de las exportaciones anuales de un país determinado en orden decreciente? Aparece de nuevo la misma ley como una buena aproximación.
Una interesante consecuencia de esta ley se puede verificar fácilmente examinando una de las listas mencionadas, por ejemplo la de ciudades y sus poblaciones. En primer lugar, prestemos atención al tercer dígito de la cifra de cada población. Como es de esperar, está distribuido aleatoriamente; los números 0, 1, 2, etc. en la tercera posición se hallan distribuidos aproximadamente por igual. Una situación completamente distinta se obtiene para la distribución de los primeros dígitos. Existe una enorme preponderancia del 1, seguido del 2, y así sucesivamente. El porcentaje de cifras de población que comienzan con un 9 es extremadamente pequeño. Este comportamiento del primer dígito viene predicho por la ley anterior, que si fuese obedecida exactamente daría una proporción de 45 a 1 del 1 respecto del 9.
| Rango | Ciudad | Población (1990) | Ley de Zipf original 10.000.000 dividido por n | Ley de Zipf modificada 5.000.000 dividido por (n-2/5)3/4 |
|---|---|---|---|---|
|
|
||||
| 1 | Nueva York | 7.322.564 | 10.000.000 | 7.334.265 |
| 7 | Detroit | 1.027.974 | 1.428.571 | 1.214.261 |
| 13 | Baltimore | 736.014 | 769.321 | 747.639 |
| 19 | Washington, D.C. | 606.900 | 526.316 | 558.258 |
| 25 | Nueva Orleans | 496.938 | 400.000 | 452.656 |
| 31 | Kansas City, Mo. | 434.829 | 322.581 | 384.308 |
| 37 | Virginia Beach, Va. | 393.089 | 270.270 | 336.015 |
| 49 | Toledo | 332.943 | 204.082 | 271.639 |
| 61 | Arlington, Texas | 261.721 | 163.934 | 230.205 |
| 73 | Baton Rouge, La. | 219.531 | 136.986 | 201.033 |
| 85 | Hialeah, Fla. | 188.008 | 117.647 | 179.243 |
| 97 | Bakerfield, Calif. | 174.820 | 103.093 | 162.270 |
|
|
||||
Figura 6. Poblaciones de ciudades estadounidenses (según datos del 1994 World Almanac) comparadas con la ley de Zipf original y con una versión modificada de ésta.
¿Qué ocurre si dejamos de lado el World Almanac y tomamos un libro de códigos secretos que contenga una lista de las palabras más comunes en cierto tipo de textos en castellano, ordenadas en orden decreciente según la frecuencia con que aparecen? ¿Cuál es la ley aproximada para la frecuencia de cada palabra en función de su posición en la lista? De nuevo encontramos la misma ley, válida también para otros idiomas.
Todas estas relaciones fueron descubiertas en los años treinta por George Kingsley Zipf, un profesor de alemán de Harvard, y todas ellas representan variaciones de lo que actualmente llamamos ley de Zipf. En la actualidad consideramos que la ley de Zipf es uno de los muchos ejemplos de las llamadas leyes de escala o leyes potenciales, comunes en muchas áreas de la física, la biología y las ciencias del comportamiento. Pero en los años treinta estas leyes constituían una novedad.
En la ley de Zipf, la magnitud considerada es inversamente proporcional al rango, es decir, proporcional a 1, 1/2, 1/3, 1/4, etc. Benoît Mandelbrot ha demostrado que se puede obtener una ley potencial más general (casi la más general) sometiendo esta secuencia a dos modificaciones. La primera consiste en añadir una constante al rango, lo que da 1/(1+constante), 1/(2+constante), 1/(3+constante), 1/(4+constante), etc. La siguiente da cabida, en lugar de estas fracciones, a sus cuadrados, cubos, raíces cuadradas o cualesquiera otras potencias. La elección de los cuadrados, por ejemplo, daría lugar a la siguiente sucesión: 1/(1+constante)2, 1/(2+constante)2, 1/(3+constante)2, 1/(4+constante)2, etc. La ley de Zipf corresponde a una ley potencial de exponente 1, 2 en el caso de los cuadrados, 3 para los cubos, 1/2 para las raíces cuadradas, etc. Las matemáticas permiten también potencias fraccionarias, como 3/4 o 1,0237. En general, podemos considerar la potencia como 1 más una segunda constante. Tal como se añadía una primera constante al rango, así se suma una segunda a la potencia. La ley de Zipf es entonces el caso particular en que ambas constantes valen cero.
La generalización de Mandelbrot de la ley de Zipf es todavía muy simple: la complejidad adicional reside únicamente en la introducción de las dos constantes ajustables, una sumada al rango y otra a la potencia 1. (Por cierto, una constante ajustable se denomina «parámetro», palabra mal empleada últimamente, tal vez por la influencia de otra palabra similar, «perímetro». La ley potencial modificada tiene dos parámetros.) En cada caso, en lugar de comparar los datos con la ley de Zipf original, uno puede introducir estas dos constantes y determinarlas para que se ajusten óptimamente a los datos. En la tabla de la Figura 6 puede verse cómo una versión ligeramente modificada de la ley de Zipf se ajusta significativamente mejor a unas cifras de población que la ley original (con ambas constantes iguales a cero), la cual funciona ya bien de por sí. «Ligeramente modificada» significa que las nuevas constantes de la ley modificada tienen valores bastante pequeños. (Las constantes para la tabla mencionada se ajustaron por mera inspección de los datos. Un ajuste óptimo habría producido un mejor acuerdo con las poblaciones reales.)
Cuando Zipf describió su ley por primera vez, en una época en que se conocían muy pocas leyes de escala, declaró que su principio distinguía las ciencias de la conducta de las físicas, en las que se suponía que no existían este tipo de leyes. En la actualidad se han descubierto tantas de estas leyes en física que estos comentarios tienden a menoscabar la reputación de Zipf más que a aumentarla. Se dice que había otra causa de su mala fama, a saber, una cierta simpatía por las reordenaciones territoriales europeas por parte de Hitler, simpatía que tal vez justificaba porque las conquistas tendían a modificar las poblaciones europeas de modo que concordaban más exactamente con su ley.
Sea o no cierta, esta historia nos enseña una importante lección acerca de las aplicaciones políticas de las ciencias del comportamiento: el que ciertas relaciones tiendan a darse no significa necesariamente que sean siempre deseables. Me encontré con este mismo problema en un reciente seminario en el Instituto de Aspen, en el que mencioné que ciertas distribuciones de riquezas o ingresos tendían, bajo ciertas condiciones, a seguir leyes de escala. Inmediatamente me preguntaron si tal situación podía considerarse como algo bueno. Según recuerdo, me encogí de hombros. Después de todo, la pendiente de la distribución, que determina el grado de desigualdad en las riquezas o los ingresos, depende de la potencia que se dé en la ley.
La ley de Zipf carece de explicación, y lo mismo puede decirse de la gran mayoría de las otras leyes potenciales. Benoît Mandelbrot, que ha hecho contribuciones realmente importantes al estudio de estas leyes (especialmente en conexión con los fractales), admite con gran franqueza que su carrera científica se ha visto coronada por el éxito debido en gran medida a que siempre ha puesto mayor empeño en hallar y describir nuevas leyes potenciales que en intentar explicarlas. (En su libro La geometría fractal de la naturaleza se refiere a su «inclinación a dar preponderancia a las consecuencias por encima de las causas»). Sin embargo, señala con prontitud que en algunos campos, especialmente las ciencias físicas, se han desarrollado explicaciones bastante convincentes. Por ejemplo, el fenómeno del caos en dinámica no lineal está íntimamente relacionado con los fractales y las leyes potenciales, en una forma bastante bien comprendida. Benoît ha construido también de vez en cuando modelos que exhiben leyes potenciales. Por ejemplo, ha calculado la distribución de frecuencias de longitudes de palabra en los textos tecleados por nuestros monos escritores; se ajusta a una versión modificada de la ley de Zipf, con una potencia que se aproxima a 1 (la ley original) al aumentar el número de símbolos. (También ha descubierto que cuando se ajusta a una ley de Zipf la distribución de frecuencias de longitudes de palabra en los textos reales, escritos en lenguajes naturales, la potencia puede diferir significativamente de 1, con una desviación que depende de la riqueza de vocabulario del texto en cuestión.
En los últimos años se ha progresado en la explicación de ciertas leyes potenciales. Uno de los caminos seguidos es la llamada «criticalidad autoorganizada», concepto propuesto por el físico teórico danés Per Bak, en colaboración con Chao Tang y Kurt Wiesenfeld. La aplicación inicial consistió en el estudio de montones de arena, como los que podemos ver en el desierto o en la playa. Los montones son aproximadamente cónicos, y cada uno tiene una pendiente más o menos bien definida. Si examinamos estas pendientes, descubrimos que casi todas tienen el mismo valor. ¿Cómo se explica? Supongamos que el viento deposita constantemente granos de arena adicionales sobre los montones (o un físico en el laboratorio deja caer grano a grano arena de un depósito sobre un montón experimental). Al crecer el montón, la pendiente lateral aumenta, pero solamente hasta un valor crítico. Una vez que se alcanza esta pendiente crítica, la adición de más arena produce avalanchas que disminuyen la altura del montón.
Si la pendiente es mayor que la crítica, se produce una situación inestable en la que las avalanchas se dan con frecuencia, reduciendo la pendiente hasta que su valor desciende por debajo del crítico. Los montones de arena se ven «atraídos» de modo natural hacia el valor crítico de la pendiente, sin que sea precisa ninguna influencia externa (de aquí el nombre «criticalidad autoorganizada»).
El tamaño de una avalancha se define por el número de granos de arena que participan en ella. La experiencia revela que, cuando el valor de la pendiente está próximo al crítico, los tamaños de las avalanchas siguen con buena aproximación una ley potencial.
En este caso, la constante que hay que añadir a la ley de Zipf es muy grande. En otras palabras, si se asigna un rango numérico a las avalanchas según su tamaño, entonces el número de granos que participan en ellas decrece muy rápidamente con dicho rango. La distribución de las avalanchas en los montones de arena es un ejemplo de ley potencial que ha sido estudiado satisfactoriamente tanto por métodos teóricos como experimentales. Bak y sus colegas reprodujeron, por medio de una simulación numérica, tanto la ley potencial como el valor aproximado de su exponente.
A pesar del fuerte descenso en el tamaño al aumentar el rango asignado, están presentes prácticamente todas las escalas de tamaño de avalancha posibles. En general, una distribución que satisfaga una ley potencial es «independiente de la escala»; por ello, las leyes potenciales se llaman también «leyes de escala». Pero ¿qué significa exactamente que una ley de distribución sea independiente de la escala?
La independencia de la escala de las leyes potenciales queda bien ilustrada por la ley de Zipf original, la cual establece, por ejemplo, que las poblaciones de las ciudades son proporcionales a 1/1 : 1/2 : 1/3 : 1/4 : 1/5 … Para simplificar, supongamos que corresponden a un millón, medio millón, un tercio de millón, etc. Multipliquemos estas poblaciones por una fracción dada, por ejemplo, 1/2; las nuevas poblaciones, en millones de habitantes, son ahora 1/2, 1/4, 1/6, 1/8, 1/10 … Son justamente las poblaciones asignadas a los antiguos rangos 2, 4, 6, 8, 10, … De modo que dividir por dos los valores de las poblaciones equivale a doblar los rangos de las ciudades, pasando de la secuencia 1, 2, 3, 4, … a la secuencia 2, 4, 6, 8, 10, … Si representamos gráficamente los nuevos rangos en función de los antiguos, el resultado es una línea recta, como el diagrama mostrado en la Figura 7.
Esta relación lineal entre rangos puede servir como definición de ley de escala para cualquier magnitud: la reducción de todos los valores por cualquier factor constante (1/2 en el ejemplo) equivale a asignar nuevos rangos en el conjunto original de valores, y de ese modo los nuevos rangos son una función lineal de los antiguos. (Los nuevos rangos no serán siempre números enteros, pero en cualquier caso la fórmula para los tamaños en función del rango producirá siempre una curva regular que puede emplearse para interpolar entre números enteros.)
En el caso de las avalanchas en montones de arena, como sus tamaños se distribuyen según una ley potencial, una reducción por cualquier factor común es equivalente a una simple reasignación de los rangos en la secuencia original de avalanchas. Resulta evidente que en dicha ley no se ha seleccionado ninguna escala particular, excepto en los dos extremos del espectro de tamaños, donde aparecen limitaciones obvias. Ninguna avalancha puede incluir menos de un grano de arena y, evidentemente, la ley potencial debe dejar de aplicarse en la escala de un único grano; en el otro extremo del espectro, ninguna avalancha puede ser mayor que la totalidad del montón en cuestión, de modo que a la mayor avalancha posible se le asigna, por definición, rango uno.
Las consideraciones sobre la mayor avalancha posible nos recuerdan una característica común de las distribuciones potenciales de magnitud en sucesos naturales. Los eventos mayores o más catastróficos, con rangos numéricos muy pequeños, pueden considerarse, pese a situarse más o menos en la curva dictada por la ley potencial, como sucesos históricos individuales de los que se derivan consecuencias muy importantes. Por su parte, los sucesos menores, con un rango numérico muy grande, se consideran sólo desde un punto de vista meramente estadístico. Los grandes terremotos, con un índice del orden de 8,5 en la escala de Richter, se recuerdan en los titulares de la prensa y en los libros de historia (especialmente si devastan alguna gran ciudad). Los registros de la multitud de terremotos de índice 1,5 languidecen en las bases de datos de los sismólogos, y su destino es, fundamentalmente, el análisis estadístico. Charles Richter y su maestro Beno Gutenberg, ambos colegas ya fallecidos de Caltech, descubrieron hace ya mucho tiempo que la energía liberada en un terremoto sigue una ley potencial. (Un día de 1933, Gutenberg estaba manteniendo una conversación tan intensa con Einstein sobre sismología que ninguno de los dos percibió el terremoto de Long Beach que sacudió el campus de Caltech.) De igual manera, los pequeños meteoritos que constantemente se estrellan contra la Tierra únicamente se registran en los estudios estadísticos de los especialistas, mientras que el colosal impacto que contribuyó a la extinción masiva del Cretáceo, hace 65 millones de años, está considerado como el suceso individual de mayor importancia en la historia de la biosfera.
Puesto que se ha demostrado que las leyes potenciales operan en los fenómenos de criticalidad autoorganizada, la ya popular expresión «autoorganizado» se está convirtiendo en moneda común, a menudo asociada con el término «emergente». Muchos científicos, entre los que se cuentan miembros de la familia del Instituto de Santa Fe, intentan comprender el fenómeno de la aparición de estructuras sin que medien condiciones especiales impuestas desde el exterior. Estructuras o comportamientos aparentemente complejos pueden surgir en una asombrosa variedad de contextos en el seno de sistemas caracterizados por reglas muy simples. De estos sistemas se dice que son autoorganizados, y sus propiedades, emergentes. El mayor ejemplo es el propio universo, cuya complejidad emerge de un conjunto de leyes simples a las que se suma el azar.

Figura 7. Comportamiento de una ley potencial (en este caso la ley de Zipf original) ante un cambio de escala
En muchos casos, el estudio de estas estructuras se ha visto facilitado en gran medida por el desarrollo de los modernos ordenadores. A menudo resulta más fácil seguir la emergencia de nuevos rasgos por medio de un ordenador que a través de ecuaciones en una hoja de papel. Los resultados son especialmente sorprendentes en aquellos casos en los que la emergencia requiere un gran lapso de tiempo real, pues la computadora puede acelerar el proceso por un factor gigantesco. No obstante, el cálculo por ordenador puede requerir un elevado número de pasos, lo que plantea un problema totalmente nuevo.
En nuestra descripción de la complejidad hemos considerado hasta ahora descripciones comprimidas de un sistema o de sus regularidades (o programas cortos de ordenador que generen descripciones codificadas) y hemos relacionado varias clases de complejidad con la longitud de estos programas o descripciones. No obstante, hemos prestado poca atención al tiempo, al trabajo o al ingenio necesarios para conseguir dicha compresión, o para identificar las regularidades. Como el trabajo de un científico teórico consiste precisamente en reconocer regularidades y en comprimir su descripción en forma de teorías, prácticamente hemos despreciado el valor del trabajo de los teóricos, lo que ciertamente representa un crimen monstruoso. Algo debemos hacer para rectificar ese error.
Ya ha quedado claro que se necesitan varios conceptos diferentes para aprehender convenientemente nuestras nociones intuitivas de complejidad. Ahora necesitamos complementar nuestra definición de complejidad efectiva con la definición de otras magnitudes que describirán el tiempo que emplea un ordenador en pasar de un programa corto a la descripción de un sistema, y viceversa. (Estas cantidades estarán relacionadas hasta cierto punto con la complejidad computacional de un problema, que antes definimos como el mínimo tiempo que tarda un ordenador en resolverlo.)
Estos conceptos relativos a la complejidad han sido objeto de estudio por parte de varios científicos, pero Charles Bennet, un brillante pensador de IBM, los ha tratado de un modo especialmente elegante. Charlie trabaja en IBM, y la empresa le proporciona tiempo para tener ideas, publicarlas y dar seminarios aquí y allá para hablar de ellas. Me gusta comparar sus peregrinaciones con las de los trovadores del siglo XII, que viajaban de corte en corte por lo que ahora es el sur de Francia. En lugar de canciones sobre el amor cortesano, Charlie «canta» sobre complejidad y entropía, ordenadores cuánticos y cifrado cuántico. He tenido el placer de trabajar con él en Santa Fe y en Pasadena, durante una estancia con nuestro grupo en Caltech.
Existen dos magnitudes particularmente interesantes relacionadas con la complejidad computacional, denominadas por Charlie «profundidad» y «cripticidad», con una relación recíproca. El estudio de ambas resulta muy útil en el caso de un sistema aparentemente complejo y que posee no obstante un contenido de información algorítmica y una complejidad efectiva bajos, pues se puede generar su descripción por medio de un programa muy corto. El truco consiste en preguntarse: 1) ¿Cuánto cuesta pasar del programa corto o esquema altamente comprimido a una descripción completamente desarrollada del propio sistema o de sus regularidades? 2) ¿Cuánto cuesta, partiendo del sistema, comprimir su descripción (o una descripción de sus regularidades) en un programa o esquema?
De manera aproximada, la profundidad es una medida del primer tipo de dificultad y la cripticidad del segundo. Evidentemente, el valor asignable al trabajo de un teórico está relacionado con la cripticidad (aunque una descripción más sutil del esfuerzo de elaborar teorías debería incluir una distinción entre el ingenio y la mera laboriosidad).
Para ilustrar cómo una gran simplicidad puede estar asociada con un valor muy grande de la profundidad, retomemos a la conjetura de Goldbach, que afirma que todos los números pares mayores que 2 pueden expresarse como la suma de dos números primos. Como ya se dijo, esta conjetura no ha sido demostrada ni refutada, pero se ha verificado para todos los pares menores que una cierta cota muy grande, merced a la potencia de los ordenadores empleados y a la paciencia de los investigadores.
Previamente nos hemos permitido suponer que la conjetura de Goldbach es técnicamente indecidible (sobre la base de los axiomas de la teoría de números) pero que, de hecho, es cierta en la práctica. Ahora imaginaremos que la conjetura es falsa. En ese caso, existe un número entero par g mayor de 2 y que no puede expresarse como la suma de dos primos. Este número hipotético g tiene una descripción muy simple, justo la que acabamos de dar. Análogamente, existe un programa muy pequeño para calcularlo; por ejemplo, uno puede buscar metódicamente números primos cada vez más grandes y probar la conjetura de Goldbach sobre todos los números desde el 3 hasta el mayor primo hallado. De este modo, podrá descubrirse finalmente el menor número g que viole la conjetura.
Aunque la conjetura de Goldbach sea realmente falsa, es probable que el tiempo de cálculo consumido por tal programa para hallar g sea muy grande de todos modos. En este caso hipotético, el número g tiene un contenido de información algorítmica y una complejidad efectiva pequeños, pero una profundidad considerable.
La definición técnica de profundidad propuesta por Charlie implica un ordenador, del mismo tipo que el considerado en relación con el contenido de información algorítmica: un ordenador ideal polifacético al que se le pueda incrementar, en cualquier momento y según las necesidades, la capacidad de memoria (o que tenga de entrada una memoria infinita). Se parte de un mensaje compuesto por una cadena de bits, que describe el sistema objeto de estudio, y se considera no sólo el programa más corto que hará que el ordenador imprima la cadena y se detenga después (como era el caso en la definición de contenido de información algorítmica), sino todo el conjunto de programas cortos que tengan este efecto. Para cada uno de estos programas, se mira cuál es el tiempo de cálculo empleado por el ordenador para pasar del programa a la cadena original y se promedia este valor sobre el conjunto de todos los programas, empleando un método de promedio que da mayor peso a los programas más cortos.
Bennett ha reformulado ligeramente esta definición sirviéndose de la metáfora de Greg Chaitin. Imaginemos que nuestros monos escritores se ponen a trabajar para componer programas de ordenador en lugar de obras en prosa. Prestemos atención a aquellos programas excepcionales que hacen que el ordenador escriba un cierto mensaje y se detenga luego. De entre todos estos programas, ¿cuál es la probabilidad de que el tiempo de ejecución requerido para uno cualquiera de ellos sea menor que un cierto tiempo T? Llamemos p a esta probabilidad. La profundidad d se define entonces como cierto tipo de promedio de los valores posibles de T, promedio que depende de cómo varía p con T.
La Figura 8 representa aproximadamente la variación de la probabilidad p en función del máximo tiempo de ejecución permitido T. Cuando T es muy pequeño, es muy poco probable que los monos compongan un programa que produzca el resultado deseado en tan poco tiempo, de modo que p es cercano a cero. Cuando T es muy grande, la probabilidad se aproxima obviamente a 1. La profundidad d puede definirse, grosso modo, como lo que tarda en subir la curva de T en función de p. La profundidad indica cuál es el máximo tiempo de ejecución permitido que hay que tomar para seleccionar la mayor parte de los programas que harán que el ordenador imprima nuestro mensaje y después se detenga. La profundidad es en cierto modo una medida del tiempo que tardará en generarse el mensaje.
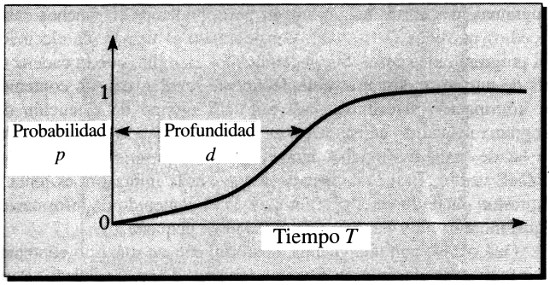
Figura 8. La profundidad como función creciente del tiempo
En la naturaleza, el hecho de que un sistema posea una profundidad muy grande nos indica que ha tardado mucho tiempo en evolucionar o bien que tiene su origen en otro sistema al cual le ha llevado mucho tiempo evolucionar a su vez. La gente que muestra interés en la conservación de la naturaleza o en la preservación de monumentos históricos está intentando de hecho preservar la profundidad y la complejidad efectiva, tal como se manifiestan en las comunidades naturales o en la cultura humana.
Pero, como ha demostrado Charlie, la profundidad tiende a manifestarse como el subproducto de un proceso evolutivo prolongado Podemos encontrar muestras de profundidad no sólo en las formas de vida actuales, incluido el hombre, en las magníficas obras de arte producidas por la humanidad o en los restos fósiles de dinosaurios mamíferos de la Era Glacial, sino también en una lata de cerveza vacía abandonada en una playa, o en una pintada sobre la pared de un cañón. Los conservacionistas no están obligados a defender toda las manifestaciones de profundidad.
Aunque la profundidad es un promedio de tiempos de ejecución sobre longitudes de programa, promedio realizado de modo que los programas más cortos tengan mayor peso, podemos en muchos casos hacernos una idea de su valor considerando el tiempo de ejecución del programa más corto. Supongamos, por ejemplo, que la cadena de bits de nuestro mensaje es completamente regular, con un contenido de información algorítmica casi nulo. El tiempo de ejecución del programa más corto en este caso es bastante reducido —el ordenador no ha de «pensar» mucho para ejecutar un programa como «IMPRIME veinte billones de ceros» (aunque si la impresora es lenta la impresión puede llevar algún tiempo). Si el contenido de información algorítmica es muy bajo, la profundidad es pequeña.
¿Qué ocurre con una cadena aleatoria, con un máximo contenido de información algorítmica para una longitud de mensaje dada? Pasar del programa más corto —IMPRIME seguido de la propia cadena— a la impresión efectiva del mensaje no requerirá tampoco demasiado esfuerzo por parte del ordenador, de modo que cuando el contenido de información algorítmica es máximo la profundidad es igualmente baja. La situación recuerda la variación de la complejidad efectiva máxima con el contenido de información algorítmica, como se representa en la Figura 4. En este caso podemos entender cómo varía la profundidad máxima con el contenido de información algorítmica. Su valor es bajo en ambos extremos, pero puede tener un valor finito entre estos puntos, en la región intermedia entre el orden y el desorden. Naturalmente, en esta región intermedia la profundidad no tiene por qué ser grande.
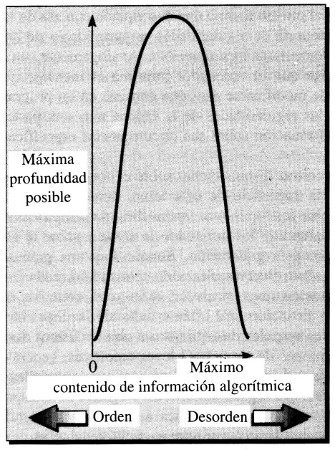
Figura 9. Máxima profundidad posible representada como función aproximada del contenido de información algorítmica
La figura precedente tiene una forma distinta de la correspondiente a la Figura 4; aunque ambas son representaciones aproximadas, muestran que la profundidad puede ser grande incluso para valores del contenido de información algorítmica muy cercanos al orden o al desorden completos, donde la complejidad efectiva es también pequeña.
La definición de cripticidad hace referencia a una operación que es la inversa de la que se considera en la definición de profundidad. La cripticidad de la cadena de bits de un mensaje es el menor tiempo requerido por un ordenador estándar para encontrar, partiendo de la cadena, uno de los programas más cortos que hagan que la máquina imprima el mensaje y después se detenga.
Supongamos que la cadena de bits es el resultado de la codificación del flujo de datos estudiado por un teórico. La cripticidad de la cadena sería entonces una medida aproximada de la dificultad de la tarea del teórico, no muy diferente de la del ordenador en la definición. El teórico identifica tantas regularidades como puede, en forma de información mutua que relaciona diferentes partes del flujo de datos, y luego elabora hipótesis, tan simples y coherentes como le sea posible, que expliquen las regularidades observadas.
Las regularidades son los rasgos comprimibles del flujo de datos. Proceden en parte de las leyes fundamentales de la naturaleza y en parte de sucesos azarosos que pudieron ocurrir de otra forma. Pero el flujo posee también rasgos aleatorios, procedentes de sucesos azarosos que no dieron lugar a regularidades; estos rasgos son incomprensibles. Al comprimir las regularidades tanto como sea posible, el teórico está descubriendo al mismo tiempo una descripción concisa de la totalidad del flujo, compuesta de regularidades comprimidas y de información aleatoria suplementaria incompresible. Análogamente, un programa breve que haga que el ordenador imprima el mensaje (y luego se detenga) puede modificarse para que consista en un programa básico que describa las regularidades de la cadena más una parte adicional que aporte información sobre sus circunstancias específicas accidentales.
Aunque nuestras disquisiciones sobre el concepto de teoría apenas han arañado la superficie de este tema, hemos mencionado ya la teorización sobre los topónimos, sobre fórmulas empíricas en estadística, sobre la altura de los montones de arena y sobre el electromagnetismo clásico y la gravitación. Aunque hay una gran similaridad formal entre estas diversas clases de teorización, cada una implica descubrimientos en muchos niveles diferentes, entre los que resulta útil hacer una distinción. ¿Se están estudiando las leyes básicas de la física? ¿O leyes aproximadas aplicadas a objetos físicos desordenados como los montones de arena? ¿O leyes empíricas, generales aunque aproximadas, sobre instituciones humanas, como ciudades o compañías financieras? ¿O reglas específicas, cargadas de excepciones, sobre los nombres que la gente aplica a una región geográfica determinada? Existen claras e importantes diferencias en exactitud y generalidad entre toda esta diversidad de principios teóricos. Esas diferencias se discuten frecuentemente en términos de cuáles son más fundamentales que los demás. Pero ¿qué significa esto?