Figura 4. Diagrama que muestra a grandes rasgos cómo varía la complejidad efectiva máxima con el contenido de información algorítmica
Un niño aprendiendo a hablar
Cuando mi hija estaba aprendiendo a hablar, una de sus primeras frases era «Daddy go car-car», que recitaba cada mañana cuando me iba a trabajar. Que la frase aludiera a mí me producía una gran satisfacción, y me encantaba que ella estuviese realmente hablando, aunque su inglés todavía necesitara algo de práctica. Hasta hace poco no caí en la cuenta de que ciertos rasgos de la gramática inglesa estaban ya presentes en aquella frase. Pensemos, por ejemplo, en el orden de las palabras. En inglés el sujeto se antepone al verbo (lo que no ocurre en otras lenguas como, por ejemplo, el galés, el hawaiano y el malgache). El sujeto y el verbo estaban correctamente colocados, igual que la expresión «car-car». En la sentencia gramatical inglesa «[Dady] [is going away] [in his car]» el orden de los tres elementos es exactamente el mismo que en la aproximación del bebé.
Naturalmente, a medida que mi hija crecía su gramática mejoraba y en unos pocos años ya hablaba correctamente. Cualquier niño normal al cuidado de una persona que hable un lenguaje particular y lo emplee regularmente para dirigirse a él, aprenderá a hablar de modo gramaticalmente correcto ese mismo lenguaje al cabo de algunos años (aunque más de un norteamericano pensará que esto no es aplicable a muchos estudiantes de enseñanza secundaria). De hecho, la mayoría de niños son capaces de aprender dos y hasta tres lenguas, especialmente cuando el niño es cuidado habitualmente por más de una persona y cada una de ellas le habla regularmente en un lenguaje distinto. El aprendizaje se produce aunque la exposición del niño a un lenguaje particular sea a través de un solo hablante. Pero ¿cómo se las arregla el niño para saber, de entre las maneras posibles de construir un enunciado en un lenguaje dado, cuáles son gramaticales y cuáles no?
Imaginemos que haya sólo cincuenta mil enunciados posibles y que un niño ensaye sistemáticamente cincuenta enunciados nuevos cada día durante mil días, indicándole su madre pacientemente «bien» o «mal» en cada caso. Asumiendo este absurdo planteamiento y una memoria perfecta por parte del niño, éste necesitará un mínimo de tres años para conocer exactamente cuáles de entre los cincuenta mil enunciados posibles son gramaticales.
Un informático diría que este niño ficticio se ha construido un «listado» mental que incluiría todos los enunciados candidatos junto con la etiqueta «gramatical» o «no gramatical». Pero cincuenta mil enunciados es demasiado poco; está claro que los niños reales tienen que aprender de otra manera.
En cualquier lenguaje humano hay un número ilimitado de enunciados posibles, los cuales pueden contener un número arbitrariamente grande de oraciones que a su vez incluyen palabras y expresiones modificadoras. La longitud de un enunciado está limitada sólo por el tiempo disponible y por la paciencia y memoria del hablante y del oyente. Por otro lado, el vocabulario que se maneja suele incluir muchos miles de palabras. No hay modo de que un niño escuche o recite todos los enunciados posibles y elabore con ellos un listado. Es más, una vez completado el proceso real de aprendizaje, un niño puede decir si un enunciado nunca oído con anterioridad es gramatical o no.
Los niños tienen que elaborar, sin tener plena conciencia de ello, un conjunto provisional de reglas acerca de lo que es gramatical y lo que no. Después, a medida que continúan escuchando enunciados gramaticalmente correctos y ensayan ocasionalmente enunciados que les son corregidos, van modificando el conjunto de reglas, de nuevo sin tener necesariamente plena conciencia de ello. En inglés, por ejemplo, resulta fácil para un niño aprender la construcción regular o «débil» del pasado de un verbo añadiendo -ed o -d al presente. Más tarde, cuando se encuentra con irregularidades como sing y sang (presente y pasado del verbo «cantar», un verbo «fuerte»), el niño modifica el conjunto de reglas para incluir esta excepción. Pero esto puede llevarle a pronunciar, por ejemplo, bring y brang en vez de bring y brought (presente y pasado del verbo «traer»), un error que, una vez corregido, conducirá a una nueva modificación de las reglas. De este modo, a través del mejoramiento progresivo del conjunto de reglas internas, en la mente del niño va tomando forma una gramática.
Está claro que, mientras aprende a hablar, el niño hace uso de información gramatical que va adquiriendo año tras año a partir de ejemplos de enunciados gramaticales y no gramaticales. Pero, en vez de construir una lista, el niño comprime de alguna manera esta experiencia en un conjunto de reglas, una gramática interna que se ajusta incluso a enunciados nuevos no escuchados con anterioridad.
Ahora bien, la información obtenida del mundo exterior, por ejemplo de unos padres que hablan la lengua en cuestión, ¿es suficiente para construir tal gramática interna? Para Noam Chomsky y su escuela la respuesta es no: el niño tiene que estar equipado ya desde el nacimiento con una gran cantidad de información aplicable a la gramática de cualquier lengua natural humana. La única fuente plausible de dicha información es una tendencia innata, fruto de la evolución biológica, a hablar lenguas con ciertos rasgos gramaticales generales compartidos por todas las lenguas humanas naturales. La gramática de cada lengua particular contiene también rasgos adicionales no programados biológicamente. Muchos de ellos varían de una lengua a otra, pero otros probablemente son tan universales como los innatos. Son estos rasgos adicionales los que el niño tiene que aprender.
Naturalmente, el que un enunciado sea gramatical no significa que tenga que ajustarse a los hechos. Cualquier hispanohablante sabe que es gramaticalmente correcto decir «el cielo es verde con rayas rojas y amarillas», aunque tal cosa es improbable, por lo menos en la Tierra. Pero hay muchos otros criterios aparte de la mera veracidad que condicionan la elección de los enunciados gramaticales que uno pronuncia en cada ocasión.
Al construir una gramática interna, el niño separa efectivamente los rasgos gramaticales de todos los otros factores, en parte estocásticos, que conducen a los enunciados particulares que escucha. Sólo de este modo es posible la compresión en un conjunto de reglas gramaticales manejable.
El niño exhibe así la primera característica de un sistema complejo adaptativo. Ha comprimido ciertas regularidades identificadas en un cuerpo de experiencia dentro de un esquema que incluye reglas que gobiernan dicha experiencia, pero omite las circunstancias especiales en que las reglas deben aplicarse.
La gramática, sin embargo, no abarca todas las regularidades presentes en una lengua. También hay que considerar las reglas de los sonidos (lo que los lingüistas llaman la «fonética» de un lenguaje), las de la semántica (relativas a lo que tiene sentido y lo que no) y otras. El esquema gramatical, por lo tanto, no incluye todas las reglas del habla, y la gramática no es lo único que se echa en falta cuando se prescinde arbitrariamente de algún rasgo de la sucesión de datos lingüísticos. De todos modos, la adquisición infantil de una gramática es un ejemplo excelente de la construcción de un esquema, en este caso un esquema parcial.
El proceso de aprendizaje gramatical también pone de manifiesto las otras propiedades del funcionamiento de los sistemas complejos adaptativos. Un esquema está sujeto a variación. Para poner a prueba las diferentes variantes en el mundo real es necesario incorporar detalles adicionales como los que se dejaron de lado en la creación del esquema. De este modo se vuelve a encontrar en el mundo real una sucesión de datos de la misma clase que aquella de la que el esquema fue abstraído previamente. Finalmente, lo que ocurre en el mundo real determina qué variantes sobreviven.
En la adquisición de la gramática inglesa, el esquema varía cuando, por ejemplo, la regla de construcción del pasado simple de un verbo con la terminación -ed o -d es modificada por excepciones como sing-sang y bring-brought. Para poner a prueba estas variantes, el niño tiene que hacer uso del esquema en un enunciado real, restituyendo las circunstancias especiales eliminadas para hacer el esquema posible. El niño puede decir, por ejemplo, «We sang a hymn yesterday morning» [Cantamos un himno ayer por la mañana]. El enunciado es satisfactorio. Si, en cambio, el niño dice «I brang home something to show you» [Traje algo a casa para enseñártelo], el padre podría replicar: «Es muy amable por tu parte enseñarme esta cucaracha que encontraste en casa de tía Bessie, pero deberías decir I brought…». Como resultado de esta experiencia, es probable que en el futuro el niño ensaye un nuevo esquema que dé cabida a ambas irregularidades (naturalmente, en muchos casos el esquema se pone a prueba simplemente cuando el niño escucha hablar a alguien).
El funcionamiento de un sistema complejo adaptativo se muestra en el diagrama de la Figura 2. Puesto que un sistema complejo adaptativo extrae regularidades de entre lo aleatorio, es posible definir la complejidad en términos de la longitud del esquema empleado por un sistema complejo adaptativo para describir y predecir las propiedades de una sucesión de datos de entrada. Naturalmente, estos datos son por lo general relativos al funcionamiento de algún otro sistema que está siendo observado por el sistema complejo adaptativo considerado.
La utilización de la longitud de un esquema no significa una vuelta al concepto de complejidad bruta, pues el esquema no constituye una descripción completa de la sucesión de datos o del sistema observado, sino tan sólo de las regularidades abstraídas a partir de los datos disponibles. En algunos casos, como en el de la gramática, sólo se incluye un cierto tipo de regularidades, dejando aparte el resto, y el resultado es un esquema parcial.
Se podría concebir la complejidad gramatical en términos de un libro de texto de gramática. En pocas palabras, cuanto más largo es el texto más compleja es la gramática. Esto concuerda muy bien con la noción de complejidad como longitud de un esquema. Cada una de las pequeñas y fastidiosas excepciones incrementa la extensión del libro y la complejidad gramatical del lenguaje.
Aquí vuelven a aparecer fuentes de arbitrariedad tales como la resolución y el conocimiento o entendimiento compartidos inicialmente. En el caso de un libro de gramática, la resolución se corresponde con el grado de detalle alcanzado en el texto. ¿Se trata de una gramática muy elemental que deja de lado muchas excepciones y reglas poco claras, tratando sólo los puntos principales que necesita un viajero al que no le preocupe equivocarse de vez en cuando? ¿O se trata de un voluminoso tomo académico? Si es así, ¿es uno de los viejos textos familiares o una gramática generativa de las que se han puesto ahora de moda? Es obvio que la longitud del libro dependerá de tales distinciones. En cuanto al conocimiento inicial, considérese una gramática clásica de una lengua extranjera escrita en inglés para angloparlantes. Si se trata de una gramática holandesa (estrechamente relacionada con la inglesa y con similitudes evidentes), el número de conceptos gramaticales nuevos que habrá que introducir será bastante inferior al que habría que introducir en el caso del idioma navajo, cuya estructura es muy diferente de la del inglés. La gramática del navajo tendría que ser más larga. Del mismo modo, una hipotética gramática holandesa escrita para hablantes navajos tendría que ser presumiblemente más larga que una gramática holandesa escrita para ingleses.
Aun teniendo en cuenta estos factores, sigue siendo razonable relacionar la complejidad gramatical de una lengua con la longitud de un texto que describa su gramática. Sin embargo, sería más interesante poder mirar dentro del cerebro de un hablante nativo (cosa que los avances tecnológicos quizás hagan posible algún día) y observar cómo está codificada en él la gramática. La longitud del esquema representado por esta gramática interna proporcionaría una medida algo menos arbitraria de la complejidad gramatical. (Naturalmente, la definición de longitud en este caso puede ser sutil, dependiendo del modo en que esté codificada la información gramatical. ¿Está inscrita localmente en neuronas y sinapsis o distribuida de algún modo en una red general?)
Definimos la complejidad efectiva de un sistema, relativa a un sistema complejo adaptativo observador, como la longitud del esquema utilizado para describir sus regularidades. Podemos emplear el término «complejidad efectiva interna» cuando el esquema gobierna de algún modo el sistema objeto de discusión (igual que la gramática inscrita en el cerebro regula el habla) en vez de limitarse a ser un mero recurso de un observador externo, como el autor de un texto gramatical.
La utilidad del concepto de complejidad efectiva, especialmente cuando no es interna, depende de si el sistema complejo adaptativo observador es competente a la hora de identificar y comprimir regularidades y descartar lo que es incidental. Si no es así, la complejidad efectiva del sistema observado tiene que ver más con las limitaciones particulares del observador que con las propiedades del sistema observado. La eficiencia del observador con frecuencia resulta evidente, pero el concepto mismo de eficiencia plantea cuestiones profundas. Ya hemos visto que la noción de compresión óptima puede tropezar con el obstáculo de la no computabilidad. Pero, aparte de la compresión, ¿qué ocurre con la identificación de regularidades? ¿Está realmente bien definido el problema de identificar regularidades a partir de una sucesión de datos?
La tarea sería más fácil si la sucesión de datos fuera, en algún sentido, de longitud indefinida, como en el caso de un discurso o texto tan extenso que comprenda muestras representativas de todos los enunciados posibles (hasta una determinada longitud) que pueden pronunciarse en un lenguaje dado. De este modo hasta la más rara regularidad gramatical se mostraría una y otra vez en condiciones similares, resultando así distinguible de una regla falsa fruto de una mera fluctuación aleatoria (por ejemplo, en un texto corto en inglés el pretérito perfecto podría no aparecer, sugiriendo equivocadamente que en dicha lengua no existe tal tiempo verbal, mientras que en un texto muy largo no es probable que esto ocurra).
Un grupo de físicos teóricos, entre ellos Jim Crutchfield, que trabaja en el Instituto de Santa Fe y en la universidad de California en Berkeley, ha hecho considerables progresos en la distinción entre regularidad y aleatoriedad dentro de una cadena de bits indefinidamente larga. Para ello definen clases que abarcan un abanico de regularidades y muestran cómo podría emplearse en principio un ordenador para encontrar y clasificar cualquier regularidad que caiga dentro de una de estas categorías. Pero estos métodos no proporcionan ningún algoritmo para identificar cada tipo de regularidad. No existe tal algoritmo. Sin embargo demuestran que en cuanto un computador ha encontrado regularidades pertenecientes a ciertas clases en una cadena de bits, puede deducir la presencia de nuevas regularidades pertenecientes a una clase más amplia e identificarlas. Esto es lo que se llama «aprendizaje jerárquico».
Por lo general, una clase de regularidades corresponde a un conjunto de modelos matemáticos para generar una sucesión de datos. Supongamos que la sucesión de datos es una cadena de bits que se sabe generada por un proceso al menos en parte estocástico, como el lanzamiento de una moneda. Un ejemplo muy simple de conjunto de modelos sería entonces el que surge de considerar una secuencia de lanzamientos de una moneda trucada, en que la probabilidad de que salga cara (un 1 en la cadena de bits) es algún valor fijo entre 0 y 1, distinto para cada modelo, mientras que la probabilidad de que salga cruz (un 0 en la cadena de bits) es 1 menos la probabilidad de que salga cara.
Si la probabilidad de que salga cara es 1/2, cualquier regularidad aparente en la secuencia sería únicamente debida al azar. A medida que la cadena de bits se alarga, la probabilidad de dejarse engañar por tales regularidades aleatorias disminuye, a la vez que aumenta la probabilidad de reconocer que la secuencia corresponde a una moneda no trucada. En el extremo opuesto, consideremos una cadena de dos bits. En el caso de una moneda no trucada, hay una posibilidad sobre cuatro de que ambos bits sean 1 (regularidad perfecta). Pero una secuencia así podría obtenerse también con una moneda de dos caras. Así pues, una corta cadena de bits procedente de una secuencia de lanzamientos de una moneda no trucada puede confundirse a menudo con la de una moneda fuertemente desequilibrada. En general, la ventaja de considerar una sucesión de datos indefinidamente larga es que se incrementa enormemente la posibilidad de discriminar entre modelos distintos, correspondiendo cada modelo a una clase particular de regularidades.
Una ligera complicación adicional podría consistir en imponer que todas las secuencias en que salgan dos caras seguidas sean descartadas. La regularidad resultante —que la cadena de bits nunca contendría dos unos seguidos— sería fácil de reconocer en cualquier cadena larga. Una complicación aún mayor podría consistir en descartar todas las secuencias que contengan un número par de caras seguidas.
Cuando un sistema complejo adaptativo recibe una sucesión de datos arbitrariamente larga, por ejemplo en la forma de una cadena de bits, puede dedicarse a buscar sistemáticamente regularidades de una clase dada (correspondientes a modelos de una clase dada), pero no hay ningún procedimiento exhaustivo para buscar todas las regularidades posibles. Cualquier regularidad identificada puede incorporarse entonces en un esquema que describa la sucesión de datos (o un sistema que la genere).
Para identificar regularidades dentro de una sucesión de datos de entrada, un sistema complejo adaptativo típico divide dicha sucesión en numerosas partes comparables entre sí e investiga sus rasgos comunes. La información común a muchas partes, o «información mutua», sirve para diagnosticar regularidades. En el caso de un texto en un lenguaje determinado, los enunciados podrían ser las partes objeto de comparación. La información gramatical mutua entre los distintos enunciados pondría de manifiesto las regularidades gramaticales.
Sin embargo, la información mutua sólo sirve para identificar regularidades, y su magnitud no constituye una medida directa de la complejidad efectiva. Una vez han sido identificadas ciertas regularidades y se ha elaborado una concisa descripción de ellas, es la longitud de la descripción lo que mide la complejidad efectiva.
Supongamos que en el sistema objeto de descripción no hay regularidades de ninguna clase, como ocurriría muchas veces (¡pero no siempre!) con un pasaje tecleado por nuestros proverbiales monos. Un sistema complejo adaptativo sería entonces incapaz de encontrar ningún esquema, pues los esquemas resumen regularidades. En otras palabras, el único esquema posible tendría longitud cero, y el sistema complejo adaptativo asignaría el valor cero a la complejidad efectiva del desorden aleatorio en estudio. Esto es absolutamente apropiado, pues la gramática de un puro galimatías debería tener longitud cero. Aunque el contenido de información algorítmica de una cadena de bits aleatoria de longitud dada es máximo, la complejidad efectiva es cero.
En el otro extremo de la escala, el contenido de información algorítmica de una cadena de bits enteramente regular, por ejemplo una sucesión de unos, es próxima a cero. La complejidad efectiva —la longitud del esquema que describe las regularidades de la cadena de bits— también debería ser próxima a cero, ya que el mensaje «todo 1» es muy corto.
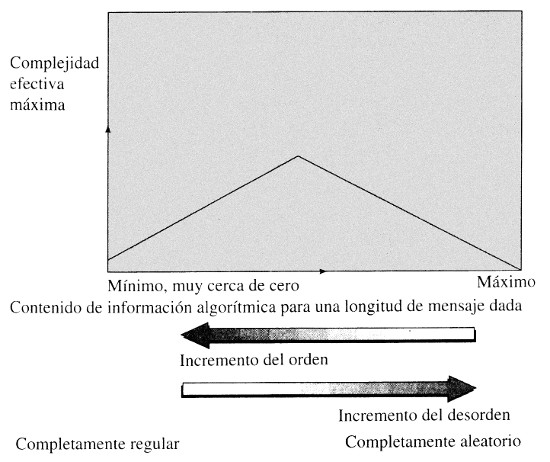
Así pues, para que la complejidad efectiva tenga un valor apreciable el contenido de información algorítmica no debe ser ni demasiado bajo ni demasiado alto; en otras palabras, el sistema no debe estar ni demasiado ordenado ni demasiado desordenado.
El diagrama de la Figura 4 ilustra a grandes rasgos cómo la mayor complejidad efectiva posible de un sistema (relativa a un sistema complejo adaptativo observador) varía con el contenido de información algorítmica, alcanzando valores máximos en la zona intermedia entre el orden excesivo y el desorden excesivo. Muchas magnitudes importantes que surgen en el tratamiento de la simplicidad, la complejidad y los sistemas complejos adaptativos comparten esta misma propiedad.

Figura 4. Diagrama que muestra a grandes rasgos cómo varía la complejidad efectiva máxima con el contenido de información algorítmica
Cuando un sistema complejo adaptativo observa otro sistema e identifica algunas regularidades, el contenido de información algorítmica de la sucesión de datos procedente del sistema observado se expresa como la suma de dos términos: el contenido de información aparentemente regular y el contenido de información aparentemente estocástica. La longitud del esquema —la complejidad efectiva del sistema observado— se corresponde esencialmente con la fracción aparentemente regular del contenido de información. Para una sucesión aleatoria de datos, reconocida como tal, la complejidad efectiva es cero y el contenido de información algorítmica es atribuible en su totalidad al azar. Para una sucesión de datos perfectamente regular (por ejemplo, una larga cadena de bits que sólo contenga unos) el contenido de información algorítmica en su totalidad es regular (no existe fracción estocástica) pero extremadamente pequeño. Las situaciones más interesantes son las que se encuentran entre estos dos extremos, donde el contenido de información algorítmica es apreciable pero no máximo (para la longitud de la sucesión de datos) y es la suma de dos términos significativos, la fracción aparentemente regular (la complejidad efectiva) y la fracción aparentemente estocástica.
Aunque nuestro examen de los sistemas complejos adaptativos arranca con el ejemplo del aprendizaje en el niño, no es necesario acudir a algo tan sofisticado para ilustrar este concepto. También podrían servir nuestros parientes los primates —caricaturizados antes en la historia de la máquina de escribir—, lo mismo que un perro. De hecho, el adiestramiento de nuestras mascotas es una de las maneras de observar procesos de aprendizaje en otros mamíferos.
Enseñar a un perro a estarse quieto supone aplicar una abstracción a gran número de situaciones: permanecer sentado en el suelo, quedarse dentro de un coche con la ventanilla abierta, resistirse a perseguir una tentadora ardilla, etc. El perro aprende, por medio de recompensas y/o castigos, el esquema correspondiente a la orden de estarse quieto. Los esquemas alternativos como, por ejemplo, que haga una excepción a la hora de perseguir gatos, son (al menos en teoría) descartados a medida que progresa el aprendizaje. Pero aunque el perro adopte un esquema como éste estaremos ante el resultado del funcionamiento de un sistema complejo adaptativo. En este caso la competencia entre las presiones del entrenamiento y del instinto cazador habrá propiciado la supervivencia de un esquema distinto al deseado por el adiestrador.
Una vez dada la orden de estarse quieto, el perro entrenado incorpora los detalles apropiados a la situación concreta y aplica el esquema al mundo real en forma de una conducta que es premiada o castigada, lo que contribuye a determinar si el esquema sobrevive o no. Sin embargo, la tendencia a perseguir gatos o ardillas, que también influye en la competencia entre esquemas, no ha sido aprendida por el perro, sino que ha sido programada genéticamente como resultado de la evolución biológica.
Todos los organismos incorporan tales programas. Cuando una hormiga merodea en busca de alimento, sigue una pauta innata que ha evolucionado a lo largo de millones de años. Hace algún tiempo, Herb Simon, un prestigioso experto en psicología, economía e informática de la Universidad de Carnegie-Mellon, se valió de los movimientos de las hormigas para ilustrar el sentido de lo que yo llamo complejidad efectiva. La trayectoria seguida por una hormiga puede parecer compleja, pero las reglas del proceso de búsqueda son simples. La intrincada trayectoria de la hormiga manifiesta una elevada complejidad algorítmica, de la que sólo una pequeña parte es atribuible a las reglas que subyacen a las regularidades de la búsqueda. Pero esta pequeña parte constituye —al menos aproximadamente— la totalidad de la complejidad efectiva. El contenido de información algorítmica restante, el grueso de la complejidad aparente, es resultado de rasgos aleatorios del terreno explorado por la hormiga. (Hace poco hablé de este asunto con Herb, quien al final exclamó con sorna: «¡Esa hormiga debe de estar ya a un montón de kilómetros de aquí!».)
En una secuencia de organismos cada vez menos sofisticados —pongamos un perro, un pez de colores, un gusano y una ameba— el aprendizaje individual tiene cada vez menos relevancia en comparación con los instintos acumulados en el transcurso de la evolución biológica. Pero la propia evolución biológica puede ser descrita a su vez como un sistema complejo adaptativo, incluso en los organismos más sencillos.