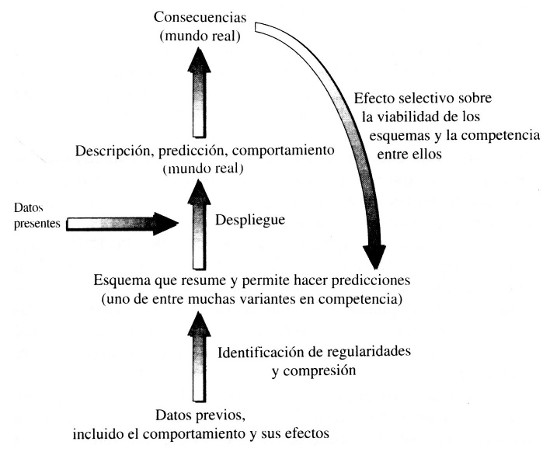
Figura 2. Funcionamiento de un sistema complejo adaptativo
Información y complejidad
El estudio de cualquier sistema complejo adaptativo se concentra en la información, que llega al sistema en forma de un flujo de datos (por ejemplo, una secuencia de imágenes, mostradas a un sujeto en un experimento psicológico). Examinamos la manera en que el sistema percibe regularidades que extrae del flujo de datos separándolas de lo que es incidental o arbitrario y condensándolas en un esquema sujeto a variación (en el supuesto anterior, el sujeto crea y modifica continuamente leyes hipotéticas que se supone que gobiernan las regularidades encontradas en la secuencia de imágenes). Observamos cómo cada uno de los esquemas resultantes se combina entonces con información adicional, de la clase de la información incidental dejada de lado en la abstracción de regularidades a partir del flujo de datos, para generar un resultado aplicable al mundo real: la descripción de un sistema observado, la predicción de algún suceso o la prescripción del comportamiento del propio sistema complejo adaptativo. (En el experimento psicológico, el sujeto puede combinar un posible esquema basado en las imágenes anteriores con unas cuantas de las siguientes para hacer una predicción de las imágenes que saldrán a continuación. En este caso, como suele pasar, la información adicional procede de una porción posterior del mismo flujo de datos del que el esquema fue abstraído.) Finalmente, vemos qué efectos tiene dicha descripción, predicción o comportamiento en el mundo real; tales efectos son retroactivos, ejerciendo «presiones selectivas» sobre los esquemas en competencia, algunos de los cuales quedan desacreditados o descartados, mientras que otros sobreviven y prosperan. (En el ejemplo, un esquema predictivo contradicho por las imágenes subsiguientes presumiblemente será descartado por el sujeto, mientras que otro cuyas predicciones son correctas será conservado. Aquí el esquema se pone a prueba contrastándolo con una porción ulterior del mismo flujo de datos del que nació y del que se obtuvo la información adicional para hacer predicciones.) El funcionamiento de un sistema complejo adaptativo puede representarse en un diagrama como el de esta página, donde se hace hincapié en el flujo de información.

Figura 2. Funcionamiento de un sistema complejo adaptativo
Los sistemas complejos adaptativos se hallan sujetos a las leyes de la naturaleza, que a su vez se fundamentan en las leyes físicas de la materia y el universo. Por otra parte, la existencia de tales sistemas sólo es posible en condiciones particulares.
Para examinar el universo y la estructura de la materia podemos seguir la misma estrategia adoptada en el estudio de los sistemas complejos adaptativos: concentrarse en la información. ¿Cuáles son las regularidades y dónde entran la contingencia y la arbitrariedad?
De acuerdo con la física decimonónica, el conocimiento exacto de las leyes del movimiento y de la configuración del universo en un momento dado permitiría, en principio, la predicción de la historia completa de éste. Ahora sabemos que esto es absolutamente falso. El universo es mecanocuántico, lo que implica que, aun conociendo su estado inicial y las leyes fundamentales de la materia, sólo puede calcularse un conjunto de probabilidades para las diferentes historias posibles. Por otra parte, esta «indeterminación» cuántica va mucho más allá de lo que suele creerse. Mucha gente conoce el principio de incertidumbre de Heisenberg, que prohíbe, por ejemplo, conocer simultáneamente con exactitud la posición y el momento de una partícula. Mientras que este principio ha sido ampliamente divulgado (a veces de manera francamente errónea) apenas se habla de la indeterminación adicional requerida por la mecánica cuántica. Más adelante volveremos sobre este tema.
Aunque la aproximación clásica esté justificada y, en consecuencia, pueda ignorarse la indeterminación mecanocuántica, todavía nos queda el extendido fenómeno del caos, en el que la evolución de un proceso dinámico no lineal es tan sensible a las condiciones iniciales que un cambio minúsculo en la situación al principio del proceso se traduce en una gran diferencia al final.
Algunas de las conclusiones contemporáneas sobre determinismo y caos en mecánica clásica ya fueron anticipados en 1903 por el matemático francés Henri Poincaré en su libro Ciencia y método (citamos por Ivars Peterson en Newton’s Clock [El reloj de Newton]):
«Si conociéramos con precisión infinita las leyes de la naturaleza y la situación inicial del universo, podríamos predecir exactamente la situación de este mismo universo en un momento posterior. Pero incluso aunque las leyes naturales no tuvieran ningún secreto para nosotros, sólo podríamos conocer la situación inicial de modo aproximado. Todo lo que necesitamos para poder decir que un fenómeno ha sido predicho y que está regido por leyes es poder predecir la situación posterior con la misma aproximación que la inicial. Pero esto no siempre es posible; puede ocurrir que las pequeñas diferencias en las condiciones iniciales se hagan muy grandes en el resultado final. Un pequeño error al principio producirá un error enorme al final. La predicción se hace imposible y tenemos un fenómeno fortuito.»
Uno de los artículos que llamaron la atención sobre el caos en los años sesenta fue publicado por el meteorólogo Edward N. Lorenz. De hecho, la meteorología es una fuente de ejemplos familiares de caos. Aunque las fotografías por satélite y el uso de potentes ordenadores han hecho que la predicción del tiempo sea absolutamente fiable para muchos propósitos, los partes meteorológicos todavía no pueden garantizarnos lo que mucha gente quiere saber: si lloverá o no aquí y mañana. Tanto el lugar exacto por donde pasará una tormenta como el momento en que descargará la lluvia pueden ser arbitrariamente sensibles a los detalles de los vientos y de la posición y estado físico de las nubes unos cuantos días o incluso unas horas antes. La más ligera imprecisión en los datos meteorológicos hace que uno no pueda fiarse de la previsión para mañana a la hora de planear una excursión.
Dado que nada puede medirse con una precisión absoluta, el caos da origen a una indeterminación efectiva en el nivel clásico que se superpone a la indeterminación cuántica. La interacción entre estas dos clases de impredictibilidad es un aspecto fascinante y todavía poco estudiado de la física contemporánea. El reto que supone comprender la relación entre la impredictibilidad de carácter cuántico y la de carácter caótico ha llegado incluso a llamar la atención de los editores de Los Angeles Times, tanto que en 1987 le dedicaron al tema un editorial en el que se señalaba la aparentemente paradójica incapacidad de los teóricos para encontrar la indeterminación de carácter caótico que debería aparecer superpuesta a la de carácter cuántico cuando se aplica la mecánica cuántica a sistemas que exhiben caos en el dominio clásico.
Pero la cuestión comienza a aclararse gracias al trabajo de diversos físicos teóricos, entre ellos Todd Brun, uno de mis discípulos. Sus resultados parecen indicar que, para muchos propósitos, es útil contemplar el caos como un mecanismo que amplifica a escala macroscópica la indeterminación inherente a la mecánica cuántica.
En los últimos tiempos se ha publicado un montón de artículos sobre caos escritos bastante a la ligera. Un término técnico, aplicado en principio a un fenómeno de la mecánica no lineal, ha acabado convirtiéndose en una especie de etiqueta para designar cualquier clase de complejidad o incertidumbre, real o aparente. Si en alguna de mis conferencias sobre, digamos, sistemas complejos adaptativos, menciono el fenómeno aunque sólo sea una vez, y a veces ni eso, estoy seguro de que seré felicitado al final por mi interesante charla sobre «caos».
El impacto de los descubrimientos científicos en la literatura y la cultura popular tiende a traducirse en que ciertos elementos de vocabulario, interpretados de modo vago o erróneo, suelen ser lo único que sobrevive al viaje desde la publicación técnica a los libros y revistas populares. Los dominios de aplicación o las distinciones importantes, y a veces las propias ideas, tienden a perderse por el camino. Piénsese si no en los usos populares de palabras como «ecología» o «salto cuántico», y ya no digamos de la expresión New Age «campo de energía». Naturalmente, uno siempre puede argumentar que palabras como «caos» o «energía» ya existían antes de convertirse en términos técnicos, pero lo que resulta distorsionado en el proceso de vulgarización es precisamente su significado técnico, no el original.
Dada la eficacia creciente de las técnicas literarias en la transformación de conceptos útiles en tópicos huecos, hay que esmerarse si se quiere evitar que las diversas nociones de complejidad corran la misma suerte. Más adelante las detallaremos y examinaremos el dominio de aplicación de cada una de ellas.
Pero antes, ¿qué se entiende por «complejo» cuando hablamos de «sistema complejo adaptativo» en el sentido aquí empleado? De hecho, no hace falta que la palabra «complejo» tenga un significado preciso en esta frase, que es puramente convencional. Su presencia implica la convicción de que tales sistemas poseen un grado mínimo de complejidad convenientemente definido.
La simplicidad hace referencia a la ausencia (o casi) de complejidad. Etimológicamente, simplicidad significa «plegado una vez», mientras que complejidad significa «todo trenzado» (nótese que tanto «plic-» para pliegue como «plej-» para trenza derivan de la misma raíz indoeuropea plek).
¿Qué se entiende realmente por simplicidad y complejidad? ¿En qué sentido es simple la gravitación einsteniana y complejo un pez de colores? No son cuestiones sencillas —no es simple definir «simple»—. Probablemente no existe un único concepto de complejidad que pueda captar adecuadamente nuestras nociones intuitivas. Puede que se requieran varias definiciones diferentes, algunas quizá todavía por concebir.
Una definición de complejidad surge de la ciencia informática, y tiene que ver con el tiempo requerido por un ordenador para resolver un problema determinado. Dado que este tiempo depende también de la competencia del programador, el que se toma en consideración es el más corto posible, lo que se conoce habitualmente como «complejidad computacional» del problema.
Dicho tiempo mínimo depende aún de la elección del ordenador. Esta «dependencia del contexto» surge una y otra vez en los intentos de definición de complejidad. Pero los informáticos se interesan particularmente en conjuntos de problemas que son similares excepto en magnitud, y por lo tanto la cuestión principal es saber qué pasa con la complejidad computacional cuando la magnitud del problema aumenta ilimitadamente. ¿Cuál es la relación entre el tiempo mínimo y la magnitud del problema cuando ésta tiende a infinito? La respuesta a esta cuestión puede que sea independiente de los detalles del ordenador.
La complejidad computacional ha demostrado ser una noción verdaderamente útil, pero no se corresponde demasiado con el sentido habitual de la palabra «complejo», como cuando se dice que el argumento de un relato o la estructura de una organización son altamente complejos. En este contexto estamos más interesados en saber cuán largo sería el mensaje requerido para describir determinadas propiedades del sistema en cuestión que en saber cuánto se tardaría en resolver cierto problema con un ordenador.
En el seno de la ecología se ha debatido durante décadas si los sistemas «complejos», como las selvas tropicales, tienen un poder de recuperación mayor o menor que los sistemas comparativamente «simples», como los bosques alpinos de robles y coníferas. Aquí el poder de recuperación se refiere a la probabilidad de sobrevivir a (o incluso sacar partido de) perturbaciones tales como cambios climáticos, incendios u otras alteraciones del medio ambiente, hayan sido o no causadas por la actividad humana. Parece ser que entre los ecólogos se va imponiendo el argumento de que, hasta cierto punto, el ecosistema más complejo es el más resistente. ¿Pero qué se entiende aquí por simple y complejo? La respuesta tiene que ver ciertamente con la longitud de la descripción del bosque.
Una noción muy elemental de la complejidad de un bosque podría obtenerse contando el número de especies de árboles (menos de una docena en un bosque alpino típico de clima templado frente a cientos de ellas en una selva tropical). También se podría contar el número de especies de aves y mamíferos; otra vez saldrían ganando las selvas tropicales. Con los insectos las diferencias serían aún mayores —piénsese en el número de especies de insectos que debe de haber en la selva ecuatorial—. (Siempre se ha creído que este número debía de ser muy grande, pero las estimaciones recientes sugieren que es todavía más grande de lo que se pensaba. A partir de los estudios de Terry Erwin, de la Smithsonian Institution, consistentes en recoger y clasificar todos los insectos presentes en un solo árbol tropical, se ha visto que el número de especies, muchas de ellas nuevas para la ciencia, es del orden de diez veces mayor de lo que se suponía.)
También se pueden tomar en consideración las interacciones entre organismos, del tipo depredador-presa, parásito-huésped, polinizador-polinizado, etc.
Ahora bien, ¿con qué detalle habría que hacer las observaciones? ¿Habría que considerar los microorganismos, virus incluidos? ¿Habría que atender a las interacciones más sutiles además de las obvias? Está claro que hay que detenerse en algún punto.
Por lo tanto, cuando se define una forma de complejidad siempre es necesario acotar el grado de detalle en la descripción del sistema, ignorando los detalles más finos. Los físicos llaman a esto «resolución». Piénsese en una imagen fotográfica. Si se amplía algún pequeño detalle de la misma se pondrán de manifiesto los gránulos individuales de la película y se verá sólo un montón de puntos que componen una imagen tosca del detalle observado. El título de la película de Antonioni Blow-Up se refiere a esa ampliación. El granulado de la fotografía impone un límite en la cantidad de información que puede proporcionar ésta. Si la película es de grano muy grueso, lo más que puede obtenerse es una imagen de baja resolución que da una impresión aproximada de lo fotografiado. Si un satélite espía fotografía un «complejo» militar desconocido con anterioridad, la medida de complejidad que se le asigne dependerá también del granulado de la película.
Una vez establecida la importancia de la resolución, aún queda pendiente la cuestión de cómo definir la complejidad de lo que se observa. ¿Qué caracteriza, por ejemplo, una red de comunicación compleja entre un cierto número (digamos N) de personas? Esta cuestión podría planteársele a un psicólogo o sociólogo que intente comparar lo bien o lo rápido que es resuelto un problema por las N personas en diferentes condiciones de comunicación. En un extremo (que llamaremos caso A) cada persona trabaja por su cuenta y no existe ninguna comunicación. En el otro (que llamaremos caso F) cada persona puede comunicarse con cualquier otra. El caso A es obviamente simple, pero ¿es el caso F mucho más complejo o es de una simplicidad comparable a la del caso A?
Para fijar el grado de detalle (resolución) supongamos que cada persona recibe un tratamiento equivalente, sin distinción de rasgos individuales, y es representada en un diagrama como un simple punto en posición arbitraria, siendo todos los puntos intercambiables. La comunicación entre dos personas cualesquiera es posible o imposible, sin gradaciones, y cuando existe se representa como un segmento (no orientado) que conecta dos puntos. El resultado es lo que los matemáticos llaman un «grafo no orientado».
Con el nivel de detalle así especificado puede explorarse el significado de la complejidad de un esquema de conexiones. Consideremos primero un pequeño número de puntos, por ejemplo ocho (N = 8). Es fácil entonces trazar parte de los esquemas que resultan, incluyendo algunos triviales. Los diagramas de la Figura 3 representan algunos de los esquemas de conexiones posibles entre ocho individuos. En A ningún punto está conectado con otro. En B hay puntos conectados y puntos aislados. En C todos los puntos están conectados, pero no aparecen todas las conexiones posibles. En D aparecen las conexiones que faltan en C y están ausentes las otras; D es lo que podríamos llamar el «complementario» de C y viceversa. Lo mismo podemos decir de E y B, y también de F y A: en el esquema A no hay conexiones, mientras que en el F están todas las posibles. ¿A qué esquemas hay que asignar mayor, o menor, complejidad?
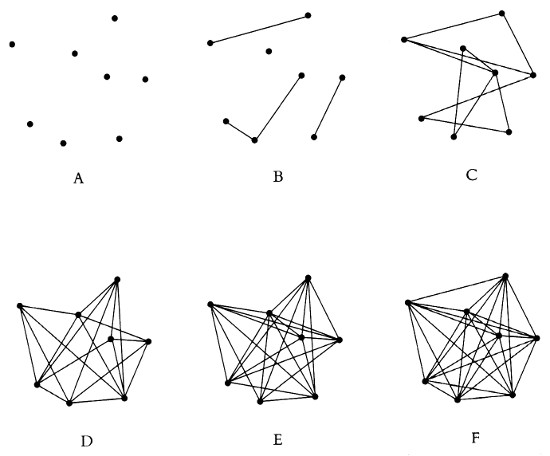
Figura 3. Algunos esquemas de conexiones posibles entre ocho puntos
Todo el mundo estará de acuerdo en que A, que no tiene conexiones, es simple y que B, con algunas conexiones, es más complejo, o menos simple, que A. Pero ¿qué ocurre con el resto? El caso F es particularmente interesante. Inicialmente, uno podría pensar que se trata del más complejo de todos, pues es donde hay más conexiones. Ahora bien, ¿es esto razonable? ¿No resulta acaso igual de simple estar totalmente conectado que no estarlo en absoluto? Quizá F deba situarse junto con A en la parte inferior de la escala de complejidad.
Lo cual nos lleva de nuevo a la propuesta de definir la complejidad de un sistema por medio de la longitud de su descripción. La figura F resulta entonces tan simple como su complementaria A, ya que la frase «todos los puntos conectados» es más o menos igual de larga que la frase «ningún punto conectado». Por otra parte, la complejidad de E no es muy diferente de la de su complementario B, ya que la adición del término «complementario» no alarga significativamente la descripción. Lo mismo pasa con D y C. En general, los esquemas complementarios tendrán una complejidad semejante.
Los esquemas B y E son evidentemente más complejos que A y F, y lo mismo pasa con C y D. La comparación de B y E con C y D es más complicada. Según el criterio de la longitud de la descripción, podría parecer que C y D son más complejos, pero el que esto sea cierto depende en alguna medida del vocabulario disponible para efectuar la descripción.
Antes de seguir adelante, es interesante remarcar que los mismos diagramas y la misma argumentación que hemos desarrollado en relación con los esquemas de comunicación pueden aplicarse a otra situación de gran trascendencia para la ciencia, la tecnología y el comercio actuales. La informática moderna está haciendo rápidos progresos en la construcción y utilización de ordenadores «paralelos», mucho más efectivos que las máquinas convencionales en la resolución de ciertos problemas. En lugar de un único ordenador gigante que trabaja continuamente en un problema hasta su conclusión, se disponen numerosas unidades más pequeñas trabajando simultáneamente, con una determinada red de conexiones entre ellas. Una vez más podemos preguntamos qué significado tiene el que una red de comunicación sea más compleja que otra. De hecho, fue precisamente un físico que trabajaba en el diseño de un ordenador paralelo quien me planteó esta misma cuestión hace años, renovando así mi interés en el problema de la definición de la complejidad.
Recordemos la posibilidad de contar el número de especies, tener en cuenta las interacciones, etc., como opción para caracterizar las comunidades ecológicas simples y complejas. Si se hiciera una lista de, por ejemplo, los tipos de árboles presentes en una comunidad, la longitud de esta parte de la descripción sería más o menos proporcional al número de especies de árboles. También en este caso, por lo tanto, sería de hecho la longitud de la descripción lo que se estaría empleando como medida.
Si la complejidad se define en términos de la longitud de una descripción dada, entonces no es una propiedad intrínseca de la cosa descrita. Es obvio que la longitud de la descripción depende también del descriptor. (Me viene a la memoria el relato de James Thurber «The Glass in the Field» [El cristal en el campo], en el que un jilguero cuenta a los otros pájaros su colisión con una lámina de vidrio: «Volaba cruzando un prado cuando de pronto el aire cristalizó sobre mí».) Cualquier definición de complejidad es necesariamente dependiente del contexto, incluso subjetiva. El grado de detalle con que se efectúa la descripción del sistema tiene ya algo de subjetivo —también depende del observador o de los instrumentos de observación—. Así pues, en realidad estamos discutiendo una o más definiciones de complejidad que dependen de la descripción del sistema a cargo de otro sistema, presumiblemente un sistema complejo adaptativo que podría ser un observador humano.
Para precisar la noción de longitud de una descripción hay que eliminar la posibilidad de describir algo simplemente señalándolo, pues es tan fácil señalar un sistema complejo como uno simple. La descripción del sistema debe suponerse dirigida a un interlocutor lejano. También es fácil dar un nombre como «Sam» o «Judy» a algo extremadamente complicado, haciendo su descripción trivialmente corta. Hay que describir el sistema mediante un lenguaje previamente convenido y que no incluya términos especiales introducidos a propósito.
Aun así quedan muchas fuentes de arbitrariedad y subjetividad. La longitud de la descripción dependerá del lenguaje empleado y también del conocimiento o concepción del mundo que compartan los interlocutores. La descripción de un rinoceronte, por ejemplo, puede acortarse si ambos interlocutores ya saben lo que es un mamífero. La descripción de la órbita de un asteroide es muy diferente si los interlocutores conocen la ley de gravitación de Newton y su segunda ley del movimiento —también puede influir en la longitud de la descripción el hecho de que ambas partes conozcan las órbitas de Marte, Júpiter y la Tierra.
Pero ¿qué pasa cuando la descripción se hace innecesariamente larga? Es como la historia del maestro que puso como deber a sus alumnos escribir una redacción de trescientas palabras. Uno de ellos, que se había pasado todo el tiempo jugando, a última hora garabateó lo siguiente: «Ayer tarde a los vecinos se les incendió la cocina y yo saqué la cabeza por la ventana y grité: “¡Fuego! ¡Fuego! ¡Fuego!…”». Así hasta completar las trescientas palabras exigidas. Sin embargo, de no haber sido por este requerimiento, podría perfectamente haber escrito «… grité “¡fuego!” doscientas ochenta veces» para comunicar lo mismo. Está claro que en nuestra definición de complejidad debemos referimos siempre a la longitud del mensaje más corto posible para describir el sistema.
Todos estos puntos pueden integrarse en una definición de lo que podría llamarse «complejidad bruta»: la longitud del mensaje más corto que describe un sistema, con una resolución dada, dirigido a un interlocutor distante y haciendo uso de un lenguaje y un conocimiento del mundo que ambas partes comparten (y saben que comparten) de antemano.
Algunas maneras familiares de describir un sistema no dan como resultado nada parecido al mensaje más corto. Por ejemplo, si describimos por separado las partes de un sistema (como las piezas de un coche o las células de un ser humano) junto con el modo en que se ensamblan entre sí, estamos ignorando muchas formas de comprimir el mensaje que harían uso de las similaridades entre las partes. Casi todas las células del cuerpo humano, por ejemplo, comparten los mismos genes, además de muchos otros rasgos comunes, y las células de un tejido cualquiera son incluso más similares. La descripción más corta debería tenerlo en cuenta.
Algunos expertos en teoría de la información hacen uso de una magnitud muy parecida a la complejidad bruta, aunque de definición más técnica y, naturalmente, relacionada con los ordenadores. Se parte de una descripción con una resolución dada y expresada en un lenguaje determinado, que es codificada en una cadena de ceros y unos por medio de algún procedimiento de codificación estándar. Cada elección de un 1 o un 0 es un «bit» (contracción de binary digit, «dígito binario» en inglés; binario porque sólo hay dos elecciones posibles, mientras que en el sistema decimal normal hay diez, los dígitos 0, 1,2, 3, 4, 5, 6, 7, 8, 9). Lo que se maneja es una cadena de bits, o «mensaje codificado».
La magnitud definida recibe el nombre de «complejidad algorítmica», «contenido de información algorítmica» o «incertidumbre algorítmica». La palabra «algoritmo» se refiere a una regla para calcular algo y también, por extensión, a un programa de ordenador. El contenido de información algorítmica se refiere, como veremos, a la longitud de un programa de ordenador.
El significado original de algoritmo es algo diferente. Aunque suena parecido a «aritmética», que deriva del griego, en realidad la «t» se introdujo por analogía, y quizá sería más correcto decir «algorismo», que refleja mejor la etimología. La palabra deriva del nombre de un matemático árabe del siglo IX, Mohamed ben Musa al Khuarizmi, que fue quien introdujo el concepto de cero en la cultura occidental. El apellido indica que su familia procedía de la provincia de Khorezm, al sur del mar de Aral, dentro de la república ahora independiente de Uzbekistán. Escribió un tratado en cuyo título aparece la frase al jabr («la transposición» en árabe), de la que deriva la palabra «álgebra». Originalmente, la palabra «algorismo» hacía referencia al sistema decimal de numeración, que se cree llegó a Europa desde la India principalmente a través de la traducción al latín del «Algebra» de al Khuarizmi.
El contenido de información algorítmica fue introducido por tres autores, de modo independiente, en los años sesenta. Uno fue el gran matemático ruso Andréi N. Kolmogorov. Otro fue el norteamericano Gregory Chaitin, que a la sazón contaba sólo quince años. El tercero fue otro norteamericano, Ray Solomonoff. Todos suponen la existencia de un ordenador ideal, de memoria infinita (o finita pero ampliable) y equipado con circuitos y programas predeterminados. Después consideran un mensaje codificado particular y los programas que hacen que el ordenador imprima el mensaje y después se pare. La longitud del más corto de tales programas es el contenido de información algorítmica del mensaje.
Hemos visto que existe una subjetividad o arbitrariedad inherente a la definición de complejidad bruta, que surge de fuentes como la resolución y el lenguaje empleado en la descripción del sistema. En el contenido de información algorítmica se introducen nuevas fuentes de arbitrariedad, a saber, el procedimiento de codificación particular que convierte la descripción del sistema en una cadena de bits, y los circuitos y programas particulares del ordenador.
Ninguna de estas fuentes de arbitrariedad incomoda demasiado a los matemáticos, que suelen moverse dentro de límites en los que la arbitrariedad finita se hace comparativamente insignificante. Acostumbran a considerar series de cadenas de bits similares y de longitud creciente, estudiando cómo se comporta el contenido de información algorítmica cuando la longitud tiende a infinito (lo que recuerda el tratamiento de la complejidad computacional de una serie de problemas similares a medida que el problema se hace infinitamente grande).
Volvamos al ordenador paralelo ideal compuesto de unidades, representadas por puntos, conectadas por enlaces de comunicación representados por líneas. Aquí Kolmogorov, Chaitin y Solomonoff no se interesarían demasiado por el contenido de información algorítmica de los diversos esquemas de conexiones entre ocho puntos en concreto, sino que se interrogarían sobre las conexiones entre N puntos cuando N tiende a infinito. En estas condiciones, ciertas diferencias en el comportamiento del contenido de información algorítmica (por ejemplo entre el esquema de conexiones más simple y el más complejo) hacen insignificantes las diferencias atribuibles al ordenador, el procedimiento de codificación e incluso el lenguaje de turno. Los teóricos de la información se interesan en si un cierto contenido de información algorítmica sigue aumentando a medida que N se aproxima a infinito y, si lo hace, a qué ritmo. No se preocupan demasiado por las diferencias, en comparación despreciables, en el contenido de información algorítmica introducidas por las diversas fuentes de arbitrariedad en el aparato descriptivo.
De todos estos estudios teóricos se puede extraer una interesante conclusión. Aunque no nos restrinjamos a sistemas que se hacen infinitamente grandes, es importante comprender que las discusiones sobre simplicidad y complejidad adquieren más sentido a medida que las cadenas de bits se hacen más largas. En el otro extremo, para una cadena de un solo bit, es evidente que no tiene sentido hablar de simplicidad y complejidad.
Es momento de dejar clara la distinción entre información algorítmica e información tal como la concibe, por ejemplo, Claude Shannon, el fundador de la moderna teoría de la información. Básicamente, la información tiene que ver con una selección entre diversas alternativas, y puede expresarse de modo muy simple si dichas alternativas pueden reducirse a una serie de elecciones entre alternativas binarias igualmente probables. Por ejemplo, si sabemos que el resultado de lanzar una moneda ha sido cruz en vez de cara, tenemos un bit de información. Si sabemos que el resultado de lanzar una moneda tres veces ha sido cara, cruz y cara, tenemos tres bits de información.
El juego de las veinte preguntas proporciona una bonita ilustración de las más diversas clases de información en la forma de elecciones sucesivas entre alternativas binarias igualmente probables, o tan cerca de la equiprobabilidad como el interrogador pueda conseguir. Se juega entre dos personas, una de las cuales piensa algo que la otra tiene que adivinar con veinte preguntas o menos, después de averiguar si es animal, vegetal o mineral. Las cuestiones sólo pueden responderse con un «sí» o un «no»; cada una es una alternativa binaria. Para el segundo jugador es ventajoso que sus preguntas le permitan acercarse todo lo posible a una elección entre alternativas igualmente probables. Sabiendo que la cosa es, por ejemplo, un mineral, no sería aconsejable que el interrogador preguntara directamente si se trata del diamante Esperanza. En vez de eso, podría preguntar algo así como «¿es natural?» (en oposición a manufacturado o tratado por manos humanas). Aquí la probabilidad de una respuesta afirmativa es más o menos igual a la de una respuesta negativa. Si la respuesta es «no», la siguiente cuestión podría ser «¿es un objeto concreto?» (en oposición a una clase de objetos). Cuando las probabilidades de una respuesta positiva o negativa son iguales, cada pregunta rinde un bit de información. Veinte bits de información corresponden a una elección entre 1 048 576 alternativas equiprobables, el producto de la multiplicación de 20 factores de 2 (este producto es el número de cadenas de bits diferentes de longitud 20).
Nótese que en el tratamiento del contenido de información algorítmica las cadenas de bits se emplean de modo diferente que en el de la información de Shannon. En el caso del contenido de información algorítmica se considera una cadena de bits (preferiblemente larga) y se miden sus regularidades internas mediante la longitud (en bits) del programa más corto que hará que un ordenador estándar la imprima y después se pare. En contraste, en el caso de la información uno puede considerar una elección entre todas las diferentes cadenas de bits de una longitud dada. Si todas son igualmente probables, su longitud es el número de bits de información.
Uno puede tratar también con un conjunto de cadenas de bits, que pueden ser igualmente probables, cada una con un contenido de información algorítmica particular. En ese caso es útil definir el promedio de la cantidad de información y también el promedio del contenido de información algorítmica, ambos determinados por el número de cadenas de bits.
El contenido de información algorítmica tiene una propiedad muy curiosa. Para discutirla tenemos que fijamos en primer lugar en la «compresibilidad» relativa de diferentes mensajes. Para una cadena de bits de cierta longitud (digamos una muy larga) podemos preguntamos cuándo la complejidad algorítmica es baja y cuándo es alta. Si una cadena larga tiene la forma 110110110110110110110 …110110, puede ser producida por un programa muy corto que imprima 110 un número determinado de veces. Esta cadena de bits tiene un contenido de información algorítmica muy bajo aunque sea larga. Esto quiere decir que es altamente compresible.
En contraste, puede demostrarse matemáticamente que la mayoría de cadenas de bits de una cierta longitud son incompresibles. En otras palabras, el programa más corto capaz de producirlas (y después detener el ordenador) es aquel que dice IMPRIMIR seguido de la cadena misma. Las cadenas de bits de esta clase tienen un contenido de información algorítmica máximo para una longitud dada. No hay ninguna regla, ni algoritmo, ni teorema que simplifique la descripción de la cadena y permita describirla con un mensaje más corto. Se les llama «aleatorias» precisamente porque no contienen regularidades que permitan comprimirlas. El hecho de que el contenido de información algorítmica sea máximo para las cadenas aleatorias justifica la denominación alternativa de incertidumbre algorítmica.
Una curiosa propiedad de la información algorítmica es que no es computable. Aunque la mayoría de cadenas de bits es aleatoria, no hay manera de conocer exactamente cuándo lo son. De hecho, en general no puede asegurarse que el contenido de información algorítmica de una cadena dada no sea menor de lo que pensamos. Esto se debe a que siempre puede haber un teorema que nunca encontraremos o un algoritmo que nunca descubriremos que permitiría comprimir la cadena de bits. De modo más preciso, no existe un procedimiento para encontrar todos los teoremas que permitirían una ulterior compresión. Esto fue demostrado hace unos años por Greg Chaitin, en un trabajo con reminiscencias de un famoso resultado de Kurt Gödel.
Gödel fue un lógico matemático que, a principios de la década de los treinta, dejó aturdidos a sus colegas con sus descubrimientos sobre las limitaciones de los sistemas de axiomas en matemáticas. Hasta entonces, los matemáticos creían posible formular un sistema de axiomas que demostrase ser consistente y del que, en principio, pudiese derivarse la verdad o falsedad de todas las proposiciones matemáticas. Gödel demostró que ninguna de estas metas es alcanzable.
Estas conclusiones negativas suponen un progreso monumental tanto en matemáticas como en la ciencia en general. Pueden compararse con el descubrimiento de Albert Einstein de que no es posible definir un tiempo o espacio absolutos, sino sólo un espacio-tiempo que sea combinación de ambos. De hecho, Gödel y Einstein eran buenos amigos. A principios de los cincuenta solía verlos paseando juntos en el Instituto de Estudios Avanzados de Princeton, en New Jersey. Formaban una curiosa pareja. Gödel era tan bajito que a su lado Einstein parecía alto. Nunca supe si discutían sobre cuestiones profundas de matemáticas o de física (Gödel trabajaba de vez en cuando en problemas de relatividad general) o del tiempo y de sus problemas de salud.
De entre las conclusiones de Gödel, las más relevantes para nuestra discusión son las relativas a la indecidibilidad: dado un sistema de axiomas matemáticos, siempre habrá proposiciones indecidibles sobre la base de tales axiomas. En otras palabras, hay proposiciones de las que, en principio, no puede demostrarse su verdad o falsedad.
Las proposiciones indecidibles más celebradas son aquellas que son independientes de los axiomas. Cuando se tiene una de tales proposiciones, el conjunto inicial de axiomas puede ampliarse introduciéndola como nuevo axioma, y lo mismo puede hacerse con la proposición contraria.
Pero hay otras proposiciones indecidibles de carácter distinto. Supongamos, por ejemplo, una proposición indecidible relativa a los enteros positivos de la forma «todo número par mayor que 2 tiene la propiedad siguiente…». En principio, si hubiese alguna excepción a tal proposición podríamos encontrarla, al cabo de un cierto tiempo, probando un número par tras otro (4, 6, 8, 10, …) hasta dar con uno que contradiga el enunciado. Esto demostraría inmediatamente la falsedad de la proposición, pero también contradiría su indecidibilidad, pues indecidible quiere decir precisamente que no puede demostrarse si la proposición es verdadera o falsa. Por lo tanto, no puede haber excepciones. La proposición es «verdadera» en el sentido ordinario de la palabra.
Podemos concretar la cuestión considerando una proposición que, tras siglos de esfuerzos, nunca ha sido demostrada, aunque no se ha encontrado ninguna excepción que la refute. Se trata de la conjetura de Goldbach, que establece que todo número par mayor que 2 resulta de la suma de dos números primos (iguales o distintos). Un número primo es un número mayor que 1 que no es divisible por ningún número excepto él mismo y 1. Los primeros son 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 y 37. Es fácil ver que cualquier número par entre 4 y 62 puede expresarse al menos de una manera como suma de dos elementos de esta lista. Con el empleo de ordenadores se ha podido verificar esta propiedad hasta números pares increíblemente grandes. Sin embargo, ningún ordenador puede demostrar la conjetura, que siempre podría dejar de ser cierta para algún número aún más grande. Sólo una demostración matemática rigurosa podría convertir la conjetura en un teorema cierto.
No hay razón para pensar que la conjetura de Goldbach sea indecidible, pero supongamos que lo fuera. Entonces, aunque indemostrable, sería verdadera, pues no podría haber ninguna excepción a ella. La existencia de cualquier número par mayor que 2 que no fuera la suma de dos primos refutaría la conjetura, lo que contradiría su indecidibilidad.
La existencia oculta de tales teoremas verdaderos pero indemostrables significa, como Chaitin ha demostrado, que siempre puede haber uno que permita comprimir un mensaje largo cuando pensamos que es incompresible, o comprimirlo más cuando creemos haber encontrado el programa de ordenador más corto que hará imprimir el mensaje y parar. Así pues, en general no se puede estar seguro del contenido de información algorítmica; sólo puede establecerse un límite superior, un valor que no puede excederse. Dado que el valor real podría estar por debajo de este límite, el contenido de información algorítmica no es computable.
La no computabilidad es una propiedad que puede crear problemas, pero lo que en verdad impide que el contenido de información algorítmica pueda emplearse para definir la complejidad es otra cosa. El contenido de información algorítmica es útil para la introducción de nociones como resolución, compresibilidad o cadena de bits, así como la de longitud de una descripción generada por un sistema observador, pero su nombre alternativo de incertidumbre algorítmica delata un importante defecto. El contenido de información algorítmica es mayor para las cadenas aleatorias. Es una medida de incertidumbre, que no es lo que suele entenderse por complejidad, ni en sentido ordinario ni en sentido más científico. Así pues, el contenido de información algorítmica no representa una complejidad verdadera o efectiva.
En cualquier discusión sobre incertidumbre hay que ser cuidadoso, pues el término no siempre significa exactamente lo mismo. Reparé en este escollo por primera vez hace tiempo, en mis contactos con la RAND Corporation.