Aquiles y la Tortuga han venido a la residencia de su amigo el Cangrejo para conocer a uno de sus amigos, el Oso Hormiguero. Hechas las presentaciones, los cuatro se disponen a tomar el té.

Tortuga: Hemos traído con nosotros un pequeño regalo para Ud., Sr. Cangrejo.

Cangrejo: Eso es muy amable por su parte. Pero no deberían haberse molestado.

Tortuga: Es sólo una muestra de nuestra estima. Aquiles, ¿querría entregárselo al Sr. C?

(Aquiles le extiende al Cangrejo un presente elegantemente envuelto; cuadrado y muy delgado. El Cangrejo comienza a desenvolverlo.)

Cangrejo: Pronto lo averiguaremos. (Termina de desenvolverlo y saca el regalo.) ¡Dos discos! ¡Qué excitante! Pero no tienen etiqueta. Uh-oh —¿es éste otro de sus “especiales”, Sr. T?

Tortuga: Si se refiere a un rompefonógrafos, no esta vez. Pero, de hecho, es un ítem grabado a pedido, el único de su especie en el mundo entero. En realidad, nunca ha sido escuchado antes —excepto, por supuesto, cuando Bach lo tocó.

Aquiles: Oh, Ud. va a estar emocionadísimo, Sr. Cangrejo, cuando el Sr. T le cuente lo que efectivamente son estos discos.

Aquiles: ¿Me permite? ¡Oh, caramba! Entonces será mejor que consulte mis notas. (Saca una pequeña ficha y despeja su voz.) Ejem. ¿Estaría interesado en escuchar acerca de los notables nuevos resultados en matemáticas a los que sus discos deben su existencia?

Cangrejo: ¿Mis discos se derivan de algún fragmento de las matemáticas? ¡Qué curioso! Bueno, ahora que ha provocado mi curiosidad, no me queda más remedio que escuchar acerca de ello.

Aquiles: Muy bien, entonces. (Hace una pausa para tomar un sorbo de té, y luego continúa.) ¿Han oído hablar acerca del infame “Teorema Final” de Fermat?

Oso Hormiguero: No estoy seguro… Me suena curiosamente familiar y, sin embargo, no lo sitúo bien.

Aquiles: Se trata de una idea sumamente simple. Pierre de Fermat, abogado formidable por vocación, pero formidable matemático por advocación, estaba leyendo su ejemplar del texto clásico Arithmetica de Diofanto cuando dio con una página que contenía la ecuación:

Inmediatamente comprendió que esta ecuación tiene infinitas soluciones para a, b, c, y entonces escribió en el margen el siguiente notable comentario:

La ecuación

aⁿ + bⁿ = cⁿ

tiene soluciones para enteros positivos a, b, c y n sólo cuando n = 2 (y entonces hay infinitos trípletes a, b, c que satisfacen la ecuación); pero no hay soluciones para n > 2. He descubierto una demostración verdaderamente maravillosa de este postulado, pero, desafortunadamente, este margen es demasiado pequeño para contenerla.

Desde aquel día, hace unos trescientos años la comunidad de matemáticos ha tratado en vano de hacer ya sea una de dos cosas: o probar la proclama de Fermat y reivindicar así la reputación de Fermat que, aunque muy grande, ha sido un tanto empañada por los escépticos que piensan que él nunca halló la demostración que reclamaba haber hallado —o bien refutar la proclama hallando un contraejemplo: una serie de cuatro enteros a, b, c y n, con n > 2, que satisfaga la ecuación. Hasta ahora, cada intento en una u otra dirección ha fracasado. Por cierto, el Teorema ha sido verificado para muchos valores específicos de n —en particular, todo n hasta 125.000.

Oso Hormiguero: ¿No debería ser llamado una “Conjetura” más que un “Teorema”, puesto que nunca ha sido adecuadamente demostrado?

Aquiles: Estrictamente hablando, tiene Ud. razón, pero la tradición lo ha mantenido así.

Cangrejo: ¿No hay nadie que finalmente se las haya arreglado para resolver este famoso problema?

Aquiles: ¡Por cierto! De hecho, el Sr. Tortuga lo ha hecho, y como es usual, mediante un golpe mágico. No sólo ha hallado una DEMOSTRACIÓN del Teorema Final de Fermat (justificando de este modo su nombre, así como reivindicando a Fermat), sino también un CONTRAEJEMPLO, ¡mostrando así que los escépticos tenían buenas intuiciones!

Oso Hormiguero: Pero por favor no nos deje en suspenso. ¿Qué enteros mágicos son esos que satisfacen la ecuación de Fermat? Tengo especial curiosidad acerca del valor de n.

FIGURA 55. Pierre de Fermat.

Aquiles: Oh, ¡qué horror! ¡Ahora sí que estoy en apuros! ¿Pueden creer esto? Dejé los valores en casa en un pedazo de papel verdaderamente colosal. Desafortunadamente era demasiado grande para traerlo conmigo. Desearía tenerlos aquí para mostrárselos a Uds. Si es que les sirve de ayuda, sí recuerdo una cosa —el valor de n es el único entero positivo que no aparece en ninguna parte en la fracción continua de π.

Cangrejo: Oh, qué lástima que no los tenga aquí. Pero no hay razón para dudar de lo que nos ha contado.

Oso Hormiguero: De cualquier forma, ¿quién necesita ver a n escrito en decimales? Aquiles nos acaba de decir cómo hallarlo. Bueno, Sr. T, por favor acepte mis felicitaciones de todo corazón con ocasión de su descubrimiento que hará época.

Tortuga: Gracias. Pero lo que me parece más importante que el resultado en sí mismo es el uso práctico al que inmediatamente condujo mi resultado.

Cangrejo: Me muero por oír acerca de ello, ya que siempre pensé que la teoría de los números era la Reina de las Matemáticas —la más pura rama de las matemáticas— ¡la rama de las matemáticas que NO tenía aplicaciones!

Tortuga: No es Ud. el único que cree eso, pero de hecho es completamente imposible hacer un postulado general acerca de cuándo o cómo una rama —o algún Teorema individual— de las matemáticas puras va a tener repercusiones importantes fuera de las matemáticas. Es completamente impredicible, y este caso es un ejemplo perfecto de este fenómeno.

Aquiles: ¡El re-sonante doble resultado del Sr. Tortuga ha abierto una aguda brecha en el concierto de la recuperación-acústica!

Aquiles: El nombre lo dice todo: es la recuperación de información acústica de fuentes extremadamente complejas. Una tarea típica de la recuperación-acústica es reconstruir el sonido que produjo una roca al desplomarse en un lago a partir de las olitas que se propagan sobre la superficie del lago.

Aquiles: No tanto. Es realmente muy similar a lo que hace el cerebro de uno cuando reconstruye el sonido reproducido en las cuerdas vocales de otra persona a partir de las vibraciones transmitidas por el tímpano del oído a las fibras en la cóclea.

Cangrejo: Ya veo. Pero aún no veo dónde entra la teoría de los números en el cuadro, o qué tiene que ver todo esto con mis discos.

Aquiles: Bueno, en las matemáticas de la recuperación-acústica, surgen muchas preguntas que tienen que ver con el número de soluciones de ciertas ecuaciones diofánticas. Ahora bien, el Sr. T ha estado tratando de hallar durante años una forma de reconstruir los sonidos de Bach tocando su clavicordio, lo cual sucedió hace más de doscientos años, a partir de cálculos que implican los movimientos de todas las moléculas en la atmósfera en el presente.

Oso Hormiguero: ¡Seguro que eso es imposible! ¡Ellas se han ido irrecuperablemente, se han ido para siempre!

Aquiles: Así piensan los ingenuos… Pero el Sr. T ha dedicado muchos años a este problema y llegó a comprender que toda la cuestión dependía del número de soluciones a la ecuación:

Tortuga: Yo podría explicar, por supuesto, cómo surge esta ecuación, pero estoy seguro de que ello los aburriría.

Aquiles: Resulta que la teoría de la recuperación-acústica predice que los sonidos de Bach pueden ser recuperados a partir del movimiento de todas las moléculas en la atmósfera, suponiendo que o BIEN existe por lo menos una solución a la ecuación…

Aquiles: Decía, “suponiendo que O BIEN existe tal solución o una demostración de que NO hay soluciones”. Y por eso el Sr. T se dedicó a trabajar cuidadosamente en ambos extremos del problema simultáneamente. Como resulta que el descubrimiento del contraejemplo era el ingrediente clave para encontrar la demostración, así un extremo guiaba directamente al otro.

Tortuga: Bueno, vea Ud., yo había demostrado que el desarrollo estructural de cualquier demostración del Teorema Final de Fermat —si existía uno— podía ser descrito por una elegante fórmula que, así sucedió, dependía de los valores de una solución a una cierta ecuación. Cuando encontré esta segunda ecuación, para mi propia sorpresa resultó ser la ecuación de Fermat. Una divertida relación accidental entre forma y contenido. Así, cuando encontré el contraejemplo, todo lo que necesité hacer fue usar aquellos números como una receta para construir mi demostración de que no había soluciones para la ecuación. Notablemente simple, si se lo piensa. No puedo imaginar por qué nunca nadie había hallado el resultado antes.

Aquiles: Como resultado de este suceso matemático inesperadamente enriquecedor, el Sr. T fue capaz de llevar a cabo la recuperación-acústica con la que tanto había soñado. Y el regalo del Sr. Cangrejo representa una realización palpable de todo este trabajo abstracto.

Cangrejo: ¡No me diga que es una grabación de Bach tocando sus propias obras para clavicordio!

Aquiles: Lo siento, pero debo hacerlo, ¡pues en realidad es precisamente eso! Ésta es una serie de dos discos de Johann Sebastian Bach tocando todo su Clavecín Bien Temperado. Cada disco contiene uno de los dos volúmenes del Clavecín Bien Temperado, es decir, cada disco contiene 24 preludios y fugas —una en cada tonalidad mayor y menor.

Cangrejo: Bueno, ¡entonces deberíamos poner uno de estos inapreciables discos inmediatamente! ¿Y cómo podré agradecerles alguna vez a Uds. dos?

Tortuga: Ya nos ha agradecido abundantemente con este delicioso té que ha preparado.

(El Cangrejo saca uno de los discos de su sobre y lo pone. El sonido de un clavicordista increíblemente magistral inunda la pieza con la más alta fidelidad imaginable. Uno incluso escucha —¿o es sólo nuestra imaginación?— el suave sonido de la voz de Bach cantando para sí mismo mientras toca…)

Cangrejo: ¿Le gustaría a alguno de Uds. seguir la partitura? Resulta que tengo una edición única del Clavecín Bien Temperado, especialmente ilustrada por un profesor mío que resultó ser también un calígrafo inusualmente fino.

(El Cangrejo se dirige a su elegante librero de vidrio y madera, abre las puertas y extrae dos grandes volúmenes.)

Cangrejo: Aquí tiene, Sr. Tortuga. Realmente nunca he llegado a conocer todas las bellas ilustraciones de esta edición. Quizá su regalo me proveerá del ímpetu necesario para hacerlo.

Oso Hormiguero: ¿Ha notado alguna vez cómo en estas piezas el preludio siempre dispone el ánimo para la fuga que sigue?

Cangrejo: Sí. Aunque puede ser difícil traducirlo en palabras, siempre hay alguna sutil relación entre ambos, aun si el preludio y la fuga no tienen un tema melódico común, no obstante siempre hay alguna cualidad abstracta intangible que subyace a ambos, ligándolos muy estrechamente.

Tortuga: Y hay algo muy dramático en esos pocos momentos de silencio suspendidos entre el preludio y la fuga —ese momento donde el tema de la fuga está por sonar en tonos sucesivos, que se unen luego a sí mismos en complejos niveles siempre crecientes de misteriosa y exquisita armonía.

Aquiles: Sé precisamente a qué se refiere. Hay tantos preludios y fugas que no he llegado a conocer aún y para mí ese momentáneo interludio de silencio es muy excitante; es un momento muy fugaz en que intento anticipar al Viejo Bach. Por ejemplo, siempre me pregunto cuál será el tiempo de la fuga: ¿allegro o adagio? ¿Será 6/8 o 4/4? ¿Tendrá tres voces o cinco —o cuatro? Y entonces, comienza la primera voz… Es un momento tan exquisito.

Cangrejo: Ah, sí, recuerdo bien esos lejanos días de mi juventud, esos días en que me estremecía con cada nuevo preludio y fuga, lleno de excitación por su novedad y belleza y las muchas sorpresas inesperadas que ocultan.

Cangrejo: Ha sido suplantado por la familiaridad, como siempre lo será. Pero en esa familiaridad también hay una especie de profundidad que tiene sus propias compensaciones. Por ejemplo, encuentro que siempre hay nuevas sorpresas que no había notado antes.

Cangrejo: Quizás —especialmente cuando está invertido y escondido entre varias otras voces, o cuando parece venir irrumpiendo de las profundidades, desde la nada. Pero hay también modulaciones asombrosas que es maravilloso escuchar una y otra vez, y preguntarse cómo el Viejo Bach las pudo concebir.

Aquiles: Me alegra oír que aún haya algo que buscar, después de haber tenido ya el primer torrente de apasionamiento con el Clavecín Bien Temperado —aunque también me entristece que esta etapa no pueda durar para siempre.

Cangrejo: Oh, no tiene por qué temer, ya que su apasionamiento no morirá del todo. Una de las cosas agradables acerca de esa especie de estremecimiento juvenil es que siempre puede ser resucitado, justo cuando Ud. pensaba que estaba finalmente muerto. Sólo necesita de la clase correcta de desencadenamiento.

Cangrejo: Así como escucharlo con los oídos, por así decirlo, de alguien para quien es una experiencia totalmente nueva —alguien como Ud., Aquiles. De alguna manera la excitación se transmite y puedo sentirme estremecido nuevamente.

Aquiles: Qué intrigante. El estremecimiento ha permanecido dormido en alguna parte dentro suyo, pero es incapaz de hallarlo por sí mismo en su subconciente.

Cangrejo: Exactamente. El potencial para revivir el estremecimiento está “codificado”, de alguna manera desconocida, en la estructura del cerebro, pero no tengo el poder para excitarlo a voluntad; tengo que esperar la circunstancia fortuita para desencadenarlo.

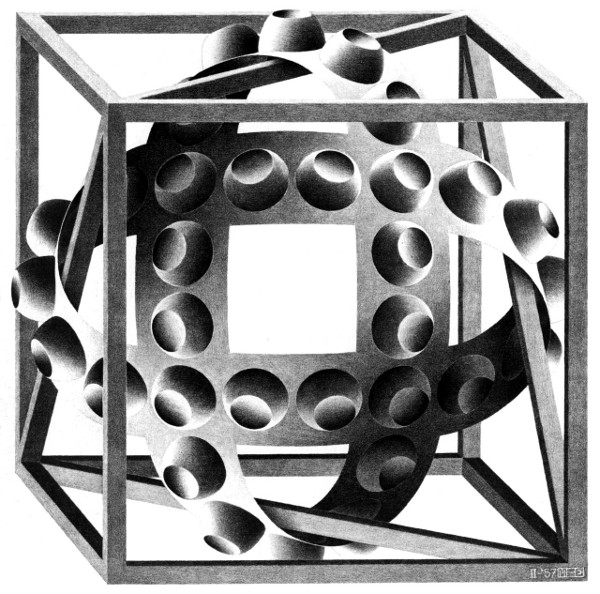
FIGURA 56. Cubo con Cintas Mágicas, de M. C. Escher (litografía, 1957).

Aquiles: Tengo una pregunta acerca de las fugas que me siento un poco avergonzado de hacer, pero, como sólo soy un novicio en lo de escuchar fugas, me estaba preguntando si acaso alguno de Uds., versados fugaescuchas, podría ayudarme a aprender…

Tortuga: Ciertamente a mí me gustaría ofrecerle mi propio y magro conocimiento, si probara ser de alguna utilidad.

Aquiles: Oh, gracias. Permítame llegar a la pregunta desde cierto ángulo. ¿Está Ud. familiarizado con el grabado llamado Cubo con Cintas Mágicas, de M. C. Escher?

Tortuga: ¿En el cual hay bandas circulares que tienen distorsiones tipo burbujas que, tan pronto como ha decidido Ud. que son montículos, parecen convertirse en hoyos —y viceversa?

Cangrejo: Recuerdo ese cuadro. Esas pequeñas burbujas siempre parecen saltar hacia atrás y hacia adelante viéndose cóncavas o convexas dependiendo de la dirección en que se las aproxima. No hay manera de verlas simultáneamente como cóncavas y convexas —de alguna manera nuestro cerebro no lo permite. Hay dos “modos” mutuamente excluyentes en que uno puede percibir las burbujas.

Aquiles: Justamente. Bueno, parece que he descubierto dos modos algo análogos en que puedo escuchar una fuga. Los modos son éstos: ya sea seguir una voz individual a la vez, o escuchar el efecto total de todas ellas juntas, sin tratar de destrenzar una de otra. He probado cada uno de estos modos y, para mi gran frustración, cada uno de ellos excluye al otro. Simplemente no está en mi poder seguir el curso de las voces individuales y al mismo tiempo escuchar el efecto total. Descubro que salto hacia atrás y hacia adelante entre un modo y otro, más o menos espontánea e involuntariamente.

Aquiles: Sí. Precisamente me estaba preguntando… ¿mi descripción de estos dos modos de escuchar fugas me marca inequívocamente como un auditor ingenuo y sin experiencia, quien no podría siquiera empezar a comprender los modos de percepción más profundos que existen más allá de su vista?

Tortuga: No, en absoluto, Aquiles. Sólo puedo hablar por mí, pero yo también me encuentro a mí mismo cambiando hacia atrás y hacia adelante de un modo al otro sin ejercer ningún control consciente sobre qué modo debería ser el dominante. No sé si nuestros demás compañeros aquí presentes han experimentado algo similar también.

Cangrejo: Definitivamente. Es un fenómeno absolutamente tormentoso, ya que uno siente que la esencia de la fuga está revoloteando sobre uno sin que uno la pueda agarrar del todo, ya que uno no puede funcionar de ambas maneras a la vez.

Oso Hormiguero: Las fugas tienen la interesante propiedad de que cada una de sus voces es una pieza de música en sí misma; y así una fuga puede ser pensada como una colección de varias piezas distintas de música, todas basadas en un tema único, y todas tocadas simultáneamente. Y depende del auditor (o su subconsciente) decidir si debe ser percibida como una unidad, o como una colección de partes independientes, todas las cuales armonizan.

Aquiles: Ud. dice que las partes son “independientes”, sin embargo eso puede no ser literalmente verdadero. Tiene que haber alguna coordinación entre ellas, de otra manera, cuando ellas fueran puestas juntas, uno sólo tendría un estrépito no sistemático de tonos, y eso está tan lejos de la verdad como podría estarlo.

Oso Hormiguero: Una mejor manera de plantearlo podría ser ésta: si escucha cada voz individual, descubrirá que ésta pareciera tener sentido en sí misma. Podría estar sola, y ése es el sentido en el que quise decir que era independiente. Pero tiene razón en señalar que cada una de estas líneas con sentido individual se funde con las otras de una manera altamente no aleatoria para crear una totalidad llena de gracia. El arte de escribir una fuga hermosa yace precisamente en esta habilidad: componer varias líneas diferentes, cada una de las cuales da la ilusión de haber sido escrita para realzar su propia belleza.

pero cuando son tomadas en conjunto forman un todo que de ninguna manera se siente forzado. Ahora bien, esta dicotomía entre escuchar una fuga como un todo y escuchar las voces que la componen, es un ejemplo particular de una dicotomía muy general que se aplica a muchas clases de estructuras formadas por niveles inferiores.

Aquiles: Oh, ¿realmente? ¿Se refiere a que mis dos “modos” pueden tener algún tipo más general de aplicabilidad, en situaciones distintas que el escuchar fugas?

Aquiles: Me pregunto cómo podría ser eso. Me imagino que tiene que ver con alternar entre percibir algo como un todo y percibirlo como una colección de partes. Pero el único lugar en que me he topado con esa dicotomía es al escuchar fugas.

Tortuga: Oh, no, ¡mire esto! Acabo de dar vuelta la página mientras seguía la música y me topé con esta magnífica ilustración frente a la primera página de la fuga.

Cangrejo: Nunca he visto esa ilustración antes. ¿Por qué no la hace circular?

(La Tortuga hace circular el libro. Cada miembro del cuarteto la mira de una forma característica, éste desde lejos, aquél desde cerca, cada uno ladeando su cabeza para acá y para allá con perplejidad. Finalmente ha dado la vuelta y regresa a la Tortuga, quien la observa muy atentamente.)

Aquiles: Bueno, me parece que el preludio está por terminar. Me pregunto si, al escuchar esta fuga, adquiriré mayor comprensión acerca de la pregunta “¿Cuál es la manera correcta de escuchar una fuga: como un todo, o como una suma de sus partes?”.

Preludio y…