FIGURA 134. Un “triángulo autoral”.
Bucles Extraños o Jerarquías Enredadas
DOS CAPÍTULOS ATRÁS, comenté el verdaderamente exitoso programa de damas creado por Arthur Samuel, único programa capaz de derrotar a su inventor. Es interesante, por ello, conocer las opiniones de Samuel sobre el tema de las computadoras y la originalidad. Los pasajes que siguen han sido tomados de una réplica, formulada por Samuel en 1960, dirigida a un artículo de Norbert Wiener.
Estoy convencido de que las máquinas no pueden poseer originalidad en el sentido afirmado por Wiener en su tesis de que “las máquinas pueden trascender, y lo hacen, ciertas limitaciones de sus diseñadores, y ello hace que lleguen a ser eficaces y al mismo tiempo peligrosas”. […]
Una máquina no es un genio, no funciona mediante toques mágicos, no posee una voluntad; pese a lo que diga Wiener, de aquélla no surge nada que no haya sido puesto previamente allí, salvo, por supuesto, en el caso nada frecuente de mal funcionamiento […]
Las “intenciones” que la máquina parece manifestar son las intenciones del programador humano, tal como fueron especificadas con anterioridad, o son intenciones subsidiarias, derivadas de aquéllas según reglas establecidas por el programador. Podemos prever niveles más elevados de abstracción, como lo hace Wiener, donde el programa no sólo modifique las intenciones subsidiarias sino también las reglas empleadas en su derivación, o donde modifique las formas a través de las cuales modifica las reglas, y así siguiendo, o, inclusive, donde una máquina inventaría y construiría una segunda máquina dotada de mayores capacidades. Sin embargo, y esto es importante, la máquina no hará y no podrá [el subrayado es de Samuel] hacer ninguna de tales cosas hasta que no haya sido instruida acerca de cómo proceder para ello. Hay, y lógicamente deberá seguirlo habiendo, una completa separación entre (i) toda extensión y elaboración sustancial en este proceso de concreción de los anhelos humanos, y (ii) el desarrollo, en el interior de la máquina, de una voluntad propia. Creer otra cosa es confiar en la magia, o suponer que la existencia de la voluntad humana es una ilusión, y que las acciones humanas son tan mecánicas como las de la máquina. Tal vez el artículo de Wiener y mi perorata respondan, ambos, a una determinación mecanicista, pero me niego a aceptarlo.[1]
Esto me trae a la memoria el Diálogo de Lewis Carroll (la Invención a dos voces); intentaré explicar por qué. Samuel basa su argumentación contra la conciencia (o la voluntad) de la máquina en la noción de que toda implantación mecánica de la voluntad requeriría una regresión infinita. De modo similar, la Tortuga de Carroll sostiene que no puede darse ningún paso de razonamiento, por simple que sea, sin aducir alguna regla de más alto nivel que le dé fundamento. Pero como eso último configura también un paso de razonamiento, es necesario recurrir a una regla de nivel aún más alto, y así siguiendo. Conclusión: el razonamiento involucra una regresión infinita.
Por supuesto, algo no está bien en el argumento de la Tortuga, y creo que ocurre algo análogo en el argumento de Samuel. Para mostrar que hay falacias análogas en ambos, voy a “ayudar al Diablo”, poniéndome transitoriamente en el papel de abogado del Diablo. (Puesto que, como es sabido, Dios ayuda a quienes se ayudan a sí mismos, es presumible que el diablo ayude a quienes, no se ayudan a sí mismos. ¿El Diablo se ayudará a sí mismo?). He aquí mis diabólicas conclusiones con respecto al diálogo carrolliano:
La deducción “el razonamiento es imposible” no se aplica a las personas porque, como cualquiera puede advertir, nosotros nos las arreglamos para dar muchos pasos de razonamiento, en los niveles superiores que fueren. Esto muestra que los seres humanos operamos sin necesidad de reglas: somos “sistemas informales”. Por otro lado, como argumento contrario a la posibilidad de toda implantación mecánica del razonamiento, la deducción es válida, pues todo sistema mecánico de razonamiento debería depender explícitamente de reglas; entonces, no podría salirse del juego a menos que haya metarreglas que establezcan cuándo aplicar sus reglas, metametarreglas que establezcan cuándo aplicar sus metarreglas, etc. Podemos concluir que la facultad de razonar no puede ser mecanizada: es un atributo exclusivamente humano.
¿Cuál es la falla del punto de vista del abogado del Diablo? Obviamente, el supuesto de que una máquina no puede hacer algo sin una regla que le indique hacerlo. En realidad, las máquinas escapan tan fácilmente como las personas a las disparatadas objeciones de la Tortuga y, además, por la misma razón: tanto las máquinas como los seres humanos están formados por un hardware que procesa todo por sí mismo, con arreglo a las leyes de la física. No hace falta basarse en “reglas que permitan aplicar las reglas”, porque las reglas de nivel inferior —las que no tienen enfrente ningún “meta”— están enclavadas en el hardware, y actúan sin necesidad de autorización. Moraleja: El Diálogo de Carroll no dice nada a propósito de las diferencias entre los seres humanos y las máquinas, al fin y al cabo. (Y, por cierto, el razonamiento es mecanizable).
Así que, pues, listo en el Diálogo de Carroll. Manos a la obra ahora con la argumentación de Samuel; su esencia, si se me permite caricaturizarla, es ésta:
Ninguna computadora “desea” nunca hacer nada, pues ha sido programada por alguien ajeno. Únicamente si pudiera programarse a sí misma desde cero —un absurdo— tendría un sentido volitivo propio.
Samuel reproduce la posición de la Tortuga, sustituyendo “razonar” por “desear”. Lo que implica su argumentación es que, detrás de toda mecanización del desear, deberá haber una regresión infinita o, pero aun, un bucle cerrado. Si es por esto que las computadoras carecen de voluntad, ¿qué ocurre con las personas? Un criterio idéntico supondría que:
Salvo que una persona se diseñe a sí misma y elija sus propias voliciones (como también que haga la elección de elegir sus propias voliciones, etc.) no se puede decir de ella que tiene albedrío propio.
Esto nos hace detenernos a pensar de dónde proviene nuestra noción de contar con albedrío propio. A menos que seamos espiritualistas, probablemente respondamos que de nuestro cerebro: una construcción hardware que no hemos elegido ni diseñado. Sin embargo, ello no debilita nuestro sentido de preferencia hacia ciertas cosas y de rechazo hacia otras. No somos un “objeto autoprogramado” (sea lo que fuere esto), pero así y todo tenemos un sentido de la volición, y éste emana del sustrato físico de nuestra organización mental. De la misma manera, algún día las máquinas podrán ejercitar voliciones, aun sin la intervención de un programa mágico, espontáneamente aparecido desde la nada en la memoria (un “programa autoprogramado”). Las máquinas serán capaces de actos de voluntad por las mismas razones que nosotros: como resultado de la organización y de la estructura de muchos niveles de hardware y de software. Moraleja: la argumentación de Samuel no dice nada a propósito de las diferencias entre los seres humanos y las máquinas, al fin y al cabo. (Y, por cierto, la voluntad será mecanizada).
Inmediatamente a continuación de la Invención de dos voces, expresé que un problema de importancia central en este libro es el siguiente: “¿Las palabras y los pensamientos están regidos, o no, por reglas formales?”. Una de las empresas principales acometidas en estas páginas ha sido la de hacer notar la proliferación de niveles que caracteriza a la mente/cerebro, y he procurado mostrar que la respuesta última a aquella pregunta es: “Si, a condición de que descendamos hasta el nivel más bajo —el hardware— para descubrir allí las reglas”.
Ahora bien, las afirmaciones de Samuel incluyen un concepto que me interesa analizar. Es el siguiente: cuando los seres humanos pensamos, indudablemente modificamos nuestras propias reglas mentales, y modificamos las reglas que modifican las reglas, y así siguiendo; pero de lo que aquí se habla es de, por decirlo así, “reglas software”. Por el contrario, las reglas ubicadas en el fondo no cambian. Las neuronas funcionan de la misma simple manera en todo momento. No se puede “pensar” a las neuronas para que funcionen de alguna forma no neuronal, mientras que sí es posible alterar el estilo de reflexión o el tema al que está abocada la mente. Lo mismo que Aquiles en el Preludio y Furmiga, se tiene acceso a los propios pensamientos pero no a las propias neuronas. Las reglas software, situadas en diversos niveles, pueden cambiar; no así las reglas hardware: ¡en realidad, la flexibilidad del software se debe a la rigidez del hardware! Esto no constituye, en absoluto, una paradoja, sino un hecho simple y fundamental, asociado a los mecanismos de la inteligencia.
Quiero dedicar este capítulo final a la distinción entre el automodificable software y el inviolable hardware, desarrollando el tema a través de un juego de variaciones. Algunas de éstas, tal vez, parezcan traídas de los cabellos; sin embargo, confío en que, cuando cierre el bucle mediante el retorno al cerebro, la mente y la noción de conciencia, el lector encuentre un núcleo invariante en todas las variaciones.
Mi interés mayor, en este capítulo, es transmitir algunas de las imágenes que más me ayudaron a visualizar la forma en que la conciencia brota de la jungla de neuronas; transmitir, en suma, un conjunto de intuiciones intangibles, en la esperanza de que sean válidas y puedan así contribuir, en alguna medida, a que otros lleguen a afinar la formulación de sus propias imágenes acerca de lo que hace funcionar a la mente. Todo lo que yo puedo esperar es que las confusas imágenes de mi propia mente, acerca de la mente y de las imágenes, catalicen la formación de imágenes más certeras, acerca de la mente y de las imágenes, en otras mentes.
Una primera variación se refiere a algunos juegos en los cuales, cuando es nuestro turno, podemos modificar las reglas. Consideremos el ajedrez: evidentemente, las reglas son siempre las mismas, lo único que cambia con cada movida es la situación del tablero. Ahora bien, inventemos una variación consistente en que, cuando nos toca jugar, hagamos una movida o, en lugar de ello, modifiquemos las reglas. ¿Cómo hacerlo, empero? ¿Con total libertad? ¿Lo convertimos en un juego de damas? Por cierto, semejante anarquía carecería de propósito; debemos establecer algunas restricciones: por ejemplo, una versión podría permitir que se redefina el movimiento del caballo. En vez de ser l-y-luego-2, podría ser m-y-luego-n, donde m y n sean números naturales arbitrarios; llegado nuestro turno, podríamos cambiar tanto a m como a n por más o menos 1, de modo que el movimiento podría ir desde 1-2 a 1-3 a 0-3 a 0-4 a 0-5 a 1-5 a 2-5… También sería posible contar con reglas que redefinan los movimientos del alfil, y de todas las piezas restantes. Además, se podrían agregar escaques, o reducir los existentes…
Tenemos ahora dos estratos de reglas: las que indican cómo mover las piezas, y las que indican cómo modificar las reglas. Tenemos entonces reglas y metarreglas. El paso que sigue es obvio: introducir metametarreglas gracias a las cuales podamos cambiar las metarreglas. Lo que no es tan obvio es cómo conseguir esto. La razón por la que es sencillo formular reglas relativas al movimiento de las piezas consiste en que éstas se desplazan en un espacio formalizado: el tablero. Si podemos idear una notación formal simple para expresar reglas y metarreglas, manipularlas será como manipular formalmente cadenas o, inclusive, como manipular piezas de ajedrez. Para llevar las cosas a su extremo lógico: incluso, sería posible expresar las reglas y las metarreglas como posiciones, en tableros auxiliares. Luego, una determinada posición del tablero podría ser interpretada como una partida, o como un conjunto de reglas, o como un conjunto de metarreglas, etc., según el criterio que nos interese aplicar en cada oportunidad. Por supuesto, deberá existir acuerdo entre los jugadores en cuanto a las convenciones que rijan la interpretación de la notación.
Podemos contar, pues, con un gran número de tableros adyacentes: uno para la partida, otro para las reglas, otro para las metarreglas, otro para las metametarreglas, y así siguiendo hasta donde se desee. El jugador a quien toca el turno puede hacer una movida en cualquiera de los tableros, excepto en el de máximo nivel, siguiendo las reglas que correspondan (se aplican las del tablero ubicado inmediatamente a continuación en la jerarquía). Indudablemente, los jugadores pueden llegar a sentirse por completo desorientados ante el hecho de que casi todo —¡pero no todo!— puede modificarse. Por definición, el tablero de nivel superior no puede ser alterado: es inviolable. Hay otras cosas inviolables: las convenciones en virtud de las cuales son interpretados los tableros, el acuerdo de jugar por turnos, el de que cada jugador puede modificar un tablero por turno… pueden encontrarse más si se examina detenidamente la idea.
Y es posible ir mucho más adelante, desplazando los pilares que permiten establecer la orientación. Un paso por vez… comenzamos por yuxtaponer toda la hilera de tableros en uno solo. ¿Cómo proceder luego? Habrá dos formas de interpretar el tablero: (1) como conjunto de piezas sujetas a movimiento; (2) como reglas que gobiernan el movimiento de las piezas. Ahora bien, cuando nos toca el turno, movemos piezas, ¡y, forzosamente, modificamos las reglas! De tal modo, las reglas se transforman a sí mismas constantemente: esto impresiona como un reflejo de la Tipogenética, y de la misma genética real. La distinción entre partida, reglas, metarreglas, metametarreglas, se ha perdido. Lo que una vez fue una esmerada disposición jerárquica se ha convertido en un Bucle Extraño O Jerarquía Enredada. Las movidas cambian las reglas, las reglas determinan las movidas… giro tras giro en tomo al mismo punto… Aún hay diferentes niveles, pero la distinción entre “más bajo” y “más alto” se ha borrado.
Ahora, parte de lo que ere inviolable se ha hecho modificable, pero resta una multitud de inviolabilidades. Igual que antes, hay convenciones entre ambos oponentes, destinadas a interpretar el tablero como un grupo de reglas; hay acuerdo en cuanto a la distribución de turnos, como asimismo, probablemente, otras convenciones implícitas.
Adviértase, con todo, que la noción de existencia de diferentes niveles ha sobrevivido, de una manera inesperada. Hay un nivel Inviolable, llamémosle nivel I, en el cual reside la interpretación de las convenciones; y hay también un nivel Enredado, el nivel E, donde reside la Jerarquía Enredada. De modo que hay dos niveles que siguen siendo jerárquicos: el nivel I gobierna lo que sucede en el nivel E, pero el nivel E no afecta, y no puede afectar, al nivel I. Por más que el nivel E sea por sí mismo una Jerarquía Enredada, permanece bajo el control de un conjunto de convenciones ubicado fuera de él: y ésta es la cuestión importante.
Sin duda el lector ya lo imaginó: nada nos impide hacer lo “imposible”, es decir, entrelazar el nivel I y el nivel E, haciendo que la interpretación de las convenciones mismas quede sujeta a revisión, según la posición del tablero. Sin embargo, para concretar tal “superenredamiento”, ambos oponentes han de ponerse de acuerdo sobre ciertas convenciones nuevas que conecten los dos niveles… y el acto a través del cual se efectúe el acuerdo creará un nuevo nivel, un nuevo género de nivel inviolable por sobre (o por debajo, si así se prefiere) el nivel “superenredado”. Y es posible seguir por este camino hasta donde se quiera. En realidad, los “brincos” que se han practicado son muy similares a los vistos en la Cantatatata de cumpleaños, y en la reiterada gödelización aplicada a diversos perfeccionamientos de TNT. Cada vez que creemos haber alcanzado el punto terminal, hay una nueva variación del tema del brinco fuera del sistema, cuya delimitación requiere creatividad.
Pero no estoy interesado en proseguir con el curioso tema de los enredamientos cada vez más abstrusos que emanan del ajedrez automodificante. La intención fue mostrar, de una manera en cierta medida gráfica, que en todo sistema hay siempre algún nivel “protegido”, fuera del alcance de las reglas de otros niveles, por muy enredada que sea la interacción existente entre éstos. Un divertido acertijo del Capítulo IV ilustra la misma idea dentro de un contexto algo diferente. Tal vez pesque desprevenido al lector:
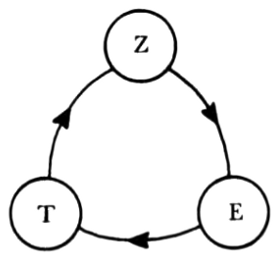
Hay tres autores: Z, T y E. Pero sucede que Z sólo existe en una novela de T. Del mismo modo, T sólo existe en una novela de E. Y, curiosamente, también E existe solamente en una novela… de Z, por supuesto. Ahora bien, ¿es realmente posible un “triángulo autoral” semejante?
Por supuesto que es posible. Pero hay una triquiñuela… Los tres autores Z, T y E son personajes de otra novela… ¡escrita por H! Uno puede considerar al triángulo Z-T-E un Bucle Extraño O Jerarquía Enredada, pero el autor H está fuera del espacio donde tiene lugar el entremezclamiento: el autor H es un espacio inviolable. Pese a que Z, T y E tienen acceso entre sí —directo o indirecto— y a que puedan ser muy cretinos unos con otros en sus respectivas novelas, ¡ninguno de ellos puede hacer contacto con la vida de H! Ni siquiera pueden imaginarlo, tal como no podríamos imaginar nosotros al autor del libro del cual fuésemos personajes. Si yo tuviera que representar gráficamente al autor H, lo dibujaría fuera de la página; claro, esto presentaría una dificultad, puesto que dibujar algo es, necesariamente, ubicarlo en la página… De todos modos, H está fuera, en rigor, del mundo de Z, T y E, y tiene que ser representado en función de ello.

FIGURA 134. Un “triángulo autoral”.
Una variación clásica de nuestro tema es la obra de Escher, Manos dibujando (figura 135). En ella, una mano izquierda (MI) dibuja una mano derecha (MD), y al mismo tiempo MD dibuja a MI. Otra vez nos encontramos con niveles comúnmente considerados jerárquicos —el que dibuja, y el que es dibujado— que se vuelven uno hacia el otro, originando una Jerarquía Enredada. Pero el tema de este capítulo se funda, por supuesto, en lo que hay más allá, en la mano no dibujada pero dibujante de M. C. Escher, creador de MI y de MD. Escher está fuera del espacio configurado por las dos manos y, en mi esquemática versión de su cuadro (figura 136), esto puede ser observado explícitamente. En dicho esquema representativo de la imagen de Escher se ve, arriba, el Bucle Extraño O Jerarquía Enredada; abajo, está el Nivel Inviolable, el cual hace posible que exista el nivel superior. Se podría, inclusive, avanzar más todavía y escherizar el cuadro de Escher mediante una fotografía que mostrase una mano dibujándolo. Y así siguiendo.
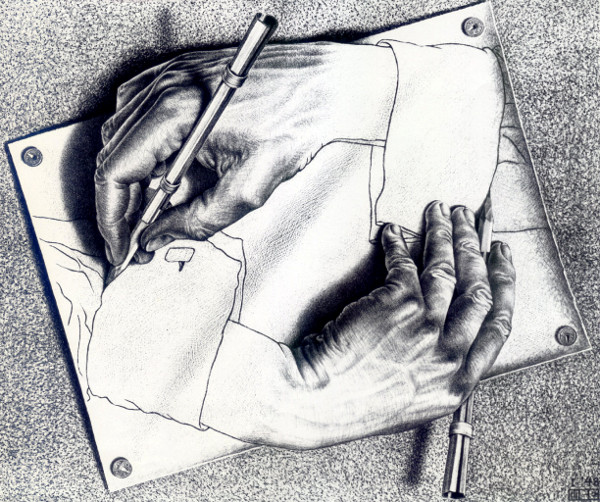
FIGURA 135.
Manos dibujando, de M. C. Escher (litografía, 1948).
FIGURA 136. Diagrama abstracto de Manos dibujando, de Escher. Arriba, una aparente paradoja. Abajo, su resolución.
Podemos ahora poner en relación lo anterior tanto con el cerebro como con los programas IA. En nuestros mecanismos de pensamiento, los símbolos activan otros símbolos, y todos interactúan heterárquicamente. Además, los símbolos puede modificarse internamente entre sí, a la manera de los programas que actúan sobre otros programas. Como consecuencia de la Jerarquía Enredada que envuelve los símbolos, se crea la ilusión de que no hay nivel inviolable; se piensa que tal nivel no existe porque está fuera de nuestra visión.
Una esquematización de esta imagen en su conjunto podría estar dada por una gigantesca selva de símbolos enlazados entre sí por enmarañadas líneas, semejantes a las enredadas de una jungla tropical: éste sería el nivel superior, la Jerarquía Enredada donde el pensamiento mismo fluye por todas partes; es el elusivo nivel de la mente, lo análogo a MI y MD. Por debajo, en esta representación, y en analogía con Escher como invisible “causante primero”, estarían figuradas las miríadas de neuronas —el “sustrato inviolable”— que hacen posible la existencia del entremezclamiento superior. Es interesante la circunstancia de que este nivel inferior es, a su vez, un entremezclamiento, en términos literales: miles de millones de células y centenares de miles de millones de axones, reunidos en un todo.
Se trata de un caso llamativo, el presente, donde un enmarañamiento software, el de los símbolos, se sustenta en un enmarañamiento hardware, el de las neuronas. Pero únicamente el enmarañamiento simbólico es una Jerarquía Enredada; el neural es sólo un enmarañamiento “simple”. La distinción es casi la misma que la establecida en el Capítulo XVI, entre Bucles Extraños y retroalimentación. Una Jerarquía Enredada aparece cuando lo que se suponía una serie de niveles nítidamente jerárquicos nos da la sorpresa de cerrarse sobre sí misma, de una manera que viola el principio jerárquico. El elemento de sorpresa es importante, y es por ello que llamo “extraños” a estos Bucles Extraños. Un enredamiento simple, como el que presenta la retroalimentación, no implica la transgresión de la distinción de niveles que se ha dado por supuesta; un ejemplo nos lo brinda la situación común de lavarse el brazo izquierdo con el derecho, y viceversa, cuando se está en la ducha; no hay ninguna extrañeza en esta imagen. ¡Por algo es que Escher optó por dibujar manos que dibujan manos!
Hechos tales como un par de brazos que se lavan entre sí ocurren en el mundo a cada momento, y no vemos en ellos nada de particular. Yo le digo algo a un interlocutor, y éste me responde algo a mí; ¿es paradójico esto? No: las percepciones de uno con respecto al otro no involucran una jerarquía preexistente, de modo que de aquí no surge ningún sentido de extrañeza.
Por otro lado, el lenguaje origina bucles extraños cuando habla de sí mismo, sea directa o indirectamente. En este caso, algo interior al sistema brinca hacia afuera y actúa sobre el mismo, como si fuera exterior a éste. Lo que nos perturba aquí quizá sea un sentido mal definido de la inexactitud topológica: la distinción interior-exterior es borrada, como en la célebre configuración llamada “botella de Klein”; aun cuando el sistema sea una abstracción, nuestra mente apela a la imaginación espacial, con la ayuda de una suerte de topología mental.
Volviendo al enredamiento simbólico: si concentramos nuestra atención en él, y olvidamos el enredamiento neural, creeremos estar en presencia de un objeto autoprogramado, exactamente igual que, si olvidamos la existencia de Escher, podemos dejarnos ganar por la ilusión de estar viendo, en Manos dibujando, un cuadro que se pinta a sí mismo. Es bastante inverosímil que esto ocurra con respecto a esa pintura, pero no lo es con respecto a los seres humanos, y al modo en que éstos analizan su mente. Los seres humanos nos sentimos autoprogramados. Está claro que no nos podemos sentir de otra manera, puesto que estamos aislados en relación con los niveles más bajos, esto es, en relación con el enredamiento neural. Nuestros pensamientos, aparentemente, circulan en el interior de su espacio propio, creando nuevos pensamientos y modificando los anteriores, y jamás nos percatamos de la contribución que nos están brindando nuestras neuronas… Pero es lo que era de esperar; no podemos hacer otra cosa.
Un double-entendre análogo puede ser observado en los programas Lisp que han sido ideados para acceder a su propia estructura y modificarla. Si se los examina en el nivel Lisp, uno diría que se modifican a sí mismos; pero si se eligen otros niveles para ubicar la perspectiva, y se considera a los programas Lisp como datos para el intérprete Lisp (véase Capítulo X), se verá que en realidad el único programa que está siendo procesado es el intérprete, y los cambios producidos no serán otra cosa que cambios en los grupos de datos. El intérprete Lisp, por su parte, no es pasible de modificaciones.
El modo en que uno describa una situación enmarañada de este género depende de cuántos pasos retrospectivos se den antes de proceder a dicha descripción. Si se vuelve atrás lo suficiente, en la mayor parte de los casos quedarán a la vista las pistas que conduzcan a cosas desenmarañadas.
Una área fascinante de enredamiento de jerarquías es el gobierno, particularmente las cortes de justicia. Por regla general, uno piensa que dos litigantes presentan su respectivo alegato ante la corte, y que ésta produce un fallo; la corte está ubicada en un nivel diferente al de los litigantes. Sin embargo, pueden suceder cosas extrañas cuando las cortes mismas se enmarañan en casos legales. De ordinario, hay un tribunal de nivel superior, ajeno al litigio. Inclusive cuando dos tribunales de inferior nivel se ven envueltos en alguna extraña pendencia, y cada uno de ellos reclama jurisdicción por encima del otro, hay algún tribunal de nivel superior que permanece exterior al enfrentamiento: en cierto sentido, esto es análogo a la interpretación inviolable de las convenciones, que comentamos líneas atrás, relativas al estrafalario ajedrez que imaginamos.
¿Pero qué ocurre cuando no hay tribunal superior, y la propia Corte Suprema se ve enmarañada en dificultades legales? Ésta fue prácticamente la clase de embrollo que se produjo en Estados Unidos con el caso Watergate. El entonces Presidente amenazó con obedecer exclusivamente un “dictamen definitivo” de la Corte Suprema… y luego sostuvo que él tenía derecho a decidir qué es “definitivo”. La amenaza nunca fue cumplida; si lo hubiese sido, habría tenido lugar una monumental confrontación entre dos niveles de gobierno, cada uno de los cuales, en cierta medida, puede afirmar válidamente que está por “encima” del otro… ¿y a quién se debe recurrir para que determine cuál está en lo cierto? Responder “el Congreso” no resuelve el problema, pues si éste ordena al Presidente que obedezca a la Corte Suprema, el Presidente podría negarse, aduciendo que cuenta con el derecho legal de desobedecer a la Corte Suprema (¡y al Congreso!) bajo ciertas circunstancias. Esto crearía un nuevo litigio, ¡y desordenaría el sistema entero, por tratarse de algo tan imprevisto… tan Enredado… tan Extraño!
La ironía está en que una vez que uno se ha golpeado la cabeza contra el techo de esta manera, quedando consecuentemente impedido de brincar fuera del sistema, en búsqueda de una autoridad aún más alta, a lo único que se puede apelar es a las fuerzas que impresionan como las más deficientemente definidas por reglas, pero que son la fuente exclusiva, a todas luces, de las reglas de más alto nivel: las reglas de nivel inferior, que en este caso equivalen a la reacción general de la sociedad. Bueno es recordar que, en sociedades como las nuestras, el sistema legal es, en cierto sentido, un gesto de urbanidad convenido colectivamente por millones de personas, y que puede ser dejado a un lado con la misma facilidad con que un río puede salirse de cauce. Se produciría entonces una aparente anarquía; sin embargo, la anarquía tiene su propio género de reglas, en forma similar a la sociedad civilizada, salvo que operan desde el fondo, no desde la cima. Un estudioso de la anarquía podría tratar de descubrir las reglas que gobiernan el desenvolvimiento de las situaciones anárquicas en el tiempo, y es muy probable que las encuentre.
En este punto, es útil la mención de una analogía que nos provee la física. Como ya se dijo con anterioridad, el equilibrio de los gases obedece a leyes simples que vinculan entre sí su temperatura, presión y volumen. No obstante, un gas puede violar estas leyes (tal como un Presidente puede violar otras), excepto dentro de un estado de equilibrio. En situaciones de no equilibrio, un físico que quiera describir lo que sucede puede recurrir tan sólo a la mecánica estadística, es decir, a un nivel de descripción que no es macroscópico, pues la explicación última del comportamiento de un gas se asienta siempre en el nivel molecular, así como la explicación última del comportamiento político de una sociedad se asienta siempre en las masas. El campo de la termodinámica del no equilibrio se impone el hallazgo de leyes macroscópicas que describan el comportamiento de gases (y de otros sistemas) despojados de equilibrio: su término análogo es la rama de la ciencia política que busca cuáles son las leyes que gobiernan las sociedades anárquicas.
Otras raras marañas producidas en el seno del gobierno incluyen, por ejemplo, las investigaciones de la policía acerca de sus propias iniquidades, un policía que es enviado a la cárcel mientras sigue en funciones, la autoaplicación de las reglas parlamentarias de procedimiento, etc. Uno de los casos legales más curiosos de que tengo noticia involucró a una persona que afirmaba tener poderes psíquicos. En realidad, sostenía que era capaz de utilizar esos poderes para detectar rasgos personales y ayudar así a los abogados a seleccionar jurados. ¿Y qué ocurriría si este “vidente” fuera sometido a juicio alguna vez? ¿Qué efecto provocaría ello sobre un miembro del jurado que creyera fervientemente en la percepción extra-sensorial? ¿En qué medida se sentiría afectado por el vidente (fuese éste un vidente auténtico o no)? El campo está listo par ser trabajado: una gran área para profecías autocumplidas.
Ya que hablamos de videntes y de percepción extrasensorial, podemos citar otra esfera de la vida donde abundan los bucles extraños: la pseudociencia; ésta se dedica a cuestionar gran parte de los procedimientos habituales y las creencias de la ciencia ortodoxa y a poner en discusión, por lo tanto, la objetividad científica. Propone entonces nuevas formas de interpretación de la evidencia, opuestas a las establecidas. Ahora bien, ¿cómo se evalúa una forma de interpretar la evidencia? ¿No se trata, otra vez, del problema de la objetividad, llevado ahora a un plano más elevado? Estamos de nuevo ante la paradoja carrolliana de la regresión infinita, bajo una máscara distinta. La Tortuga postularía que, si se quiere mostrar que A es un hecho, se requiere evidencia al respecto: B. Pero, ¿cómo estar seguros de que B es la evidencia de A? Para mostrar esto, se requiere una metaevidencia: C. Y, con respecto a la validez de la metaevidencia, se requiere una metametaevidencia, y así en más, ad nauseam.
A pesar de este razonamiento, la gente tiene un sentido intuitivo de la evidencia, y ello se debe —para repetir un antiguo refrán— a que tiene incorporado a su cerebro un hardware que incluye algunas formas rudimentarias de interpretar la evidencia. Podemos atenernos a éstas, y sumar nuevas formas de la misma interpretación; así sucede que, inclusive, aprendemos cómo y cuándo dejar a un lado nuestros principales mecanismos básicos de interpretación de evidencia: por ejemplo, cuando tratamos de resolver trucos mágicos.
Muchos fenómenos de pseudociencia presentan muestras concretas de dilemas acerca de la evidencia. Por ejemplo, en muchas ocasiones, fuera de laboratorio, parecen producirse manifestaciones de percepción extrasensorial que, en laboratorio, se desvanecen misteriosamente. La explicación científica habitual de esto es que la percepción extrasensorial es un fenómeno irreal que no puede hacer frente a un escrutinio riguroso. Algunos creyentes (no todos, por cierto) de la percepción extrasensorial tienen una manera peculiar de presentar batalla. Dicen: “No, la percepción extrasensorial es real; sencillamente, ocurre que se hurta cuando se trata de observarla científicamente: es contraria a la naturaleza de la visión científica del mundo”. Tenemos aquí una técnica sorprendentemente desenfadada, a la que podríamos denominar la técnica de “sacarse el problema de encima”. Es decir, en vez de cuestionar el asunto que se tiene entre manos, se arrojan dudas sobre las teorías pertenecientes a un nivel superior de credibilidad. Quienes aceptan la percepción extrasensorial insinúan que lo erróneo no está en sus ideas, sino en el sistema de creencias de la ciencia, lo cual implica un reclamo un tanto rimbombante: a menos que resulte apoyado por una evidencia abrumadora, sería conveniente mantenerse escéptico a su respecto. Sin embargo, otra vez estamos hablando de “evidencia abrumadora”, ¡como si todo el mundo estuviese de acuerdo acerca de lo que significa semejante cosa!
El entrelazamiento Sagredo-Simplicio-Salviati, mencionado en los Capítulos XIII y XV, aporta otro ejemplo a propósito de las complejidades que presenta la evaluación de evidencia. Sagredo trata de hallar alguna avenencia, en lo posible, entre los opuestos puntos de vista de Simplicio y Salviati. Pero no siempre es factible una transacción. ¿Cómo se puede forjar, “imparcialmente”, una avenencia entre lo correcto y lo erróneo? ¿Entre lo parcial y lo imparcial? ¿Entre avenencia y desavenencia? Estos interrogantes reaparecen en numerosas oportunidades, bajo la forma de apreciaciones relativas a cosas corrientes.
¿Es posible definir qué es la evidencia? ¿Es posible formular leyes que indiquen cómo asignar un sentido a las situaciones? Es probable que no, pues toda regulación rígida tendría, indudablemente, excepciones, y no reglas. Contar con un programa IA inteligente tampoco resolvería el problema pues, en tanto que procesador de evidencia, no sería en absoluto menos falible que los seres humanos. Entonces, si después de todo la evidencia es algo tan intangible, ¿por qué estoy tan prevenido contra formas nuevas de interpretación de la misma? ¿Es que soy incoherente? No creo esto. Lo que pienso es que se pueden establecer pautas orientadoras, y luego elaborar síntesis orgánicas a partir de ellas. No obstante, será inevitable que ingrese a la escena cierta dosis de discernimiento y de intuición… cosas que son diferentes en cada persona. Y que también serán diferentes en cada programa IA. En última instancia, hay complicados criterios para decidir si un método de evaluación de evidencia es eficaz. Uno de ellos se refiere a la “utilidad” de las ideas que llevaron al tipo de razonamiento en cuestión: las modalidades de pensamiento que, en la vida, han conducido a la obtención de cosas útiles son consideradas, en algún sentido, “válidas”. Con todo, este concepto de “útil” es sumamente subjetivo.
Creo que el proceso por el cual decidimos qué es válido o qué es verdadero constituye un arte, y que descansa a tal profundidad en un sentido de la belleza y de simplicidad que su asiento son los principios fundamentales básicos de la lógica, o del razonamiento o de cualquier otra cosa que pueda ser objetivamente formalizada. No estoy diciendo que (1) la verdad es una quimera, ni que (2) la inteligencia humana es, en principio, no programable. Sí estoy diciendo que (1) la verdad es demasiado elusiva como para que un ser humano o cualquier grupo de seres humanos la abarque nunca en su plenitud; y (2) la Inteligencia Artificial, cuando alcance el nivel de la inteligencia humana —y también si lo sobrepasa— se verá saturada de problemas relativos al arte, la belleza y la simplicidad, y se estrellará constantemente contra estas cosas mientras ejercita su propia búsqueda de conocimiento y comprensión.
“¿Qué es la evidencia?”. No es solamente un interrogante filosófico, pues lo encontramos en todos los ámbitos de la vida. Uno se enfrenta, a cada momento, con un extraordinario número de distintas elecciones posibles en cuanto a cómo interpretar la evidencia. Es casi imposible no ver en cualquier librería (y, en la actualidad, ¡en cualquier supermercado, inclusive!) obras sobre clarividencia, percepción extrasensorial, ovnis, el Triángulo de las Bermudas, astrología, rabdomancia, psicoalfacontrol, agujeros negros, creación contra evolución, biorretroalimentación, meditación trascendental, nuevas teorías psicológicas… En el campo de la ciencia, presenciamos enconados debates acerca de la teoría de la catástrofe, de la referente a las partículas elementales, de los agujeros negros, del problema de la verdad y la existencia en matemática, del libre albedrío, de la Inteligencia Artificial, de la oposición reduccionismoholismo… En un sector más pragmático de la vida, hay polémicas en torno a la eficacia de la vitamina C, al volumen de las reservas petrolíferas (naturales y almacenadas), a las causas de la inflación y del desempleo, etc., etc. Hay antipsiquiatría, budismo zen, paradojas de Zenón, psicoanálisis, y tantos y tantos temas más… Desde los más triviales, como por ejemplo la manera en que las tiendas deben disponer los libros que venden, hasta los más vitales, como por ejemplo el de cuáles son las ideas que han de ser enseñadas a los niños en las escuelas, en todos los temas, los medios para interpretar la evidencia juegan un papel sustancial.
Uno de los problemas más difíciles en materia de interpretación de evidencia es el que se plantea cuando se intenta determinar quiénes somos, a partir de la interpretación de la totalidad de las confusas señales exteriores. Las posibilidades, en este caso, de conflictos entre niveles, e interiores a cada nivel, son enormes. Los mecanismos psíquicos tienen que habérselas, simultáneamente, con la necesidad interna de autoestimación y con el constante flujo de evidencia, proveniente del exterior, que afecta tal imagen. El resultado es que la información fluye, a través de un complejo remolino, entre los diversos niveles de la personalidad; conforme gira el torbellino, algunas de sus partes se ven magnificadas, reducidas, negadas o, como sea, distorsionadas; luego, se van amoldando de nuevo a la misma especie de remolino, y así una y otra vez… todo ello en procura de reconciliar lo que es con lo que desearíamos que fuera (véase figura 81).
Finalmente, la imagen total de “quién soy” es incorporada, de alguna manera enormemente compleja, dentro del conjunto de la estructura mental, y contiene una gran cantidad de incoherencias irresueltas o, probablemente, irresolubles. De aquí proviene, con toda seguridad, gran parte de la tensión dinámica que integra de modo tan significativo al ser humano. La tensión entre las nociones interiores y las exteriores sobre quiénes somos da origen a las diversas orientaciones hacia determinados objetivos, y ello es lo que hace algo único de cada uno de los seres humanos. Así, paradójicamente, un elemento que todos tenemos en común —el hecho de ser criaturas autorreflexivas— conduce a una rica diversidad en cuanto a las maneras en que internalizamos la evidencia relativa a todo género de cosas, y acaba por ser una de las fuerzas más vigorosas en la plasmación de individualidades diferenciadas.
Es natural que surja la pretensión de trazar paralelos entre las personas y aquellos sistemas formales lo suficientemente elaborados como para que, igual que los seres humanos, cuenten con “autoimágenes” de la especie comentada. El Teorema de Gödel muestra que los sistemas formales coherentes, dotados de autoimagen, padecen de limitaciones fundamentales. ¿Tiene una extensión más amplia esta situación? ¿Existe un “Teorema de Gödel de la psicología”, por ejemplo?
Si se emplea el Teorema de Gödel como una metáfora, como una fuente de inspiración, en lugar de empeñarse en su traducción literal al lenguaje de la psicología o de cualquier otra disciplina, quizá se conseguiría la aparición de nuevas propuestas en estos campos del saber. Ahora bien, carece de todo fundamento practicar la traducción directa del Teorema a enunciados de otra disciplina, y considerar que éstos son válidos. Es un error enorme pensar que los resultados obtenidos, gracias a una notable dedicación, en la esfera de la lógica matemática, pueden ser manejados sin modificación en el interior de esferas completamente diferentes.
Pienso que puede ser sumamente interesante la traducción del Teorema de Gödel a otros ámbitos, a condición de dejar especificado en forma previa que la traducción es metafórica, y que no se proyecta una equivalencia literal. Dicho esto, agrego que, a mi entender, hay dos vías sobresalientes de utilización de analogías que conecten al Teorema de Gödel con los pensamientos humanos; una nos orienta hacia la cuestión de interrogarnos acerca de nuestra propia cordura: ¿cómo determino que estoy cuerdo? Se trata, por cierto, de un Bucle Extraño. Si uno comienza a indagarse a propósito de la propia cordura, puede quedar atrapado en una vorágine cada vez más intensa de profecías autocumplidas, aunque este proceso no sea, en absoluto, inevitable. Todos sabemos que el insano interpreta al mundo con arreglo a su lógica, la cual es coherente de un modo peculiar; ¿y cómo establecemos si nuestra propia lógica es “peculiar” o no, puesto que no tenemos más que esa misma lógica propia para juzgarnos? No tengo respuesta frente a esto, y me limito entonces a recordar el segundo Teorema de Gödel, según el cual las únicas versiones de teoría formal de los números que afirman su propia coherencia son incoherentes…
Otro desprendimiento metafórico del Teorema de Gödel dotado, según creo, de provocatividad intelectual, sugiere que, en último término, no podemos comprender nuestras propias mentes/cerebros. Esta idea tiene tanta amplitud y tantos niveles posibles que se debe ser muy cauto al proponerla. ¿Qué significa “comprender nuestras propias mentes/cerebros”? Podría tratarse de contar con una noción general acerca de cómo funcionan, tal como la noción que tiene un mecánico acerca del funcionamiento de un automóvil. Podría tratarse de una explicación completa de por qué los seres humanos hacen todas y cada una de las cosas que hacen. Podría tratarse de tener una comprensión completa de la estructura física del propio cerebro, en todos los niveles. Podría tratarse de disponer de un diagrama completo de la distribución cerebral, mostrada en un libro (ya en una biblioteca, ya en una computadora). Podría querer decir que se conoce con precisión, en todo momento, qué está sucediendo en el nivel neural de nuestro cerebro: cada excitación, cada alteración sináptica, etc. Podría querer decir que se ha formulado un programa que aprueba la verificación Turing. Podría querer decir que nuestro autoconocimiento es tan perfecto que nociones tales como la de subconciencia e intuición carecen de sentido, porque todo ha quedado a la vista. Podría significar una multitud de otras cosas.
¿Cuál de estos autorreflejos, si es que hay alguno que lo consigue, tiene mayor semejanza con el autorreflejo del Teorema de Gödel? Yo tengo dudas al respecto; algunos son sumamente disparatados, como por ejemplo la posibilidad de registrar el propio estado cerebral en todos sus detalles: esto es una ilusión que merece una papirotada, es una propuesta absurda y falta de interés para ser tenida en cuenta ahora; y, si el Teorema de Gödel sugiere que es algo imposible, mal podemos tomarla como una revelación. En cambio, la ancestral preocupación de conocerse a sí mismo de una manera profunda —llamémosle “comprender la propia estructura psíquica”— tiene un aura de verosimilitud. Sin embargo, ¿no habrá algún bucle vagamente gödeliano que limite la profundidad hasta la cual puede penetrar en su propia psique un individuo? No podemos vernos la cara con nuestros propios ojos, ¿no será razonable entonces que, del mismo modo, no podamos reflejar nuestras estructuras mentales completas en los símbolos que éstas elaboran?
Todos los teoremas limitativos de la metamatemática y de la teoría de la computación insinúan que, una vez alcanzado determinado punto crítico en la capacidad de representar nuestra propia estructura, llega el momento del beso de la muerte: se cierra toda posibilidad de que podamos representarnos alguna vez a nosotros mismos en forma integral. El Teorema de la Incompletitud, de Gödel; el Teorema de la Indecidibilidad, de Church; el Teorema de la Detención, de Turing; el Teorema de la Verdad, de Tarski: todos ellos tienen las resonancias de ciertos antiguos cuentos de hadas, advirtiéndonos que “perseguir el autoconocimiento es iniciar un viaje que… nunca estará terminado, no puede ser trazado en un mapa, nunca se detendrá, no puede ser descrito”.
Ahora bien, ¿los seres humanos aceptan los Teoremas limitativos? Tenemos aquí una vía de refutación. O soy coherente o soy incoherente. (Esto último es lo más probable, pero en beneficio de la completitud voy a tomar en cuenta ambas posibilidades). Si soy coherente, tendremos dos variantes, (1) la de “baja fidelidad”: mi autocomprensión está por debajo de un determinado punto crítico; en tal caso, soy incompleto, por hipótesis; (2) la de “alta fidelidad”: mi autocomprensión ha alcanzado el punto crítico donde le cabe la aplicación metafórica de los Teoremas limitativos, de modo que mi autocomprensión socava sus propios cimientos de una manera gödeliana, y resulto incompleto, por tal razón. Las variantes (1) y (2) son aseveraciones relativas a mi ser ciento por ciento coherente, supuesto realmente muy improbable; lo más creíble es que yo sea incoherente, lo cual es peor, pues significa que en mi interior hay contradicciones, ¿y entonces cómo puedo comprender alguna vez tal cosa?
Coherente o incoherente, nadie escapa al misterio del yo. Probablemente, todos seamos incoherentes; el mundo es demasiado complicado como para que una persona pueda darse el lujo de conciliar entre sí todas sus creencias individuales. Además, tensión y confusión son importantes en un mundo donde deben adoptarse muchas decisiones rápidas. Dijo una vez Miguel de Unamuno: “Si una persona no se contradice nunca, ha de ser porque no dice nada”. Yo diría que todos estamos en el mismo barco de aquel maestro Zen que, después de contradecirse varias veces consecutivas, dijo al confundido Doko: “Yo no puedo comprenderme a mí mismo”.
Quizá la mayor contradicción que afrontamos en nuestra existencia, la más ardua de asimilar, consista en saber que “hubo un tiempo en que yo no estaba vivo, y llegará un tiempo en que yo no esté vivo”. En un nivel, cuando “brincamos fuera de nosotros mismos” y nos vemos simplemente “como otro ser humano”, ello adquiere pleno sentido. Sin embargo, en otro nivel, tal vez más profundo, la no existencia personal carece de todo sentido. Todo lo que sabemos está integrado a nuestra mente, y por ende todo lo que no esté en el universo carece de comprensibilidad. Se trata de un innegable problema básico de la vida; y, posiblemente, el de mayor proximidad metafórica con respecto al Teorema de Gödel. Cuando tratamos de imaginar nuestra no existencia, hacemos la prueba de brincar fuera de nosotros mismos, proyectándonos en algún otro. Nos ilusionamos creyendo que podemos implantar en nuestro interior una perspectiva externa acerca de nosotros mismos, tal como TNT “cree” que refleja su propia metateoría únicamente en una cierta medida, no en forma completa; en cuanto a nosotros, aunque imaginemos que hemos podido brincar fuera de nosotros mismos, en realidad jamás podemos hacerlo… nos pasa como al dragón de Escher, con su pretensión de brincar fuera de su originario plano bidimensional para alcanzar la tridimensionalidad. Como quiera que sea, esta contradicción es tan grande que, durante la mayor parte de nuestra existencia, hacemos como si no la viéramos, pues afrontarla no nos conduce a ninguna parte.
Las mentes zen, por su parte, se complacen en esta inconciliabilidad. Una y otra vez, arrostran el conflicto entre la creencia oriental: “El mundo y yo somos uno, de modo que la noción de interrupción de mi existencia es una contradicción en los términos” (pido disculpas a los adeptos al zen por esta verbalización sin duda excesivamente occidental), y la creencia de este último cuño: “No soy más que una parte del mundo, y he de morir, y el mundo seguirá andando sin mí”.
La ciencia recibe a menudo la crítica de ser demasiado “occidental” o “dualista”, esto es, de encontrarse bajo la influencia de la dicotomía entre sujeto y objeto, o entre observador y observado. Efectivamente, hasta los comienzos de este siglo la ciencia se abocó en forma exclusiva a fenómenos que pudiesen ser distinguidos nítidamente de su observador humano: el oxígeno y el carbono, la luz y el calor, las estrellas y los planetas, aceleraciones y órbitas, etc. Esta fase fue un prólogo necesario a otra más moderna, donde la ciencia pone a la vida misma como objeto de investigación. Paso a paso, inexorablemente, la ciencia “occidental” ha ido avanzando hacia el estudio de la mente humana, lo cual equivale a decir del observador. Las indagaciones en materia de Inteligencia Artificial son el paso más reciente dado en esta ruta. Antes de la aparición de la Inteligencia Artificial en la escena, hubo dos antecedentes principales en cuanto al análisis de las curiosas consecuencias, en el campo científico, emanadas de la confusión entre sujeto y objeto. Uno consistió en la revolución de la mecánica cuántica, con su problemática epistemológica de interferencia del observador con respecto a lo observado. El otro radicó en la yuxtaposición de sujeto y objeto en metamatemática, primero a través del Teorema de Gödel y luego de otros Teoremas limitativos, a los que hemos hecho alusión. Tal vez el paso posterior al de IA sea el autoabocamiento de la ciencia: la ciencia aplicada a sí misma como objeto de estudio, lo cual significa una manera diferente de entremezclar sujeto y objeto: una manera pasible, quizá, de enredamientos mayores de los que resultan del estudio de la mente por los seres humanos mismos.
Ya que estamos, es interesante hacer notar que todas las conclusiones esencialmente subordinadas a la fusión de sujeto y objeto han sido de tipo limitativo. Además de los Teoremas limitativos, tenemos el principio de incertidumbre, de Heisenberg, según el cual la medición de una cantidad hace imposible la medición simultánea de una cantidad relacionada. Ignoro por qué todos estos resultados son limitativos; interprételo el lector como mejor le parezca.
La dicotomía sujeto objeto se vincula estrechamente con la dicotomía símbolo-objeto, explorada en profundidad por Ludwig Wittgenstein durante el primer tramo de este siglo. Más adelante, fueron adoptadas las palabras “uso” y “mención” para señalar esa misma distinción. Quine y otros, por su parte, se dedicaron extensamente a la conexión existente entre los signos y lo que éstos representan.
No solamente los filósofos se han ocupado con intensidad de esta profunda y abstracta cuestión. En nuestro siglo, tanto la música como el arte han atravesado por crisis que reflejan una honda preocupación por este problema. La música y la pintura, por ejemplo, tradicionalmente han expresado ideas o emociones mediante un vocabulario de símbolos (imágenes visuales, acordes, ritmos o elementos por el estilo); en cambio, presenciamos ahora una tendencia a explorar la capacidad de la música y del arte para no expresar cosa alguna, sino para limitarse a ser. Esto es, existir como pura pincelada, o como sonido puro, despojados de todo valor simbólico.
En música, en particular, John Cage ha alcanzado gran influencia como elaborador de una manipulación con reminiscencias zen de los sonidos. Muchas de sus composiciones transmiten un desdén por el “uso” de los sonidos —es decir, por el uso de sonidos que comuniquen estados emocionales— al propio tiempo que una regocijada “mención” de sonidos: es decir, una mezcla de yuxtaposiciones arbitrarias de sonidos, fuera de todo encuadramiento en un código previamente formulado que permitiera al oyente decodificar un mensaje. Un ejemplo típico es el “Paisaje Imaginario n.° 4”, la obra polirradio descrita en el Capítulo VI. No puedo hacer una evaluación íntegra de la obra de Cage, pero creo que gran parte de la misma ha estado dirigida a introducir la no significación en la música y, en algún sentido, a conseguir que tal no significación tenga significado. La música aleatoria se caracteriza por adentrarse en esta dirección. (Dicho al margen, la música azarosa es pariente cercana de las muy posteriores nociones de “happening” o de “arte eventual”). Muchos otros compositores contemporáneos han seguido los pasos de Cage, pero pocos de entre ellos han sido igualmente originales. Una composición de Anna Lockwood, llamada “Piano Ardiente”, consiste tan sólo en hacer restallar, con la mayor fuerza posible, cuerdas previamente estiradas al máximo; en una pieza de La Monte Young, los sonidos son obtenidos empujando el piano por todo el escenario y arremetiendo contra obstáculos con él, como si fuese un ariete.
El arte de nuestro siglo ha experimentado muchas convulsiones de índole parecida. Al comienzo fue el abandono de la representación, lo cual tuvo carácter auténticamente revolucionario, pues significó el nacimiento del arte abstracto. La obra de Piet Mondrian muestra un deslizamiento gradual desde la representación pura hasta las configuraciones más acabadamente abstractas. Después de que el mundo se hubo habituado al arte no representativo, apareció el surrealismo. Constituyó un sorprendente giro de ciento ochenta grados, algo así como el neoclasicismo musical: en el surrealismo, el arte extremadamente representativo fue “subvertido” y utilizado en función de motivos enteramente distintos: para sobresaltar, confundir, maravillar. Esta escuela fue fundada por André Bretón, y se localizó originariamente en Francia; algunos de sus miembros más conocidos fueron Dalí, Magritte, de Chirico, Tanguy.

FIGURA 137. Sentido común, de René Magritte (1945-46).

FIGURA 138. Los dos misterios, de René Magritte (1966).
De todos estos artistas, el más consciente del misterio símbolo-objeto fue Magritte (misterio que yo veo como una profunda extensión de la distinción uso-mención). Aquél la emplea para despertar respuestas intensas en los espectadores, aun cuando éstos no verbalicen dicha distinción de la manera citada. Consideremos, por ejemplo, su variación verdaderamente extraña del tema de la naturaleza muerta, cuyo título es Sentido común (figura 137). Vemos aquí una fuente con frutas, la clase de cosa ordinariamente representada en una naturaleza muerta, puesta encima de un cuadro en blanco. El conflicto entre el símbolo y lo real es notorio. Pero no acaba aquí la ironía, pues naturalmente todo el conjunto no es por sí mismo sino una pintura: en realidad, una naturaleza muerta con un tema no habitual.
La serie de cuadros de Magritte con imágenes de pipas crea fascinación y perplejidad. En Los dos misterios (figura 138), si nos circunscribimos a observar la pintura interior, recogemos el mensaje de que los símbolos y las pipas son diferentes. Luego, nuestra mirada se dirige hacia la pipa “real” que flota en el aire, más arriba, y advertimos que es real, mientras que la otra es sólo un símbolo. Sin embargo, esto es, por supuesto, totalmente erróneo: ambas yacen sobre la misma superficie plana que tenemos ante los ojos. La idea de que una de las pipas está en una pintura dos veces autoincluida, y por lo tanto es, en alguna medida, “menos real” que la otra, es enteramente una falacia. Una vez que nos hemos dispuesto a “ingresar a la habitación”, ya caímos en la trampa: hemos tomado como real la imagen. Para ser coherentes con nuestra credulidad, deberemos descender gozosamente un nivel, y confundir la imagen-dentro-de-la-imagen con la realidad. La única forma de no ser arrastrados de este modo es ver ambas pipas como simples manchas coloreadas sobre una superficie ubicada a pocos centímetros enfrente de nuestra nariz. Entonces, y exclusivamente entonces, apreciaremos la significación total del mensaje escrito: “Ceci n’est pas une pipe”… paradójicamente, sin embargo, en el instante mismo en que todo se transforma en manchas, también lo hace la inscripción, ¡y por lo tanto pierde su significación! En otras palabras: en ese instante, el mensaje verbal del cuadro se autodestruye, de una manera sumamente gödeliana.
El aire y la canción (figura 82), tomado de una serie de Magritte, logra en un nivel lo que Los dos misterios logra en dos. Mis dibujos Señal de humo y Papirotada (figuras 139 y 140), constituyen “Variaciones sobre un tema de Magritte”. Haga la prueba el lector de observar atentamente Señal de humo durante unos instantes; pronto, estará en condiciones de descifrar un mensaje oculto que reza: “Ceci n’est pas un message”. Así, si el lector descubre el mensaje, se encontrará con que éste se niega a sí mismo; pero si no lo descubre, es porque erró por completo el blanco. Debido a su indirecta autoextinción, mis dos imágenes pueden ser hechas corresponder —de modo no muy estricto— con la G de Gödel, lo cual dará origen a un “Correspompipa Central”, dentro del mismo espíritu de otros “Correspon-X Centrales”: Dogo, Cangrejo, Perezoso.
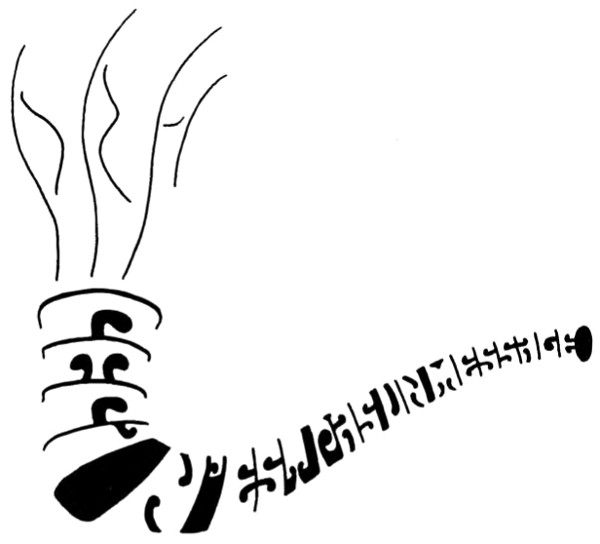
FIGURA 139. Señal de humo. [Dibujo del autor.]
Un ejemplo clásico de la confusión uso-mención en pintura lo brinda la presencia de una paleta en un cuadro. En tanto la paleta es una ilusión creada por la capacidad representativa del pintor, los colores de la paleta pintada son, literalmente, manchones de pintura extraídos de la paleta de aquél. Los colores actúan por sí mismos: no simbolizan ninguna otra cosa. En Don Giovanni, Mozart explotó un recurso parecido: introdujo explícitamente en la partitura el sonido de una orquesta afinando. De modo similar, si yo quiero que la sílaba ‘yo’ actúe por sí misma (y no que me simbolice a mí, entonces yo incluyo ‘yo’ directamente en mi texto; luego yo encierro ‘yo’ entre comillas, de lo cual resultará: “yo” (ni ‘yo’, ni tampoco “‘yo’”). ¿Está claro?

FIGURA 140. Papirotada. [Dibujo del autor.]
Un amplio número de influencias, que nadie podría detallar con precisión generaron nuevas indagaciones, en el campo del arte, del dualismo símbolo-objeto. No hay duda de que John Cage, movido por su interés en el zen, gravitó profundamente tanto en la plástica como en la música. También sus amigos Jasper Johns y Robert Rauschenberg exploraron la distinción entre objetos y símbolos mediante el empleo de objetos que actuasen como símbolos de sí mismos, o, a la inversa, haciendo que los símbolos actuasen como objetos en sí mismos. Quizá todo esto fue ensayado para destruir la noción de que el arte está situado un paso más lejos de la realidad, razón por la cual habla en “código”, lo que obliga al espectador a actuar como intérprete. La idea consistió en eliminar ese paso interpretativo y dejar al desnudo al objeto para que, simplemente, sea, punto. (“Punto”: un curioso caso de entremezclamiento uso-mención). Sin embargo, si tal fue la intención, resultó un fracaso monumental, y así debió ser, tal vez.
Toda vez que un objeto es exhibido en una galería, o recibe el calificativo de “obra”, adquiere una aura de profunda significación interior, por mucho que el espectador haya sido advertido en el sentido de que no busque significación. En realidad, se produce un efecto de culatazo en virtud del cual, cuanto más se insiste al espectador que observe estos objetos despojándose de toda perplejidad, más se le acrecienta esta última. A fin de cuentas, si un viejo cajón de embalaje apoyado en el piso de un museo es sólo un viejo cajón de embalaje apoyado en el piso de un museo, ¿por qué no viene el portero y se lo lleva, para amontonarlo con las restantes cosas de esa clase? ¿Por qué se le ha asociado el nombre de un artista? ¿Por qué ese terrón de tierra, ahí enfrente, no está también rotulado con el nombre de un artista? ¿Todo se trata de un fraude? ¿Estoy loco yo, o están locos los artistas? Más y más preguntas se acumulan en la mente del espectador, y no puede hallar la respuesta. Se trata del “efecto marco” que el arte —el Arte— crea en forma automática. No hay manera de suprimir las interrogaciones en el ánimo del curioso.
Por supuesto, si el propósito es infundir una visión de tipo zen del mundo, en tanto que desprovista de categorías y de significaciones, quizá este arte deba ser encaminado, entonces —en función de su papel intelectualizador del zen—, para que induzca catalíticamente en el espectador la tendencia a marchar hacia el conocimiento de la filosofía que rechaza las “significaciones interiores” y abarca al mundo en su conjunto. En tal caso, el arte es autodestructivo en el corto plazo, puesto que los espectadores sí estudian sus significaciones, pero este interés lo satisfacen unas pocas personas en el largo plazo, gracias a que son introducidas en las fuentes de esta modalidad artística. En este otro caso, luego, no es cierto que no exista un código que subyazca a las ideas transmitidas al espectador. En rigor de verdad, el código reside en algo aún mucho más complejo, y consiste en enunciados acerca de la ausencia de códigos, y cosas por el estilo: es decir, en parte es código, en parte es metacódigo, etc. Hay una Jerarquía Enredada en los mensajes que comunica la mayor parte de los objetos del arte de inspiración zen: tal vez sea ésta la razón por la cual tanta gente encuentre muy inescrutable el arte moderno.
Cage ha encabezado un movimiento dirigido a anular los límites entre arte y naturaleza. En música, la noción correspondiente es que todos los sonidos son iguales: una especie de democracia acústica. Así, el silencio tiene exactamente la misma importancia que los sonidos organizados. Leonard B. Meyer, en su libro Music, the Arts, and Ideas, ha denominado “trascendentalismo” a este movimiento musical, y afirma:
Si la distinción entre arte y naturaleza es errónea, la evaluación estética carece de pertinencia. No hay mayor fundamento para juzgar una sonata para piano que para juzgar una piedra, un trueno o una estrella de mar. “Los enunciados categóricos tales como correcto e incorrecto, bello y feo, típicos del pensamiento racionalista de la estética tonal”, escribe Luciano Berio [un compositor contemporáneo], “ya no son útiles para comprender por qué ni cómo un compositor actual trabaja con las formas audibles y la acción musical”.
Más adelante, Meyer expone la posición filosófica del trascendentalismo:
… todas las cosas, en todo tiempo y espacio, están inextricablemente conectadas entre sí. Todas las divisiones, clasificaciones y distribuciones asignadas al universo son arbitrarias. El mundo es un acontecimiento complejo, continuo y único.[2] [¡Remembranzas de Zenón!]
Creo que “trascendentalismo” es una denominación excesivamente abultada para este movimiento. En su lugar, yo lo llamaría “ismo”. Tratándose de un sufijo sin prefijo, sugiere una ideología sin ideas, lo cual, pese a lo que pueda interpretar el lector, quizá sea el caso. Y, puesto que “ismo” abarca lo que sea que fuere, es una denominación perfectamente adecuada. Ismo es el espíritu del zen en el campo del arte; y, así como el objetivo central del zen es el desenmascaramiento del yo, el problema central del arte de nuestro siglo parece ser el descubrimiento de qué es el arte mismo. Todos estos estremecimientos son parte de sus crisis de identidad.
Ya hemos visto que la dicotomía uso-mención, cuando es desarrollada, se transforma en el problema filosófico del dualismo símbolo-objeto, el cual, a su vez, se vincula con el misterio de la mente. A propósito de su cuadro La condición humana I (figura 141), Magritte escribió:
Frente a una ventana, vista desde el interior de una habitación, coloqué una pintura que representaba exactamente la parte del paisaje que quedaba oculta por la propia pintura. En consecuencia, el árbol representado impide la visualización del árbol situado detrás suyo, fuera de la habitación. Por así decir, el árbol existe de dos formas simultáneas en la mente del espectador: dentro del cuarto, en la pintura, y fuera del cuarto, en el paisaje real. Y esto se asemeja a la manera en que vemos el mundo: lo consideramos exterior a nosotros, pese a que no es sino una representación mental de nuestras experiencias internas.[3]

FIGURA 141. La condición humana I, de René Magritte (1933).
Primero a través de las fecundas imágenes de sus cuadros, y después con sus propias palabras, Magritte asienta la vinculación entre estas dos preguntas: “¿Cómo actúan los símbolos?” y “¿Cómo actúa nuestra mente?”. De este modo, nos devuelve al interrogante ya planteado: “¿Podemos confiar en comprender alguna vez nuestra mente/cerebro?”.
¿O habrá alguna proposición gödeliana fantásticamente diabólica que nos impida, por siempre, desenmarañar nuestras mentes? A condición de que no adoptemos una definición totalmente irrazonable de “comprensión”, no veo obstáculo gödealiano alguno en el camino hacia el logro de esa comprensión. Por ejemplo, me parece sumamente razonable el afán de comprender los principios del funcionamiento del cerebro, en general, en una forma análoga al modo en que comprendemos, en general, los principios de funcionamiento de los vehículos a motor. Esto difiere por completo del intento de comprender un cerebro individual hasta el último detalle, ¡dejemos esto a cargo de nuestro propio cerebro! No veo cómo el Teorema de Gödel, pese a lo insuperablemente resbaladizo de su construcción, tenga nada que decir a propósito de la practibilidad de aquel proyecto. No veo razón alguna para que el Teorema de Gödel imponga limitaciones a nuestra capacidad de formular y verificar la presencia de mecanismos generales, responsables de que los procesos del pensamiento tengan lugar en el ámbito de las células nerviosas. No veo que el Teorema de Gödel imponga barreras a la instrumentación, a través de computadoras (o sus sucesoras), de modalidades de manipulación de símbolos que logren, aproximadamente, los mismos resultados que logra el cerebro.
Otra cuestión, completamente distinta, es la de esforzarse por duplicar, en un programa, determinada mente humana en particular; sin embargo, producir un programa inteligente no es, en absoluto, un objetivo más limitado. El Teorema de Gödel no nos impide reproducir nuestro propio nivel de inteligencia mediante la utilización de programas, así como no nos impide la reproducción de nuestro nivel de inteligencia propio mediante la información hereditaria contenida en el ADN, seguida por la educación, hemos visto en el Capítulo XVI, ciertamente, cómo un notable mecanismo gödeliano —el Bucle Extraño de las proteínas y del ADN— ¡es precisamente lo que permite la transmisión de la inteligencia!
¿El Teorema de Gödel, entonces, no tiene absolutamente nada que aportar con respecto al estudio de nuestra mente? Creo que sí, aunque no en la forma mística y limitativa que alguna gente cree. Creo que el proceso de arribar a la comprensión de la demostración de Gödel, con su construcción que abarca códigos arbitrarios, isomorfismos complejos, niveles altos y bajos de interpretación, y la capacidad de autorreflejo, puede insuflar ciertas resonancias y corrientes subterráneas dentro de un conjunto de imágenes relativas a los símbolos, y a su procesamiento, que harán posible la profundización de las intuiciones referidas a las relaciones existentes entre las estructuras mentales de los diferentes niveles.
Antes de proponer una curiosa “aplicación” filosófica de la demostración de Gödel, me gustaría traer a colación la idea de la “inexplicabilidad accidental” de la inteligencia. Se la puede expresar así: quizá nuestro cerebro, a diferencia de los vehículos a motor, sea un sistema inabordable y cerrado, imposible de descomponer nítidamente en partes separadas. En la actualidad, no sabemos si el cerebro se prestará a la realización de repetidos intentos de seccionarlo en estratos claramente discernibles, cada uno de los cuales pueda ser explicado en función de los estratos inferiores; tampoco sabemos si, por el contrario, rechazará todos nuestros ensayos de fraccionamiento.
Pero aun cuando fracasemos en nuestro empeño de comprendernos a nosotros mismos, no es necesario pensar que ello se debe a algún “retorcimiento” gödeliano, influyendo desde las sombras; la insuficiencia de nuestro cerebro para comprenderse a sí mismo puede no ser más que un simple accidente del destino. El cerebro del tierno gorila, por ejemplo, está muy por debajo, obviamente, del nivel requerido para la autocomprensión, y sin embargo es un cerebro notablemente similar al nuestro. En realidad, es probable que el cerebro de los gorilas, elefantes, boas —incluso el de las tortugas o el de seres desconocidos mucho más inteligentes que nosotros— operen básicamente, en todos los casos, con arreglo al mismo conjunto de principios. Es posible que los gorilas se encuentren muy por debajo del umbral necesario de inteligencia que permite comprender cómo se conjugan tales principios para producir las cualidades de la mente; es posible que los seres humanos se encuentren muy próximos a ese umbral, quizá apenas por debajo del mismo, quizá, inclusive, por encima. La cuestión central es que no pueden existir razones fundamentales (esto es, gödelianas) que hagan de tales cualidades algo incomprensible: pueden ser algo perfectamente comprensible a los ojos de seres más inteligentes.
Dejando a un lado esta noción pesimista de la inexplicabilidad accidental del cerebro, ¿qué aperturas podría brindarnos la demostración de Gödel, con relación a las explicaciones de nuestra mente/cerebro? La demostración de Gödel nos aporta el criterio de que una perspectiva de alto nivel de un sistema puede contener potencialidades explicativas que, simplemente, están ausentes en los niveles más bajos. Quiero decir lo siguiente: supongamos que alguien nos presenta a G, cadena indecidible de Gödel, como cadena de TNT; supongamos asimismo que no sabemos nada de numeración Gödel. La pregunta a la que debemos dar respuesta es: “¿Por qué esta cadena no es un teorema de TNT?”. Ahora bien, ya estamos habituados a este tipo de preguntas; por ejemplo, si se nos hubiese planteado es misma pregunta con referencia a SO=O, tendríamos lista una explicación: “Su negación, ~SO=O, es un teorema”. Esto, junto con nuestro conocimiento de que TNT es coherente, proporciona una explicación de por qué la cadena presentada en un no teorema. A esto es a lo que llamo una explicación “en el nivel TNT”. Adviértase cuánto difiere con respecto a la explicación de por qué MU no es un teorema del sistema MIU; ésta deriva de la vía M, aquélla exclusivamente de la vía I.
¿Y qué sucede con G? La explicación el nivel TNT que sirvió para SO=O no sirve para G, porque G no es un teorema. Quien carezca de una visión panorámica de TNT no entenderá por qué no puede conseguir que G se ajuste a las reglas, a pesar de que, en tanto que proposición aritmética, no parece contener nada inusual. En realidad, cuando G es transformada en una cadena universalmente cuantificada, todos los casos extraídos de G, mediante la sustitución de las variables por numerales, pueden ser derivados. El único medio para explicar la no teoremidad de G es descubrir la noción de numeración Gödel, y observar a TNT en un nivel enteramente diferente. No se trata sólo de que sea dificultoso y complicado formular la explicación en el nivel TNT: es imposible. Tal explicación, sencillamente, no existe. En el alto nivel existe un género de poder explicativo que lisa y llanamente falta, en principio, en el nivel TNT. La no teoremidad de G es, por decir así, un hecho intrínseco de alto nivel. Sospecho que tal es el caso con respecto a todas las proposiciones indecidibles; es decir: todas las proposiciones indecidibles son, en rigor, un enunciado Gödel, que afirma su propia no teoremidad en cierto sistema y a través de cierto código.
Observada de esta manera, la prueba de Gödel sugiere —¡pese a que no lo demuestra en absoluto!— que puede haber alguna forma de examen de alto nivel de la mente/cerebro, la cual abarcaría conceptos que no aparecen en los niveles más bajos: aquel nivel estaría dotado de facultades explicativas que no existen —ni siquiera en principio— en los niveles inferiores. Esto significa que determinados hechos podrían ser explicados sin ninguna dificultad en el alto nivel, pero no podrían ser explicados de ningún modo en los niveles más bajos; por muy extensa y laboriosamente que fuese formulado un enunciado de bajo nivel, no explicaría el fenómeno en cuestión. Esto es análogo al hecho de que, cuando hacemos derivación tras derivación en TNT, por muy extensas y laboriosas que las forjemos nunca llegaremos a G gracias a ellas, aun cuando, en un nivel más alto, podamos ver que G es verdadera.
¿Qué son aquellos conceptos de alto nivel? Desde tiempos inmemoriales, diversos científicos y humanistas de inclinación holística o “espiritualista” vienen sosteniendo que la conciencia es un fenómeno que escapa a explicaciones articuladas en términos de componentes cerebrales; cuando menos, tenemos aquí una propuesta. Existe también la siempre enigmática noción de libre albedrío. En consecuencia, tal vez aquellas cualidades sean “emergentes”, en el sentido de que requieren interpretaciones que no pueden ser provistas exclusivamente por la fisiología. Sin embargo, es importante entender que, si estamos siguiendo la demostración de Gödel para lanzar tan atrevidas hipótesis, debemos llevar la analogía hasta su extremo. En particular, es vital recordar que la no teoremidad de G tiene una explicación… ¡no es un total misterio! Esa explicación tiene su eje en la comprensión no de un nivel por vez, sino de la forma en la cual un nivel refleja su metanivel, y de las consecuencias de tal reflejamiento. Si nuestra analogía se justifica, los fenómenos “emergentes” llegarán a ser explicables en términos de una relación entre diferentes niveles de los sistemas mentales.
Estoy convencido de que la explicación de los fenómenos “emergentes” de nuestro cerebro —ideas, esperanzas, imágenes, analogías, por ejemplo, y en último término la conciencia y el libre albedrío— están basados en cierto género de Bucle Extraño, una interacción entre niveles donde el nivel superior se extiende hacia el nivel inferior y lo afecta, y al propio tiempo es determinado por este último. En otras palabras, una “resonancia” de refuerzo recíproco entre los diferentes niveles: algo sumamente parecido a lo que ocurre con el enunciado de Henkin, el cual, limitándose a aseverar su propia demostrabilidad, termina por ser realmente demostrable. El yo se constituye como tal en el momento en que adquiere la facultad de reflejarse a sí mismo.
Esto no debe ser interpretado como una postura antirreduccionista; sólo afirma que una explicación reduccionista de la mente, para ser comprensible, debe aportar conceptos “flexibles” tales como niveles, correspondencias y significaciones. En principio, no me cabe duda de que existe una explicación del cerebro totalmente reduccionista, pero incomprensible; el problema es cómo traducirla a un lenguaje que podamos manejar. Ciertamente, no nos interesa una descripción en términos de posiciones y momentos de partículas; nos interesa una descripción que relacione la actividad neural con las “señales” (fenómenos de nivel intermedio), y que relacione las señales, a su vez, con los “símbolos” y “subsistemas”, incluido el presunto “símbolo del yo”. Este acto de traducir el hardware físico de bajo nivel al software psicológico de alto nivel tiene analogía con la traducción de enunciados teórico-numéricos a enunciados metamatemáticos. Recordemos que el cruce de niveles que tiene lugar en este punto exacto de la traducción es lo que origina la incompletitud de Gödel, y también el carácter autodemostrativo del enunciado de Henkin. Sostengo que un cruce de niveles similar es lo que genera nuestro prácticamente inanalizable sentido del yo.
Para habérnoslas con toda la compleja riqueza del sistema cerebro/ mente, tendremos que ser capaces de deslizamos cómodamente de un nivel a otro. Además, debemos admitir diversos tipos de “casualidad”: los diversos medios gracias a los cuales un acontecimiento perteneciente a un nivel de descripción puede “causar” la ocurrencia de acontecimientos en otro nivel. En ocasiones, se dirá que el acontecimiento A es “causa” del acontecimiento B por la simple razón de que uno es la traducción, en otro nivel de descripción, del restante. Otras veces, “causa” tendrá su significado habitual: causalidad física. Ambos tipos de causalidad —y tal vez algunos más— tendrán que ser admitidos en toda interpretación de la mente, pues debemos admitir causas que se propaguen hacia arriba y hacia abajo de la Jerarquía Enredada de la mentalidad, tal como ocurre en el Correspondogma Central.
A la esencia, pues, de nuestra comprensión de nosotros mismos, se incorporará la comprensión de la Jerarquía Enredada de los niveles internos de la mente. Mi posición es muy similar a la postulada por el neurocientífico Roger Sperry en su excelente artículo “Mind, Brain and Humanist Values”, del cual extraigo las siguientes citas:
En mi modelo hipotético de cerebro, el conocimiento consciente es representado como un agente causal verdaderamente real, y ocupa un lugar importante en la secuencia causal y en la cadena del control de los acontecimientos cerebrales, dentro de la cual aparece como una fuerza activa y operacional… Para decirlo más sencillamente, se recae en el problema de quién impulsa a quién dentro de la multitud de fuerzas causales que ocupan el cráneo. Es un problema, en otras palabras, de desenmarañamiento de la jerarquía de poder que rige a los agentes de control intracraneanos. Dentro del cráneo, existe todo un mundo de diversas fuerzas causales; es más, hay fuerzas dentro de fuerzas dentro de fuerzas, como no se ve en ningún espacio cúbico similar del universo que yo conozca… Para presentar resumidamente un cuento que en realidad es largo: si uno sigue trepando por la cadena jerárquica interna del cerebro, encuentra en la cima misma aquellas fuerzas organizativas globales y las propiedades dinámicas de los grandes patrones de excitación cerebral que están correlacionados con los estados mentales o actividades psíquicas… Cerca de la cúspide de este sistema jerárquico de órdenes del cerebro… encontramos ideas. El hombre, a diferencia del chimpancé, tiene ideas e ideales. En el modelo de cerebro que propongo, la potencia causal de una idea, o de un ideal, llega a ser exactamente tan real como lo son una molécula, una célula o un impulso nervioso. Las ideas generan ideas y contribuyen al desarrollo de nuevas ideas. Interactúan entre sí y con otras fuerzas mentales del mismo cerebro, de cerebros próximos y, gracias a la comunicación global que permite la vinculación a la distancia, de cerebros lejanos. Y también interactúan con lo que las rodea externamente, para producir, in toto, un avance explosivo en la evolución que deja atrás, con mucho, cualquiera de las cosas que muestre la escena evolutiva, incluyendo la aparición de la célula viva.[4]
Existe una célebre diferenciación entre discursos: el de lenguaje subjetivo y el de lenguaje objetivo. Por ejemplo. La sensación “subjetiva” de rojo, y la “objetiva” longitud de onda de luz roja. Para mucha gente, éstos parecen ser términos por siempre inconciliables. Para mí no es así. No son más inconciliables que las dos perspectivas que concita Manos dibujando, de Escher: desde “dentro del sistema”, donde las manos se dibujan entre sí, y desde fuera, donde todo está siendo dibujado por Escher. El sentimiento subjetivo de rojo emana del torbellino de la autopercepción en el cerebro; la longitud de onda objetiva responde al modo en que se ven las cosas cuando damos un paso al costado y salimos del sistema. Pese a que nadie ha podido nunca apartarse lo suficiente como para ver “el gran cuadro”, no debemos olvidar que, de todos modos, existe. Debemos recordar que las leyes físicas son las que hacen que todo eso suceda: allí, precisamente allí, en los ocultos rincones y entresijos neurales ubicados a una distancia inalcanzable para nuestros sondeos introspectivos de alto nivel.
En el Capítulo XII se sugirió que eso que llamamos libre albedrío es un resultado de la interacción entre el símbolo (o subsistema) del yo y el resto de los símbolos del cerebro. Si adoptamos la idea de que los símbolos son entidades de alto nivel a las cuales deben asignarse significaciones, podemos hacer un ensayo de interpretación de las relaciones existentes entre los símbolos, el símbolo del yo y el libre albedrío.
Un recurso que nos ha de permitir la obtención de una perspectiva provechosa de la cuestión del libre albedrío es el de remplazaría por una cuestión que considero equivalente, pero que abarca términos menos recargados. En lugar de preguntar, “¿El sistema X tiene libre albedrío?”, preguntamos: “¿El sistema X realiza elecciones?”. Mediante un estudio cuidadoso de lo que realmente queremos decir cuando decidimos describir un sistema —mecánico o biológico— en función de la capacidad de éste de efectuar “elecciones”, creo que podremos arrojar mucha luz sobre el libre albedrío. Será útil examinar algunos sistemas diversos que, bajo ciertas circunstancias, pueden inducirnos a definirlos como “ejecutores de elecciones”. Los ejemplos que aportemos al respecto han de esclarecer el significado que damos a esa expresión.
Tomemos los siguientes sistemas como paradigmas: un trozo de mármol rodando por la ladera accidentada de una colina; una minicalculadora dedicada a encontrar dígitos sucesivos de la expansión decimal de la raíz cuadrada de 2; un elaborado programa, que juega una partida corriente de ajedrez; un robot en un laberinto T (un laberinto con una sola bifurcación, al final de una de las cuales espera una recompensa); un ser humano enfrentando un dilema complejo.
Empecemos con el mármol, rodando hacia bajo, ¿ejercita elecciones? Creo que, unánimemente, diríamos que no, aun cuando nadie es capaz de predecir el itinerario que sigue, ni siquiera en cuanto a un tramo muy corto. Tenemos la impresión de que el mármol no podría haber seguido sino el camino que siguió, bajo el exclusivo impulso de las inexorables leyes de la naturaleza. En nuestra física mental articulada en bloques, por cierto nos es posible visualizar una gran cantidad de diferentes recorridos “posibles”, y lo vemos seguir solamente uno de ellos en el mundo real. En consecuencia, no podemos evitar que, en algún nivel de nuestra mente, nos parezca que el mármol ha “elegido” un recorrido en particular de entre una miríada de aquellos recorridos mentales; en algún otro nivel de nuestra mente, sin embargo, comprendemos instintivamente que la física mental es únicamente un auxilio para nuestro modelamiento interno del mundo, y que los mecanismos responsables de las secuencias físicas reales de acontecimientos no necesitan que la naturaleza atraviese un proceso análogo de elaboración previa de variantes en algún universo hipotético (el “cerebro de Dios”), para luego elegir entre ellas. De modo pues que no conferiremos la designación “elección” a este proceso, aunque reconozcamos que a veces tiene utilidad práctica utilizar esa palabra en casos como éste, a causa de su poder evocador.
Bien, ¿qué ocurre ahora con la calculadora programada para encontrar los dígitos de la raíz cuadrada de 2? ¿Y con el programa de ajedrez? Respecto a estos casos, podríamos decir que son “peñascos de lujo”, rodando por “colinas de lujo”. En realidad, los argumentos en favor de la inexistencia de elección son aquí, sin duda, más poderosos que en el caso del mármol porque, si intentamos repetir la experiencia con este último, con toda seguridad veremos que describirá un recorrido totalmente diferente en su caída; en cambio, si reprocesamos el programa raíz cuadrada de 2, obtendremos los mismos resultados una y otra vez. El mármol parece “elegir” un camino distinto en cada oportunidad, por muy exactamente que procuremos reproducir las condiciones del descenso inicial, mientras que el programa es procesado en todas las ocasiones a través de los mismos canales.
Ahora bien, en el caso de los programas de ajedrez de lujo, hay varias posibilidades. Si jugamos una partida contra ciertos programas, y luego comenzamos una segunda partida efectuando los mismos movimientos iniciales que la primera vez, estos programas harán exactamente las mismas movidas de la apertura anterior, sin dar la menor apariencia de haber aprendido nada ni de tener el menor afán de variedad. Hay otros programas que tienen recursos de aleatoriedad, los cuales brindan alguna variedad pero no como producto de anhelos profundos de ninguna clase. Tales programas pueden ser puestos a cero, con el generador interno de números aleatorios como si fuese la primera vez, y repetir esto mientras la misma partida continúa. Hay otros programas que aprenden de sus errores, y modifican su estrategia con sujeción al resultado de una partida. Tales programas no juegan del mismo modo dos veces consecutivas; por supuesto, es posible también que queramos atrasar el reloj, mediante el barrido de todas las modificaciones de la memoria que representen aprendizaje, en forma idéntica a como es puesto a cero el generador de números aleatorios, pero sería muy difícil considerar benévolo un acto semejante. Además, ¿hay alguna razón para sospechar que querríamos poder cambiar algunas de nuestras propias decisiones del pasado si hasta el último detalle —lo cual incluye, por supuesto, nuestro cerebro— fuera llevado a cero, es decir, borrón y cuenta nueva?
Pero volvamos al interrogante de si “elección” es un concepto aplicable a estas situaciones. Si los programas son sólo “peñascos de lujo rodando por colinas de lujo”, ¿efectúan elecciones, o no? Por supuesto, la respuesta ha de ser subjetiva, pero yo diría que casi exactamente las mismas consideraciones son aplicables al caso del peñasco de mármol. No obstante, tengo que agregar que el atractivo ejercido por el empleo de la palabra “elección”, aun bajo la limitación de servir solamente como adecuada y evocativa referencia sintética, llega a ser muy fuerte. El hecho de que un programa de ajedrez anticipe las diversas bifurcaciones posibles, lo cual no ocurre en absoluto con un mármol cuesta abajo, lo convierte en algo mucho más semejante a un ser animado que un programa abocado a la raíz cuadrada de 2. Pero todavía no hay aquí una autoconciencia profunda, como tampoco un sentido de libre albedrío.
Imaginemos ahora un robot dotado de un repertorio de símbolos, se lo ha ubicado en un laberinto T y no marcha hacia la recompensa sino que está preprogramado para dirigirse hacia la izquierda cuando el dígito adyacente de la raíz cuadrada de 2 es par, y hacia la derecha cuando ese valor es impar. Y este robot es capaz de modelar la situación en sus símbolos, de modo que puede observarse a sí mismo ejerciendo elecciones. Si se le preguntara, cada vez que se acerca a la T, “¿sabe usted hacia qué lado se va a dirigir en esta ocasión?”, su respuesta sería “no”. A fin de seguir adelante, entonces, activaría su subrutina “decisoria”, la cual haría la determinación de cuál es el dígito inmediatamente siguiente de la raíz cuadrada de 2, y la decisión quedaría así adoptada. Ahora bien, el mecanismo interno de la subrutina decisoria es desconocido para el robot: está representado en éste meramente como una caja negra que indica “izquierda” y “derecha” gracias a alguna misteriosa y en apariencia aleatoria regla. A menos que los símbolos del robot capten la palpitación recóndita de la raíz cuadrada de 2, con sus latidos en forma de I y de D, seguirá estando desconcertado frente a las “elecciones” que efectúa. Ahora bien, ¿este robot efectúa elecciones? Hagamos esta suposición: si estuviéramos atrapados en el interior del trozo de mármol que rueda por la ladera, y careciéramos de influencia para orientar su recorrido, ¿presumiríamos que el itinerario del mármol involucra elecciones, desde el punto de vista de nuestro intelecto humano? Por cierto que no; a menos que nuestra mente esté afectando los resultados, la presencia de los símbolos no produce ninguna diferencia.
De modo pues que introducimos una modificación en nuestro robot: haremos que sus símbolos —incluido su símbolo del yo— afecten la decisión por adoptar. Tenemos aquí un ejemplo de programa enteramente procesado bajo el imperio de la ley física, que aparentemente se aproxima con mayor profundidad que los casos anteriores a la esencia de la elección. Cuando ingresa a la escena de concepto, articulado en bloques, del robot acerca de sí mismo, comenzamos a identificarlo con el propio robot pues la situación se asemeja a las que nos tienen por protagonistas. Ya no se trata de la determinación de la raíz cuadrada de 2, donde no vemos que ningún símbolo supervise la decisión adoptada. Con toda certidumbre, si examináramos el programa del robot en un nivel sumamente localizado, lo veríamos muy similar al programa de la raíz cuadrada: es ejecutado un paso tras otro y al cabo sale el resultado, “izquierda” o “derecha”. Pero si lo examinamos en un nivel elevado, veremos que los símbolos están siendo empleados para modelar la situación y afectar la decisión. Esto altera radicalmente nuestro modo de considerar el programa; en esta etapa, ha entrado a jugar un papel la significación: la misma clase de significación que manipulamos en nuestras mentes.
Si un agente externo, ahora, propone que ‘I’ sea la siguiente elección del robot, tal propuesta será recogida y canalizada a través de la revuelta masa de los símbolos en interacción. Allí, será arrastrada inexorablemente a interactuar con el símbolo del yo, tal como una canoa es atraída por un remolino. He aquí el vórtice del sistema, donde se cruzan todos los niveles. La ‘I’ choca acá con una Jerarquía Enredada de símbolos y es llevada a subir y bajar en la escala de niveles. El símbolo del yo es incapaz de supervisar todos sus procesos internos, así que cuando emerge la decisión concreta —‘I’ o ‘D’ o algo ajeno al sistema—, éste no está capacitado para establecer de dónde ha provenido dicha decisión. A diferencia de un programa habitual de ajedrez, el cual carece de controles sobre sí mismo y, en consecuencia, de idea a propósito de la procedencia de sus movidas, este otro programa se autosupervisa y tiene idea a propósito de sus ideas, pero no puede controlar en forma completamente detallada sus propios procesos: tiene, pues, una especie de sentido intuitivo de sus funciones, y no una comprensión completa del proceso. El sentimiento de libre albedrío emana de este equilibrio entre conocimiento e ignorancia de sí mismo.
Pensemos, por ejemplo, en un escritor empeñado en transmitir ciertas ideas, presentes en él bajo la forma de imágenes mentales. No tiene ninguna certeza acerca del modo en que se han reunido esas imágenes en su mente, y realiza sucesivos experimentos en búsqueda de la expresión adecuada hasta que finalmente opta por una versión definitiva. ¿Sabe él, empero, de dónde emana todo esto? Únicamente de una forma vaga; la parte principal de las fuentes, como ocurre con la base de un témpano, permanece fuera de la vista, oculta: esto es lo que sabe el escritor.
Pensemos, si no, en un programa de composición musical, tema del que ya hablamos, preguntándonos qué nos resultaba más cómodo: denominarlo “compositor”, o considerarlo el instrumento de un compositor humano. Probablemente nos sintamos cómodos cuando el autoconocimiento, en términos de símbolos, tenga existencia dentro del programa, y cuando éste alcance ese delicado equilibrio entre conocimiento e ignorancia de uno mismo. No tiene pertinencia a este respecto el hecho de que el sistema esté siendo procesado en forma determinista; lo que nos lleva a calificarlo como “elaborador de elecciones” es la posibilidad de que nos identifiquemos con una descripción de alto nivel de los procesos que tienen lugar cuando el programa es procesado. En un nivel bajo (el del lenguaje de máquina), el programa tiene el mismo aspecto que cualquier otro; en un nivel alto (articulado en bloques), pueden emerger propiedades tales como “volición”, “intuición”, “creatividad” y “conciencia”.
La noción central es que este “vórtice” es el responsable de la cualidad de enredado, de la cualidad de gödeliano, de los procesos mentales. Hay quienes me han dicho, en alguna ocasión: “Este asunto de la autorreferencia y demás es muy gracioso y entretenido, pero ¿usted cree realmente que se trata de algo serio?”. Ciertamente que así lo creo. Pienso que será reconocido finalmente como la sustancia de IA, y el foco de todos los ensayos de comprensión del funcionamiento de la mente humana. Y es por tal razón que Gödel está tan profundamente entretejido en la trama de este libro.

FIGURA 142. Galería de grabados, de M. C. Escher (litografía, 1956).
Una ilustración asombrosamente bella, y al mismo tiempo perturbadoramente grotesca, del “ojo” ciclónico de una Jerarquía Enredada, es lo que nos ofrece Escher en su Galería de grabados (figura 142). Vemos allí una galería de cuadros, donde un joven de pie observa la pintura de un barco anclado en el puerto de una pequeña ciudad que quizá sea maltesa a juzgar por la arquitectura, en la que se destacan torrecillas, algún que otro domo y chatos techos de piedra, sobre uno de los cuales se ve a un niño sentado, descansando del calor, mientras dos pisos más abajo una mujer —quizá su madre— está asomada a una ventana de la construcción, la cual está situada directamente encima de una galería de cuadros donde un joven de pie observa la pintura de un barco anclado en el puerto de una pequeña ciudad que quizá sea maltesa… ¡¿Cómo?! hemos retomado al mismo nivel del cual partimos, pese a que la lógica íntegra dicta que ello no puede ocurrir. Vamos a trazar un diagrama que refleje lo que vemos en Galería de grabados (figura 143).
FIGURA 143. Diagrama abstracto de Galería de grabados, de M. C. Escher.
Lo que muestra este diagrama son tres variedades diferentes de la propiedad de “estar en”. La galería está físicamente en la ciudad (“inclusión”); la ciudad está artísticamente en la pintura (“reproducción”); la pintura está mentalmente en la persona (“representación”). Pero aunque este diagrama pueda parecer satisfactorio, en realidad es arbitrario porque el número de niveles exhibido es enteramente caprichoso. Veamos a continuación otra forma de representar la mitad superior (figura 144):
FIGURA 144. Una versión reducida de la figura anterior.
Hemos eliminado el nivel “ciudad”; conceptualmente era útil, pero se puede prescindir de él. La figura 144 muestra igual apariencia que el diagrama de Manos dibujando: un Bucle Extraño en dos movimientos. Las demarcaciones son arbitrarias, aun cuando nuestra mente las encuentre naturales; esto puede ser llevado a un punto mayor de acentuación mediante diagramas esquemáticos de Galería de grabados sometidos a una reducción todavía más acusada, como vemos a la figura 145.
FIGURA 145. Nueva reducción de la figura 143.
Vemos aquí exhibida la paradoja de la pintura en los términos más estrictos. Sin embargo, si la pintura está “dentro de sí misma”, ¿el joven también está dentro de sí mismo, entonces? Esta pregunta es respondida por la figura 146.
FIGURA 146. Otra forma de reducción de la figura 143.
Así tenemos aquí al joven “en el interior de sí mismo”, en un curioso sentido integrado por tres distintos sentidos de “en”.
Este diagrama nos recuerda la paradoja de Epiménides, con su autorreferencia en un movimiento, mientras que el diagrama en dos pasos se asemeja a la pareja de enunciados donde cada uno de ellos hace referencia al otro. No podemos estrechar más el bucle, pero sí ampliarlo, mediante la inserción de gran cantidad de niveles intermedios tales como “marco de la pintura”, “arcada” y “edificio”. Si procedemos así, tendremos Bucles Extraños de muchos pasos, cuyos diagramas serán isomórficos a los de Cascada (figura 5) y de Subiendo y bajando (figura 6). El número de niveles es determinado por lo que nos impresiona como “natural”, lo cual varía de acuerdo al contexto, al objetivo o al marco de la mente. Puede considerarse que los Correspon-X Centrales —Dogo, Cangrejo, Perezoso y Pipa— comprenden Bucles Extraños de tres pasos; alternativamente, pueden ser reducidos a bucles de dos o de un paso; a la vez, también pueden ser expandidos y constituirse en bucles de multitud de estadios. Percibir la presencia de un nivel es una cuestión de intuición y de preferencia estética.
Pero, ¿nosotros, los observadores de Galería de grabados, también somos arrastrados en virtud de estar escrutándola? Realmente, no. Nos las arreglamos para apartarnos de este vórtice por el hecho de encontrarnos fuera del sistema. Y cuando observamos la pintura, vemos cosas que seguramente el joven no puede ver, como por ejemplo la firma “MCE” de Escher en el “lunar” central. Pese a que este lunar tiene el aspecto de una imperfección, tal vez ésta resida en nuestras expectativas porque, en verdad, Escher no podría haber llenado esa porción del lienzo sin caer en incoherencia con respecto a las reglas a las que se ajustó para realizar la pintura. Ese centro de la espiral es —y debe serlo— incompleto. Escher podría haberlo empequeñecido a voluntad, pero no podría haberse desembarazado de él. De tal modo, nosotros, en el exterior, podemos saber que Galería de grabados es esencialmente incompleto: un hecho que el joven, en el interior, jamás puede conocer.
De esta manera, Escher nos ha brindado una parábola pictórica del Teorema de la Incompletitud, de Gödel. Y es por tal razón que Gödel y Escher constituyen hebras tan indisolublemente entretejidas en la trama de este libro.
Cuando se miran los diagramas de Bucles Extraños, no se puede evitar el recuerdo del Canon Eternamente Remontante, de la Ofrenda Musical. Un diagrama de este canon contendría seis pasos, como lo muestra la figura 147. Es lamentable que, cuando regresa a do, está una octava más alto que la exacta altura inicial. Asombrosamente, es posible efectuar un reordenamiento que permita retomar con precisión a la altura del comienzo, gracias a los llamados tonos de Shepard, un descubrimiento del psicólogo Roger Shepard. El principio de una escala basada en estos tonos aparece en la figura 148. Llevado a palabras, se trata de lo siguiente: se ejecutan escalas paralelas en varios rangos de octava diferentes. Cada nota es pulsada según una intensidad independiente y, cuando las notas suben, las intensidades se modifican. Se hace que la octava superior vaya desapareciendo gradualmente, y al mismo tiempo se va introduciendo gradualmente la octava inferior. En el momento preciso en que se estaría, normalmente, una octava más alto, las intensidades se han modificado de manera de reproducir la altura inicial… Así, se puede “ascender y ascender por siempre”, ¡y no llegar nunca más arriba! Cualquiera que disponga de un piano puede intentarlo. Esto funciona más eficazmente si las alturas son rigurosamente sintetizadas mediante un control de computadora: la ilusión obtenida de este modo es extraordinariamente completa.
FIGURA 147. El esquema de modulación hexagonal del Canon Eternamente Remontante, de Bach, forma un auténtico bucle cerrado cuando se emplean los tonos de Shepard.
Este maravilloso descubrimiento musical permite que el Canon Eternamente Remontante sea ejecutado de forma tal que retorna a reunirse consigo mismo, luego de haber “subido” una octava. Esta idea, concebida conjuntamente por Scott Kim y por mí, ha sido concretada en una grabación, mediante el empleo de un sistema musical de computadora. El efecto es muy sutil, y al mismo tiempo muy real. Es muy interesante el hecho de que el propio Bach estaba aparentemente en conocimiento, en alguna medida, de tales escalas, pues en su música es posible encontrar pasajes ocasionales que hacen uso, en forma aproximada, del principio general de los tonos de Shepard: por ejemplo, casi en mitad de la Fantasía, perteneciente a la Fantasía y Fuga en Sol menor, para órgano.
En su libro J. S. Bach’s Musical Offering, dice Hans Theodore David:
Durante todo el transcurso de la Ofrenda Musical, el lector, el ejecutante o el oyente deben buscar el Tema Real en todas sus formas. La obra íntegra, por lo tanto, es un ricercar en el original y literal sentido de la palabra.[5]
Creo que así es; no es posible llegar a ver con la necesaria profundidad dentro de la Ofrenda Musical: siempre hay otra cosa después de haberse pensado que se conocía todo. Por ejemplo, hacia el final mismo del Ricercar a seis voces, la única composición que rehusó improvisar, Bach introdujo a hurtadillas su propio nombre, repartido entre dos de las voces más altas. En la Ofrenda Musical, las cosas se diseminan en muchos niveles. Hay triquiñuelas con notas y letras; hay ingeniosas variaciones sobre el Tema del Rey; hay géneros originales de cánones; hay fugas insólitamente complejas; hay belleza y una extraordinaria profundidad emotiva; inclusive, hay regocijo, esparcido en la profusión de niveles de la obra. La Ofrenda Musical es una fuga de fugas, una Jerarquía Enredada como la de Escher y la de Gödel, una construcción intelectual que me hace presente, de una manera que no puedo expresar, la hermosa fuga a multitud de voces de la mente humana. Y es por tal razón que Gödel, Escher y Bach constituyen en este libro las tres hebras cuyo entrelazamiento forma un Eterno y Grácil Bucle.

FIGURA 148. Dos ciclos completos de una escala de tonos Shepard, anotada para piano. El volumen de cada nota es proporcional a su área; así, precisamente cuando la voz superior decrece, débilmente va ingresando una nueva voz inferior. [Impreso por programa SMUT”, de Donald Byrd.]