FIGURA 119. Problema de Bongard 51. [Tomado de: M. Bongard, Pattern Recognition (Rochelle Park, N. J.: Hayden Book Co., Spartan Books, 1970).]
Inteligencia Artificial: mirada prospectiva
DESPUÉS DE LEER el Contrafactus, me dijo un amigo: “¡Mi tío casi fue Presidente de los Estados Unidos!”. “¿De veras?”, dije. “Claro”, me contestó, “fue capitán de la torpedera PT 108”. (John F. Kennedy fue capitán de la PT 109).
De esto trata el Contrafactus. A través de la reflexión cotidiana, constantemente estamos elaborando variantes mentales de las situaciones con que nos enfrentamos, de las ideas que se nos presentan o de los hechos que suceden; dejamos intocados algunos rasgos, pero otros los “retocamos”. ¿Con cuáles rasgos hacemos esto último? ¿A cuáles ni se nos ocurre modificar? ¿Cuáles son los hechos percibidos, en algún profundo nivel intuitivo, como estrechamente relacionados con los efectivamente sucedidos? ¿De cuáles creemos que “casi” sucedieron o que “podrían haber” sucedido, aun de modo ambiguo? ¿Qué versiones alternativas de los acontecimientos emergen en nuestra mente, fuera de todo pensamiento consciente, cuando escuchamos un relato? ¿Por qué ciertas contrafactibilidades nos impresionan como “menos contrafactibles” que otras? Después de todo, es obvio que cualquier cosa que no haya sucedido no sucedió. No hay grados de “no acaecimiento”; y lo mismo vale para las situaciones “casi”. En ocasiones uno dice lamentándose. “Casi ocurrió”, y en otras dice exactamente lo mismo, pero con alivio. Sin embargo, el “casi” reside en la mente, no en los acontecimientos externos.
Estamos paseando en automóvil por un camino campestre y nos topamos con un enjambre de abejas, súbitamente, sin darnos tiempo a nada; toda la situación pasa de inmediato a ser colocada en la perspectiva de un enjambre de “repeticiones” que inundan nuestra mente. Pensaremos, seguramente, u¡por suerte la ventanilla no está abierta!” o, por el contrario: “¡desgraciadamente la ventanilla no está cerrada!”. O bien, “¡por fortuna no se me ocurrió venir en bicicleta!”, o “¡Por qué no habré pasado por aquí cinco segundos antes!”. Otras repeticiones, curiosas pero posibles: “¡Si en vez de abejas hubiesen sido ciervos, me podría haber matado al chocar con ellos!”. “Seguro que estas abejas hubieran preferido tener una colisión con una rosal”. Repeticiones más curiosas aún: “¡Lástima que estas abejas no sean billetes de banco!”. “¡Lástima que en vez de ser una sola, sea todo un enjambre!”. “Suerte que yo soy yo en lugar de ser el enjambre”. ¿Qué retocamos y qué no retocamos, y por qué?
No hace mucho, la revista The New Yorker reprodujo el siguiente pasaje, publicado por el Philadelphia Welcomat:[1]
Si Leonardo da Vinci hubiese nacido mujer, el cielorraso de la Capilla Sixtina no hubiera sido pintado.
The New Yorker hizo este comentario:
Y si Miguel Ángel hubiera sido gemelos siameses, hubiese terminado su tareas en la mitad del tiempo.
Lo destacado por el comentario de The New Yorker no es que tales contrafactibilidades sean falsas; va más allá, sugiriendo que quienquiera acaricie ideas así —las de modificar el sexo o el número de un ser humano determinado— tiene que ser alguien un tanto trastornado. Paradójicamente, sin embargo, en el mismo ejemplar apareció, sin el menor sonrojo, la oración que sigue, como conclusión de una reseña bibliográfica:
Creo que [el profesor Philipp Frank] hubiese disfrutado enormemente de estos dos libros.[2]
Pero el pobre profesor Frank ya había fallecido, y está claro que es un disparate suponer que alguien pueda leer libros luego de haber muerto. Entonces, ¿por qué no fue también ironizada esta seria afirmación? De alguna manera, en un sentido difícil de determinar, los parámetros retocados de esta oración no violan tanto nuestra noción de la “posibilidad” como los ejemplos anteriores. Hay algo que nos permite imaginar, con más facilidad en este caso que en los otros, que “todas las otras cosas permanecen igual”. ¿Pero por qué? ¿De qué se tratan los medios que nos brindan certidumbres sólidas acerca de cuándo es “razonable” y cuándo es “disparatado” efectuar retoques?
Consideremos con cuánta naturalidad nos desplazamos desde la enunciación, de valor neutro, “No sé ruso”, a la expresión desiderativa más intensa, “Me gustaría saber ruso”, luego a la exclamativa, con carga emotiva, “¡Ojalá supiera ruso!”, y por último, a la ricamente contrafáctica “Si supiera ruso, hubiera leído a Chéjov y a Lermontov en su lengua original”. ¡Qué mediocre y muerta es una mente que en una negación sólo ve una barrera opaca! Una mente viva puede ver allí un mundo abierto de posibilidades.
Creo que las situaciones “casi” y las subjuntividades inconscientemente elaboradas son representativas de parte de las más pródigas fuentes potenciales de penetración en los modos a través de los cuales los seres humanos organizan, y ordenan en categorías, su percepción del mundo. Un coformulador elocuente de este punto de vista es el lingüista y traductor George Steiner, quien dice, en su libro After Babel:
Es perfectamente posible que los centros generadores del lenguaje sean lo hipotético, lo “imaginario”, lo condicional, la sintaxis de la contrafactibilidad y de la contingencia… [Estos] hacen algo más que ocasionar perplejidades filosóficas y gramaticales. Lo mismo que las formas verbales de futuro, con las cuales se percibe que aquéllos están emparentados para formar, en conjunto, el conjunto más extenso de las “suposiciones” o “alternativas”, tales proposiciones “sí” son fundamentales para la dinámica de la emotividad humana…
Son nuestras la capacidad, la necesidad, de contradecir o “in-decir” el mundo, de imaginarlo y verbalizarlo de otra manera… Necesitamos una palabra para designar el poder y la compulsión que fuerzan al lenguaje a plantear la “otredad”… Quizá la palabra sea “alteridad”, y permita definir “lo que no es el caso”, las proposiciones contrafácticas: las imágenes y las formas de la voluntad y de la evasión que insuflamos a nuestro ser mental y gracias a las cuales elaboramos el ámbito, cambiante y en buena medida ficticio, de nuestra existencia somática y social…
Finalmente, Steiner eleva un himno contrafáctico a la contrafactibilidad:
Es inverosímil que el hombre, tal como lo conocemos, hubiese podido sobrevivir sin los recursos ficticios, contrafácticos y antideterministas del lenguaje, sin la capacidad semántica, generada y almacenada en las áreas “superfluas” de la corteza, de concebir y articular posibilidades situadas más allá del circuito de la decadencia orgánica y de la muerte.[3]
La construcción de “mundos subjuntivos” se produce en forma tan casual, tan natural, que muy difícilmente advertimos que lo estamos haciendo. Seleccionamos, dentro de nuestra fantasía, un mundo que esté próximo, en cierto sentido mental interno, al mundo real. Comparamos lo que es real con lo que percibimos como casi real. Cuando procedemos así, ganamos un tipo intangible de perspectiva acerca de la realidad. El Sr. Perezoso es un ejemplo divertido de variación con respecto a la realidad: un ser pensante despojado de la capacidad de introducirse en la subjuntividad (al menos, un ser que sostiene estar despojado de tal capacidad, ¡aunque podemos registrar que todo lo dicho por él está plagado de contrafactibilidades!). ¡Pensemos cuán inconmensurablemente más pobre sería nuestra vida mental si no tuviéramos la capacidad creativa de abandonar el cerco de la realidad para desplazamos hacia el grato “si”! Además, desde el punto de vista del estudio de los procesos humanos de pensamiento, este desplazamiento es sumamente interesante pues, por regla prácticamente general, sucede sin la menor dirección consciente, lo cual significa que la determinación del tipo de cosas que admiten desplazamiento, por oposición a las que no lo admiten, proporciona una excelente mira sobre el pensamiento inconsciente.
Una forma de avanzar en nuestra perspectiva de esta métrica mental es la de “enfrentar fuego con fuego”. Esto es cumplido en el Diálogo, donde se le requiere a nuestra “capacidad subjuntiva” que imagine un mundo donde la noción misma de capacidad subjuntiva es desplazada, por comparación con lo que esperábamos. La primera repetición instantánea subjuntiva del Diálogo —relativa a Remates y los límites del campo de juego— sólo exige un esfuerzo imaginativo enteramente habitual. En realidad, fue inspirada por una observación absolutamente corriente y casual que me hiciera una persona sentada junto a mí en un partido de fútbol. Por algún motivo, me llamó la atención, y me hizo preguntarme por qué parecía tan natural retocar esa circunstancia particular y no, digamos, el marcador del partido en ese momento. A partir de estas reflexiones, pasé a considerar otros aspectos, probablemente menos desplazables, tales como el clima, la clase de deporte y, luego, variaciones sin duda más alocadas (todo ello en el ámbito del Diálogo). Observé, con todo, que ciertos desplazamientos resultaban grandemente disparatados en una situación y muy normales en otras. Por ejemplo, a veces uno puede preguntarse espontáneamente cómo serían las cosas si la pelota tuviera una forma diferente (si uno está jugando al basquetbol con una pelota inflada a medias, pongamos por caso); otras veces, en cambio, eso no cabría en absoluto en la mente (digamos, mientras se observa un partido de fútbol por televisión).
Me pareció entonces, y me sigue pareciendo, que la desplazabilidad de un aspecto de un acontecimiento (o circunstancia) determinado depende de un conjunto de contextos autoincluidos, dentro de los cuales se percibe que sucede el acontecimiento (o circunstancia). Pueden ser provechosos aquí los términos constante, parámetro y variable, tomados de la matemática. Es frecuente que tanto matemáticos como físicos y otros especialistas desarrollen un cálculo, diciendo “c es una constante, p es un parámetro y v es una variable”. Ello significas que cualquiera de estos elementos puede variar (incluida la “constante”); sin embargo, hay una jerarquía de la variabilidad. En la situación representada por los símbolos, c establece una condición global; p establece una condición un tanto menos global, la cual puede variar en tanto c no se modifique; finalmente, v puede variar en tanto c y p se mantengan fijos. Tiene escaso sentido pensar en mantener fija a v en tanto c y p varían, pues c y p establecen el contexto dentro del cual v adquiere significado. Por ejemplo, imaginemos a un dentista con su lista de pacientes y, para cada paciente, una lista de dientes. Tiene pleno sentido (y elevados honorarios) mantener fijo al paciente y variar sus dientes, pero no tiene ningún sentido mantener fijo un diente y variar el paciente. (Pese a que, en ocasiones, tendría mucho sentido variar de dentista…).
Nuestra representación mental de una situación es construida estrato por estrato. El más bajo establece el aspecto más profundo del contexto: a veces, se encuentra tan abajo que no puede variar en absoluto; por ejemplo, la tridimensionalidad de nuestro mundo está tan incorporada que a la mayoría de las personas jamás se le ocurriría desplazarla mentalmente. Es una constante constante. Luego, hay estratos que establecen transitoria, no permanentemente, rasgos fijos de situaciones, a los cuales se puede denominar supuestos de base: son las cosas que, en el fondo de nuestra mente, sabemos que pueden variar pero, así y todo, son aceptadas por regla general como rasgos inmutables. También se los puede llamar “constante”; por ejemplo, con respecto a un encuentro de fútbol, las reglas del juego son constantes de este tipo. Tenemos después los “parámetros”: hay que considerarlos más variables, pero aceptarlos transitoriamente como constantes; en un partido de fútbol, son parámetros el clima, el equipo contrario, etc.; puede haber —probablemente haya— diversos estratos de parámetros. Por último, llegamos a los aspectos más “tambaleantes” de nuestra representación mental de la situación: las variables. Se trata de las cosas tales como la jugada de Remates en los límites del campo, a las cuales se “desata” mentalmente, y no se tiene inconveniente en desplazar más allá de sus valores reales, durante un breve lapso de tiempo.
La palabra marco está de moda actualmente en IA, y puede ser definida como instrumentación computacional de un contexto, expresión acuñada, lo mismo que muchas ideas a propósito de marcos, por Marvin Minsky, pese a que el concepto genérico existe desde hace un buen número de años. En lenguaje marco, se puede decir que las representaciones mentales de situaciones involucran marcos incluidos unos dentro de otros. Cada uno de los diversos ingredientes de una situación tiene su propio marco.
Sería interesante que explicite una de mis imágenes mentales a propósito de marcos autoincluidos. Supongámonos frente a un gran número de muebles del tipo de las cómodas con cajones. Cuando elegimos una cómoda, contamos con un marco, y los huecos donde van los cajones son los sitios adecuados para incorporar “submarcos”. Ahora bien, los submarcos son, a su vez, cómodas con cajones; entonces, ¿cómo introducir una cómoda con cajones completa en el hueco previsto para un solo cajón dentro de otra cómoda con cajones? Es sencillo: se encoge y distorsiona la segunda cómoda puesto que, al fin y al cabo, esto es enteramente mental, no material. Asimismo, en el marco exterior puede haber diversos huecos para cajones que deben ser llenados; luego, puede ser necesario ocupar los huecos de algunas de las cómodas interiores (o submarcos). Y así siguiendo, recursivamente.
La vívida imagen surrealista de comprimir y aplastar una cómoda de modo que pueda amoldarse a un receptáculo de forma arbitraria es, tal vez, muy importante, pues insinúa que nuestros conceptos son comprimidos y aplastados por los contextos en los cuales los obligamos a ingresar. Así, ¿en qué se convierte nuestro concepto de “persona” cuando las gentes que consideramos son jugadores de fútbol? Seguramente se tratará de un concepto distorsionado, implantado forzadamente en nosotros por el contexto global. Hemos introducido el marco “persona” en un hueco del marco “partido de fútbol”. La tesis de representar el conocimiento a través de marcos reposa en la idea de que el mundo consiste en subsistemas cuasi contiguos, cada uno de los cuales puede servir de contexto a otros sin sufrir una excesiva desorganización, o sin generar una excesiva desorganización durante el proceso.
Una de las nociones principales en materia de marcos es que cada uno de éstos viene provisto de su propio juego de expectativas. La imagen gráfica correspondiente nos mostraría a cada cómoda con un cajón introducido, aunque flojamente ajustado, en cada agujero: ese cajón recibe el nombre de sustituto. Si se nos dice, “Dibuje el margen de un río”, elaboraremos una imagen visual dotada de diversos rasgos, la mayoría de los cuales serían omitidos si se hubiesen agregado a la primera indicación otras adicionales, como por ejemplo “durante una sequía” o “en Brasil” o “sin remolinos”. La existencia de valores sustitutos permite que el proceso recursivo de rellenar los huecos pueda finalizar. En efecto, decimos: “Vamos a completar por nosotros mismos los agujeros en una extensión de tres estratos; más allá, apelaremos a las opciones subsidiarias. “Junto con las expectativas subsidiarias, un marco contiene el conocimiento de sus límites de aplicación y recursos heurísticos para deslizarse hacia otros marcos en el caso de que haya sido ensanchado por encima de sus límites de tolerancia.
La estructura autoincluida de un marco brinda un medio para amplificar y examinar pequeños detalles desde la menor distancia que se desee: basta con dirigir el “zoom” sobre el submarco adecuado, luego sobre uno de sus submarcos, etc., hasta que se obtiene el volumen deseado de detallamiento. Es como tener un atlas de carreteras continental de AL que incluye, primero un mapa de todo el continente, luego un mapa de cada país, y en su interior mapas de cada región, y luego mapas de las ciudades y hasta de los pueblos más grandes, si es que uno necesita esos detalles. Es posible imaginar un atlas provisto de un volumen discrecional de detalles, que llegue a abarcar bloques urbanos, casas, habitaciones, etc. Se trata de silgo similar a la utilización de un telescopio con lentes de diferente poder: cada lente tiene su propio uso. Es importante que se pueda emplear toda la variedad de escalas, pues a menudo el detalle es no pertinente y hasta diversionista.
A causa de que marcos diferentes pueden ser arbitrariamente introducidos en los receptáculos de otros marcos, existen grandes posibilidades de conflicto o “colisión”. El esquema primorosamente nítido de un solo conjunto global de estratos de “constantes”, “parámetros” y “variables” es una ultrasimplificación. En realidad, cada marco tendrá su propia jerarquía de variabilidad, y esto es lo que lo habilita para analizar de qué modo percibimos un acontecimiento tan complejo como un partido de fútbol, con su gran cantidad de submarcos, subsubmarcos, etc.: una operación increíblemente complicada. ¿Cómo accionan entre sí todos estos marcos? ¿Cómo se resuelve el conflicto existente cuando un marco dice, “Este ítem es una constante”, y otro marco dice, “No, es una variable”? Éstos son problemas profundos y difíciles de teoría del marco, para los cuales no tengo respuesta. Ocurre también que no hay todavía un completo acuerdo a propósito de qué es realmente un marco, ni de cómo se los ha de instrumentar dentro de los programas IA. Voy a hacer un intento propio de examen de dichas cuestiones en la sección que sigue, donde comento algunos acertijos relativos a reconocimiento de patrones visuales, a los cuales llamo “problemas de Bongard”.
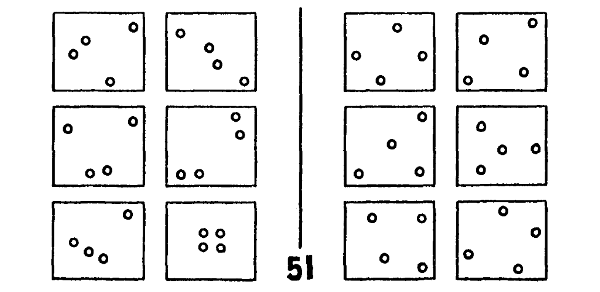
Los problemas de Bongard (PB) son los que se ajustan al tipo general propuesto por el científico ruso M. Bongard, en su libro Pattern Recognition. Un PB típico —el número 51 dentro de su colección de un centenar— es mostrado en la figura 119.

FIGURA 119. Problema de Bongard 51. [Tomado de: M. Bongard, Pattern Recognition (Rochelle Park, N. J.: Hayden Book Co., Spartan Books, 1970).]
Estos fascinantes problemas son planteados a los reconocedores de patrones, ya humanos, ya mecánicos. (También se los podría aplicar en IET: inteligencias extraterrestres). Cada problema consiste en doce figuras con forma de cajas (llamadas cajas, de aquí en más): seis a la izquierda, integrando la Clase II, y seis a la derecha, integrando la Clase II. Las cajas pueden ser indicadas de la siguiente forma:
|
I-A |
I-B |
II-A |
II-B |
|
I-C |
I-D |
II-C |
II-D |
|
I-E |
I-F |
II-E |
II-F |
El problema es: “¿En qué difieren las cajas de la Clase I de las cajas de la Clase II?”.
Un programa de resolución de problemas Bongard tendrá varios estadios, a través de los cuales los datos en bruto se van convirtiendo paulatinamente en descripciones. Las primeras etapas son relativamente inflexibles, en tanto que las más elevadas pasan a ser, poco a poco, más flexibles. Los estadios finales cuentan con una propiedad a la que denomino tentatividad, lo cual significa simplemente que el modo en que es representada una imagen es siempre tentativa. Si así parece convenir, puede ser restructurada toda una descripción de alto nivel mediante la utilización de los recursos aportados por las etapas más avanzadas.
Las ideas presentadas a continuación tienen también una cualidad tentativa. Trataré de transmitir, primero, criterios globales, y de comentar las dificultades significativas; luego, volveré atrás y procuraré explicar sutilezas, artificios, etc. De modo, pues, que la noción del lector acerca de cómo funciona todo esto puede también experimentar revisiones a medida que vaya leyendo. Pero ello forma parte del espíritu de esta exposición.
Supongamos, entonces, que enfrentamos un problema de Bongard que queremos resolver. El problema es presentado a una cámara de televisión y los datos en bruto quedan definidos. Luego, estos últimos son preprocesados, lo cual significa que son detectados determinados rasgos salientes. Los nombres de estos rasgos constituyen un “minivocabulario” del problema; son extraídos de un “vocabulario de rasgos salientes” más general. Algunos términos habituales de este último son los siguientes:
segmento lineal, curva, horizontal, vertical, negro, blanco, grande, pequeño, puntiagudo, redondo…
En una segunda etapa del preprocesamiento, son utilizados algunos conocimientos sobre formas elementales; si se encuentra alguna de éstas, su nombre también pasa a ser disponible. En consecuencia, pueden ser seleccionados términos tales como:
triángulo, círculo, cuadrado, depresión, protuberancia, ángulo recto, vértice, punta, flecha…
Éste es aproximadamente el punto donde, en los seres humanos, se encuentran lo consciente y lo inconsciente. El interés principal de esta exposición es la descripción de lo que sucede de aquí en adelante.
Ahora que la imagen ha sido “comprendida”, en alguna medida, en función de conceptos familiares, se puede examinar las perspectivas. Las descripciones tentativas se refieren a una o algunas de las doce cajas. Normalmente, utilizarán descripciones simples, como por ejemplo:
arriba, abajo, a la derecha de, a la izquierda de, dentro, fuera de, junto a, lejos de, paralelo a, perpendicular a, en fila, diseminado, regularmente espaciado, irregularmente espaciado, etc.
Pueden emplearse también descriptores numéricos definidos e indefinidos:
1, 2, 3, 4, 5,… muchos, pocos, etc.
Es posible elaborar descriptores más complicados, como por ejemplo:
más a la derecha de, menos próximo a, casi paralelo a, etc.
De tal manera, una caja ordinaria —digamos la I-F del PB 47 (figura 120)— puede ser descrita diversamente en función de que presenta:
tres formas
o
tres formas blancas
o
un círculo a la derecha
o
dos triángulos y un círculo
o
dos triángulos apuntando hacia arriba
o
una forma grande con dos formas chiquitas
o
una forma en curva con dos formas rectilíneas
o
un círculo con formas similares en su interior y exterior

FIGURA 120. Problema de Bongard 47. [Tomado de: M. Bongard, Pattern Recognition.]
Cada una de estas descripciones ve la caja a través de un “filtro”. Fuera de contexto, cualquiera de aquéllas puede ser una descripción útil. Tal como aparecen, sin embargo, todas son “erróneas”, en el contexto del problema Bongard específico del cual son parte. En otras palabras, si uno conoce la distinción entre Clases I, II, del PB 47, y se le presenta una de las líneas precedentes como descripción de una figura fuera de la vista, esa información no posibilitará la determinación de cuál es la Clase a la que pertenece dicha figura. El rasgo esencial de esta caja, en contexto, es que incluye
un círculo que contiene un triángulo.
Cabe hacer notar que quien hubiese oído una descripción semejante no estaría en condiciones de reconstruir el dibujo original, pero sí de reconocer los dibujos que cuenten con esa propiedad. Es algo un tanto análogo al estilo musical: se puede ser un reconocedor infalible de Mozart y al mismo tiempo incapaz de componer nada que impresione como propio de Mozart.
Consideremos ahora la caja I-D PB 91 (figura 121). Una descripción recargada, pero “correcta” en el contexto de PB 91, es la siguiente:
un círculo con tres muescas rectangulares.
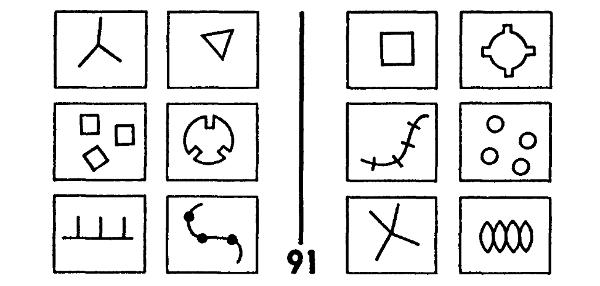
FIGURA 121. Problema de Bongard 91. [Tomado de: M. Bongard, Pattern Recognition.]
Obsérvese cuán elaborada es esta descripción, en la cual la palabra “con” cumple una función denegatoria, al implicar que el “círculo” no es realmente un círculo: es casi un círculo, salvo que… Además, las muescas no son rectángulos completos. Hay una gran extensión de “juego” en la forma en que usamos el lenguaje para describir cosas. Evidentemente, ha sido descartado un montón de información y podría descartarse una porción mayor aún. Es muy difícil saber a priori qué corresponde desechar y qué corresponde retener; por lo tanto, es necesario codificar algún género de método, por vía heurística, que permita una conciliación inteligente de aquellas dos tendencias. Por supuesto, siempre existe la posibilidad de recurrir a los niveles de descripción más bajos (es decir, a las descripciones menos articuladas en bloques), si la información descartada debe ser recuperada: es similar al caso de las personas, que pueden examinar constantemente el acertijo para ayudarse a restructurar sus ideas acerca del mismo. El recurso, entonces, es idear reglas explícitas que indiquen cómo hacer para:
Una estrategia excelente consistiría en tratar de efectuar descripciones que sean estructuralmente similares entre sí, en la medida de lo posible. Cualquier estructura que las descripciones tengan en común hará mucho más fácil su comparación. Dos elementos importantes de esta teoría se ocupan de tal estrategia; uno, es la idea de “esquemas de descripción”, o moldes; la otra es la idea de Desi: un “detector de similitud”.
Empecemos por este último. Desi es un agente especial, presente en todos los niveles del programa. (En realidad, puede haber diferentes clases de Desi en los diferentes niveles). Desi se filtra constantemente dentro de las descripciones individuales y de las descripciones diferentes, a la búsqueda de descriptores u otras cosas que se repitan. Cuando es descubierta alguna similitud, son varias las operaciones de restructuración que pueden ser desencadenadas, ya en el nivel de la descripción individual, ya en el nivel de diversas descripciones simultáneas.
Veamos ahora los moldes. Lo primero que tiene lugar después del preprocesamiento es un esfuerzo por elaborar un molde, o esquema de descripción: un formato uniforme para aplicar a las descripciones de todas las cajas de un problema. Se toma como base que, por lo común, puede fragmentarse una descripción, de modo natural, en subdescripciones, y éstas a su vez en subsubdescripciones, si es necesario. Se llega al límite inferior cuando se entra en contacto con los conceptos iniciales, pertenecientes al nivel del preprocesador. Ahora bien, es importante optar por una forma de dividir la descripción en partes que reflejen lo que sea común a todas las cajas; de otro modo, estaremos introduciendo en el mundo un “seudo orden” superfluo y carente de sentido.
¿Qué información fundamenta la construcción de un molde? Lo mejor será analizar un ejemplo. Veamos el PB 49 (figura 122); el preprocesamiento produce la información de que cada caja consiste en varias oes pequeñas, y una gran curva cerrada. Ésta es una observación valiosa, que merece ser incorporada al molde. Así un primer ensayo de molde sería:
Es muy simple: el molde-descripción tiene dos huecos dentro de los cuales han de ser introducidas las subdescripciones.
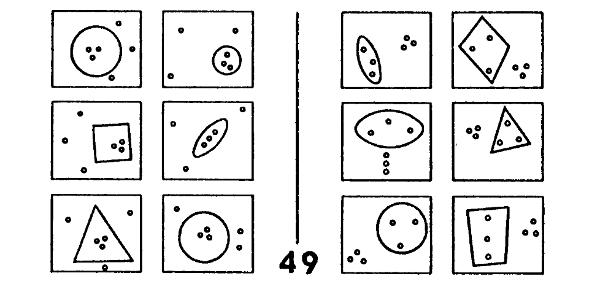
FIGURA 122. Problema de Bongard 49. [Tomado de: M. Bongard, Pattern Recognition.]
Señalemos que ocurre una cosa interesante, desencadenada por la expresión “curva cerrada”. Uno de los módulos más importantes del programa es un tipo de red semántica —la red conceptual—, en la cual todos los sustantivos, adjetivos, etc, conocidos, están vinculados en formas que indican sus interrelaciones. Por ejemplo, “curva cerrada” está fuertemente vinculada con los términos “interior”. La red conceptual prácticamente rebosa de información acerca de las relaciones entre términos, tales como cuáles son opuestos, cuáles son similares, cuáles suelen aparecer coincidentemente, etc. Una reducida porción de una red conceptual, explicada brevemente más adelante, puede verse en la figura 123. Pero ahora continuemos con lo que sigue, a propósito de la solución del problema 49. Los conceptos “interior” y “exterior” son activados por su proximidad, en la red, respecto a “curva cerrada”. Esto sugiere al constructor del molde que podría ser una idea acertada la de prever huecos distintos para el interior y el exterior de la curva. Así, dentro del espíritu de la tentatividad, el molde es tentativamente reestructurado de esta manera:
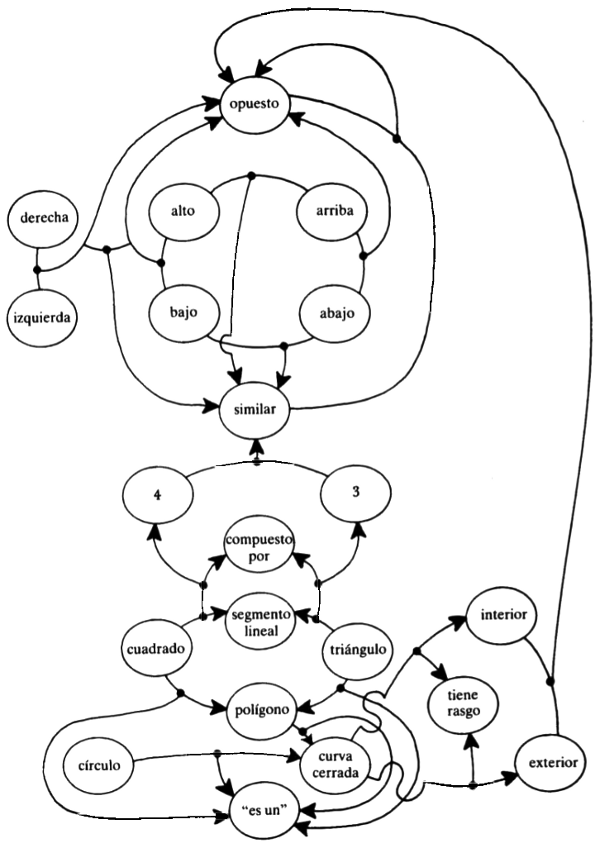
FIGURA 123. Una pequeña porción de una red conceptual de un programa destinado a resolver problemas de Bongard. Los “nódulos” son asociados mediante “enlaces”, que a su vez pueden ser enlazados. Si se considera como verbo a un enlace, y a los nódulos que éste asocia como sujeto y objeto, es posible extraer ciertas oraciones de este diagrama.
Ahora bien, cuando sean procuradas las subdescripciones, los términos “interior” y “exterior” generarán procedimientos de inspección de aquellas regiones específicas de la caja. Lo hallado en PB 49, caja I-A, es lo siguiente:
Y una descripción de la caja II-A del mismo PB podría ser así:
Desi, por su parte, en constante actividad en paralelo con otras operaciones, advierte la recurrencia del concepto “tres” en todos los huecos relacionados con oes, lo cual importa una razón de peso para emprender una segunda operación restructuradora del molde. Tómese nota de que la primera fue sugerida por la red conceptual, la segunda por Desi. Nuestro molde del problema 49 pasa entonces a ser ahora el siguiente:
Ahora que “tres” ha alcanzado un nivel generalidad —es decir, con su incorporación al molde— adquiere importancia la exploración de sus aledaños en la red conceptual. Allí encontramos “triángulo”, de lo cual se desprende que los triángulos de oes pueden ser significativos. Cuando así ocurre, ello conduce a un callejón sin salida, pero, ¿cómo saberlo por anticipado? Es un típico callejón sin salida, que un ser humano exploraría, ¡de modo que será adecuado si nuestro programa lo encuentra adecuado! Podría ser generada una descripción como la que sigue, para la caja II-E:
Por supuesto, ha sido descartada una enorme cantidad de información relativa a las dimensiones, posición y orientación de esos triángulos, además de muchas otras cosas. ¡Pero en esto reside toda la cuestión de optar por la elaboración de descripciones en lugar de la sola utilización de los datos en bruto! Se trata de la misma noción de embudamiento canalizados de la que hablamos en el Capítulo XI.
No nos es necesario presentar la solución completa del problema 49; basta con mostrar la permanente interacción, ejercida en todas direcciones, de las descripciones individuales, los moldes, el detector de similitud y la red conceptual. Deberíamos ahora examinar con mayor atención esta última y sus funciones. Una porción simplificada, de las que muestra la figura, codifica las siguientes ideas:
Adviértase que se puede hablar de todo lo que integra la red, sean nódulos o enlaces; en este sentido, ningún elemento de la red está ubicado en un nivel superior a ningún otro. La otra porción de la red, mostrada por la figura, codifica las siguientes ideas:
La red de conceptos es, por fuerza, muy vasta; aparentemente, se limita a almacenar conocimientos de modo estático, o declarativo, pero esto no es más que la mitad del cuento. En realidad, ese conocimiento se acerca también a la condición procedimental, por el hecho de que las proximidades dentro de la red actúan como guías, o “programas”, que indican al programa principal cómo desenvolver su comprensión de los dibujos inscriptos en las cajas.
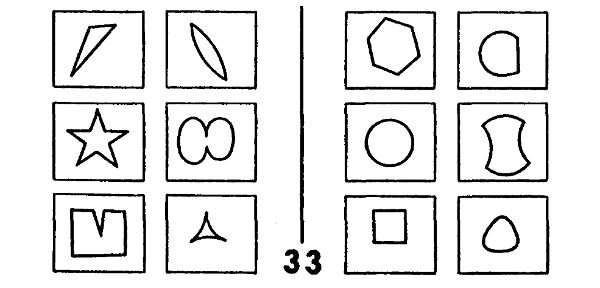
FIGURA 124. Problema de Bongard 33. [Tomado de: M. Bongard, Pattern Recognition.]
Por ejemplo, un primer empeño puede resultar equivocado y, sin embargo, quizá contenga el germen de la respuesta correcta. En PB 33 (figura 124), es posible comenzar precipitándose a la conclusión de que las cajas de Clase I contienen formas “puntiagudas”, y las de la Clase II, formas “redondeadas”. Bajo un examen más minucioso, tal cosa se revela errónea; sin embargo, hay en ello una penetración valiosa que puede ser profundizada mediante el deslizamiento, en la red, hacia los conceptos que parten de “puntiagudo”. Un concepto contiguo es el de “agudo”, que es precisamente el rasgo distintivo de la Clase I.
De tal modo, una de las principales funciones de la red conceptual es permitir que las conjeturas erróneas sean ligeramente modificadas gracias a su deslizamiento hacia variaciones que pueden ser correctas.
Esta noción de deslizamiento entre términos estrechamente relacionados se conecta con la que considera a un objeto determinado como variación de otro objeto. Un acertado ejemplo de esto ya ha sido mencionado: el del “círculo con tres muescas”, aplicado a algo que no es en absoluto un círculo. Uno tiene que ser capaz de contraer los conceptos, cuando es adecuado hacerlo. Nada ha de ser absolutamente rígido. Por otro lado, sin embargo, las cosas no deben diluirse tanto que nada conserve el menor significado. La solución estriba en saber cuándo y cómo deslizarse de un concepto a otro.
Un juego de ejemplos sumamente interesante, donde el deslizamiento de una descripción a otra constituye lo esencial del asunto, es aportado por los problemas de Bongard 85 a 87 (figura 125). El PB 85 es bastante trivial; supongamos que nuestro programa identifica “segmento lineal” en su etapa de preprocesamiento; será entonces relativamente simple para él contar segmentos lineales y arriba a la diferencia existente entre la Clase I y la Clase II, en PB 85. Vamos ahora al PB 86; éste emplea una heurística general, consistente en someter a prueba ideas que han funcionado recientemente. La repetición exitosa de métodos recientes es muy común en el mundo real, y Bongard no trata de ser más listo que este tipo de heurística en su colección: en realidad, afortunadamente, la refuerza. De modo que nos sumergimos sin demora en el problema 86 con dos ideas (“contar” y “segmentos lineales”), fusionadas en una sola: “contar segmentos lineales”. Pero sucede que el truco de PB 86 es contar sucesiones lineales, y no segmentos lineales, donde “sucesión lineal” significa una concatenación punta con punta de (uno o más) segmentos lineales. Una forma de que el programa pueda determinar esto es que tanto el concepto de “sucesión lineal” como el de “segmento lineal” sean conocidos, y que sean contiguos dentro de la red conceptual. Otra forma es que invente el concepto de “sucesión lineal”: una sugerencia capciosa, para decir lo menos.
Tenemos luego el PB 87, en el cual es llevada más allá la noción de “segmento lineal”. ¿Cuándo un segmento lineal es tres segmentos lineales? El programa debe ser lo suficientemente flexible como para que pueda trasladarse de una parte a otra entre tales representaciones diferentes de una parte determinada de un dibujo. Es conveniente almacenar las representaciones anteriores, en lugar de olvidarlas y verse luego quizá en la necesidad de reconstruirlas, pues nada garantiza que una representación más reciente sea mejor que una anterior. Así, junto con cada representación anterior han de almacenarse algunas de las razones existentes para aprobarla o desaprobarla. (Esto comienza a parecer bastante complejo, ¿verdad?).
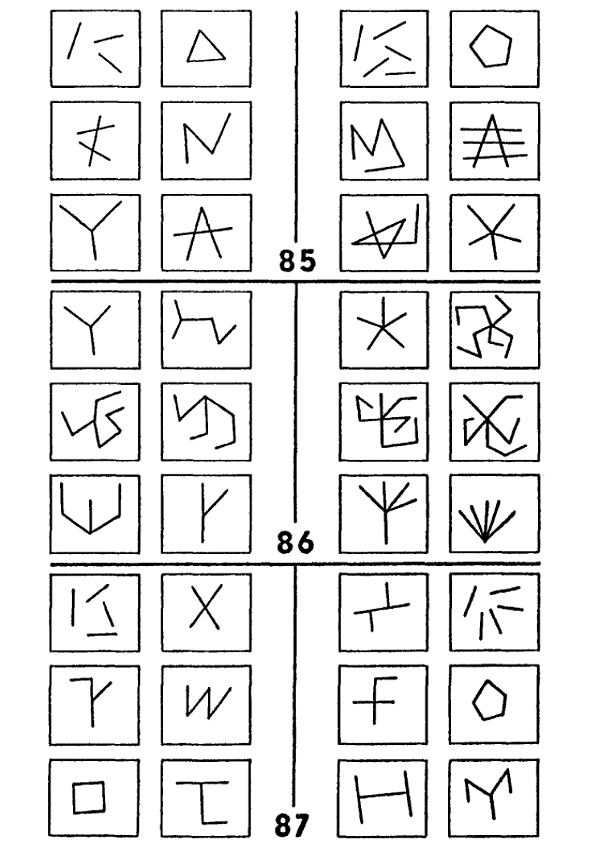
FIGURA 125. Problema de Bongard 85 a 87. [Tomado de: M. Bongard, Pattern Recognition.]
Llegamos ahora a otra parte vital del proceso de reconocimiento, relacionado con niveles de abstracción y con metadescripciones. Es de aplicación aquí el PB 91 (figura 121), ya considerado en parte. ¿Qué clase de molde puede ser construido en este caso? Hay tal volumen de variedad que es dificultoso saber por dónde empezar. ¡Pero ese hecho mismo constituye una pista! La pista dice, específicamente, que muy probablemente la distinción de clase repose en un nivel de abstracción más alto que el de la descripción geométrica. Esta observación le señala al programa que debe construir descripciones de descripciones; esto es, metadescripciones. En este segundo nivel, tal vez emerja algún rasgo común; y, si tuviéramos suerte, ¡descubriríamos la comunidad suficiente como para guiamos hacia la formulación de un molde para aplicar a las metadescripciones! Por lo tanto, nos lanzamos adelante sin un molde y elaboramos descripciones de varias cajas; luego, una vez listas las descripciones, las describimos. ¿Qué clases de huecos tendrá nuestro molde de metadescripciones? Quizá éstos, entre otros:
Hay muchos tipos de huecos que pueden resultar necesarios en la metadescripción, pero esto es un ejemplo. Supongamos ahora que hemos descripto la caja I-E del PB 91. Esa descripción (sin molde) podría ser más o menos así:
Por cierto, ha sido descartada gran cantidad de información: el hecho de que las tres líneas verticales tengan la misma extensión, de que estén espaciadas en forma equidistante, etc. Pero es positivo que se haya obtenido esta descripción. Luego, la metadescripción podría tener esta apariencia:
No es necesario que sean llenados todos los huecos de las metadescripciones; en este nivel, la información puede ser descartada tal como lo es en el nivel de la descripción directa.
Ahora bien, si tuviéramos que hacer la descripción de cualquiera de las otras cajas de la Clase 1, y luego su metadescripción, terminaríamos llenando el hueco “repeticiones en la descripción”, en cada oportunidad, con la expresión “3 ejemplares de…”. Esto sería advertido por el detector de similitud, el cual seleccionaría la trinidad como rasgo saliente, ciertamente en un alto nivel de abstracción, de las cajas de la Clase 1. De modo similar, la cuaternidad sería reconocida, por vía del método metadescriptivo, como la marca de la Clase II.
Con todo, puede objetarse que, en este caso, la apelación al método de la metadescripción es como dispararle a una mosca con un rifle de cazar elefantes, pues la trinidad y la cuaternidad podrían haber sido mostradas con igual facilidad, en el nivel inferior, si hubiéramos construido nuestras descripciones de modo ligeramente distinto. Sí, es verdad, pero es importante contar con la posibilidad de resolver estos problemas a través de diferentes rutas. Tiene que haber un amplio margen de flexibilidad en el programa, y es necesario no reprimirlo en el caso de que, malafóricamente hablando, nos lleve a “tomar el rábano por las ramas” durante cierto lapso. (La graciosa expresión “maláfora”” fue acuñada por el periodista Lawrence Harrison: surge del cruce entre un “malogro” y una “metáfora”. Es un excelente ejemplo de “recombinación de ideas”). De todos modos, me interesaba ilustrar el principio general que dice: Cuando es difícil construir un molde porque el preprocesador encuentra un exceso de diversidad, ello servirá como indicio de que los conceptos están involucrados en un nivel de abstracción más alto que el conocido por el preprocesador.
Nos ocuparemos ahora de otro problema: el de los modos a través de los cuales se descarta información. Esto toca dos nociones interrelacionadas, a las que denomino “enfocamiento” y “filtrado”. La primera consiste en una descripción cuyo foco es cierta parte del dibujo inscripto en la caja, con exclusión de toda otra cosa. La segunda consiste en una descripción que se concentra en cierta forma específica de examinar el contenido de la caja, e ignora deliberadamente todo otro aspecto. Así, ambas nociones son complementarias: el enfocamiento se aplica a los objetos (a los sustantivos, poco más o menos), y el filtrado a los conceptos (a los adjetivos, poco más o menos). Para ejemplificar el enfocamiento, analicemos el PB 55 (figura 126): enfocamos aquí el amuescamiento y el pequeño círculo aledaño, con exclusión de toda otra cosa que hay en la caja. El PB 22 (figura 127) nos ofrece un ejemplo de filtrado: aquí, debemos filtrar todos los conceptos que no sean el de tamaño. Para resolver el PB 58 (figura 128), se requiere una combinación de enfocamiento y filtrado.
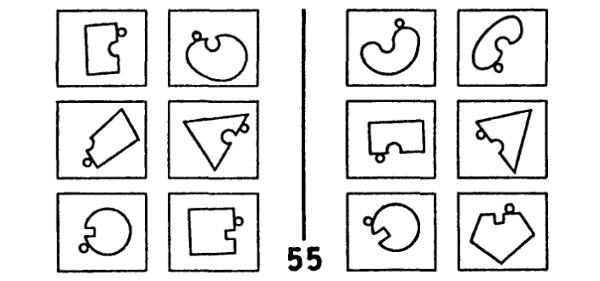
FIGURA 126. Problema de Bongard 55. [Tomado de: M. Bongard, Pattern Recognition.]
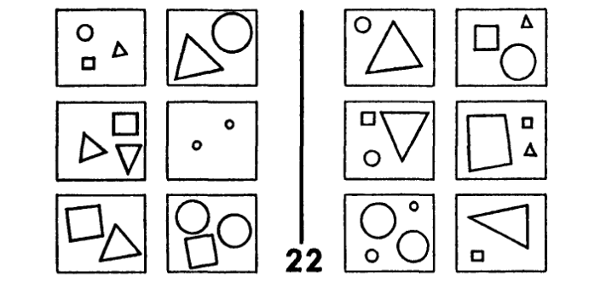
FIGURA 127. Problema de Bongard 22. [Tomado de: M. Bongard, Pattern Recognition.]
Uno de los recursos más importantes para obtener criterios que faciliten el enfocamiento y el filtrado es provisto por otro género de “enfocamiento”: a saber, la inspección de una sola caja particularmente simple, digamos una que contenga la menor cantidad de objetos que sea posible; puede ser muy útil comparar las cajas más despobladas de las dos Clases, ¿pero cómo establecer cuáles son las cajas despobladas hasta que no se disponga de su descripción? Bueno, un medio es el de buscar una caja que tenga un mínimum de los rasgos suministrados por el preprocesador. Esto puede ser realizado en los comienzos, pues no exige un molde preexistente; en realidad, es algo que puede constituirse en una manera provechosa de descubrir rasgos que permitan construir una molde. El PB 61 (figura 129) ejemplifica la posibilidad de que esa técnica conduzca rápidamente a una solución.
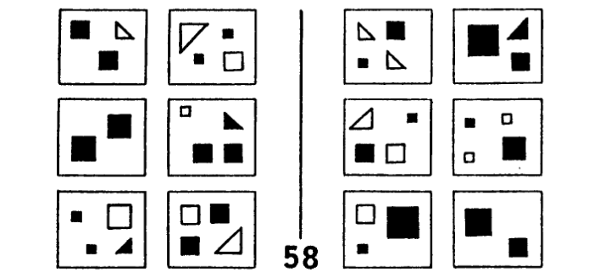
FIGURA 128. Problema de Bongard 58. [Tomado de: M. Bongard, Pattern Recognition.]
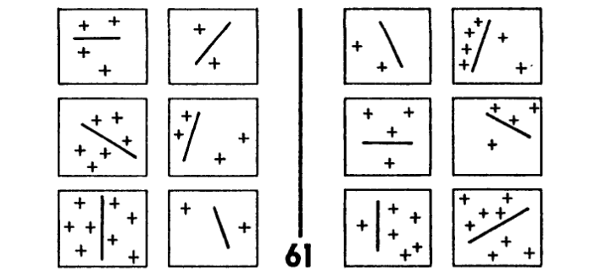
FIGURA 129. Problema de Bongard 61. [Tomado de: M. Bongard, Pattern Recognition.]
El mundo de los problemas de Bongard puede ser considerado un diminuto lugar donde se practica la “ciencia”: es decir, donde el propósito perseguido es el discernimiento de patrones en el mundo. Cuando se buscan patrones, despierta la actividad de hacer, deshacer y rehacer moldes; de deslizar huecos desde un nivel de generalidad a otro; de filtrar y de enfocar. Hay descubrimientos en todos los niveles posibles de complejidad. La teoría de Kuhn en el sentido de que ciertos acontecimientos inusuales, llamados “mutaciones paradigmáticas”, señalan la distinción entre ciencia “normar’ y “revoluciones conceptuales”, por lo visto no es acertada ya que podemos ver la aparición de mutaciones paradigmáticas en toda la extensión del sistema, y en todo momento. La fluidez de las descripciones asegura que las mutaciones paradigmáticas tengan lugar en todas las escalas.
Por supuesto, algunos descubrimientos son más “revolucionarios” que otros, porque tienen efectos más amplios. Por ejemplo, uno puede hacer el descubrimiento de que los problemas 70 y 71 (figura 130) son “el mismo problema”, si los analiza en un nivel suficientemente abstracto. La observación clave es que ambos involucran una autoinclusión de profundidad 2 versus profundidad 1. Éste es un nuevo nivel de descubrimiento con respecto a los problemas de Bongard. Hay un nivel aún más alto, vinculado a la colección entendida como un conjunto; si alguien no ha visto nunca la colección, constituiría un estupendo acertijo, precisamente, pedirle que resuelva cuál es ese nivel. Alcanzar tal resolución sería una penetración revolucionaria, pero es necesario señalar que los mecanismos del pensamiento aptos para lograr ese descubrimiento no son diferentes de los requeridos para desarrollar la solución de un problema individual de Bongard.
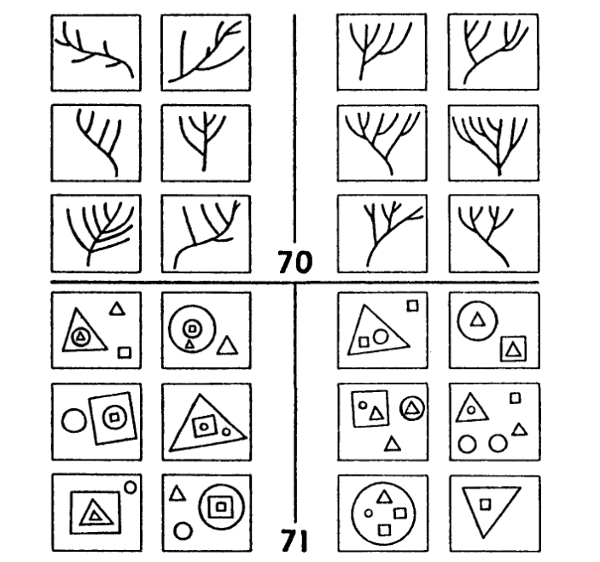
FIGURA 130. Problema de Bongard 70-71. [Tomado de: M. Bongard, Pattern Recognition.]
Por la misma razón, la ciencia real no divide entre períodos “normales” y “revoluciones conceptuales”; por el contrario, las mutaciones paradigmáticas se encuentran por doquier: las hay de mayor y menor dimensión, y en diferentes niveles. La organización recursiva de INT y del diseño G (figuras 32 y 34) suministra un modelo geométrico de esta idea: tienen la misma estructura, llena de saltos discontinuos en todos los niveles, no sólo en el superior, con la única salvedad de que cuanto más bajo es el nivel, más pequeños son los saltos.
Para situar en contexto, en lo posible, todo este programa, permítaseme intentar el señalamiento de dos modos a través de los cuales está relacionado con otros aspectos de la cognoscitividad: no solamente depende de esos otros aspectos, sino que éstos a su vez dependen de él. Me voy a referir primero a la manera en que depende de dichos aspectos. La intuición requerida para saber cuándo omitir distinciones, emprender redescripciones, volver sobre lo andado, cambiar de nivel, etc. es algo que quizá se obtiene sólo después de una larga experiencia de ejercitación del pensamiento en general. Sería muy difícil definir heurísticas para aplicar a estos aspectos sustanciales del programa. En ocasiones, la experiencia personal con relación a objetos reales del mundo tiene un efecto sutil sobre la forma en que se describan o redescriban las cajas. Por ejemplo, ¿quién puede determinar cuál es el grado de familiaridad con los árboles reales que puede ayudar a resolver el PB 70? No es nada probable que, en los seres humanos, la subred de conceptos que tienen pertinencia con respecto a estos problemas pueda ser separada con facilidad de la red total. En cambio, sí es sumamente verosímil que las intuiciones elaboradas a partir de la visión y la manipulación de objetos reales —peines, trenes, encadenamientos, bloques, letras, fajas elásticas, etc.— jueguen un papel orientador invisible, pero importante, en la solución de estos acertijos.
A la inversa, es indudable que la comprensión de situaciones propias del mundo real depende en gran parte de la imaginación visual y de la intuición espacial; por lo tanto, contar con una forma poderosa y flexible de representar patrones del tipo de los de Bongard no puede sino contribuir a la eficacia general de los procesos del pensamiento.
Creo que los problemas de Bongard han sido preparados con mucho detenimiento y que están dotados de una cualidad universal, en el sentido de que a cada uno de ellos corresponde una respuesta correcta única. Es claro que esto puede discutirse, diciendo que la calificación de “correcto” depende profundamente de nuestro carácter de seres humanos, y que las criaturas de otros sistemas estelares pueden disentir totalmente al respecto. A falta de evidencias concretas acerca de esta posibilidad, me mantengo en la certidumbre de que los problemas de Bongard están basados en un sentido de la simplicidad que no se limita al ámbito terráqueo de los seres humanos. Mis observaciones iniciales sobre la eventual importancia de conocer objetos tan indiscutiblemente terráqueos como peines, trenes, fajas elásticas, etc., no choca con la idea de que nuestra noción de la simplicidad es universal, pues lo que interesa no es ninguno de esos objetos individuales, sino el hecho de que, reunidos, se extienden a lo largo de un amplio espacio. Y me parece verosímil que cualquier otra civilización tenga, lo mismo que nosotros, un vasto repertorio de artefactos y de objetos naturales y de experiencias a partir de los cuales efectuar deducciones. En consecuencia, creo que la capacidad de resolver problemas de Bongard se asienta en un sitio muy próximo al núcleo de la inteligencia “pura”, si es que existe tal cosa. Tenemos aquí, entonces, un excelente punto de partida si lo que se quiere es investigar la facultad de descubrir el “significado intrínseco” de patrones o de mensajes. Lamentablemente, sólo hemos reproducido una selección reducida de este incitante conjunto. Confío en que muchos lectores tomarán conocimiento de la colección completa, publicada en la obra que incluimos en la bibliografía.
Los que siguen son algunos de los problemas de reconocimiento de patrones visuales que, aparentemente, los seres humanos hemos “asimilado” por completo en el interior de nuestro inconsciente; son muy llamativos; veamos:
Uno de los medios propuestos para enfrentar las complejidades del reconocimiento de patrones y otros desafíos planteados a los programas IA es la formalización llamada “actor”, obra de Carl Hewitt (similar al lenguaje “Smalltalk” [charla insustancial], desarrollado por Alan Kay y otros), consistente en un programa formulado como colección de actores en interacción, los cuales pueden hacer circular entre sí elaborados mensajes, en todas direcciones. En cierto modo, se asemeja a un grupo heterárquico de procedimientos que se convocan entre sí; la diferencia principal reside en que, mientras los procedimientos, por lo común, sólo hacen circular de una parte a otra un número bastante reducido de argumentaciones, los mensajes intercambiados por los actores pueden llegar a ser discrecionalmente extensos y complejos.
Los actores dotados de la capacidad de intercambiar mensajes se convierten en algo así como agentes autónomos: en realidad, incluso en algo semejante a computadoras autónomas, donde sus mensajes tienen cierta analogía con los programas. Cada actor tiene su manera peculiar de interpretación de cada mensaje; luego, la significación de un mensaje estará subordinada a la circunstancia de qué actor sea el interceptor del mismo. Esto es así porque el actor contiene un sector de programa que interpreta mensajes; así, puede haber tantos intérpretes como actores. Por cierto, es posible que haya muchos actores con intérpretes idénticos, lo cual, en verdad, puede que signifique una gran ventaja, al modo en que, en la célula, es extraordinariamente importante disponer de una multitud de ribosomas idénticos flotando en todo el citoplasma, cada uno de los cuales habrá de interpretar un mensaje —en este caso, el ARN mensajero— de una y la misma manera.
Es interesante considerar la posibilidad de combinar la noción de marco con la noción de actor. Llamemos símbolo a un marco capacitado para generar e interpretar mensajes complejos:
marco + actor = símbolo
Hemos llegado al punto en que podemos ocuparnos de las formas de instrumentación de aquellos elusivos símbolos activos de los Capítulos XI y XII; de aquí en más, en este capítulo, “símbolo” tendrá ese significado. Entre paréntesis, recomiendo al lector que no se culpe si no percibe de inmediato la manera en que se tiene que efectuar esta síntesis. El algo que no está claro aún, pese a que se trata, ciertamente, de una de las vertientes más fascinantes en IA. Además, no cabe la menor duda de que inclusive la mejor síntesis posible entre estas nociones resultará revestida de un poder mucho menor que el de los símbolos reales de la mente humana. En este sentido, llamar “símbolos” a estas síntesis marco-actor es prematuro, pero manifiesta una actitud optimista frente a las cosas.
Volvamos atrás y veamos algunos problemas relacionados con la circulación de mensajes. ¿Cada mensaje estará dirigido específicamente para que haga blanco en un símbolo determinado, o deberá ser lanzado al gran vacío, así como el ARNm es lanzado al citoplasma, para que busque allí su ribosoma? Si los mensajes tienen destinatario, todo símbolo deberá tener una dirección, y los mensajes que le sean remitidos deberán siempre ser enviados a esa recepción de mensajes, donde éstos se limitarían a permanecer hasta que los recogiera un símbolo que los necesite: sería el equivalente de una lista de correos o poste restante. Tal vez la mejor solución sea permitir que existan ambos tipos de mensajes, además de prever distintos tipos de urgencia: entrega inmediata, primera clase, segunda clase, etc. El sistema postal, en su conjunto, es una rica fuente de ideas para los lenguajes de circulación de mensajes, incluyendo curiosidades tales como sobres estampillados y con la dirección impresa (mensajes cuyos remitentes desean respuesta rápida), paquetes postales (mensajes extremadamente extensos que pueden ser enviados a través de una vía lenta), y así siguiendo. El sistema telefónico aportará nuevas inspiraciones cuando agotemos los paralelos postales.
Otra pródiga fuente de analogías para llevar al campo de la circulación de mensajes —por cierto, para el campo del procesamiento de información en general— la constituye, naturalmente, la célula. Ciertos objetos de la célula son enteramente comparables a los actores: particularmente, las enzimas. Cada sitio activo de la enzima actúa como un filtro que reconoce exclusivamente ciertas clases de sustratos (mensajes). De tal modo, una enzima tiene, en efecto, una “dirección”. La enzima está “programada” (en virtud de su estructura ternaria) para realizar ciertas operaciones con ese “mensaje”, y luego devolverlo al mundo. Así, cuando un mensaje circula de una enzima a otra, a lo largo de un recorrido químico, la cantidad de tareas cumplidas puede ser muy grande. Ya hemos descrito las elaboradas clases de mecanismos de retroalimentación que pueden funcionar en las células (sea por inhibición o por represión). Estos mecanismos muestran que pueden surgir complicados controles de procesos, completamente generados por el tipo de circulación de mensajes que existe en la célula.
Una de las cosas más sorprendentes que presentan las enzimas es la forma en que permanecen ociosas, a la espera de ser desencadenadas por el arribo de un sustrato. Cuando esto se produce, la encima entra súbitamente en acción, tal como una planta insectívora. Este género de programa de “disparo inmediato” ha sido utilizado en IA, bajo el nombre de demonio. Lo importante aquí es la idea de contar con muchas “especies” diferentes de subrutinas desencadenables que permanecen a la espera de que se las dispare. En las células, todas las moléculas compuestas y los organelos son construidos mediante un paso simple tas otro. Algunas de estas nuevas estructuras son también, frecuentemente, enzimas, y participan en la construcción de nuevas enzima, las cuales a su vez participan en la construcción de otros tipos de enzimas, etc. Tales cascadas recursivas de enzimas pueden tener efectos drásticos sobre lo que está haciendo una célula. Uno querría ver el mismo proceso de montaje paso simple tras paso simple actuando en IA, en la construcción de subprogramas provechosos. Por ejemplo, la repetición suelda de tal manera circuitos nuevos en nuestro hardware mental, que los tramos de comportamiento reiterados muchas veces pasan a quedar codificados por debajo del nivel consciente. Sería extraordinariamente útil que hubiese una forma análoga de sintetizar tramos eficaces de código, que efectuasen una secuencia de operaciones similar a la producida cuando se ha aprendido algo en un nivel más alto de “conciencia”. Las cascadas de enzimas pueden servir como modelo de la manera en que se podría concretar una cosa así. (El programa llamado “HACKER”, formulado por Gerald Sussman, sintetiza y depura pequeñas subrutinas, de una forma no muy diferente con respecto a las cascadas de enzimas).
Los detectores de similitud (Desi) que vimos aplicados a la resolución de problemas Bongard podrían ser instrumentos como subprogramas semejantes a enzimas. Lo mismo que una de éstas, un Desi vagaría un tanto al azar, topándose con pequeñas estructuras de datos aquí y allá. Luego de rellenar sus dos “sitios activos” con estructuras de datos idénticas. Desi dirigiría un mensaje a otras partes (actores) del programa. En la medida en que se trate de un programa en serie, no tiene mucho sentido disponer de varías réplicas de un Desi, pero en una cabal computadora en paralelo, la regulación del número de réplicas de un subprograma sería una forma de regular el tiempo de espera previsto para que se cumpla una operación, igual que la regulación del número de réplicas de una enzima, en una célula, regular la velocidad con que es cumplida la función respectiva. Y, si pudiesen ser sintetizados nuevos Desi, ello equivaldría a la infiltración de detectores de patrones en los niveles más bajos de nuestra mente.
Dos interesantes y complementarías ideas relativas a la interacción existente entre los símbolos son las de “fisión” y “fusión”. La fisión es la divergencia gradual de un símbolo nuevo con respecto a un símbolo paterno (esto es, con respecto al símbolo que hizo de molde para que el nuevo símbolo fuese copiado). La fusión es lo que ocurre cuando dos (o más) símbolos ajenos entre sí participan en una “activación conjunta”, transmitiendo mensajes tan estrechamente próximos entre sí que aquéllos terminan por unirse, y la combinación, de ahí en más, puede ser considerada un símbolo individual. La fisión es un proceso relativamente inevitable, pues una vez “frotado” un nuevo símbolo a partir de otro anterior, se convierte en autónomo, y sus interacciones con el mundo exterior quedan reflejadas en su estructura interna particular; es decir, lo que al principio fue una réplica perfecta muy pronto pasa a ser imperfecta y luego, lentamente, se va pareciendo cada vez menos al símbolo del cual fue “frotado”. La fusión es una cosa más sutil; ¿cuándo dos conceptos se convierten realmente en uno solo?, ¿la fusión tiene lugar en algún momento preciso?
Este fenómeno de la activación conjunta abre una caja de Pandora de preguntas. Por ejemplo, ¿en qué medida reparamos separadamente en “rasca” y en “cielos” cuando decimos “rascacielos”? Un alemán que recuerda sus guantes (“Handschuhe”), ¿piensa en “zapatos-para-mano”, o no? ¿Y qué pasa con un chino, cuyos carácteres “dōng-xī” (東西, “Este-Oeste”) significan “cosa”? Se trata de un asunto de cierto interés político, además, pues mucha gente sostiene que palabras como “ministro” están fuertemente cargadas de resonancias masculinas. El grado en que las partes se individualicen en el interior del conjunto varía, probablemente, de persona a persona y según las circunstancias.
El problema real que presenta esta noción de “fusión” de símbolos es que resulta muy difícil imaginar algoritmos generales que creen nuevos símbolos significativos a partir de símbolos que se topan. Es como dos cadenas de ADN que se reuniesen; ¿cómo tomar porciones de cada una y recombinarlas en una nueva cadena de ADN, significativa y viable, que codifique un individuo de la misma especie?, ¿o una nueva especie? Las posibilidades de que una combinación azarosa de secciones de ADN codifique alguna cosa que sobreviva son infinitesimales, lo mismo que las posibilidades de que una combinación azarosa de palabras tomadas de dos libros produzca otro libro. Las posibilidades de que la recombinación de ADN tenga sentido en cualquier nivel, fuera del inferior, son pequeñísimas, precisamente porque hay muchos niveles de significación en el ADN; y lo mismo vale para los “símbolos recombinados”.
Creo que mi diálogo Canon Cangrejo es un ejemplo prototípico donde dos ideas chocaron entre sí en mi mente, se conectaron de una nueva forma, y súbitamente adquirió vida en mi mente una nueva clase de estructura verbal. Por supuesto, puedo seguir pensando por separado en cánones cangrejo y en diálogos verbales; ambos siguen siendo activables en forma independiente. Con todo, el símbolo de los diálogos cangrejo-canónicos, obtenidos por fusión, tiene por su parte sus propios modos característicos de activación. A fin de ilustrar esta noción de fusión o “recombinación simbólica” con cierto detalle, querría pues utilizar el desarrollo de mi Canon Cangrejo como un estudio de caso porque, por supuesto, me es muy familiar, y también porque es atractivo, inclusive ejemplificador de cuán lejos puede ser impulsada una idea individual. Mi comentario se dividirá en etapas que siguen las de la meiosis, que es el nombre de la división celular en la cual tiene lugar el “entrecruzamiento“, o recombinación, genética: la fuente de la diversidad, en la evolución.
PROFASE: Comencé con una idea bastante simple, la de que una composición musical, digamos un canon, puede ser imitada verbalmente. Esto se derivó de la observación de que una composición textual y una composición musical pueden ser vinculadas, gracias a que comparten una forma abstracta. El paso siguiente abarcó el intento de concretar parte del potencial de esta vaga aproximación; aquí me topé con la idea de que las “voces” de los cánones pueden ser puestas en correspondencia con los “personajes” de los diálogos: un descubrimiento un tanto obvio, todavía.
Luego, me concentré en tipos específicos de cánones, y recordé que en la Ofrenda Musical había un canon cangrejo. Por esa época, yo había comenzado a escribir diálogos, y tenía solamente dos personajes: Aquiles y la Tortuga. Como el canon cangrejo de Bach tiene dos voces, la correspondencia era perfecta: Aquiles sería una voz, la Tortuga la otra, y uno de ambos haría hacia adelante lo que el otro haría hacia atrás. Pero aquí se me planteaba un problema: ¿en qué nivel debía tener lugar la inversión?, ¿el de la letra?, ¿el de la palabra?, ¿el de la oración? Después de pensarlo, llegué a la conclusión de que el nivel del “discurso dramático” sería el más adecuado.
Ahora que el “esqueleto” de canon cangrejo de Bach ya había sido trasplantado a una forma verbal, cuando menos en proyecto, restaba solamente un problema: cuando las dos voces se cruzaran en el centro, habría un breve período de insistente repetición: un defecto gigantesco. ¿Qué hacer? En este punto, sucedió una cosa curiosa, un cruce de niveles, típico de los actos creativos: la palabra “cangrejo” de la expresión “canon cangrejo” fulguró en mi mente, sin duda a causa de alguna cualidad abstracta compartida por la noción de “tortuga”, e inmediatamente comprendí que, en el centro exacto, yo podía impedir el efecto repetitivo mediante la inclusión de un parlamento especial, a cargo de un nuevo personaje: ¡un Cangrejo! De este modo fue concebido el Cangrejo en la “profase” del Canon Cangrejo: en el entrecruzamiento de Aquiles y la Tortuga (véase figura 131).
FIGURA 131. Un diagrama esquemático del Diálogo Canon Cangrejo.
METAFASE: Tal era el esqueleto de mi Canon Cangrejo. Ingresé entonces en la segunda etapa —la “metafase”— en la cual tenía que convertir a aquél en un cuerpo: una ardua tarea, por cierto. Hice un sinnúmero de ensayos, practicando maneras de obtener que los pares de parlamentos sucesivos tuvieran sentido cuando fuesen leídos en la otra dirección, y experimentando en la búsqueda de significados duales que me permitiesen formularlas de ese modo (por ejemplo, “En absoluto”). Hubo dos versiones iniciales, ambas interesantes, pero débiles. Dejé de trabajar en el libro durante más de un año, y cuando retomé el Canon Cangrejo tenía algunas ideas nuevas. Una de ellas consistía en mencionar un canon de Bach dentro del Diálogo; pensé primero en citar el “Canon per aumentationem, contrario motu”, de la Ofrenda Musical (Canon Perezoso, como yo lo llamo), pero esto comenzó a parecerme un poco tonto, así que, a regañadientes, decidí que, dentro de mi Canon Cangrejo, yo podía aludir al Canon Cangrejo del propio Bach. En realidad, éste fue un punto de giro sustancial, pero yo lo ignoraba entonces.
Ahora bien, si uno de los personajes iba a mencionar una composición de Bach, ¿no sería un recurso torpe la aparición de la misma cosa en boca del otro personaje, en el lugar correspondiente? Bueno, Escher estaba desempeñando un papel similar al de Bach en mis pensamientos y en mi libro, de modo pues que, ¿no habría una forma de modificar ligeramente la línea a fin de que se refiriese a aquél? Al fin y al cabo, en el arte estricto de los cánones, a veces se renuncia a una imitación perfecta de las notas en beneficio de la elegancia o de la belleza. Ni bien tuve esta idea, se me apareció la pintura Día y Noche (figura 49) en la mente. “¡Por supuesto!”, pensé, “es una suerte de canon cangrejo pictórico que tiene, esencialmente, dos voces complementarias que desarrollan el mismo tema hacia izquierda y derecha, y que armonizan entre sí”. Surgía aquí de nuevo la situación de un mismo “esqueleto conceptual” concretado en dos ámbitos diferentes, la música y la plástica, en este caso. Hice hablar a la Tortuga sobre Bach, entonces, y a Aquiles sobre Escher, en lenguaje paralelo; ciertamente, este leve apartamiento con respecto a la imitación estricta retenía el espíritu de los cánones cangrejo.
En este punto, empecé a advertir que estaba sucediendo algo maravilloso: a saber, ¡que el Diálogo se estaba haciendo autorreferencial, sin que yo me lo hubiese propuesto! Más todavía, se trataba de una autorreferencia indirecta, donde los personajes no hablaban directamente del Diálogo que los contenía, sino, en cambio, de estructuras isomórficas (en cierto plano de abstracción) a aquél. Para volcarlo en los términos que he venido empleando, mi Diálogo compartía ahora un “esqueleto conceptual” con G de Gödel, y en consecuencia podía hacerse corresponder con G en la forma, en alguna medida, en que se lo hizo con el Dogma Central, a fin de crear, en este caso, una “Correspongrejo Central”. Esto me llenó de entusiasmo ya que, desde la nada, había llegado a una unidad estéticamente agradable entre Gödel, Escher y Bach.
ANAFASE: El siguiente paso fue absolutamente sobrecogedor. Hacía años que yo conocía la monografía de Caroline MacGillavry a propósito de los mosaicos de Escher, pero un día, hojeándola, mis ojos fueron atraídos por la Lámina 23 (figura 42), pues la vi de una manera enteramente nueva: ¡había allí un auténtico canon cangrejo: la figura del cangrejo estaba manifestada tanto por la forma como por el contenido! Escher, por su parte, no atribuyó ningún título a esta imagen, y es probable que esa coincidencia entre forma y contenido fuese algo que sólo yo advertí, ya que aquél había pintado mosaicos similares, utilizando muchas otras formas animales. No obstante, por casualidad o no, esta lámina sin título era una versión en miniatura de una de las ideas principales de mi libro: la unificación de forma y contenido. Por consiguiente, lleno de deleite bauticé Canon Cangrejo a la imagen, la puse en lugar de Día y Noche, e hice las modificaciones necesarias en los parlamentos de Aquiles y la Tortuga.
Y esto no fue todo. Me había apasionado con la biología molecular: un día en que estaba examinando el libro de Watson en la librería, vi en el índice la palabra “palíndroma”. Al averiguar de qué se trataba, descubrí algo mágico: las estructuras cangrejo-canónicas del ADN; rápidamente, pues, modifiqué con arreglo a ello las palabras del Cangrejo, para que incluyeran un breve comentario acerca de la influencia, debida a sus genes, sobre su inclinación a confundir el desplazamiento hacia adelante con el desplazamiento hacia atrás.
TELOFASE: El último paso tuvo lugar meses más tarde; estaba yo hablando de la ilustración que muestra el segmento cangrejo canónico de ADN (figura 43), cuando reparé en que la ‘A’, la ‘T’ y la ‘C’ de adenina, timina y citosina coincidían —mirabile dictu— con la ‘A’ , la ‘T’ y la ‘C’ de Aquiles, Tortuga y Cangrejo; además, tal como se aparean la adenina y la timina en el ADN, así lo hacen Aquiles y la Tortuga en el Diálogo. Reflexioné un momento y, en otro de esos entrecruzamientos de niveles, vi que ‘G’, la letra apareada con la ‘C’, en el ADN, podía representar a “Gen”. Una vez más, retrocedí de un salto en el interior del Diálogo y practiqué una pequeña cirugía en el parlamento del Cangrejo con el objeto de reflejar este nuevo descubrimiento: ahora, yo tenía una correspondencia entre la estructura del ADN y la estructura del Diálogo. En este sentido, se puede decir que el ADN es un genotipo que codifica un fenotipo: la estructura del Diálogo. Este toque final realza dramáticamente la autorreferencia, y otorga al Diálogo una densidad de significación que yo no había previsto.
Lo anterior sintetiza en forma aproximada la epigénesis del Canon Cangrejo. El proceso en su conjunto puede ser visto como una sucesión de correspondencias entre ideas, en niveles variables de abstracción. Esto es lo que llamo correspondencia conceptual, y los esqueletos conceptuales son las estructuras abstractas que conectan dos ideas diferentes. Así, un esqueleto conceptual es el de la noción abstracta de canon cangrejo:
una estructura que tiene dos partes, las cuales hacen la misma cosa, sólo que avanzando en direcciones opuestas.
Ésta es una imagen geométrica concreta que puede ser manipulada por la mente casi como si fuese un patrón Bongard. En realidad, cuando examino, ahora, el Canon Cangrejo, lo visualizo como dos cadenas que se cruzan en el centro, sitio en el que son unidas mediante un “nudo” (el parlamento de Cangrejo). Esta imagen es tan vívidamente gráfica que se corresponde, en mi mente, con la representación de dos cromosomas homólogos reunidos en su centro por un centrómero, representación extraída directamente de la meiosis, tal como se ve en la figura 132.
FIGURA 132.
En verdad, esta misma imagen fue lo que me inspiró para moldear la descripción de la evolución del Canon Cangrejo siguiendo las etapas de la meiosis, la cual es ciertamente, por su parte, otro ejemplo de correspondencia conceptual.
Hay una diversidad de técnicas para la fusión de los símbolos. Una de ellas consiste en el alineamiento de una idea junto a la otra (¡como si las ideas fuesen lineales!), seguido por la sensata elección de distintas porciones de ambas, y por último la recombinación de dichas porciones en un nuevo símbolo. Esto nos hace recordar de inmediato la recombinación genética. Bien, ¿qué intercambian los cromosomas, y cómo lo hacen? Intercambian genes. ¿Qué elemento es comparable a un gen, en un símbolo? Si los símbolos tienen huecos semejantes a marcos, quizá la respuesta sea: los huecos; pero, ¿cuáles huecos habrá que intercambiar, y por qué? Es aquí donde la fusión cangrejo canónica puede aportar algunas sugerencias. Hacer entrar en correspondencia la noción de “canon cangrejo musical” con la de “diálogo” implicó varias correspondencias auxiliares; en realidad, la primera correspondencia indujo las segundas. Es decir, una vez resuelto que aquellas dos nociones iban a ser fusionadas, el asunto pasó a consistir en observarlas en un nivel donde las partes análogas se manifestaran a la vista, en ir luego más adelante y poner en correspondencia esas partes, y así siguiendo, recursivamente, en todos los niveles donde se manifestaron como huecos en correspondencia cuando “canon cangrejo” y “diálogo” fueron considerados en forma abstracta. ¿De dónde surge, empero, esta perspectiva abstracta? Aquí tocamos la esencia del problema de la correspondencia: ¿de dónde provienen las perspectivas abstractas?, ¿cómo se hace para elaborar una visión abstracta de una noción específica?
Lo que yo denomino esqueleto conceptual es una perspectiva abstraída de un concepto, siguiendo determinada dimensión. En efecto, me he ocupado extensamente de esqueletos conceptuales, en todo el libro, aunque por lo común sin esa denominación. Por ejemplo, muchas de las ideas relativas a los problemas de Bongard pueden ser reformuladas empleando esta terminología. Siempre es de interés, y también, tal vez, de importancia, el hecho de descubrir que dos o más ideas comparten un mismo esqueleto conceptual. Una muestra la tenemos en el fantástico conjunto de conceptos mencionados al comienzo del Contrafactus: un Bicíclope, un uniciclo tándem, un sube-y-sube, el partido de ping-ping, un empate en el primer lugar consigo mismo, una cinta de Möbius de dos lados, los “mellizos Bach”, un concierto de piano para dos manos izquierdas, una fuga a una voz, el acto de aplaudir con una mano, un fonógrafo monoaural de dos canales, un par de extremos izquierdos. Todas estas ideas son “isomórficas” porque comparten este esqueleto conceptual:
una cosa plural convertida en singular y repluralizada erróneamente.
Otras dos ideas de este libro que comparten ese esqueleto conceptual son, (1) la solución de la Tortuga al acertijo planteado por Aquiles, consistente en hallar un substantivo que comenzara y terminara con “LA” (la respuesta de la Tortuga según la cual el “LA”, que yuxtapone dos apariciones en una, cumple esas condiciones), y (2) la demostración Pappus-Gelernter del Teorema Pons Asinorum, donde un triángulo es percibido en segunda instancia como dos. Dicho al margen, estas graciosas mixturas deberían ser apodadas “medios pares”.
Un esqueleto conceptual es como un conjunto de rasgos constantes (por oposición a parámetros y variables), los cuales no habrán de experimentar desplazamientos al tener lugar una repetición subjuntiva o una operación de proyección de correspondencias. La carencia de parámetros o variables propias que permitan diversificaciones puede constituir el núcleo invariante de varias ideas diferentes. Cada caso distinto, tal como “uniciclo tándem”, tiene capas de variabilidad y entonces puede ser “desplazado” de diversas maneras.
Pese a que la denominación “esqueleto conceptual” resuena como absoluta y rígida, la amplitud de su juego es grande. Hay esqueletos conceptuales en diferentes niveles de abstracción. Por ejemplo, el “isomorfismo” entre los problemas Bongard 70 y 71, ya señalado, involucra un esqueleto conceptual de nivel más elevado que el requerido en la resolución de cualquiera de ambos problemas por separado.
Dijimos que los esqueletos conceptuales se presentan en diferentes niveles de abstracción; no sólo eso, sino que, además, su presencia debe extenderse a lo largo de diferentes dimensiones conceptuales. Tomemos como ejemplo la siguiente oración.
“El Vicepresidente es la llanta de refacción del automóvil del gobierno”.
¿Cómo entendemos lo que quiere decir? (Dejando a un lado el aspecto humorístico, que por supuesto comporta una faceta vital). Si se hubiera dicho: “Vea a nuestro gobierno como un automóvil”, sin ninguna explicación previa, uno puede hallar una gran cantidad de correspondencias: volante = presidente, etc., ¿cuáles son los frenos y los amortiguadores?, ¿quién llena el papel de cinturón de seguridad? Como las dos cosas puestas en correspondencia son tan diferentes, es casi inevitable que la correspondencia abarque aspectos funcionales. En consecuencia, uno extraerá, del interior de su almacén de esqueletos conceptuales representativos de partes de automóviles, únicamente aquéllos vinculados a funciones, y no a, digamos, formas. Además, es conveniente situarse en un nivel bastante alto de abstracción, donde la “función” no esté relacionada con contextos demasiado próximos. Supongamos las dos definiciones que siguen de la función de una llanta de refacción: (1) “sustituir una llanta desinflada”, y (2) “sustituir cierta parte inutilizada de un automóvil”; sin duda, es preferible la segunda. Esto responde simplemente al hecho de que un automóvil y un gobierno son tan diferentes que tienen que ser puestos en correspondencia en un alto nivel de abstracción.
Ahora bien, cuando es examinada la oración del ejemplo, hay un ángulo desde el cual la correspondencia parece forzada: de ningún modo, empero, se trata por ello de un procedimiento torpe. En realidad, uno ya tiene un esqueleto conceptual, junto a muchos otros, de la función vicepresidencial, el cual reza: “sustituir cierta parte inutilizada de un gobierno”. En consecuencia, la correspondencia forzada funciona sin dificultad. Supongamos, sin embargo, por el gusto de establecer contrastes, que uno ha extraído otro esqueleto conceptual de “llanta de refacción”, que describe, pongamos por caso, los aspectos físicos de la misma. Entre otras cosas, este esqueleto puede decir que una llanta de refacción es “redonda e inflada”. Está claro que éste no es el modo correcto de proceder. (¿O sí? Como observaba un amigo mío, algunos vicepresidentes tienen bastantes redondeces, ¡y casi todos ellos han sido notablemente inflados!).
Una de las principales características de cada estilo peculiar de pensamiento es la manera en que son clasificadas, y acumuladas en la memoria, las nuevas experiencias, pues ello define cuáles serán las “agarraderas” utilizadas más adelante para recuperarlas. Existe una amplia variedad de “agarraderas” para los acontecimientos, los objetos, las ideas, etc.: para todo lo que puede ser pensado. Esto me vuelve a llamar la atención cada vez que extiendo la mano para encender la radio de mi automóvil y descubro, para mi consternación, ¡que ya estaba encendido! Lo sucedido es que han sido utilizadas dos representaciones independientes de radio. Una es la de “productor de música”, la otra, de “mitigador de aburrimiento”. Yo estoy enterado de que suena música, pero de cualquier manera estoy aburrido; antes de que ambas manifestaciones tengan oportunidad de interactuar, ya ha sido disparado mi reflejo de extender la mano. Reflejo que también se produjo un día, mientras manejaba mi automóvil y deseaba escuchar música, luego de haber dejado la radio en un taller de reparaciones: extraña cosa.
Existen muchas otras representaciones del mismo objeto, tales como:
Todas pueden actuar como puertas de acceso. Pese a que todas están incorporadas a mi símbolo particular de la radio de mi automóvil, el acceso a este símbolo a través de una de estas representaciones no da ingreso al resto de las mismas. Así, es improbable que, cuando extiendo la mano y lo enciendo, ello me inspire para recordarme a mí mismo echado de espaldas para colocar la radio; a la inversa, cuando estoy echado de espaldas haciendo girar tornillos, no es probable que piense en la oportunidad en que escuché el Arte de la Fuga mediante la radio que estoy colocando. Hay “divisiones” entre estos aspectos de mi símbolo, las cuales evitan que mis pensamientos se extiendan ilimitadamente, a la manera de las asociaciones libres. Mis divisiones mentales son importantes porque contienen y canalizan el flujo de mis pensamientos.
Un caso donde estas divisiones son completamente rígidas es el del tabicamiento de palabras de distintos idiomas que se refieren a la misma cosa. Si las divisiones no fuesen tan vigorosas, una persona bilingüe oscilaría constantemente entre el uso de uno y otro idioma, lo cual no le resultaría nada cómodo. Por cierto, los adultos que aprenden dos lenguas nuevas a la vez suelen recaer en tales confusiones, pues las divisiones entre ambas son endebles, y pueden derrumbarse. Es particularmente interesante el caso de los intérpretes, quienes pueden expresarse en cualquiera de las lenguas que dominan, como si las divisiones entre éstas fuesen inexpugnables y, sin embargo, a voluntad, pueden derribarlas para permitir el acceso a una lengua desde otra, lo cual hace posible la traducción. Steiner, cuya educación fue trilingüe, dedica algunas páginas de After Babel al entremezclamiento de francés, inglés y alemán en los estratos de su mente, y al modo en que el dominio de diferentes idiomas proporciona diferentes puertas de ingreso a los conceptos.
Cuando se ve que dos ideas, en cierto nivel de abstracción, comparten esqueletos conceptuales, pueden suceder diversas cosas. Generalmente, la primera consiste en un acercamiento tipo zoom a ambas ideas y, empleando como guía la equiparación de nivel más alto, se trata de identificar las subideas en correspondencia. En ocasiones, la equiparación puede ser llevada varios niveles hacia abajo, lo que manifestaría un isomorfismo profundo. Otras veces, este movimiento se detiene antes, y lo que revela es una analogía o similitud. Hay veces, además, en que la similitud de alto nivel es tan compulsiva que, aun cuando aparentemente no haya continuación de la correspondencia en el nivel inferior, se sigue adelante y se la elabora: esto es una equiparación forzada.
Tenemos muestras de equiparación forzada cotidianamente, en las caricaturas de tema político que aparecen en los periódicos: una figura política es retratada como un avión, un buque, un pez, o como la Mona Lisa; un gobierno es un ser humano, un pájaro, un barril de petróleo; un tratado es una cartera de documentos, una espada o un tarro con lombrices; y así siguiendo indefinidamente. Lo fascinante es la facilidad con que entendemos la correspondencia sugerida y en la exacta medida de la profundidad prevista: no llevamos la correspondencia a una profundidad mayor ni tampoco la detenemos demasiado cerca de la superficie.
Otro ejemplo de forzamiento de una cosa a ajustarse al molde de otra lo tenemos en mi decisión de describir el desarrollo de mi Canon Cangrejo mediante la utilización de los términos de la meiosis. A tal decisión llegué por etapas; primero, advertí la existencia de un esqueleto conceptual común entre el Canon Cangrejo y la imagen de los cromosomas reunidos por un centrómero; esto me suministró la inspiración del equiparamiento forzado. Luego, vi que una semejanza de alto nivel abarcaba “crecimiento”, “estadios” y “recombinación”; entonces, sencillamente impulsé la analogía con la mayor energía que me fue posible; la tentatividad —igual que en la resolución de los problemas de Bongard— llenó aquí una función muy importante: me moví hacia adelante y hacia atrás antes de descubrir una equiparación que me dejara satisfecho.
Un tercer ejemplo de correspondencia conceptual es provisto por el Correspondogma Central. Inicialmente, advertí una similitud de alto nivel entre los descubrimientos de los lógicos matemáticos y los de los biólogos moleculares; luego, la extendí a los niveles inferiores hasta que encontré una fuerte analogía. Para reforzarla aún más, elegí una numeración Gödel que imitase el Código Genético. Éste fue el único elemento de equiparación forzada en el Correspondogma Central.
Equiparaciones forzadas, analogías y metáforas no pueden ser fácilmente deslindadas entre sí. Los relatores deportivos usan a menudo vívidas imágenes que son muy difíciles de encasillar. Por ejemplo, en una metáfora como “El Barcelona [refiriéndose al equipo de fútbol] está haciendo girar sus ruedas”, es arduo establecer con exactitud qué representación despierta: ¿adjudicamos las ruedas al equipo en su conjunto?, ¿o a cada uno de los jugadores? Probablemente, ni una ni otra cosa, sino que, durante un breve instante, nos asaltará la imagen de ruedas que giran sobre el fango o sobre la nieve y luego, de cierta misteriosa manera, serán seleccionadas sólo las partes pertinentes, y transferidas a la actuación del equipo. ¿Cuán profundamente son proyectados entre sí el equipo de fútbol y el automóvil, durante aquel breve segundo inicial?
Trataré de reunir los cabos sueltos: he presentado un buen número de ideas vinculadas con la creación, maniquilación y comparación de símbolos. La mayoría de aquéllas están ligadas, de alguna manera, al deslizamiento, bajo el supuesto de que los conceptos están formados por algunos elementos fuertemente arraigados, y también por elementos carentes de una adhesión tan firme, elementos que provienen de diferentes niveles de los contextos autoincluidos (marcos). Los elementos de la segunda clase pueden ser desalojados y sustituidos bastante fácilmente, lo cual, según las circunstancias, puede originar una “repetición instantánea subjuntiva”, una equiparación forzada o una analogía. Un proceso donde, dados dos símbolos, algunas partes de cada uno de éstos son desalojadas, mientras que otras son conservadas, puede dar lugar a un fusión de los dos símbolos citados.
Resulta obvio que estamos hablando de la mecanización de la creatividad. ¿Y esto no configura una contradicción en los términos? Pareciera, pero realmente no es así. La creatividad es la esencia de todo aquello que no es mecánico. Sin embargo, todo acto creativo es mecánico: tiene su explicación, lo mismo que la tiene un caso de hipo, ni más ni menos. El sustrato mecánico de la creatividad puede ocultarse a la vista, pero existe. A la inversa, hay algo no mecánico en los programas flexibles, inclusive en la actualidad. Puede que ello no sea equivalente a la creatividad, pero cuando los programas dejan de ser transparentes para sus creadores, es que ha comenzado la marcha de acercamiento a la creatividad.
Es una noción generalizada la de que la arbitrariedad es un ingrediente indispensable de los actos creativos. Esto puede ser cierto, pero no tiene ninguna relación con la mecanizabilidad —o, mejor, ¡la programabilidad!— de la creatividad. El mundo es una acumulación gigantesca de arbitrariedades; cuando reflejamos dentro nuestro una parte del mundo, absorbemos algo de esa arbitrariedad. Los patrones desencadenantes de símbolos, en consecuencia, pueden conducirnos por recorridos de la más extrema apariencia arbitraria, simplemente porque son producto de nuestras interacciones con un mundo loco y arbitrario. Y esto también puede darse en un programa de computadora. La arbitrariedad es un rasgo intrínseco del pensamiento, no algo que tiene que ser “inseminado artificialmente” a través de tiradas de dados, o bien de núcleos en desintegración, o de tablas numéricas caprichosas, o lo que a uno se le ocurra. Es un insulto a la creatividad humana suponer que descansa en recursos azarosos de tal tipo.
Lo que vemos como arbitrariedad es, comúnmente, nada más que una consecuencia de la observación de algo simétrico a través de un filtro “oblicuo”. Un elegante ejemplo es el aportado por las dos maneras de Salviati de analizar el número π/4. Pese a que la expansión decimal de π/4 no es literalmente arbitraria, sí lo es en la medida en que ello es necesario para el cumplimiento de muchos objetivos: es “seudoarbitraria”. La matemática está llena de seudoarbitrariedades: las suficientes como para proveer a todos los creadores posibles de toda época.
Así como en la ciencia las “revoluciones conceptuales” invaden todos sus niveles en todos los momentos, el pensamiento de los individuos es atravesado una y otra vez por los actos creativos. Éstos no tienen lugar solamente en el plano más elevado: se producen en cualquier sitio; la mayor parte de los mismos tiene dimensiones pequeñas y ha sido ejecutada un millón de ocasiones con anterioridad, pero estos actos son parientes muy cercanos de los actos más nuevos y altamente creativos. Los programas de computadora de la actualidad, empero, no parecen producir muchas creaciones pequeñas; la mayor parte de su tarea sigue siendo “mecánica”. Esto sólo prueba que no están listos para simular el modo en que pensamos, sino que se están aproximando a ello.
Quizá la diferencia entre las ideas altamente creativas y las comunes radique en alguna motivación que combine belleza, simplicidad y armonía. En realidad, tengo predilección al respecto por una “meta-analogía” que se me ocurrió, basada en la comparación entre analogías y acordes. El esquema es simple: las ideas superficialmente vinculadas, por lo común, no lo están a una mayor profundidad; a la vez, las ideas profundamente vinculadas por lo común muestran disparidad en los planos de superficie. La analogía con los acordes surge con naturalidad: las notas físicamente contiguas son armónicamente distantes (por ejemplo, E-F-G [mi, fa, sol]); y las notas armónicamente contiguas son físicamente distantes (por ejemplo, G-E-B [sol, mi, si]). Las ideas que comparten un esqueleto conceptual guardan una cierta analogía con la armonía; estas armónicas “ideas-acordes” están a menudo muy separadas, como si estuviesen dispuestas en un imaginario “teclado de conceptos”. Por cierto, no basta con cubrir la distancia separatoria ejecutando alguna pulsación conocida: ¡puede salir un acorde de séptima o de novena! Tal vez la presente analogía sea como un acorde de novena… amplio pero disonante.
Los problemas de Bongard fueron elegidos como eje de este capítulo porque, cuando se los estudia, se entiende que el elusivo sentido de los patrones que los seres humanos heredamos de nuestros genes abarca todos los mecanismos de representación del conocimiento, lo cual incluye los contextos autoincluidos, los esqueletos y correspondencias conceptuales, la deslizabilidad, las descripciones y metadescripciones y sus interacciones, la fisión y fusión de símbolos, las representaciones múltiples (ajustadas a diferentes dimensiones y a diferentes niveles de abstracción), expectativas subsidiarias, y todo lo demás.
En la actualidad, se puede tener la total certidumbre de que, si un programa consigue localizar patrones en una área, en otra área los pasará por alto, en tanto que para nosotros serán evidentes en ambas por igual. El lector puede recordar que ya aludí a esto en el Capítulo I, cuando dije que las máquinas no son influidas por la repetición, en tanto que las personas sí. Veamos el caso de SHRDLU. Si Eta Oin teclea la oración “Toma un bloque rojo grande y deposítalo”, y repite esta misma orden una y otra vez, SHRDLU la acatará alegremente de la mismísima manera una y otra vez, exactamente así como una máquina de sumar imprime “4” una y otra vez, si un humano tiene la santa paciencia de teclear “2 + 2” una y otra vez. Los seres humanos no proceden así: si un patrón aparece una y otra vez, lo identifican. SHRDLU no fue construido con el potencial necesario para formar nuevos conceptos o para reconocer patrones; no tiene el sentido de la visión panorámica, aun si se lo pone a prueba al respecto una y otra vez.
La capacidad del manejo de SHRDLU es inmensamente flexible, dentro de ciertos límites. SHRDLU puede comprender oraciones de gran complejidad sintáctica, o que contengan ambigüedades semánticas, en la medida en que puedan ser resueltas mediante el examen de la base de datos, pero no puede manejar un lenguaje “confuso”. Por ejemplo, consideremos la oración: “¿Cuántos bloques van uno encima del otro para formar una torre?”. Nosotros la comprendemos de inmediato, pero carece de sentido si es interpretada literalmente, pese a que no se ha utilizado ninguna expresión idiomática. “Van uno encima del otro” es una expresión imprecisa que, no obstante, logra que un ser humano capte perfectamente la imagen prevista. Son muy pocas las personas que puedan ser inducidas, en este caso, a visualizar una paradójica disposición con dos bloques, cada uno de los cuales está encima del otro, o a imaginar bloques que estén “yendo” a alguna parte.
Lo sorprendente del lenguaje es la imprecisión con que lo manejamos y cómo, pese a ello, nos es posible servirnos satisfactoriamente de él. SHRDLU utiliza las palabras de una manera “metálica”; en cambio, las personas lo hacen de una manera “maleable”, “elástica”, e inclusive de “plastilina”. Si las palabras fuesen tuercas y bulones, lo que hace la gente es conseguir que cualquier tuerca se ajuste a cualquier bulón, mediante el simple recurso de comprimir y estrujar uno dentro del otro, tal como en algunas pinturas surrealistas donde todas las cosas presentan una consistencia blanda. El lenguaje, en manos humanas, se transforma prácticamente en un elemento fluido, pese al grano grueso de sus componentes.
Recientemente, la investigación en IA relativa a la comprensión de lenguajes naturales se ha apartado un tanto de la comprensión de oraciones individuales, tomadas separadamente, y se ha acercado a áreas tales como la comprensión de narraciones infantiles simples. Lo que sigue es una conocida muestra festiva de ese género, que ilustra el carácter inconcluso de las situaciones de la vida real:
Un hombre viajaba en un avión.
Infortunadamente, resbaló y se cayó.
Afortunadamente, tenía un paracaídas.
Infortunadamente, no se abrió.
Afortunadamente, debajo de él había una montaña de heno.
Infortunadamente, sobresalía allí una horquilla.
Afortunadamente, el hombre pasó a un lado de la horquilla.
Infortunadamente, pasó al lado de la montaña de heno.
Esto puede ser extendido indefinidamente. La representación de esta sencilla narración dentro de un sistema basado en marcos sería sumamente compleja, y comprendería la activación conjunta de marcos para los conceptos de hombre, avión, resbalar, paracaídas, caída, etc., etc.
Veamos ahora este breve y conmovedor relato:
Margarita sujetaba con fuerza el hilo de su hermoso globo recién comprado. De pronto, una racha de viento se lo arrebató y lo empujó hacia un árbol. El globo chocó con una rama y reventó. Margarita lloraba y lloraba.[4]
Para comprender esta narración, es necesario leer muchas cosas entre líneas. Por ejemplo: Margarita es una niña. El globo es de juguete, con un hilo destinado a que un niño lo sujete. Puede que no sea bello para un adulto, pero sí lo es a los ojos de un niño. Margarita está a la intemperie. El “lo” que el viento le arrebató es el globo. El viento no se llevó a la niña junto con el globo; ella lo soltó. Los globos pueden romperse en contacto con una punta aguda. Una vez que se han roto, no se los puede componer. Los niños pequeños gustan mucho de los globos y llegan a sentirse amargamente decepcionados cuando éstos se rompen. Margarita vio que su globo estaba roto. Los niños lloran cuando están apesadumbrados. “Llorar y llorar” es llorar con fuerza y durante mucho rato. Margarita lloró y lloró a causa de su pesadumbre ante la destrucción de su globo.
Lo anterior probablemente signifique tan sólo una pequeña fracción de lo que está ausente en el nivel de superficie. Un programa debe contar con todo este conocimiento para saber de qué se trata el grupo de enunciados. Se podría objetar que, aun cuando el programa “entienda” lo que se ha dicho, en un sentido intelectivo, jamás lo comprenderá realmente, hasta que no haya llorado y llorado. ¿Y cuándo conseguirá semejante cosa una computadora? Ésta es la clase de planteamiento humanístico al que se aboca Joseph Weizenbaum en su libro Computer Power and Human Reason; pienso, por mi parte, que es un tema importante: en realidad, un tema verdaderamente muy profundo. Por desdicha, muchos investigadores de IA se muestran poco dispuestos, en la actualidad, a considerar seriamente este problema. En alguna medida, con todo, los asiste la razón, pues es un poco prematuro dedicarse ahora al llanto de las computadoras: primero, es necesario ocuparse de las reglas que permitan a las computadoras habérselas con el lenguaje y con otras cosas; en su oportunidad, nos enfrentaremos en cuestiones de mayor profundidad.
Pareciera a veces que hay una ausencia tan completa de reglas que gobiernen el comportamiento, ¡que simplemente los seres humanos no son gobernados por reglas! Pero esto es una ilusión, comparable a la de creer que los cristales y los metales son consecuencia de rígidas leyes subyacentes, pero que no ocurre así con los fluidos o con las flores. Volveremos sobre este punto en el siguiente capítulo.
El proceso mismo de la lógica actuando internamente en la mente puede que tenga mayor analogía con una serie de operaciones a propósito de pinturas simbólicas, una suerte de abstracta analogía del alfabeto chino o de ciertas descripciones mayas de acontecimientos, salvo que los elementos no son meramente palabras sino más bien oraciones o relatos completos, dotados de enlaces entre sí que los constituyen en una suerte de meta o supralógica, con sus reglas propias.[5]
Es difícil para muchos especialistas expresar vívidamente —inclusive, posiblemente, recordar— qué los impulsó originalmente a apasionarse con su disciplina. A la inversa, alguien ajeno puede comprender una de esas pasiones y ser capaz de articularla con precisión. Creo que ésta es la razón por la cual la anterior cita de Ulam me ha atraído, ya que transmite poéticamente la rareza de la empresa que persigue IA y al mismo tiempo muestra fe en la misma. Y uno debe mantenerse con fe en este aspecto, ¡pues hay tanto por andar todavía!
Para concluir este capítulo, quiero presentar diez “Preguntas y Especulaciones” acerca de IA. No seré tan audaz como para hablar de “Respuestas”, pues lo que incluyo son mis opiniones personales, las cuales pueden modificarse en la medida en que yo aprenda más al respecto o en que IA avance en su desarrollo. (En lo que sigue, la expresión “programa IA” significa un programa muy adelantado con respecto a los programas contemporáneos: un programa Inteligente Absoluto. Asimismo, es probable que las palabras “programa” y “computadora” conlleven un exceso de connotaciones mecanicistas, pero nos resignaremos a ellas, de todos modos).
Pregunta: ¿Un programa de computadora compondrá alguna vez música bella?
Especulación: Sí, pero no próximamente. La música es un lenguaje emocional, y antes de que los programas experimenten emociones como las nuestras no habrá manera de conseguir que un programa componga nada dotado de belleza. Puede haber “adulteraciones”, es decir, imitaciones superficiales de la sintaxis de música ya existente, pero, a pesar de lo que se pueda creer a primera vista, en la expresión musical hay mucho más de lo que puede ser capturado por las reglas sintácticas. Falta mucho tiempo para que los programas de computadora compositores de música produzcan nuevos géneros de belleza. Llevaré esta reflexión un poco más allá: pensar —esta sugerencia ha llegado a mis oídos— que pronto podremos ordenar a un modelo de mesa de “caja musical” preprogramada, fabricada en serie y obtenible por veinte dólares mediante envío postal, que haga surgir de sus estériles circuitos composiciones que pudieron haber sido creadas por Chopin o por Bach si hubiesen vivido más tiempo, implica una grotesca y lamentable subestimación de la profundidad del espíritu humano. Para que un programa produzca la música que esos autores produjeron tendría que enfrentar al mundo por sí mismo, afanándose en atravesar el laberinto de la vida y sintiendo cada momento de esa experiencia. Tendría que comprender el gozo y la soledad de una fría noche ventosa, la necesidad de una caricia, la inaccesibilidad de una población distante, el desgarramiento y el consuelo tras la muerte de un ser humano. Tendría que conocer la resignación y el hastío de la vida, el dolor y la desesperación, la determinación y la victoria, la devoción y el temor reverencial. Tendría que haber experimentado la mezcla de elementos opuestos como la esperanza y el miedo, la angustia y el regocijo, la serenidad y la ansiedad. E integrado todo ello como la carne al hueso tendría que tener sentido de la gracia, del humor, del ritmo, y un sentido de lo imprevisto, además, por supuesto, de una exquisita conciencia de la magia de la creación pura. Aquí, y solamente aquí, se encuentran las fuentes de la significación musical.
Pregunta: ¿Las emociones serán explícitamente programadas en una máquina?
Especulación: No. Es una pretensión ridícula. Toda simulación directa de las emociones —PARRY, pongamos por caso— no puede acercarse a la complejidad de la emotividad humana, la cual tiene su origen indirecto en la organización de la mente. Los programas y las máquinas adquirirán emociones de la misma forma: en calidad de subproductos de su estructura, según el modo en que estén organizados, y no gracias a una programación directa. Así, por ejemplo, nadie formulará una subrutina de “enamorarse”, así como nadie formularía una subrutina de “comisión de errores”. “Enamorarse” es una descripción que insertamos en un proceso complejo de un sistema complejo; ¡no tiene aplicación allí un módulo individual, interior al sistema, con la función de ser el único responsable de aquélla!
Pregunta: ¿Una computadora que piense será capaz de sumar con rapidez?
Especulación: Tal vez no. Los seres humanos mismos estamos compuestos de un hardware que realiza refinados cálculos, lo cual no significa que nuestro nivel simbólico, allí donde somos “nosotros”, sepa cómo efectuamos dichos cálculos. Voy a formularlo de esta manera: no hay medios que nos permitan alimentar nuestras neuronas con números, para que nos sumen la cuenta de la tienda de abarrotes. Por suerte, nuestro nivel simbólico (es decir, nosotros) no puede tener acceso a las neuronas que están elaborando nuestro pensamiento: de no ser así, nuestro cerebro se sumiría en confusión. Si parafraseamos nuevamente a Descartes, diríamos:
“Pienso; luego carezco de acceso a los niveles donde sumo”.
¿Por qué esto no puede ser igual en un programa inteligente? No se debe admitir que tenga acceso a los circuitos que están elaborando su pensamiento: de no ser así, la UCP se sumiría en confusión. Hablando seriamente ahora, una máquina que apruebe la verificación Turing puede también, perfectamente, sumar con la misma lentitud que el lector o que yo, y por razones similares. Esa máquina no se limitará a representar el número 2 mediante los dos bits “10”, sino a través de un acabado concepto, tal como nosotros, el cual rebosará de asociaciones tales como la de homonimia, con las secuencias d-o-s de, por ejemplo, cansados o dosis; o con las palabras “pareja” y “ambos”; con una multitud, en fin, de imágenes mentales como los puntos del dominó, la forma del numeral ‘2’, las nociones de alternancia, de paridad, de imparidad, etc., etc… Con todo este “exceso de equipaje” a sus espaldas, un programa inteligente se hará muy perezoso para sumar. Por supuesto, podríamos darle una “minicalculadora”, por decir así (o incorporarle una); sus respuestas serían muy rápidas, pero su desempeño sería semejante al de una persona provista de una calculadora similar. En la máquina, habría dos partes separadas: una, confiable pero ininteligente; otra, inteligente pero falible. Uno no podría dar por seguro que el sistema combinado fuese confiable en una medida mayor que una combinación entre ser humano y máquina. De manera, pues, que si estamos en pos de respuestas correctas, dejemos actuar a la minicalculadora: ¡no pongamos en juego la inteligencia!
Pregunta: ¿Habrá programas de ajedrez que derroten a cualquier oponente?
Especulación: No. Puede haber programas que puedan derrotar a quien sea al ajedrez, pero no exclusivamente a los jugadores de ajedrez. Se tratará de programas dotados de inteligencia general, y serán tan temperamentales como las personas. “¿Jugamos al ajedrez?”. “No, estoy aburrido del ajedrez; hablemos de poesía”: éste puede ser el tipo de diálogo que se sostendría con un programa capaz de derrotar a quien sea, pues la inteligencia real está basada en una capacidad de visión panorámica total —esto es, en la capacidad programada de “brincar fuera del sistema”, por hablar de este modo—, al menos en la medida en que nosotros disponemos de esa facultad. Una vez obtenido ese estado, no podremos circunscribir el programa: éste habrá sobrepasado determinado punto crítico y tendremos que hacer frente a los hechos que hemos suscitado.
Pregunta: ¿Habrá lugares específicos de la memoria que almacenen parámetros encargados de gobernar el comportamiento del programa tales que, si accedemos a ellos y los modificamos, conseguiremos que el programa sea más sagaz o más inepto o más creativo o más interesado en materia de fútbol? En resumen, ¿estaremos en condiciones de “sintonizar” el programa mediante manipulaciones en niveles relativamente bajos?
Especulación: No. El programa no respondería en absoluto a las modificaciones de cualquier elemento particular de la memoria, por lo mismo que nosotros seguimos siendo exactamente los mismos a pesar de que diariamente mueren miles de neuronas en nuestro cerebro (¡!). Si se hurga ansiosamente en el programa, entonces sólo se conseguirá dañarlo, tal como si practicáramos una irresponsable neurocirugía en un ser humano. No existirá ninguna localización “mágica” en la memoria donde, pongamos por caso, esté asentado el cociente intelectual del programa. Otra vez nos encontramos con la situación de que ello será un rasgo que surja como consecuencia del comportamiento del nivel inferior, sin emplazamiento específico en parte alguna. Lo mismo vale para aspectos tales como “el número de ítems que puede retener la memoria a corto plazo del programa”, “en qué grado le gusta la física”, etcétera.
Pregunta: ¿Podría “sintonizarse” un programa IA para que actúe como yo, o para que actúe como usted, o para que actúe como ambos, por partes iguales?
Especulación: No. Un programa inteligente no será más camaleónico de lo que pueden serlo los seres humanos. Se basará en la fidelidad de sus memorias y no podrá revolotear entre personalidades. La idea de modificar parámetros internos para “sintonizar una nueva personalidad” revela una ridícula subestimación de la complejidad de la personalidad.
Pregunta: ¿Habrá un “corazón” en un programa IA, o consistirá simplemente en “bucles sin sentido y en secuencias de operaciones triviales” (según las palabras de Marvin Minsky)?[6]
Especulación: Si pudiéramos dirigir nuestra vista hasta el fondo, como si se tratase de una charca poco profunda, seguramente veríamos nada más que “bucles sin sentido y secuencias de operaciones triviales”, y también seguramente no veríamos ningún corazón”. Pero hay dos puntos de vista extremos en IA: uno dice que la mente humana, por razones esenciales y misteriosas, es improgramable. Según el otro, todo lo que hace falta es sencillamente ensamblar los adecuados “dispositivos heurísticos: optimizadores múltiples, recursos para el reconocimiento de patrones, álgebras planificadoras, procedimientos de tipo recursivo, y así siguiendo”;[7] con esto bastará para obtener inteligencia. Yo me encuentro en algún sitio intermedio entre ambos puntos, pues creo que la “charca” de un programa IA resultará tan profunda y turbia que no podremos escudriñar la distancia entre la superficie y el fondo. Si observamos desde arriba, los bucles serán invisibles, tal como lo son hoy en día, para la mayoría de los programadores, los electrones portadores de corriente. Cuando hayamos creado un programa que apruebe la verificación Turing, veremos un “corazón”, aun sabiendo que no lo hay.
Pregunta: ¿Los programas IA llegarán a ser “superinteligentes” alguna vez?
Especulación: No lo sé. No hay evidencia de que seamos capaces de entender una “superinteligencia”, de encontrar con qué relacionarla y, ni siquiera, de saber si el concepto tiene sentido. Por ejemplo, nuestra inteligencia está vinculada a la velocidad del pensamiento. Si nuestros reflejos hubieran sido diez veces más rápidos o más lentos, habríamos desarrollado un conjunto de conceptos enteramente distinto para describir el mundo. Una criatura cuya visión del mundo sea radicalmente diferente puede carecer de mayores puntos de contacto con nosotros. A menudo me he preguntado si podría haber, digamos, composiciones musicales que sean a Bach lo que Bach es a las tonadas populares: “Bach al cuadrado”, por expresarlo así. ¿Y sería yo capaz de comprenderlas? Es posible que tal música exista en torno mío y que yo no la reconozca, así como los perros no pueden entender la palabra. La idea de superinteligencia es muy extraña. Como quiera que sea, no creo que sea el objetivo de la investigación en IA, aunque si alguna vez se alcanza el nivel de la inteligencia humana, indudablemente el paso subsiguiente será alcanzar el nivel de la superinteligencia: no sólo en lo que respecta a nosotros, sino también para nuestros colegas, los programas de IA, quienes compartirán el mismo interés hacia IA y la superinteligencia, Se comprende que, muy probablemente, los programas de IA tendrán una extraordinaria curiosidad a propósito de IA en general.
Pregunta: Parece usted decir que los programas IA serán virtualmente idénticos a los seres humanos. ¿No habrá ninguna diferencia?
Especulación: Quizá las diferencias entre los programas IA y las personas sean más amplias que las existentes entre la mayoría de los seres humanos. Es casi imposible imaginar que el “cuerpo” donde se albergue un programa IA no lo afecte en forma profunda. De modo que, excepto si residiera en una réplica pasmosamente fiel del cuerpo humano —¿y por qué va a tener que ser así?—, lo más probable es que tenga perspectivas enormemente diferentes sobre qué es importante, interesante, etc. En una oportunidad, Wittgenstein hizo una observación graciosa: “Si un león hablara, no lo entenderíamos”. Esto me hizo pensar en el cuadro de Rousseau con el manso león y la gitana dormida, en el páramo iluminado por la luna. Sin embargo, ¿cómo lo sabe Wittgenstein? Mi sospecha es que todo programa IA, si bien nos será inteligible, tiene que parecernos bastante ajeno. Por eso mismo, nos costará mucho trabajo establecer si estamos ocupándonos de un programa IA, o tan sólo de un programa “misterioso”.
Pregunta: ¿Cuando hayamos elaborado un programa inteligente, comprenderemos qué son la inteligencia, la conciencia, el libre albedrío y el yo?
Especulación: En cierto modo; todo depende de lo que se quiera decir con “comprender”. En un nivel visceral, es probable que cada uno de nosotros tenga la mejor comprensión que puede de todo aquello, en un comienzo. Es algo semejante a escuchar música. ¿Comprendemos a Bach realmente porque lo analizamos? ¿O lo comprendimos en aquel momento en que sentimos que hacía vibrar todos los nervios de nuestro cuerpo? ¿Comprendemos que la velocidad de la luz es constante dentro de todo marco de referencia inerte? Podemos asimilarlo matemáticamente, pero nadie en el mundo tiene una intuición verdaderamente relativista. Y, tal vez, nadie llegue a comprender jamás los misterios de la inteligencia y de la conciencia, a través de un camino intuitivo. Podemos comprender a la gente, y es posible que no podamos llegar más allá de eso.