
FIGURA 113. Alan Turing, después de una carrera exitosa (mayo de 1950). [Tomado de: Sara Turing, Alan M. Turing (Cambridge, U. K.: W. Heffer & Sons, 1959).]
Inteligencia Artificial: mirada retrospectiva

FIGURA 113. Alan Turing, después de una carrera exitosa (mayo de 1950). [Tomado de: Sara Turing, Alan M. Turing (Cambridge, U. K.: W. Heffer & Sons, 1959).]
EN 1950, ALAN TURING escribió un artículo extraordinariamente profético e incitante sobre Inteligencia Artificial. Lo intituló “Computing Machinery and Intelligence”, y apareció en la revista Mind.[1] Haré diversos comentarios acerca de este artículo, pero antes quiero incluir algunos datos sobre la persona de Turing.
Alan Mathison Turing nació en Londres, en 1912; desde niño, se mostró pleno de curiosidad y de agudeza. Muy dotado en matemática, asistió a Cambridge, donde su interés por las máquinas y por la lógica matemática se entrecruzaron fértilmente, lo cual trajo como resultado su célebre trabajo sobre “números computables”, donde inventa la teoría de las máquinas Turing y demuestra el carácter irresoluble del problema de la detención. En la década de los cuarenta, sus preocupaciones se volcaron, desde la teoría de las máquinas computadoras, hacia la construcción concreta de computadoras reales. Fue una de las principales figuras en el desarrollo de las computadoras en Gran Bretaña, y un tenaz defensor de la Inteligencia Artificial, cuando ésta comenzó a ser impugnada. Uno de sus mejores amigos fue David Champernowne (quien, más adelante, trabajó en la composición de música mediante computadoras). Champernowne y Turing fueron entusiastas ajedrecistas; inventaron el ajedrez “vuelta a la casa”: después de mover, el jugador da una vuelta en torno a la casa; si regresa antes que su oponente haya jugado, tiene derecho a mover de nuevo. Ya más seriamente, Turing y Champernowne inventaron el primer programa jugador de ajedrez, el cual recibió el nombre de “Turochamp”. Turing murió joven, a los cuarenta y un años, por razones accidentales, aparentemente vinculadas con el consumo de ciertos productos químicos. Hubo quienes hablaron de suicidio. Su madre, Sara Turing, escribió su biografía; de los testimonios que ella cita, se obtiene la impresión de que Turing no tuvo nada de convencional, y de que en cierto sentido careció completamente de tacto, pero que fue tan honesto y recto que ello lo hizo vulnerable al mundo. Amaba los juegos, el ajedrez, los niños y las carreras de bicicleta; fue un destacado corredor de fondo. En sus épocas de estudiante, en Cambridge, compró un violín de segunda mano y aprendió a tocar por sí mismo; pese a no tener una acendrada vocación musical, disfrutó mucho con esta actividad. Fue un tanto excéntrico, dado a entregar toda su energía a las orientaciones más dispares. Una de las áreas que investigó fue el problema de la morfogénesis en biología. Según su madre, Turing tenía “un particular apego por los Papeles Póstumos del Club Pickwick”, pero “la poesía, salvo la de Shakespeare, no significaba nada para él”. Alan Turing fue un verdadero pionero en el campo de la ciencia de las computadoras.
El artículo de Turing comienza con la frase: “Me propongo considerar la pregunta ¿Las máquinas pueden pensar?”. Puesto que, como él señala, esos términos encierran una petición de principios, es obvio que debemos buscar un modo operacional de enfocar el problema. Dicho modo, sugiere Turing, está contenido en lo que él llama el “juego de la imitación”, conocido actualmente como la verificación Turing. Éste lo presenta de la siguiente manera:
Lo juegan tres personas: un hombre (A), una mujer (B) y un interrogador (C), el cual puede pertenecer a cualquiera de ambos sexos. El interrogador permanece en una habitación que lo separa de las otras dos personas; su objetivo consiste en determinar cuál de las dos personas restantes es el hombre y cuál la mujer. Los conoce bajo los rótulos X e Y, y al final del juego declara, o bien “X es A e Y es B”, o bien “X es B e Y es A”. Se le permite plantear este tipo de preguntas a A y a B:
C: Por favor, X, ¿querría decirme cómo son de largos sus cabellos?
Supongamos ahora que X es A, y que debe contestar; su objetivo en el juego es conseguir que C no acierte la identificación. Su respuesta, en consecuencia, podría ser:
“Tengo un corte escalonado de cabello, y los mechones más largos miden un poco más de veinte centímetros”.
Para que el timbre de voz no pueda orientar el interrogador, las respuestas se darán por escrito o, mejor todavía, mecanografiadas. El dispositivo ideal sería una teleimpresora que comunique entre sí las dos habitaciones. Una alternativa posible es la intervención de un intermediario que transmita las preguntas y las respuestas. El objetivo del tercer jugador (B) es auxiliar al interrogador. Quizá su mejor estrategia sea brindar respuestas veraces, y puede agregar a sus respuestas expresiones tales como “La mujer soy yo, ¡no le haga caso a él!”, aunque esto no servirá de mucho en la medida en que el hombre puede decir cosas similares.
Y ahora, planteamos la pregunta: “¿Qué sucederá si A es sustituido por una máquina en este juego?”. ¿Las equivocaciones del interrogador tendrán la misma frecuencia, jugando de este modo, que cuando las contendientes son un hombre y una mujer? Estas interrogaciones remplazan a la formulada inicialmente: “¿Las máquinas pueden pensar?”.[2]
Después de haber explicado la naturaleza de su verificación, Turing pasa a hacer algunos comentarios sobre la misma que, teniendo en cuenta el año en que fueron formulados, llaman la atención por sus refinadas profundizaciones. Para comenzar, imagina un breve diálogo entre interrogador e interrogado:[3]
P: Por favor, escríbame un soneto a propósito del Puente de Forth [un puente sobre el Golfo de Forth, en Escocia].
R: Me declaro vencido. Jamás podría escribir poesía.
P: Sume 34957 y 70764.
R: (Pausa de unos treinta segundos) 105.621.
P: ¿Juega al ajedrez?
R: Sí.
P: Tengo R en R1R, y ninguna otra pieza. Usted tiene su R en R6R y T1T, además. Juega usted, ¿cómo mueve?
R: (Después de una pausa de 15 segundos) T8T, mate.
Pocos lectores advierten que, en el problema aritmético, no solamente hay una demora inusitada sino que, además, ¡la respuesta es errónea! Esto se explica fácilmente si quien responde es un ser humano: se trata de un simple error de cálculo. Pero si quien responde es una máquina, es posible una variedad de explicaciones. Algunas son éstas:
La reflexión sobre lo que Turing pueda haber querido significa mediante este toque sutil desemboca, poco más o menos, en los principales problemas filosóficos relacionados con Inteligencia Artificial.
Turing sigue adelante, señalando que
El nuevo problema tiene la ventaja de trazar una nítida delimitación entre las capacidades físicas e intelectuales del hombre… No le reprochamos a una máquina su ineptitud para sobresalir en un concurso de belleza, ni a un hombre el hecho de que pierda una carrera frente a un aeroplano.[4]
Uno de los atractivos del artículo consiste en ver cómo Turing sigue las huellas de cada una de las líneas de pensamiento, haciendo aflorar, frecuentemente, una aparente contradicción en algún estadio, para luego resolverla mediante el refinamiento de sus conceptos, en un nivel de análisis más profundo. Esta hondura de penetración en los problemas es la causa de que el artículo mantenga un valor destacado, luego de treinta años de enormes progresos en el desarrollo de las computadoras y de intensa actividad en 1 A. La cita que sigue es ilustrativa de esta rica movilización de las ideas en todas direcciones:
Quizá el juego pueda ser criticado desde el punto de vista de que las disparidades gravitan en exceso en contra de la máquina. Si el hombre se pusiera a tratar de ser la máquina, daría sin duda una exhibición muy pobre; sería descartado de inmediato por su lentitud e inexactitud aritméticas. ¿Las máquinas no pueden ejecutar determinadas cosas que deben ser descriptas como pensamiento, pero que son muy diferentes de lo que hace el hombre? Esta objeción es muy poderosa pero, al menos, podemos decir que no tenemos por qué preocupamos por ella si, pese a todo, puede llegar a construirse una máquina que practique satisfactoriamente el juego de la imitación.
Se podría postular que, cuando practique el “juego de la imitación”, la mejor estrategia de la máquina sería, posiblemente, hacer algo distinto a imitar el comportamiento humano. Quizá sea así, pero creo poco probable que se obtengan resultados muy eficaces a través de ello. De cualquier manera, no existe la intención, aquí, de investigar la teoría del juego, y se dará por supuesto que la mejor estrategia radica en tratar de suministrar respuestas del tipo de las que daría normalmente un hombre.[5]
Luego de propuesta y comentada la verificación, Turing observa:
Creo que la pregunta inicial, “¿Las máquinas pueden pensar?”, es demasiado carente de significado como para merecer que se la discuta. No obstante, pienso que a fines de este siglo el uso de las palabras y la opinión general de la gente educada se habrán modificado tanto que será posible hablar de máquinas pensantes sin esperar que se susciten contradicciones.[6]
Consciente de la tempestad de protestas que sin duda despertaría esta opinión, Turing procedió a detallar, en forma concisa y con ácido humor, una serie de objeciones a la noción de que las máquinas pudiesen pensar. Más abajo incluyo las nueve clases de objeción que él consideró, y combatió, junto con la descripción que hizo de ellas.[7] Lamentablemente, no contamos con espacio como para reproducir las ocurrentes e ingeniosas respuestas que formuló. El lector puede disfrutar evaluando por sí mismo las objeciones, y elaborando sus propias respuestas.
(1) La objeción teológica. El pensamiento es una función del alma inmortal del hombre. Dios ha dotado de un alma inmortal a todo hombre y a toda mujer, pero no a ningún otro animal ni a las máquinas. Luego, no hay animal o máquina que pueda pensar.
(2) La objeción “del avestruz”. Si las máquinas pensaran las consecuencias serian pavorosas. Debemos esperar y creer que ello no puede suceder.
(3) La objeción matemática. (Se trata, esencialmente, de la argumentación de Lucas.]
(4) La objeción de conciencia. “Sólo cuando una máquina pueda escribir un soneto o componer un concierto gracias a que experimenta pensamientos y emociones, y no por una reunión casual de símbolos, aceptaremos que la máquina se equipara con el cerebro en cuanto a que, además de enunciar algo, sabe que lo ha hecho. Ningún mecanismo (como no sea a través de meras señales artificiales: una simple estratagema) puede sentir complacencia ante sus propios aciertos, aflicción cuando se funden sus válvulas, halago cuando es elogiado, autosubestimación frente a sus equivocaciones, inquietudes sexuales, cólera o depresión cuando sus deseos no se cumplen”. [Cita de un tal profesor Jefferson.]
Turing se muestra convencido de que debe dar acabada respuesta, con el mayor detalle, a todas estas graves objeciones. Así, dedica muy buen espacio a su argumentación, dentro de la cual aparece otro breve diálogo hipotético:[8]
Interrogador: En la primera línea de su soneto, que dice “Eres cual un día estival”, ¿no sería lo mismo, o mejor, poner “un día primaveral”?
Testigo: Cambia el escandido.
Interrogador: ¿Y “un día invernal”? El escandido coincide perfectamente.
Testigo: Sí, pero a nadie le gusta que se lo asemeje a un día invernal.
Interrogador: ¿Diría usted que Mr. Pickwick le hace pensar en Navidad?
Testigo: En cierto modo.
Interrogador: Sin embargo, el de Navidad es un día invernal, y no creo que a Mr. Pickwick le moleste la comparación.
Testigo: No me parece que hable usted seriamente. Cuando se habla de un día invernal se hace alusión a un típico día de invierno, y no a un día especial como el de Navidad.
Después de este diálogo, Turing pregunta: “¿Qué diría el profesor Jefferson si la máquina de escribir sonetos le respondiese de viva voce algo semejante?”.
Las objeciones restantes:
(5) Argumentación de las diversas incapacidades. Este tipo de razonamiento adopta la siguiente forma: “Admito que pueda usted conseguir que las máquinas hagan todas las cosas que ha mencionado, pero usted nunca podrá conseguir que una máquina realice X.” Son sugeridos numerosos rasgos de X, a este respecto. Ofrezco una selección: ser afectuosa, ingeniosa, bella, amistosa, tener iniciativa, tener sentido del humor, discriminar entre aciertos y errores, cometer equivocaciones, enamorarse, gozar de las fresas con crema, hacer que alguien se enamore de ella, aprender de la experiencia, usar adecuadamente las palabras, ser el tema de sus propios pensamientos, tener un comportamiento tan diversificado como el de un hombre, hacer algo realmente nuevo.
(6) Objeción de Lady Lovelace. La información más detallada con que contamos sobre el Ingenio Analítico de Babbage proviene de una memoria al respecto de Lady Lovelace, quien incluye esta apreciación: “el Ingenio Analítico no tiene la pretensión de crear nada. Puede hacer todo aquello que sepamos cómo ordenarle que haga” (la cursiva es de Lady Lovelace).
(7) Argumento basado en la continuidad del sistema nervioso. El sistema nervioso no es, por cierto, una máquina de estados discretos. Un pequeño error en la información relativa a las dimensiones del impulso nervioso que llega a una neurona puede significar una gran diferencia en las dimensiones del impulso de salida. Siendo así, puede sostenerse que no cabe confiar en la posibilidad de imitar el comportamiento del sistema nervioso mediante un sistema de estados discretos.
(8) Argumento basado en la informalidad de la conducta. Dice, poco más o menos, así: “Si cada hombre tuviera un conjunto definido de reglas de conducta para regir su vida, no estaría por encima de la máquina.
Pero tales reglas no existen, de modo que los hombres no pueden ser máquinas.”
(9) Argumento basado en la percepción extrasensorial. Practiquemos el juego de la imitación, teniendo como testigo a un hombre calificado como receptor telepático. El interrogador puede plantear preguntas de esta clase: “¿A qué palo pertenece la carta que tengo en mi mano derecha?” El testigo, empleando la telepatía o la clarividencia, proporciona 130 respuestas correctas sobre 400 cartas. La máquina sólo puede hacer conjeturas al azar, y quizá obtenga 104 aciertos.
Como es fácil advertir, muchas de las objeciones se superponen y se asocian entre sí. En este libro, he pretendido dar respuesta, de un modo u otro, a la mayoría de aquéllas, aunque mucho menos concisamente, en general, que Turing.
Creo que la objeción (9) merece especial atención; también merece especial atención el hecho de que el trabajo de Turing haya sido reproducido, incluyéndolo en un libro, pero omitiendo dicha objeción. Mi punto de vista personal, opuesto al de Turing, es que la percepción extrasensorial no existe; Turing se resistía a aceptar la realidad de la misma, pero su admirable integridad científica lo llevó a considerarla, aceptando así los efectos de lo que él veía como una poderosa evidencia estadística en favor de la percepción extrasensorial. No estoy de acuerdo con este criterio, pese a lo cual estimo que se trata de una cuestión extraordinariamente compleja y atractiva.
En el diálogo que precede a este capítulo, hemos presentado un auténtico intercambio entre un programa de computadora y un ser humano. Ahora bien, ha habido muchos programas menos capaces de “conversar” que SHRDLU. Dos de ellos, bastante famosos, son el “Doctor”, creado por Joseph Weizenbaum, y “Parry”, invención de Kenneth Colby. Está previsto que el primero simule a un psiquiatra que utiliza una terapia “no directiva”, y que el segundo simule la estructura de creencias de un paranoico. Mediante una red especial se combinó un choque frontal entre ambos programas, del que ofrecemos a continuación una breve muestra:[9]
Parry: No comprendo sus razones.
Doctor: ¿Por qué no comprende mis razones?
Parry: ¿Debería comprenderlas?
Doctor: ¿Por qué dice eso en este momento?
Parry: Porque de eso se trata.
Doctor: Supongamos que se tratara de eso.
Parry: ¿Y entonces?
Doctor: Creo que no lo comprendo a usted muy bien.
Parry: Usted machaca demasiado con las mismas preguntas.
Doctor: ¿Y esa similitud entre las preguntas, qué le sugiere?
Parry: No lo entiendo a usted.
Doctor: ¿Querría entenderme?
Parry: Es por el interés que usted ha mostrado hacia mis sentimientos.
Doctor: ¡Oh! ¿He mostrado interés hacia sus sentimientos?
Estos programas, por supuesto, fueron ideados para hablar con seres humanos, de manera que su exhibición es bastante pobre aquí, donde han sido enfrentados entre sí. Principalmente, aquéllos se atienen a conjeturas sagaces acerca de la naturaleza de la entrada (que analizan muy superficialmente) y propinan respuestas seleccionadas con cuidado de entre un extenso repertorio previamente envasado. Las respuestas pueden estar envasadas sólo a medias: por ejemplo, un molde con espacios en blanco para llenar. Se da por supuesto que sus interlocutores humanos leerán allí muchas más cosas que las aceptadas por ellos mismos como efectivamente subyacentes al programa. En realidad, no es sino eso lo que sucede, según Weizenbaum, en su libro Computer Power and Human Reason, donde dice:
ELIZA [el programa a partir del cual fue elaborado el Doctor] creaba la más completa ilusión de haber penetrado en las mentes de las muchas personas que conversaban con él… Con frecuencia, éstas solicitaban que se les permitiese conversar con el sistema en privado; luego de hacerlo durante un rato, insistían, a pesar de mis explicaciones, en que la máquina, realmente, los había comprendido.[10]
Lo relatado en este pasaje puede parecer increíble. Aun así, es la verdad. Weizenbaum cuenta con una explicación:
La mayoría de los hombres no comprenden a las computadoras ni siquiera en una leve medida. Así, a menos que sean capaces de un muy gran escepticismo (el mismo que ejercitamos frente a una exhibición de magia), sólo pueden explicarse los logros intelectuales de las computadoras mediante la aplicación de la única analogía que está a su alcance: la que surge del modelo de su propia capacidad para pensar. No puede sorprender, entonces, que exageren las posibilidades; es verdaderamente imposible imaginar que un ser humano pueda imitar a ELIZA, por ejemplo, salvo que las aptitudes idiomáticas de ELIZA sean su límite.[11]
Esto equivale a la admisión de que esta clase de programa se basa en una perspicaz mixtura de bravata y estratagema audaz, volcadas a aprovecharse de la credulidad de la gente.
A la luz de este misterioso “efecto ELIZA”, hay quienes han propuesto la necesidad de revisar la verificación Turing, ya que, por lo visto, la gente puede ser embaucada mediante artificios simples. Se ha sugerido que el interrogador debiera ser un científico Premio Nobel. Podría ser más aconsejable llevar a sus últimas consecuencias la verificación Turing, e insistir en que el interrogador sea otra computadora. O bien, quizá, tenga que haber dos interrogadores —un ser humano y una computadora— y un testigo, y que sean los dos interrogadores quienes resuelvan si el testigo es otro ser humano u otra computadora.
Hablando más seriamente, tengo la impresión personal de que la verificación Turing, tal como fue formulada originalmente, es por completo razonable. En cuanto a las personas que, según Weizenbaum, fueron engañadas por ELIZA, no se les requirió que actuasen escépticamente, o que empleasen todo su talento en tratar de determinar si “quien” estaba tecleando era un ser humano o no. Creo que el grado de penetración de Turing en este problema ha sido profundo, y que su verificación, inalterada en lo sustancial, habrá de seguir vigente.
En las páginas que siguen, querría presentar la historia, encarada quizá desde un punto de vista heterodoxo, de algunos de los esfuerzos dedicados a descifrar los algoritmos que hay detrás de la inteligencia; ha habido allí fracasos y retrocesos, y los seguirá habiendo. Sin embargo, es mucho lo que podemos aprender de este excitante período.
Desde Pascal y Leibniz, los hombres vienen imaginando la posibilidad de máquinas que realicen tareas intelectuales. Durante el siglo diecinueve, Boole y De Morgan idearon “leyes del pensamiento” —el cálculo preposicional, sustancialmente— que significaron el primer paso hacia el software de IA; Charles Babbage, por su parte, inventó la primera “máquina de calcular”, convirtiéndose así en el precursor del hardware de las computadoras, y por consiguiente de IA. Se podría sostener que IA llega a la existencia en el momento en que las invenciones mecánicas toman a su cargo diversas tareas que, hasta entonces, únicamente eran realizables por la mente humana. No es fácil echar una mirada retrospectiva e imaginar los sentimientos experimentados por los primeros que presenciaron la ejecución, a cargo de engranajes, de sumas y multiplicaciones de grandes números. Quizá sintieron un temor reverente, al ver cómo fluían “pensamientos” de un hardware estrictamente físico. De todas maneras, sabemos que, casi un siglo después, cuando se construyeron las primeras computadoras electrónicas, sus inventores experimentaron el sentimiento místico y sobrecogido de encontrarse en presencia de otra clase de “ser pensante”. En qué medida había allí pensamiento real se planteó como un enorme enigma; aún hoy, varias décadas más tarde, este problema sigue siendo una fuente tanto de interés como de ferocidad polémica.
Es de hacer notar que, en la actualidad, prácticamente no hay quien sufra ya ese sentimiento de pavor, pese a que las computadoras efectúan operaciones increíblemente más sorprendentes que aquéllas capaces de provocar estremecimientos en las primeras épocas. La expresión otrora excitante de “Genio Electrónico Brillante” sólo se conserva como una suerte de clisé “demodé”, una huella risible de los tiempos de Flash Gordon y Buck Rogers. Es muy triste que nos sintamos blasé con tanta rapidez.
Hay un “Teorema” asociado al progreso de IA: una vez programada determinada función mental, la gente deja muy pronto de considerarla un ingrediente esencial del “pensamiento real”. El núcleo irrefutable de la inteligencia siempre reside en esa zona contigua que todavía no ha sido programada. Este “Teorema” me fue presentado por Larry Tesler, por lo cual lo llamaré Teorema de Tesler: “IA es todo aquello que todavía no ha sido concretado”.
Poco más abajo, se incluye un panorama selectivo de IA, que muestra los diversos dominios en los cuales han concentrado sus empeños los investigadores: cada uno manifiesta, a su modo particular, su requerimiento de convocar la quintaesencia de la inteligencia. Junto con algunos de los dominios, he incluido variantes adecuadas a los métodos empleados, o áreas de concentración más específicas.
Muchos de los tópicos precedentes no serán mencionados en los comentarios selectivos que haré más abajo, pero sin su inclusión la lista no sería completa. Los primeros tópicos están ubicados según un orden histórico. En cada uno de ellos, los esfuerzos iniciales desairaron las expectativas; por ejemplo, las complicaciones aparecidas en la traducción mecánica significaron una gran sorpresa para la mayoría de quienes habían creído que se trataba de una tarea directa, donde si bien sería arduo obtener la perfección, por cierto, la instrumentación básicas tendría que ser sencilla. Tal como se vio, la traducción es mucho más compleja que un diccionario de consulta y reordenamiento de palabras. No se trata, tampoco, de una dificultad causada por la falta de conocimiento de las expresiones idiomáticas. El hecho es que la traducción involucra la necesidad de contar con un modelo mental del mundo del cual se habla, y de manipular los símbolos de ese modelo. Un programa que no emplee un modelo del mundo cuando lea un determinado pasaje pronto se verá irremisiblemente atascado en ambigüedades y significados múltiples. Inclusive las personas —dotadas de una inmensa ventaja frente a las computadoras, ya que están totalmente equipadas con una comprensión del mundo— encuentran casi imposible traducir un texto a su propio idioma, cuando emplean para conseguirlo solamente un diccionario del idioma que no conocen. Así —y esto no es sorprendente, observando las cosas desde la actualidad—, el primer problema de IA condujo de inmediato a los problemas centrales de IA.
El ajedrez por computadoras, por su parte, probó también ser mucho más dificultoso de lo que habían sugerido las estimaciones intuitivas iniciales. De nuevo aquí resulta que el modo en que los seres humanos representan una situación ajedrecística en sus mentes es mucho más complejo que el mero conocimiento de cuál pieza está en cuál cuadro, asociado con el conocimiento de las reglas del juego. Dicho modo implica la percepción de configuraciones integradas por diversas piezas relacionadas entre sí, tanto como el conocimiento de heurísticas o reglas de oro, las cuales están vinculadas a aquellos bloques de alto nivel. Aunque las reglas heurísticas no son rigurosas al modo de las reglas oficiales, abren atajos que permiten la captación de lo que está sucediendo en el tablero, cosa que no ocurre con las reglas oficiales. Esto fue claramente reconocido desde el principio; sencillamente, se subestimaba la importancia del papel llenado por la comprensión intuitiva y en bloques del mundo ajedrecístico con respecto a la habilidad humana en este campo. Se predijo alguna vez que un programa dotado de determinada heurística básica, aunada a la velocidad deslumbrante y a la exactitud de una computadora para efectuar anticipaciones y analizar cada posible movida, derrotaría fácilmente a los jugadores humanos de más alto nivel: esta profecía, aun después de veinticinco años de intensos esfuerzos por parte de diversos equipos de investigación, está muy lejos de haberse cumplido.
En la actualidad, el problema ajedrecístico está siendo asediado desde diversos ángulos. Uno de los más recientes implica la hipótesis de que la anticipación es una cosa sin interés; en su lugar, uno debe limitarse a observar lo que ocurre en el tablero en un momento determinado y, empleando algo de heurística, idear un plan; luego, hay que hallar un movimiento que vaya poniendo en práctica dicho plan. Por supuesto, las reglas para la formulación de planes ajedrecísticos involucrarán necesariamente recursos heurísticos que son, en algún sentido, versiones “aplanadas” de la anticipación. Es decir, el equivalente de muchas experiencias de anticipación es “comprimido” bajo otra forma, la cual, aparentemente, no abarca la anticipación. En cierto sentido, lo que hay aquí es un juego de palabras; pero si el conocimiento “aplanado” aporta respuestas más eficaces que la anticipación real, aun cuando conduzca ocasionalmente a equivocaciones, algo se ha ganado. Ahora bien, esta destilación del conocimiento en formas perfeccionadas de utilización es precisamente algo en lo cual sobresale la inteligencia; luego, es probable que el ajedrez-no-anticipador sea una fructífera línea de investigación, a la que conviene impulsar. Sería particularmente atractivo diseñar un programa que pudiera, por sí mismo, convertir el conocimiento obtenido a través de la anticipación en reglas “aplanadas”: pero esto significa una tarea inmensa.
En realidad, un método semejante fue desarrollado por Arthur Samuel en su admirable programa jugador de damas. El recurso de Samuel consistió en usar medios tanto dinámicos (anticipación) como estáticos (sin anticipación) para la evaluación de cualquier situación dada de tablero. El método estático involucra una función matemática simple de diversas cantidades que caracterizan a cualquier posición de tablero, la cual puede, así, ser calculada casi instantáneamente; el método de evaluación dinámica implica la creación de un “árbol” de movidas posibles, respuestas a las mismas, respuestas a las respuestas, y así siguiendo (como fue mostrado en la figura 38). En la función de la evaluación estática habrá ciertos parámetros que pueden variar; tal variación tiene como consecuencia la generación de un conjunto de diferentes versiones posibles de la función mencionada. La estrategia de Samuel consistió en seleccionar, en forma evolutiva, valores cada vez mejores de aquellos parámetros.
Esto fue conseguido del siguiente modo: cada vez que el programa evaluaba una situación de tablero, lo hacía estática y dinámicamente. La respuesta surgida de la anticipación —llamémosla D— era utilizada para determinar la movida por hacer. El objetivo de E, la evaluación estática, era más artificioso: en cada movida, los parámetros variables eran levemente reajustados de modo que E se aproximará con la mayor exactitud posible a D. La consecuencia era la codificación parcial, en los valores de los parámetros de evaluación estática, del conocimiento obtenido dinámicamente gracias al trazado del árbol. En resumen, la idea era “aplanar” el complejo método de la evaluación dinámica dentro de la mucho más simple y eficaz función de evaluación estática.
Hay aquí un efecto recursivo muy delicado. La cuestión radica en que la evaluación dinámica de una posición de tablero determinada implica la anticipación de un número finito de movidas, digamos siete. Pero cada uno de los montones de posiciones de tablero que pueden producirse en siete ocasiones en esta proyección tienen que, a su vez, ser evaluados de alguna manera. Pero cuando el programa evalúa estas posiciones, ciertamente no puede anticipar otras siete movidas, pues debería anticipar catorce movidas, luego veintiuna, etc.: una regresión infinita. En lugar de ello, se apoya en la evaluación estática de las posiciones correspondientes a una proyección de siete movidas. Por lo tanto, en el esquema de Samuel tiene lugar un intrincado género de retroalimentación, donde el programa está tratando permanentemente de “aplanar” la evaluación anticipatoria dentro de una fórmula estática más simple; y esta fórmula, a su vez, juega un papel clave en la evaluación dinámica anticipatoria. Ambas vertientes, entonces, están íntimamente ligadas, y cada una aprovecha los perfeccionamientos logrados por la otra, de una manera recursiva.
El nivel de juego del programa de damas de Samuel es extraordinariamente elevado: equivalente al de los mejores jugadores del mundo. Si es así, ¿por qué no aplicar la misma técnica al ajedrez? Una comisión integrada por miembros de diversos países, incluyendo al matemático y gran maestro internacional danés Max Euwe, convocada en 1961 para estudiar la factibilidad del ajedrez por computadora, llegó a la desoladora conclusión de que la técnica de Samuel sería aproximadamente un millón de veces más difícil de aplicar al ajedrez que a las damas, y que esto parecía dar por cerrado el libro a este respecto.
La capacidad sumamente notable del programa de damas no puede ser tomada como base para decir: “la inteligencia ha sido lograda”; no obstante, tampoco se la debe minimizar. Es una combinación de penetraciones en lo que es el juego de damas, cómo pensar acerca de éste y cómo efectuar la programación. Hay quienes pueden sospechar que todo lo que aquélla muestra es la propia capacidad de Samuel para jugar a las damas. Pero esto no es cierto, cuando menos por dos razones: una, la de que los jugadores de damas de alta calidad determinan sus movidas con arreglo a procesos mentales que ellos mismos no comprenden en su totalidad: emplean sus intuiciones, y no existe ninguna forma conocida de arrojar luz sobre las propias intuiciones; cuando mucho, uno puede, por vía de introspección, apelar a la “impresión” o a la “metaintuición” —una intuición a propósito de las intuiciones propias— como guía, y tratar de describir a qué cree uno que se refieren las propias intuiciones. Pero esto no brindará sino una rudimentaria aproximación a la verdadera complejidad de los métodos Intuitivos. De aquí emana la certidumbre virtual de que Samuel no ha reflejado, en su programa, sus métodos personales de juego. La otra razón por la cual el juego que practica el programa de Samuel no debe ser confundido con el juego personal de Samuel es que Samuel no juega tan bien a las damas como su programa: éste le gana. Esto no es en absoluto paradójico; no más que el hecho de que una computadora programada para calcular π despiste a su programador vomitando, interminablemente, dígitos de π.
El problema de un programa que sobresale con respecto a su programador está vinculado con la cuestión de la “originalidad” en IA. ¿Qué sucede si un programa IA se aparece con una idea, o una línea táctica en un juego, que el programador jamás consideró? ¿A quién corresponde el mérito? Han ocurrido varios interesantes casos de este tipo, algunos en un nivel enteramente trivial, otros en un nivel mucho más profundo. Uno de los más célebres tuvo lugar con un programa para hallar demostraciones de teoremas, en el campo de la geometría euclidiana elemental, formulado por E. Gelernter. Un día, el programa obtuvo una demostración deslumbrantemente ingeniosa de uno de los teoremas fundamentales de la geometría, el denominado “pons asinorum” o “puente de peaje”.
Dice este teorema que los ángulos de la base de un triángulo isósceles son iguales. La prueba habitual requiere el trazado de una altura, la cual divide al triángulo en mitades simétricas. El elegante método descubierto por el programa (véase la figura 114) no empleó el trazado de ninguna línea. En lugar de ello, consideró al triángulo y a su imagen reflejada como dos triángulos diferentes. Luego, habiendo probado que ambos eran congruentes, señaló que los dos ángulos de la base se equiparaban entre sí en esta congruencia: quod erat demonstrandum.
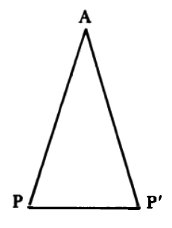
FIGURA 114. Prueba Pons Asinorum (descubierta por Pappus [~300] y el programa de Gelernter [~1960]). Problema: Mostrar que los ángulos de la base de un triángulo isósceles son iguales. Solución: Como el triángulo es isósceles, AP y AP′ tienen igual longitud. Por lo tanto, los triángulos PAP′ y P′AP son congruentes (lado-lado-lado). Esto implica que los ángulos correspondientes son iguales. Específicamente, los dos ángulos de la base son iguales.
Esta joya de demostración deleitó al creador del programa y a otras gentes; algunos vieron en ella evidencias de genialidad. Sin ánimo de empañar esta hazaña, digamos que, en el 300 d. C., el geómetra Pappus ya había descubierto esta demostración. De todas maneras, la interrogación sigue en pie: “¿A quién corresponde el mérito?”. ¿Esto es un comportamiento inteligente? ¿O la demostración se encontraba profundamente oculta en el ser humano (Gelernter), y la computadora se limitó a traerla a la superficie? Esta última pregunta se acerca al centro del blanco. Podemos invertirla: ¿La demostración se encontraba profundamente oculta en el programa? ¿O estaba próxima a la superficie? Es decir, ¿hasta qué punto es fácil ver por qué el programa actuó como actuó? ¿El descubrimiento puede ser atribuido a un mecanismo simple, o a una simple combinación de mecanismos, en el programa? ¿O hubo una compleja interacción que, aun cuando nos fuese explicada, no menguaría nuestra admiración reverencial cuando ocurriese?
Parece razonable presumir que, si uno puede atribuir el logro a determinadas operaciones que son fácilmente rastreables en el programa, en algún sentido, entonces, el programa sólo estaba revelando ideas escondidas en su esencia —aunque no muy profundamente— en la propia mente del programador. A la inversa, si el seguimiento del programa no sirve para esclarecernos en cuanto a por qué surgió este descubrimiento particular, quizá debiéramos comenzar a separar la “mente” del programa de la de su programador. Al ser humano le corresponde el mérito de haber inventado el programa, pero no por haber tenido en su propia cabeza las ideas producidas por el programa. Entonces, podemos decir que el ser humano es el “metautor” —el autor del autor del resultado— y que el programa es (lisa y llanamente) el autor.
En el caso particular de Gelernter y su máquina de geometría, es probable que Gelernter no hubiera redescubierto la demostración de Pappus; sin embargo, los mecanismos que generaron la demostración se encontraban lo suficientemente próximos a la superficie como para que uno vacile en decir que el programa es un geómetra por derecho propio. Si aquél hubiera continuado asombrando mediante el hallazgo repetido de nuevas demostraciones ingeniosas, cada una de las cuales diese la impresión de brotar de un nuevo chispazo de genialidad, y no de un método estándar, uno no tendría escrúpulo alguno, entonces, en llamar geómetra al programa: pero no es esto lo que ha sucedido.
La distinción entre autor y metautor es nítidamente establecida en el caso de la composición de música por computadora. En el acto de la composición, un programa puede impresionar como poseedor de diversos niveles de autonomía. Un nivel es ejemplificado por una pieza cuyo “metautor” es Max Mathews, de Bell Laboratories, quien tomó las partituras de dos marchas, “When Johnny Comes Marching Home” y “The British Grenadiers”, e instruyó a la computadora para que elaborara una nueva partitura, la cual debía comenzar como “Johnny” y luego, lentamente, identificarse con “Grenadiers”. A mitad del transcurso de la pieza, “Johnny” se extingue por completo, y lo que se oye es “Grenadiers”… Entonces, el proceso se invierte, y la pieza finaliza con “Johnny”, reiterando la situación del comienzo. Según las propias palabras de Mathews, esto es
… una nauseabunda experiencia musical, aunque no carente de interés, particularmente en materia de conversiones rítmicas. “The Grenadiers” está compuesta en tiempo de 2/4, en la tonalidad de Fa mayor. “Johnny” está compuesta en tiempo de 6/8, en la tonalidad de Mi menor. El cambio de 2/4 a 6/8 puede ser apreciado con claridad, pero a un músico humano le sería muy difícil ejecutarlo. La modulación de la tonalidad de Fa mayor a la de Mi menor, que implica un cambio de dos notas en la escala, es discordante; sin duda, una transición más breve habría sido una elección mejor.[12]
La pieza resultante tiene la cualidad de ser un tanto festiva, pese a que por momentos es pomposa y confusa.
¿Lo que está haciendo la computadora es componer? Lo mejor sería que esta pregunta no apareciese, pero no puede ser completamente ignorada. Es difícil suministrar una respuesta. Los algoritmos son deterministas, simples y comprensibles. No hay envueltas computaciones complicadas o de ardua comprensión; no se ha utilizado ningún programa de “aprendizaje”; no ocurre ningún proceso fortuito; la máquina funciona de manera perfectamente mecánica y normal. Empero, el resultado es una secuencia de sonidos que, en el orden de los detalles finos, no ha sido prevista por el compositor, aunque la estructura global del fragmento haya sido completa y precisamente especificada. Así, el compositor se ve a menudo sorprendido, y gratamente, por los detalles que dan concreción a sus ideas. Es solamente en esta medida que la computadora compone. Llamamos composición al proceso algorítmico, pero de inmediato volvemos a subrayar que los algoritmos son transparentemente simples.[13]
Ésta es la respuesta de Mathews a una pregunta que él preferiría marginar. Pese al carácter negativo de esta respuesta, mucha gente halla más sencillo decir simplemente que la pieza fue “compuesta por una computadora”. Creo que esta expresión desfigura totalmente la situación. El programa carece de estructuras análogas a los “símbolos” del cerebro, por lo cual no se puede afirmar, en el sentido que fuere, que está “pensando” en lo que está haciendo. Atribuir la composición de este género de pieza musical a la computadora sería como atribuir la autoría de este libro a la máquina, computada automáticamente, de fotocomposición con espacios compensados (incorrectamente, a menudo), con la que se compone.
Esto plantea una pregunta que constituye una ligera digresión con respecto a IA, para nada enorme, de verdad. Cuando vemos las formas “yo”, “mí” o “me” en un texto, ¿a qué las referimos? Por ejemplo, pensemos en la expresión “LÁVAME”, que a veces se ve en la parte de atrás de nada limpios camiones de carga. ¿Quién es este “me”? ¿Es el reclamo de un niño mal atendido, quien, desesperado por gozar de un baño, escribió aquella palabra en la primera superficie que encontró? ¿O es el camión el que reclama un baño? ¿O, tal vez, sea la expresión misma, deseosa de tomar una ducha? ¿O será que nuestro idioma está pidiendo que se lo purifique? Se podría seguir y seguir en este juego de conjeturas. En el caso presente, la expresión es bromista, destinada a hacer suponer, en determinado nivel, que el camión mismo la ha escrito para exigir una buena lavada. En otro nivel, uno reconoce la inscripción como si fuera formulada por un niño, y disfruta lo gracioso de la malinterpretación. Lo que tenemos aquí, en realidad, es un juego basado en la lectura de “me” en un nivel erróneo.
Esta clase de ambigüedad, precisamente, aparece en este libro, primero en el Contracrostipunctus, y después en las exposiciones relativas a la cadena G de Gödel (y sus familiares). La interpretación dada a los discos no pinchables rezaba: “No puedo ser escuchado mediante el Fonógrafo X”, y la correspondiente a los enunciados indemostrables era: “No puedo ser demostrado en el Sistema Formal X”. Tomemos esta última oración: ¿en qué otra ocasión, si es que hubo alguna, nos hemos topado con una oración cuyo “yo” —tácito, en este caso— nos hace entender automáticamente que no se refiere al emisor de la oración, sino a la oración misma? Presumo que muy poco frecuentemente. Cuando la palabra “yo” aparece en un soneto de Shakespeare no está haciendo referencia a una forma poética de catorce versos, impresa en una página, sino a un ser de carne y hueso ubicado tras el escenario, en algún sitio entre bambalinas.
¿Hasta dónde rastreamos, por lo común, el “yo” de una oración? La respuesta, según creo, es que buscamos un ser consciente a quien adjudicarle la autoría de aquélla. Pero, ¿qué es un ser consciente? Alguna cosa en la cual podamos proyectarnos con comodidad. En el programa “Doctor” de Weizenbaum, ¿hay una personalidad? Si es así, ¿la personalidad de quién? Un breve debate sobre esta misma pregunta se suscitó hace poco en las páginas de la revista Science.
Esto nos devuelve al problema del “quien” que compone la música de computadora. En la mayoría de las ocasiones, la fuerza conductora que hay detrás de ese tipo de piezas es un intelecto humano, y la función de la computadora reside en su utilización, con mayor o menor ingenuidad, como herramienta que concrete una idea creada por un ser humano. El programa que cumple este propósito no tiene nada con lo cual podamos identificarnos. Es una simple y monofuncional pieza de hardware, carente de flexibilidad, de perspectiva acerca de lo que está haciendo, y de sentido de sí misma. No obstante, si la gente desarrolla programas que tengan esos atributos, y de ellos comienzan a surgir piezas de música, una tras otra, habrá llegado el momento indicado para repartir nuestra admiración: parte para el programador, por crear un programa tan pasmoso, y parte para el programa mismo por su sentido musical. Se me ocurre que esto tendrá lugar únicamente cuando la estructura interna de un programa de esta clase se base en algo similar a los símbolos de nuestro cerebro y a sus patrones de desencadenamiento, los cuales son responsables de la compleja noción de significación. El hecho de tener este género de estructura interna dotaría al programa de propiedades que nos permitirían identificarnos cómodamente con él, en alguna medida. Entretanto, no nos sentiremos cómodos diciendo “esta pieza fue compuesta por una computadora”.
Retornemos a la historia de IA. Una de las primeras que se intentaron programar fue la actividad intelectual de demostrar teoremas. Conceptualmente, esto no difiere de programar una computadora para que persiga una derivación de MU en el sistema MIU, salvo que los sistemas formales involucrados allí eran por lo común más complicados que el sistema MIU. Se trataba de versiones del cálculo de predicados, el cual es una extensión del cálculo preposicional que abarca cuantificadores. La mayor parte de las reglas del cálculo de predicados fue incluida, en realidad, en TNT. Un recurso promisorio, cuando es formulado un programa así, consiste en infundirle un sentido de dirección, de modo que, en lugar de vagar por todo el campo, el programa actúe exclusivamente dentro de recorridos “pertinentes”: aquellos que, por aplicación de algún criterio razonable, parecen conducir hacia la cadena buscada.
En este libro no hemos tenido mayor contacto con tales problemas. Por cierto, ¿cómo saber cuándo se está avanzando hacia un teorema, y cómo asegurarse de no estar disparando con cartuchos vacíos? Esto es algo que yo confié en ilustrar mediante el acertijo MU. Ciertamente, no puede haber respuesta definitiva: tal es el contenido de los Teoremas limitativos, puesto que si siempre se pudiese saber qué camino seguir, se podría construir un algoritmo para la demostración del teorema que se quiera, y ello sería violatorio del Teorema de Church. No existe semejante algoritmo. (Dejo a cargo del lector advertir con exactitud por qué se desprende esto del Teorema de Church). Con todo, lo anterior no significa que sea totalmente imposible desarrollar ninguna intuición relativa a cuál es y a cuál no es una ruta más fértil; en los hechos, los mejores programas cuentan con una heurística muy elaborada, que les permite efectuar deducciones en materia de cálculo de predicados a velocidades comparables a las de los seres humanos expertos.
El mejor expediente para la demostración teoremática es utilizar el hecho de que se tiene un objetivo global —la cadena que se desea producir— gracias al cual orientarse localmente. Una técnica desarrollada para transformar objetivos globales en estrategias de derivación locales ha recibido el nombre de reducción del problema. Está basada en la idea de que, cuando se persigue un objetivo de largo alcance, existen por lo general subobjetivos cuyo cumplimiento contribuirá al del objetivo principal. Por consiguiente, si uno fragmenta un problema dado en una serie de subproblemas, y luego divide éstos en subsubproblemas, y así siguiendo, de manera recursiva, obtendrá finalmente objetivos sumamente modestos que, presumiblemente, podrán ser satisfechos con un par de pasos. Al menos, así pareciera ser…
La reducción del problema puso a Zenón en un gran apuro. Como se recordará, el método de Zenón para llegar a B, desde A (siendo B, en consecuencia, el objetivo), consiste en “reducir” el problema a dos subproblemas: recorrer primero la mitad del camino, y luego la otra mitad. Ahora, pues, tenemos que han sido “desplazados” —en el sentido del Capítulo V— dos subobjetivos hacia la “pila de objetivos”. Cada uno de éstos, a su vez, será sustituido por dos subsubobjetivos, y así ad infinitum. Se acabará contando con una pila de objetivos infinita, en lugar de un objetivo único (figura 115). Recuperar un número finito de objetivos acumulados en la pila se demostrará una tarea llena de resbalosas complicaciones… lo cual es, precisamente, el conflicto de Zenón.
Otro ejemplo de recursividad infinita en una reducción del problema se presenta en el diálogo Pequeño Laberinto Armónico, cuando Aquiles pide que se le conceda un Deseo Atipo. La concesión de éste debe ser postergada hasta que se obtenga la autorización de la Meta-Genio; pero ésta, a su vez, debe ser autorizada a dar autorización, para conseguir lo cual invoca al Meta-Meta-Genio,… etc. Pese a la infinitud de la pila de objetivos, a Aquiles se le concedió su deseo. ¡Victoria de la reducción del problema!
FIGURA 115. Árbol sin fin del objetivo de Zenón, para ir de A a B.
Fuera de toda broma, se ha de reconocer que la reducción del problema es una técnica eficaz para transformar problemas globales en problemas locales. Se distingue en ciertas situaciones, como por ejemplo en la persecución de propósitos en el juego de ajedrez, allí donde la técnica anticipatoria rinde a menudo resultados muy pobres, aun siendo llevada a extensiones risibles, tales como de quince dobleces o más. Esto se debe a que la técnica anticipatoria no está basada en el planeamiento; sencillamente, carece de objetivos y explora una enorme cantidad de posibilidades inertes. Contar con un objetivo facilita el desarrollo de una estrategias para el logro del mismo, lo cual configura una filosofía totalmente distinta a la de la anticipación mecánica. Por supuesto, en la técnica anticipatoria la conveniencia o inconveniencia es medida por la función de evaluación de las posiciones, y ello incorpora, indirectamente, una cantidad de objetivos, en forma principal el de evitar el jaque mate. Pero esto es demasiado indirecto. Los buenos jugadores de ajedrez que han competido con programas de anticipación quedan con la impresión de que estos últimos son muy débiles en cuanto a la formulación de planes o de estrategias.
No hay garantías de que el método de reducción de problemas funcione; en muchas ocasiones fracasa. Consideremos, por ejemplo, un problema sencillo: imagine el lector que es un perro, y que un ser humano amigo le ha arrojado su hueso predilecto en otro patio, separado de usted por una cerca de alambre. Usted puede ver su hueso a través de los hilos metálicos, ¡esa exquisitez, reposando allí sobre la hierba! Hay una puerta abierta en la cerca, situada a unos veinte metros del hueso. ¿Qué hace usted? Algunos perros se acercan a la valla, se detienen junto a ella, y se ponen a ladrar; otros se precipitan hacia la puerta y corren de vuelta hasta el encantador hueso. Puede decirse que ambos perros han puesto en práctica la técnica de la reducción del problema; pero cada uno de ellos ha representado el problema, en su mente, de manera distinta, y allí reside toda la diferencia. El perro que ladra ve así los subproblemas: (1) acercarse a la valla; (2) atravesarla, y (3) llegar hasta el hueso… pero ese subproblema (2) es un “problemón”, y de allí los ladridos. El otro perro subdivide así: (1) llegar a la puerta; (2) atravesarla; (3) llegar hasta el hueso. Adviértase que todo depende del modo en que sea representado el “espacio del problema”, es decir, de lo que uno perciba como “reductor” del problema (movimiento hacia adelante que acerca al objetivo global), y como “magnificador” del problema (movimiento hacia atrás que aleja del objetivo).
Algunos perros intentan dirigirse primero, directamente, hacia el hueso, y cuando se topan con la cerca, algo se enciende en su cerebro: no demoran en cambiar de curso, y encaminarse hacia la puerta. Estos perros entienden que, lo que a primera vista parecía que incrementaba la distancia entre la situación inicial y la perseguida —a saber, el alejarse del hueso pero aproximarse a la puerta—, en realidad la hace decrecer. Al comienzo, confunden la distancia física con la distancia del problema. Cualquier movimiento que aleje del hueso parece, por definición, una Mala Cosa; pero luego —de alguna manera— comprenden que pueden cambiar su percepción acerca de qué los llevará “más cerca” del hueso. En un espacio abstracto adecuadamente elegido, ¡moverse hacia la puerta es una trayectoria que lleva al perro más cerca del hueso! En todo momento, el perro está situándose “más cerca” —en este nuevo sentido— del hueso. De este modo, la utilidad de la reducción del problema depende de cómo nos representamos mentalmente el problema del cual se trate. Lo que en un espacio parece un retroceso, en otro puede verse como un revolucionario paso adelante.
En la vida cotidiana, constantemente enfrentamos y resolvemos variantes del problema perro-hueso. Por ejemplo, si una tarde decido trasladarme ciento cincuenta kilómetros hacia el sur, pero estoy en mi oficina, a la cual he ido en bicicleta, tengo que efectuar una cantidad sumamente extensa de movimientos hacia direcciones aparentemente “erróneas” antes de encontrarme encaminado, a bordo de un automóvil, directamente hacia el sur. Tengo que dejar mi oficina, lo que significa, digamos, dirigirme unos pasos al este, y atravesar luego la antesala del edificio, lo cual requiere moverse hacia el norte, y luego hacia el oeste. Después, tomo la bicicleta y emprendo la marcha hacia mi casa: esto implica desplazamientos hacia todas las direcciones del compás. Completado este recorrido, debo realizar una sucesión de movimientos breves hasta que por fin abordo mi automóvil, y salgo. Por supuesto, no estaré rumbo al sur de inmediato, ya que opto por un recorrido que puede incluir ciertos avances hacia el norte, el oeste o el este, con la finalidad de llegar cuanto antes a la carretera.
Todo esto no es sentido como paradójico, en lo más mínimo, ni provoca ningún sentimiento de extrañeza. El espacio dentro del cual el retroceso físico es percibido como movimiento directo hacia el objetivo está asentado tan profundamente en mi mente que no encuentro nada raro cuando estoy recorriendo un tramo hacia el norte. Los pasillos, calles, etc., actúan como canales que acepto sin gran resistencia, de modo que una parte del acto de decidir cómo percibir la situación implica simplemente la aceptación de lo que es impuesto. Sin embargo, a veces los perros situados frente a la cerca tienen gran dificultad para proceder así, especialmente si el hueso está muy próximo a ellos, totalmente a la vista y exhibiendo un aspecto altamente apetitoso. Y, cuando el espacio del problema es sólo ligeramente diferente del espacio físico, es común que las personas no atinen a acertar con lo que cabe hacer, tal cual como los perros que se ponen a ladrar.
En algún sentido, todos los problemas son versiones abstractas del problema perro-hueso. Muchos problemas no residen en el espacio físico sino en determinado género de espacio conceptual. Cuando se comprende que el desplazamiento directo hacia el objetivo llevará a toparse con alguna suerte de “cerca” abstracta, es posible optar por una de dos cosas: (1) comenzar a alejarse del objetivo, a través de movimientos más bien casuales, a la espera de hallar una “puerta” oculta que pueda ser atravesada, lo que dejaría expedito el camino hacia el hueso; o (2) tratar de descubrir un nuevo “espacio” dentro del cual poder representar el problema, y donde no exista ninguna cerca abstracta que aísle el objetivo; luego, se podrá avanzar directamente hacia éste, en ese nuevo espacio. El primer método puede impresionar como una forma holgazana de proceder, y el segundo como una forma difícil y complicada. No obstante, las soluciones que involucran la restructuración del espacio del problema aparecen frecuentemente bajo la forma de súbitos relámpagos de penetración, antes que como productos de lentos y deliberados procesos de pensamiento. Es probable que estos relámpagos intuitivos provengan del corazón mismo de la inteligencia y, obvio es decirlo, su fuente es un secreto rigurosamente protegido de nuestro receloso cerebro.
En cualquier caso, la cuestión no reside en que la reducción del problema, per se, conduzca a resultados negativos; es una técnica cabalmente eficaz. El dilema es más profundo: ¿cómo establecer una adecuada representación interna de un problema? ¿Qué clase de “espacio” es el que se ha de considerar? ¿Qué tipos de acción reducen la “distancia” que nos separa del objetivo, en el espacio por el cual hemos optado? Esto puede ser expresado en lenguaje matemático como la búsqueda de una adecuada métrica (función de distancia) entre estados. Se necesita descubrir una métrica en la cual la distancia entre nosotros y nuestro objetivo sea muy corta.
Ahora bien, puesto que este asunto de determinar una representación interna es, en sí mismo, un tipo de problema, ¡deberíamos tratar de aplicarle la técnica de reducción del problema! Para conseguirlo, deberíamos contar con la posibilidad de representar una inmensa variedad de espacios abstractos, lo cual significa un proyecto extraordinariamente complejo. No estoy enterado de que nadie haya intentado algo semejante; quizá se trate tan sólo de una atractiva y curiosa propuesta teórica pero totalmente irreal, en los hechos. De todas maneras, en IA hay una angustiosa carencia de programas que puedan “retornar sobre sus pasos” y echar un vistazo sobre lo que están haciendo, de donde surgiría una perspectiva que los reorientaría con respecto a la tarea entre manos. Una cosa es formular un programa que vaya más allá de una tarea única que, si es cumplida por un ser humano, parece requerir inteligencia, ¡y otra cosa absolutamente distinta formular un programa inteligente! Es la diferencia entre la avispa Sphex (véase Capítulo XI), cuya rutina rígida ofrece la apariencia engañosa de una gran inteligencia, y un ser humano que esté observando la avispa Sphex.
Un programa inteligente debería ser, presumiblemente, aquél lo suficientemente versátil como para resolver problemas de muy diferente índole. Aprendería a conseguirlo de un modo distinto en cada caso y ello le significaría la acumulación de experiencia. Sería capaz de funcionar dentro de un juego de reglas pero también, en los momentos indicados, volvería sobre lo actuado y elaboraría una estimación acerca de si tal juego de reglas tiene la aptitud necesaria, con relación al conjunto global de objetivos que se persiguen. Sería capaz de detener el funcionamiento dentro de una sistemática determinada y, si es necesario, crear un nuevo sistema de reglas para que enmarquen, durante un lapso, el trabajo.
Muchas de estas reflexiones pueden hacer pensar en rasgos del acertijo MU. Por ejemplo, alejarse del objetivo de un problema recuerda el movimiento que aleja de MU mediante la construcción de cadenas más y más largas, de las que se espera puedan conducir, indirectamente, a la obtención de MU. Si uno es un “perro” ingenuo, sentirá que se está alejando de su “hueso MU” toda vez que su cadena se agrande en más de dos caracteres; si, en cambio, se es un perro más sutil, se verá en el empleo de las reglas de ampliación un fundamento indirecto, algo así como la orientación hacia la puerta que lleva al hueso MU.
Hay otras conexiones con el acertijo MU, tales como las dos modalidades de operación que permiten internarse en la naturaleza del acertijo: la vía Mecánica y la vía Inteligente. En la primera, uno se encaja en el interior de determinado enmarcamiento fijo; en la segunda, siempre es posible alejarse unos pasos y observar panorámicamente las cosas. Esto último equivale a elegir una representación dentro de la cual actuar; y actuar dentro de las reglas del sistema es equivalente a ensayar la técnica de la reducción del problema en el interior de tal enmarcamiento seleccionado. Los comentarios de Hardy a propósito del estilo de Ramanuyan —en particular, su disposición a modificar sus propias hipótesis— ilustran esta interacción, en el pensamiento creativo, entre la vía M y la vía I.
La avispa Sphex opera magníficamente en la vía M, pero carece de toda habilidad para elegir su enmarcamiento o, inclusive, para modificar en lo más mínimo su vía M. Tampoco es capaz de advertir que está ocurriendo una y otra vez la misma cosa en su sistema, pues advertirlo constituiría un brinco fuera del sistema, por muy pequeña que fuere la medida en que ello ocurra. Lisa y llanamente, la avispa no se percata de la similitud de las repeticiones. Este fenómeno (el de no caer en la cuenta de la identidad que caracteriza a ciertos hechos repetitivos) se vuelve interesante cuando nos lo aplicamos a nosotros mismos. ¿Existen situaciones repetidas, que se producen muchas veces en nuestras vidas y a las que manejamos en cada ocasión de la misma tonta manera, porque carecemos de la amplitud de panorama necesaria paras percibir su similitud? Esto nos lleva de nuevo a aquel tema recurrente, “¿Qué es la similitud?”. Pronto lo veremos reaparecer bajo la forma de problema de IA, y entonces hablaremos de los patrones de reconocimiento.
Desde diversos puntos de vista, la matemática es un dominio sumamente interesante para ser estudiado a partir del enfoque de IA. Todos los matemáticos tienen la sospecha de que hay algunas clase de métrica entre las ideas matemáticas, es decir, que toda la matemática es una red de conclusiones entre las cuales existe una enorme cantidad de vínculos. En esa red, algunas ideas están relacionadas muy estrechamente, en tanto que otras son asociadas gracias a recorridos más elaborados. En ocasiones, dos teoremas matemáticos se encuentran muy próximos porque uno de ellos puede ser demostrado con facilidad, dado el otro. Otras veces, son dos ideas las que se aproximan, porque son análogas, o inclusive isomórficas. Se trata de dos sentidos diferentes de la palabra “próximo” en el dominio de la matemática; es probable que haya muchos otros. Es difícil decidir si nuestro sentido de la proximidad matemática está dotado de objetividad, o universalidad, o bien si es, en su mayor medida, un accidente del desarrollo histórico. Ciertos teoremas pertenecientes a ramas distintas de la matemática nos impresionan como de muy ardua vinculación, y podríamos concluir que no están relacionados: pero más tarde aparece algo que nos obliga a modificar ese concepto. Si pudiéramos implantar nuestro altamente desarrollado sentido de la proximidad matemática —una “métrica mental de matemático”, por así decir— en un programa, tal vez pudiéramos producir un “matemático artificial”. Pero ello depende de que se esté en condiciones de infundir también un sentido de simplicidad, o “naturalidad”, lo cual constituye otro gran obstáculo.
Estos temas han sido afrontados en muchos proyectos de IA. Hay una serie de programas desarrollados en el Instituto Tecnológico de Massachusetts, bajo el nombre de “MACSYMA”, cuyo propósito es auxiliar a la matemática en la manipulación simbólica de expresiones matemáticas complejas. Este programa cuenta con un sentido de “adónde dirigirse”, una suerte de “gradiente de complejidad” que lo guía desde las expresiones complejas por lo general así consideradas hasta las más simples. Forma parte del repertorio de MACSYMA un programa denominado “SIN”, que efectúa integración simbólica de funciones, del cual se reconoce, casi sin excepciones, que supera a los seres humanos en determinadas categorías. Se apoya en un conjunto de aptitudes diferentes, tal como debe estarlo la inteligencia, en general: un vasto cuerpo de conocimientos, la técnica de reducción de problemas, una gran cantidad de recursos heurísticos, y también algunos recursos especiales.
Otro programa, formulado por Douglas Lenat, en Stanford, tiene como propósito inventar conceptos y descubrir hechos en el campo de la matemática muy elemental. Comenzando con la noción de conjuntos, y una colección de nociones sobre lo que resulta de “interés” retener de aquélla, “inventó” la idea de contar, luego la de sumar, luego la multiplicación, luego —entre otras cosas— la noción de número primo, ¡y llegó nada menos que a redescubrir la conjetura Goldbach! Claro que todos estos “descubrimientos” tienen una antigüedad de centenares —de miles, inclusive— de años. Quizá esto pueda ser explicado, en parte, diciendo que el sentido de lo “interesante” fue transmitido por Lenat a una gran cantidad de reglas, las cuales pueden haber recogido el nivel formativo de aquél, propio del siglo veinte; como sea, se trata de algo impresionante. El programa pareció perder su impulso luego de su muy respetable hazaña. Una cosa interesante, con relación a ello, es que fue incapaz de desarrollar o de perfeccionar su propio sentido de lo que es interesante. Esto sugiere un nivel más alto de dificultad, o varios niveles más, posiblemente.
Muchos de los ejemplos anteriores han sido citados a fin de subrayar que la forma en que es representado un dominio se sustenta grandemente en el modo en que ese dominio es “comprendido”. Un programa que se limite a dar salida impresa, en un orden preestablecido, a teoremas de TNT, carecería de toda compresión de la teoría de los números; un programa como el de Lenat, con sus estratos adicionales de conocimiento, puede merecer que se lo considere poseedor de un sentido rudimentario de teoría de los números; y un programa que incorpore el conocimiento matemático a un contexto amplio de experiencia del mundo real probablemente sea el más capacitado para “comprender”, en el sentido en que nosotros creemos que lo hacemos. Esta representación del conocimiento es la cuestión esencial en IA.
En las primeras épocas se supuso que el conocimiento se presentaba en oraciones semejantes a “paquetes”, y que por lo tanto el mejor medio para implantar conocimiento en un programa consistía en desarrollar una forma simple de traducir hechos a pequeños paquetes pasivos de datos. Después, cada hecho sería simplemente una pieza de datos, disponibles para su utilización por los programas. Esto es ejemplificado por los programas de ajedrez, donde las posiciones de tablero son codificadas en matrices o listas de cierto tipo, y almacenadas eficientemente en la memoria, de donde pueden ser recuperadas y accionadas mediante el empleo de subrutinas.
El hecho de que el ser humano almacene hechos de una manera más complicada era algo conocido desde hace mucho por los psicólogos, y descubierto sólo en épocas recientes por la investigación en IA, la cual se encuentra ahora estudiando los problemas del conocimiento articulado uen bloques”» y la diferencia entre tipos procedimentales y declarativos de conocimiento, la cual se relaciona, como vimos en el Capítulo XI, con la diferencia entre el conocimiento accesible a la introspección, y el inaccesible a esta última.
La concepción ingenua de que todo conocimiento debía ser codificado en piezas pasivas de datos es contradicha, en verdad, por el hecho más fundamental en materia de diseño de computadoras, a saber: cómo efectuar sumas, restas, multiplicaciones, etc., no es algo codificado en piezas de datos y almacenado en la memoria; no está representado en ninguna parte de la memoria, sino en los patrones interconectados del hardware. Una calculadora de bolsillo no almacena en su memoria el conocimiento de cómo sumar; este conocimiento está codificado en sus “vísceras”. No existe ningún punto en la memoria que pueda ser señalado si alguien pregunta: “¿Puede mostrarme dónde está localizado el conocimiento de cómo efectuar sumas, en esta máquina?”.
Sin embargo, son muchos los esfuerzos que se han aplicado en IA a sistemas en los cuales la masa de conocimiento ha sido almacenada en lugares específicos, es decir, declarativamente. No hace falta decir que algún conocimiento tiene que ser incorporado a los programas, pues de otra manera no serían programas en absoluto, sino meras enciclopedias. El asunto es cómo repartir el conocimiento entre programa y datos; no es que sea fácil, en todos los casos, distinguir entre programa y datos, de ninguna manera: espero que ello haya quedado suficientemente claro en el Capítulo XVI. Así y todo, en el desarrollo de un sistema, si el programador concibe intuitivamente algún ítem específico como dato (o como programa), eso puede tener repercusiones significativas en la estructura del sistema, porque cuando un programa tiende a distinguir entre objetos semejantes de datos y objetos semejantes a programas.
Es importante puntualizar que, en principio, cualquier manera de codificación de la información en estructuras de datos o en procedimientos es tan buena como otra, en el sentido de que si no se está excesivamente preocupado por la eficacia se puede utilizar un esquema u otro. No obstante, se pueden aportar razones que indican que uno de los métodos es definitivamente superior al otro. Consideremos, por ejemplo, el alegato siguiente en favor del empleo exclusivo de representaciones procedimientales: “En cuanto se intenta codificar aspectos de determinada complejidad como datos, se está obligado a desarrollar el equivalente de un nuevo lenguaje, o formalismo. Así, en los hechos, la estructura de datos se transforma en algo semejante a un programa, con alguna pieza del programa en función de intérprete; es perfectamente posible representar en forma directa la misma información, desde el comienzo, en forma procedimental, y obviar ese nivel adicional de interpretación”.
La argumentación anterior suena muy convincente, pero si es interpretada con alguna extensión, puede ser tomada como un razonamiento en contra del ADN y del ARN. ¿Por qué codificar la información genética en el ADN, si representándola directamente en las proteínas eliminaríamos no uno, sino dos niveles de interpretación? La respuesta es: ocurre que resulta sumamente provechoso contar con la misma información en varias formas diferentes, con vistas a diferentes fines. Una ventaja del almacenamiento de información genética en la forma modular, y semejante a la de los datos, del ADN, es que dos genes individuales pueden ser recombinados fácilmente a efectos de formar un nuevo genotipo. Esto sería muy dificultoso si la información se encontrara en las proteínas. Una segunda razón para el almacenamiento de la información en el ADN es que su transcripción y traducción a proteínas es sencilla. Cuando ello no es necesario, no ocupa mucho lugar y, cuando es necesario, sirve como molde. No existe ningún mecanismo que copie una proteína a partir de otra; los dobleces de su estructura ternaria harían del copiado una tarea muy pesada. Complementariamente, es casi forzoso que sea posible el vuelco de información genética a estructuras tridimensionales tales como las enzimas, porque el reconocimiento y manipulación de moléculas es, por naturaleza, una operación tridimensional. En consecuencia, el alegato en favor de la exclusividad de las representaciones procedimentales pierde todo fundamento en el contexto celular. Surge de aquí la insinuación de que es provechoso estar en condiciones de variar entre representaciones procedimentales y declarativas. Probablemente, esto también sea correcto para IA.
Este problema fue puesto de relieve por Francis Crick, en una exposición sobre comunicación con inteligencias extraterrestres:
En la tierra, vemos que hay dos moléculas, una de las cuales es apta para la replicación [ADN] y la otra para la acción [proteínas]. ¿Es posible idear un sistema donde una molécula realice ambas tareas, o hay quizá poderosos argumentos, provistos por el análisis de sistemas, según los cuales (si es que existen) la división de la tarea en dos otorga una gran ventaja? No conozco la respuesta a esta interrogación.[14]
Otra de las cuestiones que aparecen en la representación del conocimiento es la modularidad. ¿Hasta qué punto es fácil insertar nuevos conocimientos? ¿Hasta qué punto es fácil revisar los conocimientos anteriores? ¿Hasta qué punto son modulares los libros? Todo depende. Si se extrae un solo capítulo de un libro trabadamente estructurado, pleno de referencias entrecruzadas, el resto del libro puede llegar a ser virtualmente incomprensible. Es como querer sacar un solo hilo de una telaraña: quien (o pretenda, arruinará el conjunto. Por otro lado, existen libros enteramente modulares, cuyos capítulos son independientes.
Examinemos un nada complicado programa de generación de teoremas, que utiliza axiomas y reglas de inferencia de TNT. El “conocimiento” de tal programa tiene dos aspectos: reside implícitamente en los axiomas y en las reglas, y explícitamente en el cuerpo de teoremas producidos hasta el momento de que se trate. Según el modo en que sea observado, el conocimiento será visto como modular, o como enteramente diseminado y, fuera de duda, no modular. Supongamos, por ejemplo, que hemos formulado un programa semejante pero nos hemos olvidado de incluir el Axioma 1 de TNT en la lista de axiomas. Después que el programas ya ha hecho varios miles de derivaciones, advertimos la omisión e insertamos el axioma faltante. El hecho de que podamos proceder de este modo, en un simple instante, muestra que el conocimiento implícito del sistema es modular; sin embargo, la contribución del nuevo axioma al conocimiento explícito del sistema sólo se verá reflejada luego de un largo lapso: después de que sus efectos se “difundan” de modo manifiesto, lo mismo que el aroma de un perfume se va difundiendo en una habitación luego de romperse el frasco que lo contenía. En este sentido, el nuevo conocimiento requiere de cierto plazo para ser incorporado. Asimismo, si se desea volver atrás y sustituir al Axioma 1 por su negación, no es posible limitarse a efectuar solamente este cambio, sino que es necesario, también, suprimir todos los teoremas en cuya derivación estuvo involucrado el Axioma 1, Está claro que el conocimiento explícito del sistema no está tan cercano a la modularidad como el conocimiento implícito.
Sería útil que aprendiéramos a trasplantar modularmente el conocimiento. Enseñar francés a alguien, así, requería nada más que abrir su cabeza y operar de manera fija sobre sus estructuras neurales, y ya sabría hablar francés; por supuesto, esto no es más que una quimera.
Otro aspecto de la representación del conocimiento se asocia con la forma en que se desea utilizarlo. ¿Se entiende que las inferencias son extraídas cuando llegan las piezas de información? ¿Se deben efectuar analogías y comparaciones, permanentemente, entre la información nueva y la información anterior? En un programa de ajedrez, pongamos por caso, cuando se desea crear árboles de anticipación es preferible una representación que codifique las posiciones de tablero con un mínimo de redundancia, en lugar de una representación que repitas la información en diversas formas. Pero si se quiere que el programa “comprenda” una posición de tablero mediante la búsqueda de patrones y su comparación con los patrones conocidos, será más indicada la representación de la misma información, reiterada a través de formas diferentes.
Existen varias escuelas de pensamiento interesadas en la forma más adecuada de representar el conocimiento, y manipularlo. Una que ha conseguido gran influencia aboga por representaciones que utilicen notaciones formales similares a las de TNT, y conectivos y cuantificadores proposicionales. Las operaciones básicas en tales representaciones son, y no es sorprendente, formalizaciones de razonamientos deductivos. Las deducciones lógicas pueden ser viabilizadas mediante el empleo de reglas de inferencia análogas a alguna de las de TNT. Interrogar al sistema con respecto a alguna noción en particular establece un objetivo, bajo la forma de una cadena que ha de ser derivada; por ejemplo: “¿MUMON es un teorema?”. Entonces, los mecanismos automáticos de razonamiento se hacen cargo de la operación, en una forma orientada hacia un objetivo y usando para ello diversos métodos de reducción de problemas.
Pongamos como ejemplo el supuesto de que la proposición “Todas las aritméticas formales son incompletas” es conocida, y que al programa se le pregunta: “¿Los Principia Mathematica son incompletos?”. Examinando la lista de hechos conocidos —llamada frecuentemente base de datos—, el sistema puede advertir que si puede establecer que los Principia Mathematica son una aritmética formal, ello daría respuesta a la pregunta. Por lo tanto, la proposición “Los Principia Mathematica son una aritmética formal” sería implantada como subobjetivo, y pasaría a aplicarse la reducción del problema. Si así son halladas otras cosas que ayuden a establecer (o a refutar) el objetivo o el subobjetivo, se trabajaría en ellas, y así siguiendo, recursivamente. Este proceso ha recibido el nombre de encadenamiento hacia atrás, puesto que se inicia planteando su objetivo y hace su camino hacia atrás, presumiblemente en dirección a cosas que pueden ser ya conocidas. Si se hiciera una representación gráfica del objetivo principal, de los objetivos subsidiarios, de los subsubobjetivos, etc., aparecería una estructura con aspecto de árbol, ya que el objetivo principal puede comprender diferentes subobjetivos, cada uno de los cuales, a su vez, abarcan diversos subsubobjetivos, etc.
Tómese nota de que este método no cuenta con la garantía de resolver la pregunta, pues es posible que no haya forma de establecer, dentro del sistema, que los Principia Mathematica son una aritmética formal. Esto no implica, sin embargo, que el objetivo o el subobjetivo sean enunciados falsos, sino que, simplemente, no pueden ser derivados a través del conocimiento ordinariamente disponible por parte del sistema. Este puede dar salida impresa, en tal circunstancia, a la expresión “No lo sé” u otra similar. El hecho de que ciertas preguntas queden abiertas es análogo, naturalmente, al de la incompletitud que aqueja a determinados sistemas formales muy bien conocidos.
Este método proporciona un conocimiento deductivo del dominio representado, en virtud de que, a partir de hechos conocidos pueden ser extraídas conclusiones lógicas correctas. No obstante, carece de algo como la aptitud humana para distinguir similitudes y comparar situaciones: carece de lo que podría llamarse conocimiento analógico, un elemento central de la inteligencia humana. Esto no quiere decir que los procesos de pensamiento analógico no puedan ser aprisionados dentro de un molde semejante, sino que no se prestan naturalmente a ser constreñidos por esa clase de formalismo. En nuestros días, los sistemas de orientación lógica no son tan frecuentes como los de otros géneros, los cuales permiten la realización bastante natural de formas complejas de comparación.
Cuando se comprende que la representación del conocimiento es algo enteramente distinto a un simple almacenamiento de números, la idea de que “una computadora tiene una memoria de elefante” pasa a ser un mito muy fácil de derrumbar. Lo que está almacenado en la memoria no es, necesariamente, sinónimo de lo que un programa sabe porque, aun cuando una determinada pieza de conocimiento haya sido codificada en algún sitio en el interior de un sistema complejo, puede que no haya ningún procedimiento, regla u otro género de operador de datos que estén en condiciones de llegar a ella: puede ser inaccesible. En tal caso, es factible decir que esa pieza de conocimiento ha sido “olvidada”, ya que el acceso a la misma está temporaria o permanentemente perdido. Así, un programa de computadora puede “olvidar” algo en un nivel alto, y “recordarlo” en un nivel bajo. Ésta es otra distinción de niveles siempre recurrente, de la cual tal vez podamos aprender mucho a propósito de nosotros mismos. Cuando un ser humano incurre en un olvido, lo más probable es que ello signifique que se ha perdido un señalador de alto nivel, y no que la información haya sido suprimida o destruida. Esto esclarece la enorme importancia de seguirle la pista a las formas en las cuales almacenamos las experiencias adquiridas, pues nunca se sabe con antelación cuáles serán las circunstancias, o el ángulo exigido, bajo los cuales necesitaremos recuperar alguna parte de lo que tenemos almacenado.
La complejidad de la representación del conocimiento en la mente humana golpeó por vez primera a mi puertas en oportunidad de encontrarme trabajando en un programa destinado a generar oraciones inglesas “desde la nada”. Había elegido este proyecto por un motivo muy interesante; luego de escuchar por radio algunas muestras del llamado “haiku de computadora”, hubo algo en ellas que me impresionó profundamente. Había un fuerte elemento humorístico, y simultáneamente de misterio, en conseguir que una computadora generase algo que corrientemente es considerado una creación artística. Disfruté muchísimo del aspecto jocoso, y me sentí altamente estimulado por el misterio —la contradicción, inclusive— albergado en la programación de actos creativos. De modo que emprendí la tarea de formular un programa aún más misteriosamente contradictorio y festivo que el programas haiku.
En un comienzo, me preocupé por flexibilizar y otorgar recursividad a la gramática, a fin de evitar la sensación de que el programa consistía sencillamente en un llenado de los espacios en blanco de una fórmula. Por ese tiempo tropecé con un artículo de Víctor Yngve, aparecido en Scientific American, donde describía una gramática simple, pero flexible, capaz de producir una amplia variedad del tipo de oraciones que figuran en algunos libros infantiles. Modifiqué algunas de las ideas que había encontrado en el artículo y elaboré un conjunto de procedimientos que integraban una gramática de la forma Red de Transición Recursiva, tal como es descrita en el Capítulo V. En esta gramática, la selección de palabras de una oración era determinada por un proceso que comenzaba por elegir —al azar— la estructura global de la oración; gradualmente, el proceso de adopción de decisiones se infiltraba a través de los niveles de estructura más bajos hasta alcanzar el nivel de la palabra y el de la letra. Por debajo del nivel de la palabra, había un montón de trabajo por hacer, como dar inflexión a los verbos, por ejemplo, o pluralizar sustantivos; los verbos irregulares y las formas nominales recibieron primero forma regular y después, si coincidían con las entradas de una tabla, se los sustituía por la forma adecuada (irregular). Al alcanzar su forma final, cada palabra recibía impresión de salida. El programa se parecía al proverbial mono que aprieta las teclas de una máquina de escribir, pero, a diferencia de esta situación, aquí la operación se cumplía sobre diversos niveles de la estructura lingüística, simultáneamente, y no sólo sobre el nivel de las letras. En las primeras etapas de desarrollo del programa, utilicé un léxico totalmente limitado: su forma deliberada, pues mi propósito era humorístico. Ello produjo una cantidad de oraciones sin sentido, algunas de las cuales tenían estructuras muy complicadas, mientras que otras eran bastante breves. A continuación, pueden apreciarse algunos ejemplos.
El efecto es fuertemente surrealista y por momentos recuerda un poco al del haiku, como por ejemplo la pauta que siguen las cuatro oraciones consecutivas del final. Al principio, esto resultó muy divertido y tuvo su encanto, pero pronto se convirtió en algo trillado; luego de leer unas pocas páginas de salida podían percibirse los límites del espacio dentro del cual estaba operando el programa; después de eso, la observación de puntos elegidos al azar en el interior de tal espacio —aunque se tratase de cosas “nuevas”— no daba la impresión de estar viendo nada nuevo. Hay aquí, según creo, un principio general: uno se aburre de algo, no cuando agotó su repertorio de conducta, sino cuando tiene delineados los límites del espacio que contiene a la conducta. El espacio de comportamiento de una persona es, prácticamente, lo suficientemente complejo como para que pueda seguir sorprendiendo a los demás; pero no ocurrió así con mi programa. Comprendí que mi finalidad de obtener resultados verdaderamente cómicos requería la programación de una sutileza mucho mayor. Pero, en ese caso, ¿qué significaba “sutileza”? Estaba claro que la sola yuxtaposición absurda de palabras no era demasiado sutil; yo necesitaba un medio para asegurar que las palabras fuesen empleadas con arreglo a las realidades de este mundo. Fue entonces cuando ingresaron a la escena las reflexiones sobre la representación del conocimiento.
El criterio que adopté consistió en clasificar cada palabra —sustantivo, verbo, preposición, etc.— en diversas “dimensiones semánticas” diferentes. Así, cada palabra pertenecía a alguna de entre varías clases; había después, también, superclases: clases de clases (lo cual recuerda las observaciones de Ulam). En principio, tal agregación podría continuarse a través de cualquier cantidad de niveles, pero yo me detuve en el segundo. En todo momento, la elección de palabras, ahora, estaba semánticamente restringida, porque se requería que existiese acuerdo entre las diversas partes de la expresión que estaba siendo construida. Por ejemplo, la idea consistía en que ciertas clases de actos pudiesen ser realizados únicamente por objetos animados, o que sólo ciertos tipos de abstracción pudiesen ejercer influencia sobre los acontecimientos, etc. Las decisiones relativas a qué categorías eran las adecuadas, y a si era mejor considerar a cada categoría como clase o como superclase, eran sumamente complicadas. Todas las palabras estaban discriminadas en varias dimensiones diferentes. Las preposiciones comunes —“de”, “en”, etc.— tenían varías entradas distintas, correspondientes a sus distintos usos. La salida, ahora, comenzó a ser mucho más comprensible, y eso la hizo divertida en otro sentido.
Más abajo, reproduzco nueve selecciones, cuidadosamente entresacadas de muchas páginas de salida correspondientes a las últimas versiones de mi programa. Junto con ellas, he incluido tres oraciones (seriamente pensadas) de proveniencia humana, ¿cuales son?
Según los sofistas, las campañas en las ciudades estados, en otras palabras, habían sido aceptadas por el Oriente hábilmente. Por supuesto, el Oriente ha sido dividido por los estados muy violentamente.
El Oriente apoya los esfuerzos que han sido apoyados por la humanidad.
Las oraciones formuladas por seres humanos son las tres primeras; fueron extraídas de un número reciente de la revista Art-Language[15] y son —hasta donde yo puedo afirmarlo— intentos totalmente serios, elaborados por personas letradas y sensatas, de comunicarse entre sí determinadas cosas. El hecho de que aparezcan aquí fuera de su contexto no contribuye demasiado a dificultar la interpretación, pues dicho contexto suena exactamente igual que las oraciones citadas.
El resto fue producido por mi programa. Las números 10 a 12 fueron elegidas para mostrar que hubo, ocasionalmente, arranques de absoluta lucidez; los números 7 a 9 son más representativas de la salida: flotan en ese extraño y provocativo inframundo ubicado entre la significación y la no significación; y luego, las números 4 a 6 están casi más allá de la significación. Generosamente, se podría decir que conciernen a sí mismas en tanto que “objetos de lenguaje” puros, algo semejante a segmentos de escultura abstracta hechos, no de piedra, sino de palabras; como alternativa, se podría decir que son pura cháchara seudointelectual.
A pesar de ello, mi elección del vocabulario estuvo dirigida a producir efectos humorísticos. El tono de la salida es difícil de caracterizar. Si bien una gran proporción de la misma “tiene sentido”, al menos en el nivel de la oración individual, se extrae la impresión terminante de que la salida está brotando de una fuente que carece a toda comprensión de lo que está diciendo, y de todo motivo para decirlo. En particular, se siente una absoluta falta de imaginación visual por detrás de las palabras. Al ver aparecer estas oraciones en la línea impresora, experimenté emociones complejas. Yo estaba muy divertido con lo disparatado de la salida, y también sumamente orgullosos de mi logro, y trataba de describirlo a mis amigos como similar a la fijación de reglas para la elaboración de parábolas, en árabe, mediante pinceladas individuales: una exageración, pero me complacía verlo de tal modo. Por último, estaba profundamente conmovido por el conocimiento que esta máquina enormemente complicada estaba haciendo fluir a lo largo de extensas hileras de símbolos ubicados en su interior, con sujeción a determinadas reglas, y que estas extensas hileras de símbolos eran algo parecido a los pensamientos de mi propia cabeza… algo parecido.
Por supuesto, no me dejé llevar por la fantasía de que hubiera un ser consciente detrás de las oraciones; lejos de ello, yo era la persona que mejor sabía en el mundo las razones por las cuales este programas se encontraba terriblemente alejado del pensamiento real. El Teorema de Tesler viene muy a propósito en este instante: tan pronto como ese nivel de capacidad de manipulación idiomática hubo sido mecanizado, quedó en claro que no constituía inteligencia. Pero esta intensa experiencia me proveyó una imagen: la vislumbrada sensación de que el pensamiento real está compuesto por hileras de símbolos, en el cerebro, mucho más extensas y mucho más complicadas… muchas hileras como trenes desplazándose simultáneamente sobre rieles paralelos y entrecruzados, con sus vagones empujados y arrastrados, enganchados y desenganchados, desplazados de una vía a otra por una miríada de mecanismos guardagujas neurales…
Se trataba de una imagen intangible que no puedo transmitir en palabras, y no era más que una imagen. Pero imágenes e intuiciones y motivaciones reposan entremezcladas en la mente, y mi estado de concentrada fascinación frente a esta imagen era un acicate constante para reflexionar más profundamente sobre qué puede ser realmente el pensamiento. En otras partes de este libro he tratado de comunicar algunas imágenes, hijas de esta imagen original, particularmente en el Preludio y Furmiga…
Lo que permanece ahora en mi mente, cuando examino este programa doce años más tarde, es la inexistencia de todo sentido imaginativo por detrás de lo que se estaba diciendo. El programa no tenía idea de lo que es un siervo, de lo que es una persona, ni de lo que es cosa alguna en absoluto. Las palabras eran símbolos formales vacíos, tan vacíos como —o quizá más todavía— la m y la g del sistema mg. Mi programa se benefició con el hecho de que, cuando la gente lee un texto, tiende en forma enteramente natural a incorporar a cada palabra todas sus resonancias, como si estuviesen forzosamente adscriptas al grupo de letras que forman la palabra. Mi programa puede ser visto como un sistema formal, cuyos “teoremas” —las oraciones de salida— tuviesen interpretaciones ya listas (al menos, para los hablantes de inglés). A diferencia del sistema mg, empero, estos “teoremas” no resultaban por entero enunciados verdaderos al ser interpretados de tal forma. Muchos eran falsos, muchos eran sinsentidos.
En su humilde medida, el sistema mg refleja un diminuto rincón del mundo. Pero el procesamiento de mi programa no arroja reflejo alguno de cómo funciona el mundo, a excepción de las pequeñas construcciones semánticas a las cuales debe sujetarse. Para crear tal reflejo de comprensión, yo debería haber envuelto cada concepto en capas y más capas de conocimiento del mundo. Proceder así hubiera constituido una clase de esfuerzo diferente al que me propuse. No es que no haya pensado, frecuentemente, en intentarlo, sino que nunca anuncié la decisión de hacerlo.
En realidad, he evaluado a menudo la posibilidad de formular una gramática RTA (o alguna otra índole de programa productor de oraciones) destinada a producir únicamente oraciones verdaderas acerca del mundo. Tal gramática incorporaría palabras con significaciones auténticas, tal como sucede en el sistema mg y en TNT. Esta idea de un lenguaje donde los enunciados falsos sean no gramaticales es antigua: fue imaginada por Johann Amos Comenius, en 1633. Es muy atractiva porque la gramática pasa a contar con una bola de cristal en su seno: uno se limita a formular el enunciado que le interesa, y verifica si es gramatical… Realmente, Comenius fue aún más allá, pues en su lenguaje los enunciados falsos no sólo eran no gramaticales, ¡sino también inexpresables!
Orientando este pensamiento en otra dirección, es posible imaginar una gramática de alto nivel que produzca kōans fortuitos. Y, si se tuviera un programa así, ¿se lo podría disponer para que produzca exclusivamente kōans auténticos? Mi amiga Marsha Meredith se entusiasmó con este proyecto de “Ismo Artificial”, y tomó la iniciativa de elaborar un programa de enunciación de kōans. Uno de sus primeros esfuerzos dio lugar a este curioso cuasi kōan:
UN PEQUEÑO MAESTRO JOVEN DESEABA UN PEQUEÑO CUENCO BLANCO DE MADERA. “¿CÓMO PODEMOS APRENDER Y COMPRENDER SIN ESTUDIAR?”. PREGUNTÓ EL JOVEN MAESTRO A UN CONFUNDIDO MAESTRO GRANDE. EL CONFUNDIDO MAESTRO CAMINÓ DESDE UNA ABRUPTA MONTAÑA PARDA HASTA UNA APACIBLE MONTAÑA BLANCA CON UN PEQUEÑO CUENCO ROJO DE PIEDRA. EL CONFUNDIDO MAESTRO VIO UNA APACIBLE CABAÑA ROJA. EL CONFUNDIDO MAESTRO DESEABA LA CABAÑA. “¿POR QUÉ FUE BODHIDHARMA A CHINA?”. PREGUNTÓ EL CONFUNDIDO MAESTRO A UN DISCÍPULO ILUMINADO GRANDE. “LOS MELOCOTONES SON GRANDES”, RESPONDIÓ EL DISCÍPULO AL CONFUNDIDO MAESTRO. “¿CÓMO PODEMOS APRENDER Y COMPRENDER SIN ESTUDIAR?”. PREGUNTÓ EL CONFUNDIDO MAESTRO A UN ANCIANO MAESTRO GRANDE. EL ANCIANO MAESTRO CAMINÓ DESDE UNA BLANCA G0025 DE PIEDRA. EL ANCIANO MAESTRO SE PERDIÓ.
Es probable que el procedimiento personal de decisión del lector logre un veredicto acerca de la autenticidad de este kōan, sin necesidad de apelar al Código Geométrico del Arte de los Cordones Zen. Si la ausencia de pronombres o la simplificada sintaxis no le sugiere ninguna sospecha, seguramente sí lo hará ese extraño “G0025” cercano al final. ¿Qué es eso? Una rara casualidad; la manifestación de un error, el cual dio lugar a que el programa imprimiera, en lugar de una palabra idiomática referida a un objeto, el número interno asignado en el programa al “nódulo” (un átomo Lisp, en realidad) donde estaba almacenada toda la información concerniente a ese objeto específico. De modo que tenemos aquí una “ventana” abierta sobre un nivel inferior de los fundamentos de la mente zen, un nivel que debería haber permanecido invisible. Lamentablemente, no contamos con semejantes ventanas que transparenten los niveles inferiores de las mentes zen humanas.
La secuencia de acciones, aunque un tanto caprichosa, se deriva de un procedimiento recursivo Lisp, denominado “CASCADA”, el cual genera cadenas de acciones asociadas entre sí en forma vagamente causal. Pese a que el grado de comprensión del mundo mostrado por este productor de kōans no es, sin duda, estupendo, continúan los esfuerzos a fin de conseguir salidas de aspecto algo más auténtico.

FIGURA 116. Una parábola en árabe. [Tomado de: A. Khatibi y M. Sijelmassi, The Splendour of Islamic Calligraphy (New York: Rizzoli, 1976).]
Tenemos luego la música. Se trata de un dominio del cual se puede suponer, en una primera consideración, que se prestaría admirablemente a ser codificado en una gramática RTA, o en otro programa. Al tiempo que (para avanzar en esta línea ingenua de pensamiento) el lenguaje depende de conexiones con el mundo exterior para asumir significación, la música es puramente formal. No hay referencia a cosas de “allí fuera” en los sonidos musicales; éstos no son sino solamente una sintaxis, las notas siguen a las notas, los acordes a los acordes, los compases a los compases, las frases a las frases…
Pero, un momento. Hay algo que no está bien en este análisis. ¿Por qué hay música que es mucho más profunda y más bella que otra? Porque la forma, en música, es expresiva, expresiva de algunas extrañas regiones subconscientes de nuestras mentes. Los sonidos musicales no se refieren a siervos o a ciudades estados, pero desencadenan enjambres de emociones en nuestra más profunda interioridad; en este sentido, la significación musical es dependiente de intangibles lazos entre los símbolos y las cosas de este mundo: “cosas” que, en este caso, son secretas estructuras software de la mente. No, la gran música no surgirá de un formalismo tan sencillo como una gramática RTA. Sí puede surgir seudomúsica, lo mismo que seudocuentos de hadas —y se tratará de una exploración valiosa por parte de quienes la efectúen—, pero los secretos de la significación musical reposan en un sitio muchísimo más profundo que la pura sintaxis.
Aquí, debo aclarar una cuestión: en principio, las gramáticas RTA tienen la misma potencialidad que cualquier formalismo de programación, de modo que si la significación es, de alguna manera (yo así lo creo), capturable, puede ser capturada por una gramática RTA. Verdaderamente. A pesar de eso, sostengo que, en tal caso, la gramática habrá de definir no solamente estructuras musicales, sino las estructuras íntegras de la mente del espectador. La “gramática” será una gramática total del pensamiento y no, exclusivamente, una gramática de la música.
¿Qué clase de programa conseguiría que los seres humanos, aun con reticencia, admitiesen que está dotado de “compresión”? ¿Qué es lo que nos llevaría primero a aceptar que no sentimos intuitivamente que allí “no hay nada”?
Entre los años 1968 y 1970, Terry Winograd (alias Dr. Rony W. Tigera) estudiaba el doctorado en el Instituto Tecnológico de Massachusetts, donde trabajó conjuntamente en problemas de lenguaje y de comprensión. Allí, por ese entonces, gran parte de la investigación en IA estaba dedicada a los llamados mundos de bloques, un dominio relativamente simple, donde los problemas relativos al manejo simultáneo del lenguaje y de la visión por las computadoras podían coordinarse con facilidad. Un mundo de bloques consiste en diversas clases de bloques parecidos a los de juguete, ubicados sobre una mesa; los bloques son de distintos colores, y su forma es cuadrada, oblonga, triangular, etc. (Un “mundo de bloques” de otro género lo encontramos en la figura 117, que reproduce la obra de Magritte, Aritmética mental. Creo que este título es singularmente adecuado con respecto al presente contexto). Los problemas visuales en los bloques del 1TM son sumamente complicados: ¿cómo puede descubrir una computadora, mediante un vistazo a una escena de televisión que muestra muchos bloques, exactamente qué clases de éstos hay, y cómo se relacionan entre sí? Algunos bloques pueden estar montados sobre otros, o en cambio estar enfrentados, es posible que haya sombras, etc.

FIGURA 117. Aritmética mental, de René Magritte (1931).
La actividad de Winograd estuvo apartada de los problemas de visión. Partiendo de la suposición de que los bloques se encontraban bien representados dentro de la memoria de la computadora, hizo frente al multifacético problema de cómo obtener que la computadora:
Parecería razonable fragmentar el programa global en subprogramas modulares, con un módulo para cada parte diferente del problema; y después, una vez desarrollados los módulos por separado, integrarlos con toda tranquilidad. Winograd halló que tal estrategia de desarrollo independiente de los módulos planteaba dificultades fundamentales. Lo que formuló fue un enfoque radical, que desafiaba la teoría de que la inteligencia puede ser compartimentada en piezas independientes o semiindependientes. Su programa SHRDLU —que recibió su nombre del antiguo código “ETAOIN SHRDLU”, usado por los linotipistas para indicar los errores tipográficos en las columnas de los periódicos— no separa los problemas en nítidas partes conceptuales. Las operaciones de análisis de oraciones, de producción de representaciones internas, de razonamientos acerca del mundo representado en su interior, de evacuación de preguntas, etc., se encuentran profunda e intrincadamente entrelazadas en una representación procedimental del conocimiento. Algunos críticos han señalado que este programa está tan entremezclado que no representa para nada una “teoría” sobre el lenguaje, ni contribuye de ninguna manera a profundizar nuestro conocimiento de los procesos del pensamiento. Nada más erróneo que estas impugnaciones, en mi opinión. Un tour de forcé tal como SHRDLU quizá no sea isomórfico de los procesos humanos —por cierto, no se puede pensar, en absoluto, que en SHRDLU haya sido alcanzado el “nivel simbólico”— pero el hecho de crearlo y de pensar en sus alcances permite una penetración enorme en las formas en que actúa la inteligencia.
En realidad, SHRDLU consiste en procedimientos separados, cada uno de los cuales contiene cierto conocimiento acerca del mundo; sin embargo, los procedimientos tienen una interdependencia tan poderosa que no pueden ser mantenidos en forma prolijamente separada. El programa es como un nudo fuertemente amarrado que se resiste a ser desatado, pero el hecho de no poder desanudarlo no quiere decir que no se pueda comprenderlo. Puede haber una rigurosa descripción geométrica del nudo entero aun cuando éste sea físicamente desordenado; tal vez convenga recordar una metáfora de la Ofrenda Mu, la de la observación de un huerto desde un ángulo “natural”, y compararla con esta situación.
Winograd ha escrito lúcidamente a propósito de SHRDLU. La cita que sigue corresponde a su artículo en el libro de Schank y Colby:
Uno de los puntos de vista básicos que subyacen al modelo, es que todo uso del lenguaje puede ser considerado como una forma de activación de procedimientos en el interior del oyente. Podemos considerar cualquier enunciación como un programa: un programa que genera, indirectamente, un conjunto de operaciones que deben ser cumplidas dentro del sistema cognoscitivo del oyente. Esta “formulación de programa” es indirecta, en el sentido de que estamos tratando con un intérprete inteligente, quien puede emprender un conjunto de acciones que son totalmente diferentes de las concebidas por el hablante. La forma exacta es determinada por su conocimiento del mundo, sus expectativas en relación con la persona que le habla, etc. En este programa, tenemos una versión simple de ese proceso de interpretación, tal como tiene lugar en el robot. Cada oración interpretada por el robot es convertida en un conjunto de instrucciones en PLANNER. El programa que resulta es entonces ejecutado, a fin de obtener los efectos buscados.[16]
El lenguaje PLANNER, recién mencionado, es un lenguaje IA cuyo rasgo principal es que algunas de las operaciones necesarias para la reducción del problema están incorporadas en él, operaciones como por ejemplo el proceso recursivo de generación de un árbol de subobjetivos, subsubobjetivos, etc. Esto significa que tales procesos, en lugar de tener que ser estudiados una y otra vez por el programador, están implicados automáticamente en los llamados enunciados OBJETIVO. Cualquiera que lea un programa PLANNER no verá ninguna referencia explícita a tales operaciones; en jerga técnica, se las denomina transparentes al usuario. Si un recorrido del árbol no consigue obtener el fin buscado, el programa PLANNER “retornar” e intentará otra ruta. En todo lo concerniente a PLANNER, la palabra mágica es “retorno”.
El programa de Winograd hizo excelente empleo de estos aspectos de PLANNER o, más exactamente, de MICROPLANNER, una instrumentación parcial de los diseños de PLANNER. En los últimos años, sin embargo, personas interesadas en el desarrollo de IA han llegado a la conclusión de que el retorno automático, como el de PLANNER, es definitivamente desventajoso, y que probablemente no sea útil para avanzar en ese desarrollo; en consecuencia, han desistido de aquel recurso y optado por retornar a ensayar otros caminos.
Oigamos otros comentarios de Winograd sobre SHRDLU:
La definición de cada palabra es un programa al cual se apela en un punto adecuado del análisis, y que puede efectuar computaciones discrecionales que abarquen la oración y la situación física presente.[17]
Éste es uno de los ejemplos citados por Winograd:
Las diferentes posibilidades de significación de “el” son procedimientos que verifican diversos hechos referentes al contexto, y luego prescriben acciones tales como “Buscar un objeto único en la base de datos que se ajuste a esta descripción”, o “Afirmar que el objeto bajo descripción es único en lo que toca al hablante”. El programa tiene incorporada una variedad de recursos heurísticos para decidir qué parte del contexto es pertinente.[18]
Es asombrosa la profundidad de este problema vinculado a la palabra “el”. Tal vez no haga falta decir que la formulación de un programa que pueda manejar en plenitud las cinco palabras cumbre de un idioma —en español, “de”, “el”, “la”, “y” y “a”— equivaldría a la resolución de todo el problema de IA, e implicaría, entonces, conocer qué son la inteligencia y la conciencia. Una pequeña digresión: los cinco sustantivos más comunes, en español, son “hombre”, “vida”, “vez”, “día” y “don” (en ese orden), según el Frequency Dictionary of Spanish Words de Juillard y Chang-Rodríguez (Mouton, The Hague, 1964). Lo llamativo, aparte del increíble “don” en quinta posición, es que la mayor parte de la gente no tiene idea de que pensamos en términos tan abstractos. Si preguntamos a nuestros amigos, diez a uno que supondrán que las palabras más usadas son “casa”, “auto”, “perro”, “dinero”… Y —ya que estamos en el tema de las frecuencias— las doce letras de empleo cumbre en inglés son, de acuerdo a Mergenthaler: “ETAOIN SHRDLU”.
Un aspecto gracioso de SHRDLU es que se opone totalmente al estereotipo de las computadoras como “masticadoras de números” ya que, en palabras de Winograd: “Nuestro sistema no acepta los números bajo forma numérica, y se le ha enseñado a contar solamente hasta diez”.[19] ¡Con toda la matemática que lo apuntala, SHRDLU apenas sabe contar! Exactamente igual que Codogne Madame d’Or Migas, SHRDLU no sabe nada con respecto a los niveles más bajos que lo constituyen; su conocimiento es, en su mayor medida, procedimental (véase, particularmente, la observación que hace el “Dr. Rony W. Tigera” en el paso 11 del diálogo precedente).
Es interesante comparar la incorporación procedimental de conocimiento en SHRDLU con el conocimiento de mi programa generador de oraciones. Todo el conocimiento sintáctico de mi programa fue incorporado procedimentalmente en Redes de Transición Aumentada, formuladas en lenguaje Algol; sin embargo, el conocimiento semántico —la información sobre los miembros de las clases semánticas— era estático: estaba contenido en una breve lista de números subsiguiente a cada palabra. Había unas pocas palabras, como los verbos auxiliares “ser”, “haber” y otros, representadas totalmente mediante procedimientos de Algol, pero se trató de excepciones. Por el contrario, en SHRDLU, todas las palabras se representaron como programas. Este ejemplo demuestra que a pesar de la equivalencia teórica de datos y programa, la elección de unos en lugar de otros tiene, en la práctica, consecuencias principales.
FIGURA 118. Representación procedimental de “un cubo rojo que sostiene a una pirámide”. [Adaptado de: Roger Schank y Kenneth Colby, Computer Models of Thought and Language (San Francisco: W. H. Freeman, 1973), p. 172.]
Ahora, algunas otras palabras de Winograd:
Nuestro programa no opera analizando, en primer lugar, una oración, haciendo luego análisis semántico, para terminar utilizando la deducción a fin de producir una respuesta. Estas tres actividades se presentan concurrentemente a todo lo largo de la comprensión de una oración. Ni bien comienza a tomar forma una pieza de estructura sintáctica, se apela a un programa semántico para que vea si tiene sentido, y la respuesta resultante puede dirigir el análisis. Para decidir si existe sentido, la rutina semántica puede apelar a procesos deductivos y formular preguntas acerca del mundo real. Por ejemplo, frente a la oración 34 del diálogo (“pon la pirámide azul sobre el bloque en la caja”), el analizador toma “la pirámide azul sobre el bloque” como posible grupo nominal. En este punto, es efectuado el análisis semántico, y después de ser definida “la”, tiene lugar una verificación en la base de datos con respecto al objeto aludido. Si tal objeto no es encontrado, el análisis es redirigido para que encuentre el grupo nominal “la pirámide azul”. Después, continuará con la ubicación de “sobre el bloque en la caja” como una expresión individual que indica localización… De este modo, hay una interrelación continua entre los diferentes géneros de análisis, con el resultado de que cada uno afecta a los restantes.[20]
Es interesante el hecho de que, en los lenguajes naturales, la sintaxis y la semántica estén así profundamente imbricadas. En el capítulo anterior, cuando abordamos el elusivo concepto de “forma”, lo separamos en dos categorías: forma sintáctica, detectable mediante un procedimiento de decisión de finalización predictible, y forma semántica, la cual no es detectable de esa manera. Pero aquí, Winograd no está diciendo que —al menos cuando se habla de “sintaxis” y “semántica” en el sentido usual— ambas se presentan directamente fusionadas en el lenguaje natural. La forma externa de una oración —esto es, su composición en términos de signos elementales— no permite una separación neta entre aspectos sintácticos y semánticos. Ésta es una cuestión muy significativa para la lingüística.
Algunos comentarios finales sobre SHRDLU, por parte de Winograd:
Observemos lo que haría el sistema con una descripción simple como “un cubo rojo que sostiene a una pirámide”. La descripción utilizará conceptos como BLOQUE, ROJO, PIRÁMIDE y EQUIDIMENSIONAL, partes, todos ellos, de la categorización subyacente del mundo por parte del sistema El resultado puede ser representado en un organigrama como el de la figura 118. Adviértase que éste es un programa destinado a encontrar un objeto que se ajuste a la descripción. Luego, sería incorporada una orden para que se haga algo con ese objeto, una pregunta acerca del mismo o, si aparece en un enunciado, se convertiría en parte del programa que ha sido generado para representar la significación, con vistas a su uso posterior. Adviértase que este fragmento de programa también puede utilizarse como verificación de si un objeto se ajusta a la descripción, en el caso de que la primera indicación ENCUENTRA se emitiese con anterioridad al examen exclusivo de ese objeto particular.
A primera vista, da la impresión de que este programa tiene demasiada estructura, en la medida en que no queramos pensar que la significación de una simple expresión contiene, en forma explícita, bucles, verificaciones condicionales y otros detalles de programación. La solución reside en proporcionar un lenguaje interno que contenga los bucles y verificaciones propios de sus originales, y donde la representación del proceso sea tan simple como la descripción. El programas que se describe en la figura 118, formulado en PLANNER, tendría esta apariencia:
(OBJETIVO (ES ?XI BLOQUE))
(OBJETIVO (COLOR DE ?XI ROJO))
(OBJETIVO (EQUIDIMENSIONAL ?XI))
(OBJETIVO (ES ?X2 PIRÁMIDE))
(OBJETIVO (SOSTIENE A ?XI ?X2))
Los bucles del organigrama están implícitos en la estructura de control de retomo de PLANNER. La descripción es evaluada mediante el seguimiento de la lista hasta que fracasa algún objetivo, instante en el cual el sistema retorna automáticamente al último punto donde fue adoptada una decisión, e intenta otra posibilidad. Se puede adoptar una decisión dondequiera que aparezca un nuevo nombre de objeto o VARIABLE (señalada por el prefijo “?”), como “?X1” o “?X2”. Las variables son utilizadas por el comparador de patrones. Si ya han sido asignadas a un ítem particular, este último verifica si el OBJETIVO es verdadero para ese ítem. Si no es así, verifica la existencia de todos los ítems que puedan satisfacer el OBJETIVO, mediante la elección de uno de ellos, y luego de otros sucesivamente, en todo punto hasta el cual se produzca el retomo. Así, la distinción entre elección y verificación, inclusive, es implícita.[21]
Una importante decisión estratégica, en el diseño de este programa, fue la de no hacer una traducción total del inglés a Lisp, sino solamente parcial, y a PLANNER. De esta forma (puesto que el intérprete PLANNER es, por su parte, formulado en Lisp), fue insertado un nuevo nivel intermedio —PLANNER— entre el lenguaje de nivel máximo (inglés) y el lenguaje de nivel mínimo (lenguaje de máquina). Una vez elaborado un programa PLANNER a partir de un fragmento de oración inglesa, puede ser remitido al intérprete PLANNER, y entonces los niveles superiores de SHRDLU quedan en libertad de ocuparse de otras tareas.
La clase de decisión que se plantea constantemente es: ¿cuántos niveles debe tener un sistema? ¿Cuánta, y de qué tipo, ha de ser la “ingeligencia” colocada en cada nivel? Éstos son algunos de los problemas arduos que enfrenta IA en la actualidad. A causa de que es muy poco lo que sabemos de la inteligencia natural, no es difícil determinar qué nivel de un sistema artificialmente inteligente tiene que ejecutar tal parte de una tarea.
Esto permite contar con una visión de lo que hay detrás de las escenas del diálogo precedente. En el próximo capítulo, entraremos en contacto con nuevas y especulativas ideas en materia de IA.