CAPÍTULO XVII

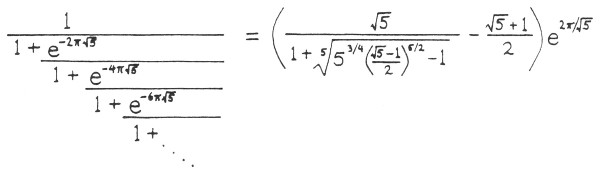
Church, Turing, Tarski y otros

Sistemas formales e informales

HEMOS LLEGADO AL momento en que podemos desarrollar una de las tesis principales de este libro: la de que todos los aspectos del pensamiento pueden ser vistos como una descripción de alto nivel de un sistema que, en un bajo nivel, es gobernado por reglas simples e, inclusive, formales. El “sistema”, por supuesto, es el cerebro, a menos que se esté hablando de procesos de pensamiento circulantes en otro medio, como por ejemplo los circuitos de una computadora. La imagen es la de un sistema formal subyacente a un “sistema informal”; un sistema que, digamos, elabore juegos de palabras, descubra patrones numéricos, olvide nombres, cometa disparates imperdonables jugando al ajedrez, etc. Ésta es la visión desde el exterior: su manifiesto e informal nivel software. En contraste, el sistema tiene un oculto y formal nivel hardware (o “sustrato”), el cual consiste en un mecanismo formidablemente complejo que efectúa las transiciones entre estado y estado, con arreglo a reglas definidas, físicamente incorporadas a aquél, y con arreglo también a la entrada de las señales con las que tropieza.

No hace falta recordar que semejante manera de considerar el cerebro tiene muchas implicaciones filosóficas, y de otra índole. Trataré de detallar algunas de ellas en este capítulo. Entre otras cosas, esta perspectiva parece dar por sentado que, en el fondo, el cerebro es una suerte de objeto “matemático”. En rigor, ésta es, en el mejor de los casos, una manera muy inadecuada de analizar el cerebro, porque, aun cuando éste fuese, en un sentido técnico y abstracto, una suerte de sistema formal, seguiría siendo cierto que los matemáticos operan exclusivamente con sistemas simples y precisos, donde todo es definido de modo extremadamente claro; el cerebro, en tanto, está a enorme distancias de una situación así, con sus diez mil millones, o todavía más, de neuronas semindependientes, conectadas casi caprichosamente entre sí. De modo pues, que los matemáticos no tomarían como objeto de estudio las redes de un cerebro real. Y si la “matemática” es definida como aquello que los matemáticos disfrutan ejercitando, las propiedades del cerebro no son entonces matemáticas.

La única posibilidad de comprender un sistema de complejidad del cerebro radica en una articulación en bloques que diferencie niveles más y más altos, con la consecuencia de ver sacrificada cierta dosis de precisión en cada paso. Lo que emerge en el nivel superior es el “sistema informal”, el cual obedece a incontables reglas de semejante complejidad, que aún no contamos con un léxico para pensar en ello. Esto es lo que la investigación en materia de Inteligencia Artificial espera descubrir, y se trata de algo cuyo tono difiere por completo de la investigación matemática.

Con todo, existe una conexión, laxa, con la matemática: a menudo, los investigadores de IA están dotados de una sólida formación matemática, y los matemáticos pueden sentirse intrigados por el funcionamiento de su propio cerebro. El pasaje que sigue, extraído de Adventures of a Mathematician, obra autobiográfica de Stanislaw Ulam, ilustra este rasgo:

La intuición y el magnífico Cangrejo

Como se acaba de señalar, comúnmente se hace referencia a la Inteligencia Artificial mediante las siglas “IA”. Con frecuencia, cuando trato de explicar qué quiere decir esta expresión, digo que las letras “IA” podrían representar muy bien, asimismo, a “Intuición Artificial” o, inclusive, a “Imaginación Artificial”. El objetivo de IA es averiguar qué sucede cuando la mente, silenciosa e invisiblemente, elige, de entre una miríada de alternativas, la que tiene mayor sentido para ser aplicada a una situación sumamente compleja. En muchas circunstancias de la vida real, el razonamiento deductivo es inadecuado, no porque brinde respuestas erróneas, sino porque pueden ser formulados muchísimos enunciados correctos pero no pertinentes; son demasiadas las cosas que se deben tomar en consideración simultáneamente, para que baste el solo razonamiento. Veamos este minidiálogo:

Se requiere —“¿qué tiene importancia aquí, y qué cosa no?”— un sentido del juicio y, ligado a éste, un sentido de la simplicidad y un sentido de la belleza. ¿De dónde provienen estas intuiciones? ¿Cómo pueden surgir de un sistema formal subyacente?

En el Magnificangrejo son puestas de manifiesto algunas facultades inusuales de la mente del Cangrejo. Su propia versión de las mismas consiste en la simple mención de que escucha una música y puede distinguir entre belleza y no belleza. (Por lo visto, él cree que existe al respecto una nítida línea divisoria). Pero Aquiles descubre otro medio para describir las aptitudes del Cangrejo: éste discrimina enunciados de teoría de los números en dos categorías, verdaderos y falsos. Ahora bien, el Cangrejo sostiene que si acertó a proceder así ha sido por mero accidente pues, según su propia confesión, es incompetente en materia de matemática. Lo que principalmente crea la perplejidad de Aquiles es que ese logro del Cangrejo, sin embargo, parece constituir una violación flagrante de una célebre conclusión metamatemática que a Aquiles le es familiar:

TEOREMA DE CHURCH: No hay método infalible que discrimine entre teoremas y no teoremas de TNT.

Esto fue demostrado en 1936 por el lógico estadunidense Alonzo Church. Se le relaciona estrechamente lo que yo llamo el

TEOREMA TARSKI-CHURCH-TURING: No hay método infalible que discrimine entre enunciados verdaderos y falsos de teoría de los números.

La Tesis Church-Turing

Para entender mejor el Teorema de Church y el Teorema Tarski-Church-Turing, tendríamos que comenzar por referirnos a una de las ideas sobre las cuales se basan; y ésta es la Tesis Church-Turing (llamada muchas veces “Tesis de Church”): la Tesis Church-Turing es, indudablemente, uno de los elementos conceptuales de mayor importancia en la filosofía de la matemática, del cerebro y del pensamiento.

En verdad, la Tesis Church-Turing, igual que el té, puede ser preparada de modo que salga más o menos fuerte, dentro de una variedad de posibilidades. Así es que la presentaré a través de diversas versiones, e iremos analizando el significado de cada una.

La primera versión suena muy inocente; en realidad, poco menos que obtusa:

TESIS CHURCH-TURING, VERSIÓN TAUTOLÓGICA: Los problemas matemáticos pueden ser resueltos únicamente mediante el ejercicio de la matemática.

Por supuesto, la significación, aquí, reposa en la significación de los términos constituyentes. Al decir “problemas matemáticos” aludo al problema de decidir si cierto número posee o no posee una propiedad aritmética determinada. Ocurre que, gracias a la numeración Gödel y a los recursos de codificación asociados con la misma, prácticamente ningún problema de ninguna rama de la matemática puede ser formulado de esta forma; de modo, pues, que “problemas matemáticos” conserva su significación ordinaria. ¿Qué pasa con “el ejercicio de la matemática”? Cuando uno intenta resolver si un número tiene cierta propiedad, parece haber solamente un reducido número de operaciones por emplear, combinadamente, repetidas veces: suma, multiplicación, verificación de igualdad o desigualdad. O sea que los bucles compuestos por tales operaciones, parece, son la única herramienta que permite explorar el mundo de los números. Repárese en la palabra “parece”: es la palabra crítica por la que se preocupa la Tesis Church-Turing. Podemos hacer una revisión:

TESIS CHURCH-TURING, VERSIÓN HABITUAL Supongamos que existe un método seguido por un ser consciente para distribuir los números en dos clases. Supongamos, asimismo, que este método produce siempre una respuesta dentro de un lapso finito, y que siempre da la misma respuesta con respecto a un número determinado. Luego: Existe algún programa BuL finalizable (es decir, alguna función recursiva general) que proporciona exactamente las mismas respuestas que proporciona el método del ser consciente.

La hipótesis central, para darle mayor claridad a esto, es que todo proceso mental que divida los números en dos categorías puede ser descripto bajo la forma de un programa BuL. La convicción intuitiva es la de que no hay más herramientas que las de BuL y que no hay otro procedimiento para usarlas que el de la repetición ilimitada (cosa permitida por BuL). La Tesis Church-Turing no es un hecho demostrable en el sentido en que lo es un teorema matemático: es una hipótesis acerca de los procesos que utiliza el cerebro humano.

La versión procesos públicos

Hay quienes pueden pensar que esta versión se extralimita; sus objeciones rezarían así: “Alguien como el Cangrejo puede existir —alguien con una penetración matemática casi mística, pero que es tan ignorante de sus aptitudes personales como cualquier otro que no las tenga— y quizá los mecanismos mentales de esa persona realizan operaciones que no tienen equivalente en BuL”. La idea, aquí, es que tal vez tenemos un potencial subconsciente para hacer cosas que trascienden los procesos conscientes: cosas inexpresables, en alguna medida, en los términos de las operaciones elementales de BuL. Para estos impugnadores, daremos una versión más débil de la Tesis, la cual distingue entre procesos mentales públicos y privados:

TESIS CHURCH-TURING, VERSIÓN PROCESOS PÚBLICOS: Supongamos que existe un método seguido por un ser consciente para distribuir los números en dos clases. Supongamos, asimismo, que este método produce siempre una respuesta dentro de un lapso finito, y que siempre da la misma respuesta con respecto a un número determinado. Requisito: Supongamos también que este método puede ser comunicado fidedignamente por un ser consciente a otro, por medio del lenguaje. Luego: Existe algún programa BuL finalizable (es decir, alguna función recursiva general) que proporciona exactamente las mismas respuestas que proporciona el método del ser consciente.

Esto nos dice que los métodos públicos están sujetos a “BuLificación”, pero no alude para nada a los métodos privados. No dice que éstos sean inBuLables, pero cuando menos deja la puerta abierta.

Srinivasa Ramanuyan

Como una evidencia contra cualquier versión más exigente de la Tesis Church-Turing, consideremos el caso del famoso matemático indio del primer cuarto de siglo, Srinivasa Ramanuyan (1887-1920). Ramanuyan (figura 105) fue originario de Tamilnadur, en el extremo sur de la India, y estudió algo de matemática en la escuela media. Un día, alguien que había advertido el talento matemático de Ramanuyan le obsequió un manual de análisis, un tanto pasado de moda, que Ramanuyan devoró (figuradamente hablando). Comenzó entonces a hacer sus propias incursiones en el mundo del análisis y, cuando llegó a la edad de veintitrés años, ya había obtenido una cantidad de descubrimientos que él consideraba valiosos. No conoció a nadie con quien compartir sus intereses, pero de alguna manera supo de la existencia de un profesor de matemática, en la remota Inglaterra, llamado G. H. Hardy. Ramanuyan reunió sus mejores exposiciones en un paquete y se las remitió al desprevenido Hardy, junto con una carta que sus amigos le ayudaron a redactar en inglés. Siguen algunos fragmentos de la descripción que hizo Hardy de su reacción ante el hato de papeles recibidos:

… Pronto se hace obvio que Ramanuyan tiene que poseer teoremas mucho más generalizadores y que los ha estado elaborando sin anunciarlo… [Algunas fórmulas] me dejaron completamente anonadado; jamás había visto antes, en absoluto, nada así. Una simple mirada es suficiente para mostrar que únicamente pueden haber sido enunciadas por un matemático del más alto nivel. Por fuerza han de ser verdaderas porque, de no ser así, es imposible que nadie haya tenido la imaginación necesaria para inventarlas. Por último… sin duda el autor es totalmente honesto, porque es más frecuente la aparición de grandes matemáticos que la de plagiarios o embaucadores de habilidad tan pasmosa.^[2]

Como resultado de esto, Ramanuyan se trasladó a Inglaterra, en 1913, con el patrocinio de Hardy, a lo cual siguió un período de intensa colaboración, que terminó con el fallecimiento prematuro de Ramanuyan, a los treinta y tres años, a causa de la tuberculosis.

Ramanuyan tuvo varias características extraordinarias, que lo destacaron de la mayoría de los matemáticos. Una fue su falta de rigor. Muy a menudo afirmaba una conclusión que, según insistía, había llegado a él desde una vaga fuente intuitiva, alejada del dominio de la indagación consciente. Por cierto, muchas veces dijo que la diosa Namagiri lo inspiraba en sueños. Esto ocurrió reiteradamente y, lo que creó los principales equívocos —quizá rodeados por cierta cualidad mística—, fue que muchos de estos “teoremas-intuiciones” eran erróneos. Ahora bien, a veces un hecho del que se podría pensar que, aun cuando no sea provechoso, hace que la gente crédula se tome algo más escéptica, tiene en realidad un efecto inverso: produce un impacto en algún punto vulnerable de aquélla, presionándola con la insinuación de que hay una faceta irracional en la naturaleza humana. Tal fue el caso con los desvaríos de Ramanuyan: muchas personas educadas, ansiosas por depositar su confianza en algo así, consideraron que las facultades intuitivas de Ramanuyan eran evidencia de una penetración mística en la Verdad, y que su falibilidad contribuía, si contribuía a alguna cosa, a fortalecer esa fe, antes que a debilitarla.

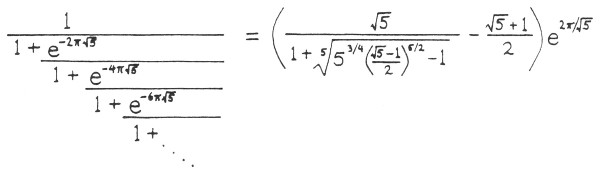
Naturalmente, no fue en detrimento de ello el hecho de que Ramanuyan procediera de una de las regiones más atrasadas de la India, donde se venía practicando el faquirismo y otros ritos misteriosos desde milenios atrás, prácticas cuya extensión, probablemente, siempre fue mayor que la de la enseñanza de matemática superior. Y sus esporádicos relámpagos erróneos de iluminación, en lugar de mostrar a la gente que él no era sino un ser humano, inspiraron la idea de que las equivocaciones de Ramanuyan, paradójicamente, estaban dotadas de cierto género de “veracidad más profunda”; una veracidad “oriental”, capaz, tal vez, de alcanzar verdades inaccesibles a la mente occidental. ¡Qué posibilidad tan deliciosa, casi irresistible! El propio Hardy —quien fuera el primero en negar que Ramanuyan tuviese ninguna clase de poderes místicos— escribió en una oportunidad, acerca de uno de los fracasos de este último: “Y sin embargo no estoy seguro de que, de alguna manera, su fracaso no es más asombroso que ninguno de sus éxitos”.

El otro rasgo sobresaliente de la personalidad matemática de Ramanuyan fue su “amistad con los enteros”, como lo expresó su colega Littlewood. Ésta es una característica compartida, en diversos grados, por un número apreciable de matemáticos, pero que en Ramanuyan se presentaba en medida extrema. Hay un par de anécdotas que ilustran esta especial inclinación. La primera de ellas es relatada por Hardy:

Recuerdo una visita que le hice, cuando se atendía de su enfermedad en Putney. Yo había tomado un taxi cuyo número era el 1729, y le comenté que esa cifra me parecía bastante insulsa, y que esperaba que no implicase un augurio desfavorable. “No”, replicó, “es un número muy interesante; es el menor número expresable como suma de dos cubos, de dos maneras diferentes”. Le pregunté, naturalmente, si conocía la solución del problema correspondiente, relativo a las cuartas potencias; luego de pensar un momento, me respondió que no podía ver ningún ejemplo palpable y que pensaba que el primero de esos números debía ser muy grande.^[3]

Resulta que la respuesta relativa a las cuartas potencias es:

635318657 = 134⁴ + 133⁴ = 158⁴ + 59⁴

El lector puede encontrar atractivo plantearse el problema análogo con respecto a los cuadrados, el cual es mucho más sencillo.

Realmente, es interesante considerar por qué razón Hardy brincó de inmediato a las cuartas potencias; al fin y al cabo, hay varias otras generalizaciones razonablemente naturales de la ecuación

u³ + v³ = x³ + y³

a lo largo de diferentes dimensiones. Por ejemplo, existe la cuestión referida a la representación de un número en tres formas diferentes como la suma de dos cubos:

r³ + s³ = u³ + v³ = x³ + y³.

O bien, se pueden emplear tres cubos diferentes:

u³ + v³ + w³ = x³ + y³ + z³.

O, inclusive, se puede hacer una Gran Generalización en todas las dimensiones a la vez:

r⁴ + s⁴ + t⁴ = u⁴ + v⁴ + w⁴ = x⁴ + y⁴ + z⁴

Hay un sentido, no obstante, en el cual la generalización de Hardy es “la de aspecto más matemático”. ¿Podrá ser programado alguna vez este sentido estético de la matemática?

La otra anécdota aparece en una biografía de Ramanuyan, obra de su compatriota S. R. Ranganathan, bajo el título “La iluminación de Ramanuyan”. Es relatada por el Dr. P. C. Mahalanobis, quien fuera compañero de Ramanuyan en Cambridge, y también de procedencia india.

En su calidad de colaborador más próximo de Ramanuyan, Hardy fue interrogado a menudo, después de la muerte de aquél, sobre si en el estilo de pensamiento del matemático indio hubo elementos de ocultismo o de alguna otra variante esotérica. He aquí uno de sus comentarios al respecto:

Muchas veces se me ha preguntado si Ramanuyan tenía algún secreto especial, si sus métodos eran de un género distinto al de otros matemáticos, si había algo realmente anormal en la modalidad de su pensamiento. No puedo responder con total certidumbre a estas preguntas, pero yo no creo nada de eso. Lo que yo creo es que todos los matemáticos, en el fondo, piensan mediante las mismas modalidades, y que Ramanuyan no fue una excepción al respecto.^[5]

En esencia, aquí Hardy enunció su propia versión de la Tesis Church-Turing. Parafraseo:

TESIS CHURCH-TURING, VERSIÓN DE HARDY: En el fondo, todos los matemáticos son isomórficos.

Esto no hace equivalentes el potencial matemático de los matemáticos y el de las funciones recursivas generales; para eso, todo lo que se necesita es mostrar que la capacidad mental de algún matemático no es más general que las funciones recursivas. Luego, si se da crédito a la Versión de Hardy, ya se sabe eso con respecto a todos los matemáticos.

Después, Hardy compara a Ramanuyan con la prodigiosidad de las calculadoras:

Su memoria y sus aptitudes para el cálculo eran muy inusuales, pero no podrían ser consideradas “fuera de lo normar. Si tenía que multiplicar dos números extensos, lo hacía en la forma ordinaria; podía multiplicar con una rapidez y una exactitud desacostumbrada, pero no con mayor rapidez y exactitud que cualquier matemático dotado de rapidez natural y habituado a hacer cómputos.^[6]

Hardy señala los atributos intelectuales salientes que él percibía en Ramanuyan:

A su memoria, su paciencia y sus facultades de cálculo, sumaba una capacidad de generalización, un sentimiento de la forma y una aptitud para la rápida modificación de sus hipótesis, que provocaban muchas veces asombro, e hicieron de él, en su campo, alguien inigualable en su época.^[7]

Las partes del pasaje precedente que he subrayado, según mi opinión, constituyen una caracterización excelente de algunos de los rasgos más sutiles de la inteligencia en general. Finalmente, Hardy concluye un tanto nostálgicamente:

[Su obra] no tiene la simplicidad y la inevitabilidad de las obras verdaderamente mayores; hubiera sido más grande de haber sido menos extraña. Tiene una virtud que nadie puede negarle: una profunda e invicta originalidad. Probablemente hubiera sido más importante como matemático si, en su juventud, hubiese recibido un poco más de comprensión y de orientación: hubiera hecho más aportes originales y, sin duda, de mayor significación. Por otro lado, así hubiera sido menos un Ramanuyan, y más un profesor europeo, y en tal caso quizá la pérdida hubiera sido superior a la ganancia.^[8]

La manera romántica en que Hardy se expresa acerca de Ramanuyan revela la gran estima que sentía por él.

“Idiots savants”

Hay otra clase de gente cuyas habilidades matemáticas parecen desafiar las explicaciones racionales: los llamados así “idiots savants”, quienes pueden efectuar, mentalmente (o como sea que lo hacen), complejos cálculos a la velocidad del rayo. Johann Martin Zacharias Dase, quien vivió entre 1824 y 1861, y fue contratado por varios gobiernos europeos para realizar cómputos, es un ejemplo destacado. No sólo podía multiplicar dos números de 100 dígitos cada uno en su cabeza, sino que también tenía un misterioso sentido de la cantidad; es decir, él podía “saber”, sin contar, cuántas ovejas había en un campo, o palabras en una oración, etc., hasta el límite de, aproximadamente, 30, en tanto que la mayoría de nosotros posee ese sentido pero sólo hasta el límite de, aproximadamente, 6. Al margen, Dase no era un idiota.

No detallaré la gran cantidad de fascinantes casos documentados de “calculistas relámpago”, pues ello se aparta de mis propósitos. Pero creo que es importante disipar la idea de que aquéllos emplean algún método misterioso e inanalizable. Aunque es frecuente el caso de que sus aptitudes brujeriles para el cálculo superen con mucho la aptitud de sus sujetos para explicar sus resultados, alguna vez aparece una persona poseedora de otros dones intelectuales, a los que suma el tipo de habilidad espectacular con los números de que estamos hablando. La introspección practicada por estas personas, junto con una amplia investigación psicológica, han permitido establecer que no tiene lugar ninguna cosa de tipo esotérico durante los procesos propios de los calculistas relámpago, sino que, simplemente, sus mentes vuelan a través de los pasos intermedios con la misma autoconfianza de un atleta que ejecuta un movimiento complicado en forma veloz y graciosa. No obtienen sus respuestas gracias a alguna suerte de resplandor de iluminación (pese a que, subjetivamente, algunas de ellas puedan sentirlo así) sino —lo mismo que el resto de los mortales— gracias al cálculo secuencia), lo cual equivale a decir, gracias a un proceso de BuLeamiento (o de BuDeamiento).

Cabe decir que una de las pruebas más obvias de que no hay allí ninguna “línea directa con Dios” la brinda el hecho de que, cuando los números abarcados se hacen mayores, las respuestas se producen con mayor lentitud. Es de presumir que, si Dios o un “oráculo” estuviesen proporcionando las soluciones, no tendría por qué haber ninguna demora frente a números más extensos. Probablemente se pueda elaborar un prolijo diseño que muestre cómo varían los lapsos de respuesta de un calculista relámpago según las dimensiones de los números comprendidos, y de las operaciones involucradas, y a partir de allí deducir algunos rasgos de los algoritmos empleados.

La versión isomorfismo de la Tesis Church-Turing

Esto, finalmente, nos suministra una versión habitual, fortalecida, de la Tesis Church-Turing:

TESIS CHURCH-TURING, VERSIÓN ISOMORFISMO: Supongamos que existe un método seguido por un ser consciente para distribuir los números en dos clases. Supongamos, asimismo, que este método produce siempre una respuesta dentro de un lapso finito, y que siempre da la misma respuesta con respecto a un número determinado. Luego: Existe algún programa BuL Analizable (es decir, alguna función recursiva general) que proporciona exactamente las mismas respuestas que proporciona el método del ser consciente. Además: El proceso mental y el programa BuL son isomórficos, en el sentido de que, en algún nivel, hay una correspondencia entre los pasos que son cumplidos en la computadora y en el cerebro.

Adviértase que no sólo ha sido reforzada la conclusión sino que, asimismo, ha sido eliminado el requisito de comunicabilidad de la pusilánime Versión Procesos Públicos. Solamente hablaremos de esta audaz versión, en adelante.

En resumen, esta versión afirma que, cuando hacemos cualquier cómputo, nuestra actividad mental puede ser reflejada isomórficamente por algún programa BuL. Aclaremos muy bien que esto no significa que el cerebro esté procesando un programa BuL, formulado en el lenguaje BuL completo con sus COMIENZO, FIN, INTERRUMPIR, y todo lo demás: en absoluto. Sólo se trata de que los pasos son seguidos en el mismo orden que podrían haber seguido en un programa BuL, y que la estructura lógica del cálculo puede ser reflejada en un programa BuL.

Ahora bien, para que esta idea adquiera sentido, tendremos que hacer algunas distinciones de niveles tanto en la computadora como en el cerebro, pues de otro modo podría ser interpretada como un cabal sinsentido. Presumiblemente, los pasos mediante los cuales avanza el cálculo dentro de la cabeza de una persona están ubicados en el nivel más alto, y se apoyan en niveles más bajos, y en último término en el hardware. Entonces, si hablamos de isomorfismo, ello quiere decir que, tácitamente, hemos supuesto que el nivel más alto puede ser aislado, permitiéndonos así analizar qué sucede allí, independientemente de los restantes niveles, y luego hacer corresponder ese nivel superior con BuL. Más exactamente, la suposición consiste en que hay entidades software que cumplen las funciones de diversas construcciones matemáticas, y que son activadas en formas que pueden ser reflejadas con exactitud dentro de BuL (véase la figura 106). Lo que hace posible la existencia de estas entidades software es toda la infraestructura detallada en los Capítulos XI y XII, como también en el Preludio y Furmiga. No se sugiere ninguna actividad isomórfica en los niveles inferiores del cerebro y de la computadora (esto es, neuronas y bits).

El espíritu de la Versión Isomorfismo, si no su letra, se hace comprensible si decimos que, lo que hace un idiot savant cuando calcula, pongamos por caso el logaritmo de π, es isomórfico de lo que hace una minicalculadora cuando calcula la misma cosa, con la aclaración de que el isomorfismo se circunscribe al nivel de los pasos aritméticos, y no se proyecta a los niveles más bajos de, para la primera situación, las neuronas y, en la segunda, de los circuitos integrados. (Por supuesto, se pueden seguir diferentes rutas en cualquier clase de cálculo, pero ha de presumirse que el calculista mecánico, si no el humano, puede ser instruido para que calcule la respuesta con arreglo a una modalidad determinada).

La representación del conocimiento relativo al mundo real

Ahora bien, esto parece muy aceptable cuando el dominio al que se refiere es el de la teoría de los números, pues allí el universo entero donde suceden las cosas es muy reducido y claro. Sus fronteras, sus moradores y sus reglas están bien definidos, como en un laberinto rigurosamente diseñado. Un mundo así es sumamente menos complicado que el ilimitado y mal definido mundo que habitamos. Un problema de teoría de los números, luego de enunciado, está completo en y por sí; un problema del mundo real, en cambio, nunca queda confiablemente tabicado con respecto a ninguna región del mundo. Por ejemplo, la tarea de cambiar una bombilla de luz quemada puede hacer necesario el desplazamiento de un saco de desperdicios; esto, a su vez, puede causar el derramamiento inesperado de una caja de grageas, lo cual entonces obligará a barrer el piso para que el bebé no recoja y se coma alguna de las grageas diseminadas, etc., etc. Las grageas y los desperdicios y el bebé y la bombilla quemada son todos elementos con una relación muy distante entre sí, dentro del mundo; sin embargo, un hecho cotidiano los reúne estrechamente. Ni qué decir acerca de cuántas cosas más podrían incorporarse a esta conexión, con la sola ocurrencia de otras leves variantes con respecto a lo esperado. Por el contrarío, frente a un problema de teoría de los números, jamás hará falta terminar analizando cosas tan heterogéneas como grageas o bebés o sacos de basura o escobillones con la finalidad de resolver el problema planteado. (Por supuesto, el conocimiento intuitivo de estos objetos puede ser una ayuda eficaz cuando se trata, inconscientemente, de elaborar imágenes mentales que contribuyan a visualizar el problema en términos geométricos: pero éste es otro problema).

A causa de la complejidad del mundo, es difícil imaginar una minicalculadora que responda a preguntas que se le planteen mediante la presión de botones rotulados “bebé”, “desperdicios”, “bombilla”, etc. En realidad, es un extremo complicado de conseguir, hasta la fecha, que una computadora de tamaño normal y alta velocidad responda a preguntas que, para nosotros, caben en subdominios muy simples del mundo real. Podemos comparar los procesos mentales vinculados al mundo real con un árbol cuya parte visible se levanta vigorosamente desde el suelo, pero que depende vitalmente de sus raíces invisibles, extendidas subterráneamente, las cuales le brindan estabilidad y nutrición. Las raíces simbolizan los complejos procesos que tienen lugar por debajo del nivel consciente de la mente, procesos cuyos efectos inciden sobre el modo en que pensamos, pero de los cuales no nos apercibimos. Se trata de los “patrones desencadenantes de símbolos”, aludidos en los Capítulos XI y XII.

Pensar en el mundo real es algo absolutamente distinto de lo que ocurre cuando multiplicamos dos números; en este caso, todo está abierto al examen, “por sobre el suelo”, por decir así. En aritmética, el nivel superior puede ser separado limpiamente e instrumentado con la misma eficacia en muy diferentes clases de hardware: máquinas sumadoras, minicalculadoras, grandes computadoras, cerebros humanos, etc. A esto se refiere la Tesis Church-Turing. Pero cuando arribamos a la comprensión del mundo real, pareciera no haber forma de separar el nivel superior y programarlo independientemente. Los patrones desencadenantes de símbolos son extraordinariamente complejos. Sin duda, hay diversos niveles a través de los cuales “se infiltran” y “brotan” los pensamientos.

Ocurre que —y esto nos permite al tema principal de los Capítulos XI y XII— la representación del mundo real en el cerebro, pese a estar enraizada, en determinado grado, en el isomorfismo, abarca ciertos elementos que no tienen equivalentes en el mundo exterior. Esto es, allí hay algo más simples estructuras mentales representativas de “bebé”, “escoba”, etc. Por cierto que todos estos símbolos existen: pero sus estructuras internas son extremadamente complejas y están cerradas, en una medida considerable, a la inspección consciente. Además, sería en vano esforzarse por tender una correspondencia entre la estructura interna de un símbolo, y un rasgo específico dado del mundo real.

Procesos no separables

Por todo ello, el cerebro comienza a impresionar como un sistema formal muy singular, pues en el nivel de base —el nivel neural, allí donde operan las “reglas” y cambian los estados— no puede haber interpretación de los elementos primordiales (la excitación de las neuronas o, inclusive, acontecimientos de nivel aún inferior). Sin embargo, en el nivel superior emerge una interpretación significativa: una correspondencia entre las grandes “nubes” de actividad neural, a las cuales hemos estado llamando “símbolos”, y el mundo real. Hay alguna semejanza con la construcción Gödel en el sentido de que un isomorfismo de alto nivel permite que un alto nivel de significación pueda ser articulado en cadenas; sin embargo, en la construcción Gödel, los significados de alto nivel “corren” sobre los niveles más bajos; es decir, son derivados del nivel más bajo luego de introducida la noción de numeración Gödel. No así en el cerebro, donde los hechos de nivel neural no están sujetos a una interpretación del tipo mundo real; sencillamente, esos hechos no son imitadores de ninguna cosa, son el puro sustrato que da apoyo al nivel más alto, así como los transistores de una minicalculadora son el puro soporte de su actividad de representación numérica. Y lo que se deduce es que no hay forma de separar con limpieza el nivel más alto y elaborar una copia isomórfica del mismo, con destino a un programa; si tenemos que reflejar los procesos cerebrales que permite la comprensión del mundo real, debemos reflejar determinadas cosas que tienen lugar en el nivel más bajo: los “lenguajes del cerebro”. Esto no significa, necesariamente, que se deba recorrer íntegro el camino que lleva hasta el nivel del hardware, pese a que, eventualmente, ese pueda ser el caso.

Si se desarrolla un programa cuyo objetivo sea obtener una “inteligente” (a saber, al modo humano) representación interna de lo que hay “allí”, en algún punto, probablemente se presente la obligación de utilizar estructuras y procesos que escapan a cualquier interpretación directa, es decir, que no admiten una correspondencia transparente con elementos de la realidad. Estos estratos inferiores del programa podrán ser entendidos solamente en virtud de su relación catalítica con los estratos situados encima suyo, y no en función de alguna vinculación directa con el mundo exterior. (Una imagen concreta de esta situación fue propuesta por el Oso Hormiguero en la Furmiga: la “pesadilla indescriptiblemente aburrida” de ensayar la comprensión de un libro limitándose al nivel de las letras).

Personalmente, me inclinaría por conjeturar que tal arquitectura multinivel de los sistemas que manejan conceptos se hace necesaria en el momento preciso en que los procesos que involucran imágenes y analogías pasan a ser elementos significativos del programa, en oposición a los procesos de los cuales se da por supuesto que realizan razonamientos estrictamente deductivos. Los procesos que desarrollan razonamientos deductivos pueden ser programados en, esencialmente, un solo nivel; por definición, en consecuencia, son separables. De acuerdo a mi hipótesis, entonces, los procesos de la imaginación y del pensamiento analógico requieren diversas capas de sustratos y, en consecuencia, son intrínsecamente no separables. Creo, además, que es precisamente en ese mismo punto donde la creatividad comienza a surgir, lo cual implicaría que ésta reposa, intrínsecamente, en ciertos acontecimientos “ininterpretables” de menor nivel. Las capas de sustentamiento del pensamiento analógico son, por supuesto, del máximo interés: ofreceremos algunas especulaciones sobre su naturaleza en los dos capítulos siguientes.

Artículos de fe reduccionista

Una forma de analizar la relación existente entre los niveles superiores e inferiores del cerebro es la que sigue: sería posible armar una red neural que, en un nivel local (neurona a neurona), actúe de manera indiferenciable con respecto a una red neural del cerebro, pero que carecería por completo de significación de nivel más alto. El hecho de que el nivel más bajo esté compuesto por neuronas en interacción no fuerza de ninguna manera la aparición de un nivel significativo más alto: del mismo modo que, en una sopa de letras, la presencia de éstas fuerza, cuando mucho, a encontrar enunciaciones significativas nadando en el plato. La significación de alto nivel es un accesorio opcional de una red neural, un accesorio que es generado como consecuencia de las presiones ambientales de la evolución.

La figura 107 es un diagrama que ilustra el hecho de que esa emergencia de un nivel de significación más alto es optativa. La flecha dirigida hacia arriba indica que puede aparecer un sustrato que carezca de un nivel mayor de significación, pero no a la recíproca: el nivel más alto debe derivarse de las propiedades de un nivel más bajo.

El diagrama incluye una indicación sobre la simulación, por una computadora, de una red neural. Esto es, en principio, practicable, por muy complicada que sea la red, a condición de que el comportamiento individual de las neuronas pueda ser descripto en términos de computación que una computadora pueda procesar; se trata de un postulado sutil que poca gente, además, cree cuestionable. Sin embargo, es una muestra de “fe reduccionista”, que podría ser considerada una “versión microscópica” de la Tesis Church-Turing. La enunciamos explícitamente a continuación:

TESIS CHURCH-TURING, VERSIÓN MICROSCÓPICA: El comportamiento de los componentes de un ser vivo puede ser simulado en una computadora. Esto es, el comportamiento de cualquier componente (del cual se supone, habitualmente, que es la célula) puede ser calculado por un programa BuL (es decir, una función recursiva general) con el grado de exactitud que se requiera, dada una descripción lo suficientemente precisa del estado interno de los componentes y de su ámbito inmediato.

Esta versión de la Tesis Church-Turing dice que los procesos cerebrales no poseen más ingredientes místicos —aun cuando sí posean más niveles de organización— que, pongamos por caso, los procesos estomacales. Es impensable, en este momento y en esta época, la sugerencia de que dirigimos nuestro alimento, no mediante procesos químicos ordinarios, sino por la intervención de una suerte de misteriosa y mágica “asimilación”. Esta versión se limita a extender ese razonamiento de sentido común a los procesos cerebrales; en resumen, expresa la fe de que el cerebro opera en una forma que es, en principio, comprensible. Es una muestra de fe reduccionista.

Lo que sigue es un corolario a la Tesis CT Microscópica, consistente en esta, bastante breve, versión macroscópica:

TESIS CHURCH-TURING, VERSIÓN REDUCCIONISTA: Todos los procesos cerebrales se derivan de un sustrato computable.

La afirmación anterior se refiere al sustento teórico más sólido que sea posible aportar en apoyo de la posibilidad eventual de dar vida a la Inteligencia Artificial.

Por supuesto, las investigaciones en Inteligencia Artificial no están dirigidas a simular redes neurales, porque se basan en otra clase de fe: la de que, probablemente, existen rasgos significativos de inteligencia que pueden ser ubicados al tope de sustratos totalmente diferentes a los propios de los cerebros orgánicos. La figura 108 muestra una suposición de relaciones entre Inteligencia Artificial, inteligencia natural y mundo real.

¿Progresos paralelos en IA y en simulación cerebral?

La idea de que, para culminar con éxito los trabajos en IA, tenga que ser simulado alguna vez el hardware propiamente dicho del cerebro es, hasta hoy al menos, digna de total rechazo por parte de los investigadores de IA. Sin embargo, uno podría preguntarse: “¿Cómo, exactamente, nos será necesario copiar el cerebro para obtener IA?”. La respuesta real es que ello depende, quizá, de cuántos rasgos de la conciencia humana son los que queremos simular.

¿La capacidad de jugar bien a las damas es un indicador suficiente de inteligencia? Si es así, IA entonces ya existe, puesto que los programas para jugar a las damas corresponden a la clase mundo real. ¿O bien la inteligencia es la aptitud para integrar funciones simbólicamente, como en la clase estudiante de cálculo de primer año? Si es así, IA entonces ya existe, puesto que las rutinas de integración simbólica superan, en muchos casos, a la gente más capacitada. ¿O la inteligencia será el don de jugar bien al ajedrez? Si es así, IA entonces está perfectamente orientada, puesto que los programas para jugar al ajedrez pueden derrotar a la mayoría de los aficionados más hábiles, y es probable que el nivel del ajedrez artificial continúe, poco a poco, mejorando.

Históricamente, se ha dado una actitud particular acerca de las cualidades que, si son mecanizadas, constituirían fuera de duda la inteligencia. Pareciera a veces como si cada paso hacia IA, en lugar de producir algo que cualquiera aceptaría como inteligencia real, simplemente revelara qué cosa no es la inteligencia real. Si la inteligencia implica aprendizaje, creatividad, respuestas emocionales, sentido de la belleza, sentido de sí mismo, queda por delante un largo camino que debe ser recorrido, y es posible que ello se logre únicamente cuando hayamos duplicado totalmente un cerebro vivo.

La belleza, el Cangrejo y el espíritu

Ahora bien, ¿qué nos dice todo esto —si es que dice algo— a propósito de la actuación del Cangrejo como virtuoso, ante Aquiles? Aquí hay dos temas entremezclados, los siguientes:

1. Cualquier proceso cerebral, bajo cualesquiera circunstancias, ¿podría distinguir en forma totalmente segura entre enunciados verdaderos y falsos de TNT, sin caer en violaciones de la Tesis Church-Turing? ¿O se trata de un acto, en principio, imposible?
2. La percepción de la belleza, ¿es un proceso cerebral?

Primero de todo, en respuesta a (1): si se permiten violaciones a la Tesis Church-Turing, no parece haber ninguna objeción fundamental que presentar a los extraños sucesos acaecidos en el Diálogo. De manera que estamos interesados en saber si un creyente en la Tesis Church-Turing descreería de los talentos del Cangrejo. Bueno, todo depende de cuál sea la versión de la Tesis CT en la que se crea. Por ejemplo, si uno se adhiere exclusivamente a la Versión Procesos Públicos, puede fácilmente compatibilizar con ella el comportamiento del Cangrejo, mediante la afirmación de que las aptitudes del Cangrejo no son comunicables. Contrariamente, si uno adopta la Versión Reduccionista, le costará mucho creer en las supuestas virtudes del Cangrejo (a causa del Teorema de Church, próximo a ser demostrado). Creer en las versiones intermedias permite cierto grado de dilución del tema. Por supuesto, modificar la posición de acuerdo a las conveniencias lo hace todo más cómodo.

En este momento, parece adecuado presentar una nueva versión de la Tesis CT, la cual es sostenida implícitamente por una vasta cantidad de personas, y que ha sido públicamente expuesta por diversos autores, de varias maneras distintas. Algunos de los más famosos, entre estos últimos, son los siguientes: los filósofos Hubert Dreyfus, S. Jaki, Mortimer Taube y J. R. Lucas; el biólogo y filósofo Michael Polanyi (un holista por excelencia); el destacado neurofisiólogo australiano John Eccles. Estoy seguro de que muchos otros autores han formulado reflexiones similares, y de que son incontables los lectores que las han acogido favorablemente. Lo que intento un poco más abajo es presentar una síntesis de sus posiciones; es muy posible que incurra en alguna dosis de injusticia, pero he tratado de transmitir el espíritu de la cosa con el mayor rigor de que soy capaz:

TESIS CHURCH-TURING, VERSIÓN ESPIRITUALISTA: Algunas de las tareas que cumple el cerebro pueden ser objeto de vagas aproximaciones por parte de una computadora, pero no ocurrirá así con las principales, y tampoco, ciertamente, con las interesantes. De todas maneras, aun cuando lo consiguieran, dejarían sin explicar el espíritu, y no hay forma de que las computadoras obtengan un sustento que las habilite para ello.

Esta versión se relaciona con la anécdota del Magnificangrejo de dos maneras. En primer lugar, los adherentes de aquélla consideran, tal vez, que el relato es disparatado e inverosímil, aunque, en principio, no ilegítimo. En segundo lugar, dichos adherentes sostendrán, es posible, que la apreciación de cualidades tales como la belleza es una de las propiedades vinculadas a la elusividad del espíritu y, por consiguiente, inherentemente asequible sólo a los seres humanos, no a las simples máquinas.

Volveremos enseguida a este segundo punto, pero antes, puesto que estamos en el tópico del espiritualismo, debemos exponer una última versión, en una forma aún más extrema, debido a que es la forma postulada por incontables personas cultas en nuestros días:

TESIS CHURCH-TURING, VERSIÓN THEODORE ROSZAK: Las computadoras son ridículas. Lo mismo que la ciencia en general.

Este punto de vista tiende a prevalecer entre determinada gente dispuesta a ver una amenaza a los valores humanos en cualquier cosa que se asocie remotamente con los números o con la exactitud. Es muy lamentable que esta gente no estime la profundidad, la complejidad y la belleza envueltas en la exploración de estructuras abstractas tales como la mente humana, donde, por cierto, se llega a un contacto íntimo con las interrogaciones últimas acerca de qué es el ser humano.

Retornando a la belleza, poco atrás planteamos si la apreciación de la misma es un proceso cerebral y, de ser así, si es imitable por una computadora. Quienes creen que esto no es explicado por el cerebro es muy difícil que acepten que una computadora pueda poseer tal apreciación. Quienes creen que se trata de un proceso cerebral vuelven a dividirse, con arreglo a la versión de la Tesis CT por la cual opten. Un reduccionista absoluto creerá que, en principio, cualquier proceso cerebral puede ser convertido en un programa de computadora; otros, sin embargo, pueden entender que la de belleza es una noción demasiado mal definida como para que un programa de computadora pueda asimilarla. Quizá sienten que la apreciación de la belleza requiere un elemento de irracionalidad, por lo tanto incompatible con la sustancia misma de las computadoras.

Lo irracional y lo racional pueden coexistir en diferentes niveles

Empero, este criterio de que “la irracionalidad es incompatible con las computadoras” reposa sobre una grave confusión de niveles. El error se origina en la idea de que, como las computadoras son máquinas que funcionan sin equivocarse, están confinadas a ser “lógicas” en todos los niveles. Sin embargo, es enteramente obvio que una computadora puede ser instruida para que dé salida impresa a una secuencia de enunciados ilógicos o, para variar, una tanda de enunciados que tengan valores arbitrarios de verdad. Claro que, siguiendo tales instrucciones, ¡una computadora no estaría cometiendo errores! Por el contrario, únicamente habría error si la máquina diese salida a algo que no fuese el tipo de enunciado que, según las instrucciones recibidas, debe imprimir. Esto ilustra el modo en que el funcionamiento sin equivocaciones en un nivel puede estar dando fundamento a la manipulación simbólica operada en un nivel más alto… y los objetivos de este nivel superior puede que no tengan nada que ver con la difusión de la Verdad.

Otro medio para ampliar el panorama a propósito de esto es recordar que un cerebro, también, es una colección de elementos que funcionan sin equivocarse: las neuronas. Toda vez que el umbral de una neurona es sobrepasado por la suma de las señales que ingresan, ¡PUM!: se excita. Nunca sucede que una neurona olvide sus conocimientos aritméticos, es decir, que sume negligentemente sus entradas y extraiga un resultado equivocado. Inclusive cuando muere, una neurona continúa funcionando correctamente, en el sentido de que sus componentes siguen obedeciendo las leyes de la matemática y de la física. No obstante, como bien sabemos, las neuronas son perfectamente capaces de sustentar comportamientos de alto nivel que son erróneos, en su nivel propio, e inclusive en una medida sorprendente. La figura 109 pretende ilustrar esta colisión entre niveles: una creencia incorrecta, afirmada en el ámbito del software de una mente, sustentada en el hardware de un cerebro que funciona sin equivocarse.

Esta cuestión —ya varias veces tocada en diversos contextos— radica simplemente en que la significación puede tener existencia en dos o más niveles diferentes de un sistema que opere símbolos; junto con la significación, ocurre lo mismo en el caso del acierto y del desacierto. La presencia de la significación en un nivel dado está determinada por la circunstancia de si la realidad es reflejada o no, de una manera isomórfica (o aún menos definida), en ese nivel. Luego, el hecho de que las neuronas siempre efectúen sumas correctas (en realidad, son cálculos mucho más complejos) no asegura en absoluto la corrección de las conclusiones que tienen lugar en el nivel superior, nivel sustentado en la maquinaria neuronal. Si el nivel máximo de alguien está ocupado en demostrar kōans de budismo booleano o en meditar sobre los teoremas del álgebra zen, sus neuronas están funcionando racionalmente. Por lo mismo, los procesos simbólicos de alto nivel que crean, en el cerebro, la experiencia de apreciación de la belleza, son perfectamente racionales en el nivel básico, donde tiene lugar el funcionamiento sin equivocaciones; cualquier irracionalidad, en caso de que la haya, se produce en el nivel más alto, y es un epifenómeno —una consecuencia— de los acontecimientos del nivel más bajo.

Para enfocar el mismo asunto en una forma diferente, supongamos que a nuestra mente le está costando resolver el problema de si ordenar un emparedado de queso o de jamón. ¿Esto implica que también nuestras neuronas están en la incertidumbre, sin determinar si deben excitarse o no? Por supuesto que no: nuestra confusión gastronómica es un estado de alto nivel que descansa por completo en la eficiente excitación de miles de neuronas, a través de maneras sumamente organizadas. Aunque ello sea un tanto paradójico, se hace evidente a poco que se lo piense; sin embargo, quizá sea legítimo decir que casi todas las confusiones en materia de mentes y computadoras tienen su origen en confusiones de niveles tan elementales como la mencionada.

No hay razón para creer que el hardware de funcionamiento infalible de una computadora no pueda ser soporte de un comportamiento simbólico de alto nivel, el cual representaría estados complejos tales como la confusión, los olvidos o la apreciación de la belleza. Ello requerirá la existencia de subsistemas masivos que interactúen entre sí de acuerdo a una “lógica” compleja. La conducta visible puede aparecer como racional o como irracional, pero por debajo suyo y dándole concreción habrá un hardware confiable y lógico.

Más argumentos en contra de Lucas

Al mismo tiempo, esta distinción de niveles nos suministra una nueva provisión de combustible para seguir refutando a Lucas. La argumentación de Lucas está basada en la noción de que el Teorema de Gödel, por definición, es aplicable a las máquinas. De hecho, Lucas ha formulado al respecto un pronunciamiento notablemente enfático:

El Teorema de Gödel debe aplicarse a las máquinas cibernéticas, porque está en la esencia de las máquinas el que sean la instrumentación concreta de un sistema formal.^[9]

Como ya vimos, esto es correcto con respecto al nivel del hardware; no obstante, como consecuencia de que puede haber niveles más altos, no se trata de la última palabra con relación al tema. Pero Lucas da la impresión de que, en las máquinas imitadoras de la mente de las cuales él habla, existe solamente un nivel como escenario de la manipulación simbólica. Por ejemplo, la Regla de Separación (llamada “Modus Ponens” en su artículo) sería instalada en el hardware y pasaría a ser un aspecto inmodificable de dicho tipo de máquinas. Va todavía más allá e insinúa ser un pilar inmutable del sistema mecánico:

El sistema dejaría de ser un sistema lógico formal, y la máquina quedará escasamente capacitada para presentarse como modelo de la mente.^[10]

Ahora bien, muchos de los programas que son desarrollados en IA tienen muy poco en común con los programas que generan verdades de teoría de los números: programas con reglas de inferencia inflexibles y grupos fijos de axiomas. No obstante, se les asigna con certidumbre el carácter de “modelos de la mente”. En su nivel máximo —el nivel “informal”— puede haber manipulación de imágenes, formulación de analogías, olvido de ideas, confusión de conceptos, desdibujamiento de distinciones, etcétera. Pero esto no contradice el hecho de que todos esos fenómenos descansan en el correcto funcionamiento de su hardware subyacente, tal cual como el cerebro descansa en el correcto funcionamiento de sus neuronas. De modo pues que los programas IA son, por cierto, “instrumentaciones concretas de un sistema formal”, pero no son máquinas a las cuales pueda aplicarse la transmutación lucasianas de la prueba de Gödel. La argumentación de Lucas se aplica exclusivamente a su nivel básico, aquel donde su inteligencia —grande o limitada— no reposa.

Hay una circunstancia a través de la cual Lucas traiciona su ultrasimplificada visión relativa al modo en que los procesos mentales estarían representados dentro de los programas de computadora. Hablando del tema de la coherencia, escribe:

Si fuéramos, en realidad, máquinas incoherentes, estaríamos perfectamente satisfechos con nuestra incoherencia, y afirmaríamos con toda soltura los dos términos de una contradicción. Además, estaríamos dispuestos a decir absolutamente cualquier cosa: lo cual no es así. Se ha mostrado con facilidad que en un sistema formal incoherente es demostrable cualquier cosa.^[11]

La última oración revela la suposición de Lucas en el sentido de que, en forma necesaria, todo sistema formal que desarrolle razonamientos debe incluir en su interior el cálculo preposicional. En particular, él está considerando el teorema <<P∧~P>⊃Q> del cálculo preposicional; evidentemente, parte de la errónea creencia de que se trata de un rasgo inevitable del razonamiento mecanizado. Sin embargo, es perfectamente verosímil que los procesos del pensamiento lógico, como puede serlo un razonamiento preposicional, surjan como consecuencia de la inteligencia general de un programa IA, y no por haber sido preprogramados. ¡Esto es lo que sucede en los seres humanos! Y no existe ningún motivo específico conducente a suponer que el cálculo preposicional estricto, con sus rígidas reglas y la muy simple definición de coherencia que éstas transmiten, emergería de dicho programa.

Una columna de apoyo de IA

Podemos sintetizar los resultados de este paseo por el ámbito de la distinción de niveles lanzando una versión final y más enérgica de la Tesis Church-Turing:

TESIS CHURCH-TURING, VERSIÓN IA: Los procesos mentales de toda índole pueden ser simulados por un programa de computadora cuyo lenguaje subyacente tenga un poder igual al de BuL: es decir, donde todas las funciones recursivas parciales puedan ser programadas.

Es necesario señalar que, en la práctica, muchos investigadores de IA se fundan en otro artículo de fe, íntimamente relacionado con el propuesto por la Tesis CT, al cual denomino Tesis IA. Dice más o menos así:

TESIS IA: Cuando la inteligencia de la máquina evoluciona, sus mecanismos subyacentes tienden a asemejarse a los mecanismos que subyacen a la inteligencia humana.

En otras palabras, todas las inteligencias no son sino variaciones de un mismo tema; para crear inteligencia verdadera, la investigación en IA no tiene más que seguir avanzando hacia niveles cada vez más bajos, más y más próximos a los mecanismos cerebrales, si es que su objetivo consiste en dotar a sus máquinas de las aptitudes propias de los seres humanos.

Teorema de Church

Volvamos al Cangrejo y a la pregunta de si su procedimiento de decisión con respecto a la teoremidad (presentado bajo el disfraz de un tamiz para la belleza musical) es compatible con la realidad. En verdad, no hay forma de deducir, a partir de los acontecimientos ocurridos en el Diálogo, si el don del Cangrejo es una capacidad para distinguir entre teoremas y no teoremas o, en forma alternativa, una capacidad para distinguir entre enunciados verdaderos y falsos. Por supuesto, en muchos casos ambas cosas son equivalentes, pero el Teorema de Gödel muestra que no siempre es así. No hay problema sin embargo: las dos alternativas son imposibles, si uno cree en la Versión IA de la Tesis Church-Turing. La proposición según la cual es imposible contar con un procedimiento de decisión para aplicar a la teoremidad en todo sistema formal que tenga el poder de TNT es conocida como Teoremas de Church. La proposición según la cual es imposible contar con un procedimiento de decisión para aplicar a las verdades teórico-numéricas —si es que existen tales verdades, cosa que uno pone en duda luego de recorrer todas las bifurcaciones de TNT— es una consecuencia inmediata del Teorema de Tarski (publicado en 1933, aunque las ideas que contiene fueron manejadas por Tarski mucho antes).

Las demostraciones respectivas de estas dos importantísimas conclusiones metamatemáticas son muy similares; ambas se siguen con rapidez de los desarrollos autorreferenciales.

Consideremos primero la cuestión relativa al procedimiento de decisión para la teoremidad TNT. Si existiera un recurso uniforme que permitiera a las personas hacer recaer cualquier fórmula dada X en la clase “teorema” o en la clase “no teorema”, en virtud de la Tesis CT (Versión Habitual), habría entonces un programa BuL finalizable (una función recursiva general) que podría adoptar la misma decisión, cuando recibe como entrada el número Gödel de la fórmula X. El paso crucial es recordar que toda propiedad que puede ser verificada mediante un programa BuL finalizable está representada en TNT. Esto significa que la propiedad de teoremidad TNT estaría representada (por oposición a estar simplemente expresada) en el interior de TNT. Como veremos dentro de un momento, empero, esto nos metería en una encrucijada, pues si la teoremidad es un atributo representable, la fórmula G de Gödel se convertiría en algo tan tautológico como la paradoja de Epiménides.

Todo gira en tomo a lo que dice G: “G no es un teorema de TNT”. Supongamos que G fuera un teorema; luego, puesto que la teoremidad es supuestamente representable, la fórmula TNT que afirma “G es un teorema” sería un teorema de TNT. Pero esta fórmula es ~G, la negación de G, de manera que TNT es incoherente. Por el otro lado, supongamos que G no fuera un teorema; luego, una vez más gracias a la respuesta representabilidad de la teoremidad, la fórmula que afirma “G no es un teorema” sería un teorema de TNT. Pero esta fórmula es G, e ingresamos de nuevo en la paradoja. A diferencia de la situación anterior, no hay resolución de la paradoja. El problema es creado por la suposición de que la teoremidad es representada por alguna fórmula de TNT; en consecuencia, debemos retroceder sobre nuestros pasos y suprimir dicha suposición. Esto nos obliga a concluir que ningún programa BuL puede discriminar entre números Gödel de teoremas y de no teoremas. Para terminar, si aceptamos la Versión IA de la Tesis CT, debemos retroceder entonces aún más, y concluir que ningún método, sea el que fuere, puede habilitar a los seres humanos a distinguir con seguridad entre teoremas y no teoremas: y esto incluye las determinaciones basadas en la belleza. Quienes se adhieren exclusivamente a la Versión Procesos Públicos pueden seguir pensando que las capacidades del Cangrejo son posibles: de todas las versiones, sin embargo, ésta es quizá la más difícil de fundamentar.

Teorema de Tarski

Pasemos ahora a la conclusión de Tarski. Éste planteó si habría alguna forma de expresar, en TNT, el concepto de verdad teórico-numérica. Ya hemos visto que la teoremidad es expresable (aunque no representable); Tarski estaba interesado en la cuestión análoga relativa a la noción de verdad. Más específicamente, quería determinar si existe alguna fórmula de TNT con una sola variable libre a, que pudiese ser traducida así:

“La fórmula cuyo número Gödel es a expresa una verdad”.

Supongamos, junto con Tarski, que sí existe una fórmula semejante, a la cual abreviaremos como VERDAD {a}. Ahora bien, lo que haremos será utilizar el método diagonalizador para producir un enunciado que afirme, acerca de sí mismo, que es una no verdad. Reproduciremos con exactitud el método Gödel, comenzando con un “tío”:

∃a:<~VERDAD{a}∧ARITMOQUINEREAR{a″,a}>

Digamos que el número Gödel del tío es t. Aritmoquinereamos este mismo tío, para producir la fórmula Tarski T:

Cuando es interpretado, esto nos dice:

“La aritmoquinificación de t es el número Gödel de un enunciado falso”.

Pero como la aritmoquinificación de t es el propio número Gödel de T, la fórmula T de Tarski reproduce, con toda exactitud, la paradoja de Epiménides dentro de TNT, diciendo de sí misma: “Soy una falsedad”. Por supuesto, esto conduce a la conclusión de que dicha fórmula debe ser, simultáneamente, verdadera y falsa (o, simultáneamente, ninguna de ambas cosas). Allí surge ahora una interrogación interesante: ¿Qué tiene de malo reproducir la paradoja de Epiménides? ¿Produce alguna consecuencia? Al fin y al cabo, ya lo hemos hecho en español, y el español no se ha evaporado.

La imposibilidad del Magnificangrejo

La respuesta demanda que se haga memoria de que aquí hay comprendidos dos niveles de significación. Uno es el que precisamente estamos usando; el otro es del tipo de los enunciados de teoría de los números. Si la fórmula T de Tarski realmente existiera, ¡habría entonces un enunciado relativo a números naturales que sería a la vez verdadero y falso! Éste es el obstáculo. Mientras que siempre no es posible esconder bajo la alfombra la paradoja de Epiménides en su formulación idiomática, diciendo que su contenido (su verdad) es abstracto, ¡ya no es así cuando la paradoja se convierte en un enunciado concreto referente a números! Si nos llega a parecer que ésta es una situación ridícula, tenemos por lo tanto que suprimir nuestra suposición de que existe la fórmula VERDAD {a}. Luego, no hay forma de expresar la noción de verdad en TNT. Tómese nota de que esto hace de la verdad una propiedad considerablemente más elusiva que la de teoremidad, pues esta última es expresable. Las mismas razones que tuvimos antes para rehacer nuestros pasos (con relación a la Tesis Church-Turing, Versión IA) nos conducen ahora a la conclusión de que:

La mente del Cangrejo no puede ser más reconocedora-de-la-verdad que un teorema-TNT-reconocedor.

Lo primero transgredería el Teorema Tarski-Church-Turing (“No hay procedimiento de decisión para la verdad aritmética”), en tanto que lo segundo transgredería el Teorema de Church.

Dos tipos de forma

Resulta sumamente interesante, por lo tanto, examinar la significación de la palabra “forma” cuando ésta se aplica a la interpretación de configuraciones arbitrariamente complejas. Pongamos por caso, ¿qué nos hace reaccionar cuando observamos una pintura y sentimos su belleza? ¿La “forma” de las líneas y puntos en nuestra retina? Evidentemente, debe ser eso, pues así es como examinan a aquélla nuestros mecanismos mentales de análisis; empero, la complejidad del procesamiento nos hace sentir que no estamos observando meramente una superficie bidimensional: estamos respondiendo a algún género de significación interior de la pintura, un elemento multidimensional aprisionado, de alguna manera, dentro de esas dos dimensiones. Lo importante aquí es la palabra “significación”; nuestras mentes contienen intérpretes que reciben los moldes bidimensionales y a continuación “extraen” de ellos nociones de elevada dimensionalidad, tan complejas que no podemos describirlas conscientemente. Viene al caso señalar que lo mismo puede decirse a propósito de cómo reaccionamos ante la música.

Subjetivamente, se percibe que los mecanismos de extracción de la significación interior carecen por completo de parentesco con los procedimientos de decisión que verifican la presencia o ausencia de una cualidad específica, como por ejemplo el carácter de bien formada de una cadena. Tal vez sea por ello que la significación interior sea algo que descubre más cosas de sí misma a medida que pasa el tiempo. A este respecto jamás se puede estar seguro, al modo en que sí es posible estarlo a propósito de lo bien formado, de que uno ha finiquitado el tema.

Esto nos propone la posibilidad de trazar una distinción entre los dos sentidos de “forma” de las pautas que hemos comentado. Primero, tenemos cualidades tales como la de bien formado, las cuales pueden ser aprehendidas mediante verificaciones predicablemente finalizables, igual que en los programas BuD. Propongo llamar a éstas las cualidades sintácticas de la forma: uno percibe, intuitivamente, que los atributos sintácticos de la forma reposan en un sitio muy cercano a la superficie y que, en concurrencia, no generan la creación de estructuras cognoscitivas multidimensionales.

En cambio, los aspectos semánticos de la forma son aquellos que no pueden ser verificados dentro de un lapso predictible: requieren verificaciones de finalización imprevisible. La teoremidad de las cadenas de TNT, como hemos visto, es un aspecto de esta clase; no se puede aplicar una verificación corriente a una cadena y determinar si es un teorema: de algún modo, el hecho de que esté involucrada su significación se relaciona crucialmente con la dificultad de establecer si una cadena es o no un teorema de TNT. El acto de extraer la significación de una cadena implica, en esencia, establecer los alcances de todas sus conexiones con todas las cadenas restantes, y ello inicia, sin la menor duda, un recorrido de finalización inagotable. Por lo tanto, las propiedades “semánticas” están vinculadas con búsquedas no finalizables ya que, en un sentido importante, la significación de un objeto no está situada en el objeto mismo. Esto no equivale a sostener que no es posible captar la significación de ningún objeto hasta el fin de los tiempos, pues a medida que el tiempo pasa la significación se va manifestando más y más. Con todo siempre quedan aspectos de aquella que siguen ocultos durante lapsos no previsibles.

La significación se deriva de conexiones con las estructuras cognoscitivas

Deslicémonos desde las cadenas de las composiciones musicales, sólo para variar. Si se lo prefiere, no obstante, se puede sustituir cualquier referencia a una pieza musical por el término “cadena”. Estas reflexiones pretenden ser genéricas, pero presiento que su espíritu ha de ser mejor comprendido mediante el auxilio de alusiones musicales.

La significación de una obra musical es curiosamente dual: por un lado, pareciera estar diseminada en todas partes, en virtud de su relación con muchas otras cosas del mundo; sin embargo, por otro lado, dicha significación se deriva, obviamente, de la música misma, de manera que es en alguna parte interior de esta última que ha de ser localizada.

La resolución de esta incógnita se produce cuando se toma en cuenta al intérprete: el mecanismo que efectúa la extracción de la significación. (En este contexto, por “intérprete” no quiero dar a entender el ejecutante de la composición, sino los mecanismos mentales de los cuales deriva la significación, en el oyente, cuando aquélla es ejecutada). El intérprete puede descubrir muchas facetas importantes del significado de una pieza cuando la escucha por vez primera, lo cual parecería confirmar la noción de que la significación se alberga en la pieza misma, y que simplemente es cuestión de descifrarla allí. Pero esto constituye sólo una parte de la historia. El intérprete musical actúa tendiendo una estructura cognoscitiva multidimensional, una representación mental de la composición, a la que trata de integrar con informaciones preexistentes mediante el hallazgo de vinculaciones con otras estructuras multidimensionales, las cuales codifican experiencias anteriores. Cuando este proceso tiene lugar, toda la significación, paulatinamente, se va manifestando. En realidad, pueden pasar años antes de que alguien sienta que ha penetrado en la significación central de una obra. Esto se insinuaría como un argumento en favor del punto de vista opuesto, el de que la significación está diseminada y que la función del intérprete consiste en ensamblarla, de manera paulatina.

Indudablemente, la verdad se encuentra en algún punto intermedio: las significaciones —sean musicales o lingüísticas— están, en cierta medida, localizadas y, también en cierta medida, diseminadas. Utilizando la terminología del Capítulo VI, podemos decir que las composiciones musicales y los textos son en parte desencadenadores y en parte transportadores de significación explícita. Una ilustración clara de este dualismo de la significación la provee el ejemplo de una tableta con una inscripción antigua: la significación de ésta se encuentra, en parte, almacenada en el cerebro de los especialistas y en las bibliotecas de todo el mundo; en parte, también, es obvio que está implícita en la tableta misma.

Así, otra manera de caracterizar la diferencia entre propiedades “sintácticas” y “semánticas” (dentro de los límites del sentido propuesto) es la observación de que las primeras residen inequívocamente dentro del objeto bajo examen, en tanto que las segundas dependen de sus relaciones con una clase potencialmente infinita de otros objetos: en consecuencia, no se las puede localizar en forma nítida. En principio, no hay ningún elemento críptico u oculto en las propiedades sintácticas; en cambio, la esencia de las propiedades semánticas es lo recóndito. Por esta razón es que propuse la distinción entre aspectos “sintácticos” y “semánticos” de la forma visual.

Belleza, verdad y forma

¿Qué diremos de la belleza? No se trata de una propiedad sintáctica, sin duda, de acuerdo a los conceptos expresados. ¿Es una plena propiedad semántica? ¿La belleza es una propiedad de la que está dotada, por ejemplo, una determinada pintura? Vamos a circunscribir nuestras consideraciones al caso de un observador individual: cualquiera ha tenido la experiencia de encontrar que una cosa es bella en una ocasión, insulsa en otra, y algo intermedio en otras oportunidades. Luego, ¿la belleza es un atributo que se modifica con el transcurso del tiempo? El esquema puede ser invertido y decirse que quien varia es el contemplador. Dado un contemplador determinado de una pintura determinada en un momento determinado, ¿es legítimo afirmar que la belleza es una cualidad definitivamente presente o ausente?

Es probable que, en cada persona, se movilicen diferentes niveles de intérpretes, según las circunstancias. Estos diversos intérpretes extraen diferentes significaciones, establecen diferentes conexiones y, por lo común, hacen una evaluación de los aspectos profundos en forma completamente diferente. Pareciera, pues, que esta noción de belleza es sumamente difícil de fijar. Por esta razón es que opté por vincular a la belleza, en el Magnificangrejo, con la verdad, la cual, como hemos palpado, es por su parte una de las nociones más inasibles de la metamatemática.

El sustrato neural de la paradoja de Epiménides

Querría finalizar este capítulo incluyendo algunas reflexiones sobre el problema central de la verdad: la paradoja de Epiménides. Creo que la reproducción, por Tarski, de la paradoja de Epiménides en el interior de TNT, señala el camino hacia una comprensión más profunda de la paradoja en el ámbito idiomático. Lo que Tarski descubre es que esta versión de la paradoja tiene dos niveles distintos. En un nivel, es un enunciado a propósito de sí mismo que sería verdadero si fuese falso, y falso si fuese verdadero. En el otro nivel —que prefiero llamar sustrato aritmético— es un enunciado a propósito de los enteros que es verdadero si, y sólo si, es falso.

Ahora bien, por algún motivo, este último perturba a la gente muchísimo más que el primero. Hay quienes, sencillamente, desestiman al primero como “carente de significado”, a causa de su autorreferencialidad. Pero no se puede desestimar un enunciado paradójico referido a los enteros; los enunciados referidos a enteros no pueden ser al mismo tiempo verdaderos y falsos.

Mi impresión es que la transformación tarskiana de la paradoja de Epiménides nos induce a buscar un sustrato en la versión idiomática. En la versión aritmética, el nivel superior de significación se sustenta en el nivel aritmético inferior. Tal vez análogamente, la oración autorreferencial que percibimos (“Este enunciado es falso”) sea nada más que el nivel máximo de una entidad compuesta por dos niveles. ¿Cuál sería, entonces, el nivel inferior? Bueno, ¿sobre qué mecanismo va montado el lenguaje? El cerebro. Por lo tanto, se debe buscar el sustrato neural de la paradoja de Epiménides: un nivel más bajo, donde encontramos acontecimientos físicos chocando entre sí. Es decir, dos acontecimientos que, por su naturaleza, no pueden ocurrir simultáneamente. Si existe este sustrato físico, la razón por la cual no podemos hallarle pies ni cabeza al enunciado de Epiménides es que nuestros cerebros están tratando de complementar una tarea imposible.

¿Y cuál sería la naturaleza de los acontecimientos físicos en colisión? Presumiblemente, cuando escuchamos el enunciado de Epiménides, nuestro cerebro traza alguna “codificación” del mismo: una configuración interna de símbolos en interacción. Luego, trata de clasificar el enunciado como “verdadero” o como “falso”; este acto clasificador tiene que implicar un esfuerzo por obligar a diversos símbolos a interactuar de una manera específica. (Quizá suceda así con el procesamiento de cualquier enunciado). Pero si sucede que el acto de clasificación desbarata la codificación del enunciado —cosa que, de ordinario, jamás ocurre— nos sentimos en apuros, pues esta situación equivale a tratar de obligar a un fonógrafo a ejecutar el disco preparado para destruirlo. Acabamos de describir el conflicto en términos físicos, pero no en términos neurales. Si hasta aquí hemos analizado correctamente, es posible, entonces, que la discusión pendiente pueda tener lugar cuando sepamos algo sobre la constitución de los “símbolos” que se opera en el cerebro a partir de las neuronas y sus excitaciones, y sobre la forma en que los enunciados se convierten en “codificaciones”.

Este esbozo relativo al sustrato neural de la paradoja de Epiménides sugiere (a mí, por lo menos) que la resolución de la versión idiomática de la paradoja podría ser similar a la resolución de la versión Tarski. Tal resolución involucra el abandono de la noción de que el cerebro puede aportar una representación totalmente rigurosa del concepto de verdad. Lo novedoso de esto reside en su sugerencia de que es imposible, por razones enteramente físicas, un modelamiento cabal de la verdad: específicamente, este modelamiento requeriría que en el cerebro se produzcan acontecimientos que, desde el punto de vista físico, son incompatibles entre sí.