CAPÍTULO V
Estructuras y procesos recursivos
¿Qué es la recursividad?
¿QUE ES LA RECURSIVIDAD? Es lo que ha sido ilustrado por el Diálogo anterior, el Pequeño laberinto armónico: incrustaciones y variaciones de incrustaciones. El concepto es muy amplio (relatos dentro de relatos, películas dentro de películas, muñecas rusas dentro de muñecas rusas (o comentarios entre paréntesis dentro de comentarios entre paréntesis), son solamente algunos de los encantos de la recursividad). Sin embargo, debe tenerse en cuenta que la significación de “recursivo” en este capítulo tiene únicamente una relación lejana con lo dicho al respecto en el Capítulo III. Aclararemos el tema al final de este capítulo.
A veces, la recursividad parece aproximarse mucho a la paradoja. Por ejemplo, las definiciones recursivas, las cuales pueden dar la impresión de que se está definiendo algo en función de ello mismo. Esto implicaría una circularidad, y conduciría a una regresión infinita, si no a la paradoja misma. En verdad, una definición recursiva (si es adecuadamente formulada) jamás conduce a una regresión infinita ni a una paradoja. Y es así porque una definición recursiva nunca define una cosa en función de esa cosa sino, siempre, en función de las interpretaciones más simples de la misma. Enseguida se aclarará qué quiero decir con esto, a través de algunos ejemplos.
Una de las formas más comunes bajo las cuales aparece la recursividad en la vida cotidiana es cuando se posterga la finalización de una tarea, con el objeto de ocuparse de otra más sencilla, a menudo del mismo género. Veamos: un ejecutivo cuenta con un aparato telefónico muy versátil, por el que recibe muchas llamadas. Está hablando con A, y es llamado por B; dice entonces a A, “¿tendría inconveniente en esperar un momento?”. Por supuesto que en realidad no le preocupa si A tiene inconveniente o no; aprieta un botón, y se pone en comunicación con B. Ahora es C quien llama, y la conversación con B queda en suspenso. Esto podría extenderse indefinidamente, pero no nos vamos a dejar llevar por el entusiasmo. Digamos entonces que la comunicación con C finaliza; nuestro ejecutivo, pues, se “saca” de vuelta para arriba hasta B, y continúa su conversación con él. En tanto, A sigue sentado al otro extremo de la línea, haciendo tamborilear sus uñas sobre la superficie de algún escritorio, y probablemente escuchando espantosa música funcional que la línea telefónica le transmite para aplacarlo… La alternativa más sencilla sería que la comunicación con B termine y el ejecutivo reanude finalmente su conversación con A. Pero podría suceder que, después de continuar la comunicación con B, haya una nueva llamada, ahora de D. En tal caso, B sería otra vez puesto en la pila de los que esperan y sería atendido D. Este ejecutivo se comporta en forma irremediablemente mecánica, sin duda, pero nos permite ilustrar la recursividad de manera muy precisa.
Meter, sacar y pilas
En el ejemplo anterior, hemos utilizado cierta terminología básica de la recursividad, por lo menos tal como la consideran los especialistas en computación. Se trata de los términos meter, sacar y pila, los cuales están todos relacionados entre sí. Fueron introducidos a fines de los años cincuenta como parte del IPL, uno de los primeros lenguajes de Inteligencia Artificial. Ya hemos tropezado con “meter” y “sacar” en el Diálogo. Pero vamos a extendernos algo más sobre estos conceptos. Meter significa suspender las operaciones relativas a la tarea que se tiene entre manos, sin olvidar el punto en que se está, y emprender otra tarea. De esta última se dice, usualmente, que está ubicada “en un nivel más bajo” que la anterior. Sacar significa lo opuesto: completar las operaciones correspondientes al primer nivel, reasumiéndolas en el punto exacto donde fueron suspendidas, y ascendiendo para ello un nivel.
Ahora bien, ¿cómo recordar con precisión en qué punto se estaba en cada diferente nivel? La respuesta es: mediante el almacenamiento de la información pertinente en una pila. En consecuencia, una pila es un tablero que nos indica cosas tales como, 1) dónde quedó suspendida cada tarea no terminada (dirección de retomo, en la jerga técnica); 2) cuáles son los hechos que deben ser conocidos a propósito del punto de interrupción (enlaces variables, en la misma jerga). Cuando uno se saca de vuelta hacia arriba para reasumir una tarea, la pila se encarga de restablecer el contexto correspondiente, eliminando toda confusión u olvido posibles. En el ejemplo de las llamadas telefónicas, la pila nos dice quién está esperando en cada uno de los diferentes niveles, y dónde estábamos al interrumpirse la conversación.
Digamos al margen que los términos “meter” “sacar” y “pila” han sido sugeridos por la observación de la pila de bandejas de una cafetería: por lo general, se produce cierta clase de empuje desde abajo, que tiende a mantener la bandeja más alta a una altura relativamente constante; cuando se mete una bandeja sobre la pila, esta última se hunde un poco, y cuando se saca una bandeja, la pila se estira hacia arriba, también un poco.
Otro ejemplo extraído de la vida diaria: los programas radiofónicos de noticias, a veces, desplazan la emisión de información hacia algún corresponsal extranjero; así “ahora escucharemos a Jorge Lamadrid desde Valparaíso, Chile”. Allá, Lamadrid obtiene la grabación de una entrevista mantenida por un periodista local con determinada persona y entonces, después de reseñar brevemente la situación, hace escuchar la cinta magnetofónica: “Con ustedes, quien les habla, Eduardo Castro, directamente desde el escenario de los hechos, en las afueras de Valparaíso, donde tuvo lugar el espectacular asalto. Voy a dialogar a continuación con el señor…”. A esta altura, el oyente está tres niveles más abajo. Podría ocurrir que el entrevistado, a su vez, haga escuchar la grabación de alguna conversación anterior. No es demasiado insólito bajar tres niveles en estos programas y, curiosamente, es muy raro que tomemos conciencia de las suspensiones. El recorrido trazado, en cambio, es seguido por nuestro pensamiento subconsciente con entera facilidad, a causa quizá de que los diversos niveles difieren mucho entre sí en cuanto a su cualidad; si ésta fuera similar, nos confundiríamos de inmediato.
Un ejemplo de recursividad más compleja lo da, por supuesto, nuestro diálogo. Allí, Aquiles y la Tortuga aparecen en todos los niveles; en ocasiones, leen una historia de la que al mismo tiempo son personajes. Por ello, el lector puede sentirse algo inseguro con respecto a la ilación argumental, y le es necesaria una atenta concentración para mantener ordenados los elementos: “Veamos, los verdaderos Aquiles y la Tortuga permanecen allá arriba, en poder de Buenafortuna, pero los secundarios están dentro de un cuadro de Escher… y luego encontraron ese libro, y lo están leyendo, de manera que quienes vagan por los surcos del Pequeño Laberinto Armónico son la Tortuga y Aquiles terciarios. No, un momento, en alguna parte me pasé por alto un nivel…”. Para trazar el recorrido que sigue la recursividad en el Diálogo, es preciso contar con una pila mental, expresamente conformada, similar a la que presenta la figura 26.

FIGURA 26. Diagrama de la estructura del Diálogo Pequeño Laberinto Armónico. Los descensos verticales son metidas; los ascensos son sacadas. Adviértase la correspondencia de este diagrama con la disposición de los márgenes tipográficos en el Diálogo. El diagrama pone en claro que la tensión inicial —la amenaza de Buenafortuna— quedará sin resolver; Aquiles y la Tortuga permanecen suspendidos en el cielo. Algunos lectores se preocuparán enormemente ante esta metida no sacada, mientras que otros no se inquietarán en absoluto. En la narración, también el laberinto musical de Bach es interrumpido prematuramente. Aquiles, sin embargo, no se percata para nada de la existencia de algo extraño; únicamente la Tortuga percibe la tensión más global que sigue pendiente.
Pilas y música
Cuando comentemos el Pequeño Laberinto Armónico, será preciso hablar expresamente de algo que fue sugerido en el Diálogo, sin enunciarlo explícitamente, a saber: que escuchamos música de modo recursivo; específicamente, que elaboramos una pila mental de tonalidades y que cada nueva modulación mete una nueva tonalidad en la pila. Como resultado, también ahora, deseamos escuchar esa secuencia de tonalidades en orden inverso al de su apilamiento, es decir sacar una a una las tonalidades metidas, hasta llegar a la tónica. Lo anterior es una exageración, pero encierra un grano de verdad.
Cualquier persona medianamente afecta a la música construye, en forma instintiva, una pila rudimentaria formada por dos tonalidades. En esta “pila reducida” son conservadas la auténtica tónica y la “seudotónica” más cercana (la que el compositor simula querer alcanzar); en otras palabras, la tonalidad más global y la más particular. De tal modo, ese oyente sabe cuándo ha sido recuperada la tónica verdadera y experimenta una profunda sensación de “aligeramiento”. Ese oyente también puede distinguir (a diferencia de Aquiles) entre un alivio localizado de la tensión —una resolución dentro de la seudotónica, por ejemplo— y una resolución global, en lugar de aligerarla, pues se trata de un acto irónico, idéntico al rescate de Aquiles cuando colgaba peligrosamente, aferrado a la oscilante lámpara, en tanto el lector sabía que él y la Tortuga, por cierto, aguardaban el cumplimiento de un funesto destino a manos de Monsieur Buenafortuna y su cuchillo.
Los ejemplos de estas situaciones son muy frecuentes en el campo de la música, puesto que el corazón y el alma de ésta son la tensión y la resolución. Pero nos limitaremos a observar un ensamblamiento de Bach, quien compuso numerosas piezas en la forma “AABB”, esto es, integradas por dos mitades, cada una de ellas repetida. Tomaremos la jiga de la Suite Francesa número 5, en un todo representativa de la forma citada; su nota tónica es sol, establecida vigorosamente por una alegre melodía de danza. Pronto, no obstante, una modulación en la sección A conduce al tono, estrechamente relacionado, de re (la dominante). Cuando acaba la sección A, estamos en la tonalidad de re. ¡En realidad, da la impresión de que la pieza ha terminado en esa tonalidad! (O, por lo menos, es la impresión que recogería Aquiles). Pero entonces ocurre algo extraño: retomamos de un brinco al comienzo, con sol por tónica, y volvemos a escuchar idéntica transición a re. Pero entonces ocurre algo extraño: retornamos de un brinco al comienzo, con sol por tónica, y volvemos a escuchar idéntica transición a re.
A continuación viene la sección B. Con el desplazamiento temático producido, empezamos en re como si ésta hubiera sido siempre la tónica, pero modulamos retornando a sol, después de todo, lo cual significa que nos sacamos de vuelta a la tónica, y así termina la sección B, adecuadamente. Entonces, reaparece la curiosa repetición, arrojándonos sin aviso previo en re, y permitiéndonos luego retomar a sol una vez más. Entonces, reaparece la curiosa repetición, arrojándonos sin aviso previo en re, y permitiéndonos luego retomar a sol una vez más.
El efecto psicológico de todos estos cambios de tónica —bruscos unos, suaves otros— es muy difícil de describir. Es parte de la magia de la música el hecho de que podamos, instintivamente, encontrarle sentido a estos cambios. O quizá es la magia de Bach el haber podido componer obras con esta clase de estructura, dotándolas de tal graciosa naturalidad que no sabemos con exactitud qué es lo que está sucediendo.
El Pequeño Laberinto Armónico original es una pieza donde Bach trata de extraviar al oyente en un laberinto de súbitos cambios de tonalidad. Muy pronto, lo desorienta hasta enajenarle todo sentido de ubicación: ya no sabe cuál es la verdadera tónica, salvo que tenga el don de una captación perfecta o que, como Teseo, goce de la amistad de una Ariadna que lo provea de un hilo salvador.
En este caso, empero, en lugar de un hilo se requiere de una partitura escrita. Esta obra —otro ejemplo es el Canon Eternamente Remontante— nos viene a mostrar que, en tanto oyentes de música, carecemos de pilas cuyo trazado se ahonde lo suficiente y que sean verdaderamente confiables.
La recursividad en el lenguaje
Posiblemente tengamos una capacidad de apilamiento mental mucho más grande con relación al lenguaje. La estructura gramatical de todos los idiomas implica la elaboración perfectamente organizada de pilas. Sin embargo, no hay duda de que la dificultad para comprender una oración determinada se incrementa notoriamente con la cantidad de metidas sobre la pila que se produzcan. El mentado fenómeno del “verbo-al-final” en el idioma alemán, acerca del cual se cuentan cómicas anécdotas sobre distraídos profesores que inician una frase, pasan a disquisiciones que los ocupan por el lapso de toda una conferencia, y luego finalizan acumulando a la carrera una retahíla de verbos que a su audiencia, cuya pila ya hacía tiempo había dejado de mantener coherencia, dejan perpleja, es una muestra excelente de metidas y sacadas lingüísticas. La confusión que, en la audiencia que saca desordenadamente, echando mano a la pila coronada por los verbos del profesor, es fácil y divertida de imaginar, puede engendrarse. Pero en el alemán hablado de todos los días, tales pilas profundas casi nunca se producen; por cierto, los hablantes nativos de este idioma transgreden determinadas convenciones, que exigen la ubicación final del verbo, a fin de evitar el esfuerzo mental de retener el recorrido trazado por la pila. Todos los idiomas tienen construcciones que implican pilas, claro que, por lo general, de naturaleza menos espectacular que el alemán. Con todo, siempre hay modos de reformular las frases, de modo tal que la profundidad de apilamiento se reduzca al mínimo.
Redes de transición recursiva
La estructura sintáctica de la oración facilita el enunciado de un método para describir estructuras y procesos recursivos: el de la Red de Transición Recursiva (RTR). Una RTR es un diagrama que muestra diversos caminos que pueden ser seguidos para realizar una tarea determinada. Cada camino consiste en varios nódulos, o pequeños recuadros que encierran palabras, vinculados entre sí mediante arcos, o sea líneas que incluyen flechas direccionales. La denominación global de la RTR se escribe a la izquierda, separadamente, y el primero y último nódulo contienen, en forma respectiva, las palabras comienzo y final. Los demás nódulos contienen instrucciones muy breves y explícitas que cumplir, o bien denominaciones de otras RTR. Cada vez que aparece un nódulo, se deben obedecer sus instrucciones o, en su caso, brincar a la RTR nombrada en él, y desarrollarla.

FIGURA 27. Red de Transición Recursiva de NOMBRE MODIFICADO y NOMBRE ULTRAMODIFICADO.
Tomemos como muestra una RTR denominada NOMBRE MODIFICADO, que nos dice cómo construir una frase nominal (véase figura 27a). Si recorremos NOMBRE MODIFICADO paso a paso, en forma puntualmente horizontal, comenzamos, después producimos un ARTÍCULO, un NOMBRE, y los ADJETIVOS que sean convenientes, antes y/o después del NOMBRE, y luego finalizamos. Por ejemplo, “el jabón tontuelo”, o “un refrigerio desagradecido”. Pero hay otras posibilidades, señaladas por los arcos, tales como dejar de lado el artículo, o sumar adjetivos; podemos construir así “leche”, o bien “mayúsculos estornudos verdes, azules, rojos, etc.”.
Cuando uno llega al nódulo NOMBRE, le pide a la ignota caja negra llamada NOMBRE que le seleccione un nombre o sustantivo de entre los que tiene almacenados. En la terminología de la computación esto se conoce como “solicitud de procedimiento”, e implica que en forma temporaria se le otorga el control de la tarea a procedimiento (NOMBRE, aquí), el cual, 1) realiza su tarea (produce un nombre), y luego, 2) devuelve el control. En la RTR anterior, se solicitan estos procedimientos: ARTÍCULO, NOMBRE y ADJETIVO. Ahora bien, la RTR NOMBRE MODIFICADO puede, al ser requerida, salir de otra RTR, por ejemplo de una RTR llamada ORACIÓN. En este caso, NOMBRE MODIFICADO produciría una frase nominal como la de “el jabón tontuelo”, y luego volvería a su lugar, dentro de ORACIÓN, desde el cual había sido solicitada. Esto es enteramente análogo al modo en que se reasume el vínculo, a partir del punto donde se lo había suspendido, en el caso de las llamadas telefónicas encastradas unas en otras, o de las emisiones periodísticas radiofónicas, también metidas unas dentro de otras.
Sin embargo, a pesar de que esto se llama “red de transición recursiva”, no hemos exhibido hasta ahora ninguna verdadera recursividad.
Las cosas se hacen recursivas —y circulares, en apariencia— cuando se aborda una RTR como la de la figura 27b, correspondiente a NOMBRE ULTRAMODIFICADO. Está a la vista que todo camino posible en NOMBRE ULTRAMODIFICADO implica una apelación a NOMBRE MODIFICADO, de modo que es imposible evitar la presencia de nombres de una u otra clase. También es posible llegar a este grado de modificación sólo con enunciar “leche” o “mayúsculos estornudos verdes, azules, rojos”, pero tres de los recorridos incluyen llamadas recursivas a NOMBRE ULTRAMODIFICADO mismo. Sin duda, pareciera que se estuviese definiendo algo en función de sí mismo.
La respuesta es “sí, pero benignamente”. Supongamos que en el procedimiento ORACIÓN hay un nódulo que pide NOMBRE ULTRAMODIFICADO. Esto significa que, al afrontarlo, tenemos que encomendar a nuestra memoria (es decir, a la pila) la ubicación de este nódulo dentro de ORACIÓN, para saber adónde debemos retornar, y luego dedicar nuestra atención al procedimiento NOMBRE ULTRAMODIFICADO. Por ende, tenemos que elegir un camino que nos permita generar un NOMBRE ULTRAMODIFICADO. Sigamos, por ejemplo, el camino más bajo de los dos superiores, cuya secuencia es:
NOMBRE MODIFICADO; PRONOMBRE RELATIVO; NOMBRE ULTRAMODIFICADO; VERBO.
En consecuencia, lanzamos un NOMBRE MODIFICADO: “las aromáticas empanadas gallegas”, un PRONOMBRE RELATIVO: “que”; y en el momento siguiente nos preguntamos por un NOMBRE ULTRAMODIFICADO, ¡pero estamos en medio de un NOMBRE ULTRAMODIFICADO! Sí, y sin embargo recordemos a nuestro ejecutivo, quien se encontraba en medio de una comunicación telefónica en el momento de ser requerido por otra comunicación telefónica, y resolvía la situación almacenando el estado vigente de la comunicación inicia) en una pila, y comenzando la subsiguiente como si no ocurriese nada inusual. Actuaremos, pues, de forma similar.
Primero, anotamos en nuestra pila el nódulo en que nos encontramos al toparnos con NOMBRE ULTRAMODIFICADO, a fin de contar con una “dirección de retomo”; luego, brincamos sin más preámbulo al comienzo de NOMBRE ULTRAMODIFICADO, como si no sucediese nada inusual. Ahora también tenemos que elegir un camino. Para variar, optamos por el más bajo del diagrama:
NOMBRE MODIFICADO; PREPOSICIÓN; NOMBRE ULTRAMODIFICADO
Entonces, debemos producir un NOMBRE MODIFICADO (digamos, “la vaca violeta”), después una PREPOSICIÓN (digamos, “sin”), y a continuación tropezamos otra vez con la recursividad. Así que nos sujetamos bien el sombrero y descendemos otro nivel. Para obviar complejidades, supongamos que el camino elegido ahora es el directo: únicamente NOMBRE MODIFICADO, y lo llenamos con, por ejemplo, “cuernos”; encontramos después el nódulo final de este procedimiento, indicativo de que salimos del mismo: nos dirigimos pues a nuestra pila para encontrar la dirección de retomo. Ésta nos dice que estábamos en la mitad de la ejecución de NOMBRE ULTRAMODIFICADO en un nivel más alto, así que debemos proseguir desde este punto. El NOMBRE ULTRAMODIFICADO producido aquí es “la vaca violeta sin cuernos”, y en este nivel nos topamos otra vez con final, por lo que también lo abandonamos, y luego somos remitidos a un punto donde se nos requiere un VERBO —optamos por “engulló”— y así completamos la solicitud de NOMBRE ULTRAMODIFICADO de más alto nivel, con el siguiente resultado:
“las aromáticas empanadas gallegas que la vaca violeta sin cuernos engulló”.
Cuando más sacamos por última vez de los trazados que muestra el diagrama, es para ascender hasta la paciente ORACIÓN, a la cual incorporamos la frase obtenida.
Como se ve, no se ha caído en una situación de regresión infinita; la razón está en que por lo menos uno de los caminos de la RTR NOMBRE ULTRAMODIFICADO no incluye ninguna llamada recursiva a NOMBRE ULTRAMODIFICADO mismo. Por supuesto, podríamos haber insistido perseverantemente en elegir siempre el camino inferior del diagrama, caso en el cual la tarea no habría tenido fin, tal como ocurre con la sigla “DIOS”, cuya expansión nunca puede llegar a un nivel definitivo. Pero si los recorridos se eligen al azar, no ingresamos en situaciones de regresión infinita.
“Saneamiento” y heterarquía
El mencionado es el hecho fundamental que distingue las definiciones recursivas de las circulares. Siempre hay alguna parte de la definición que evita la autorreferencia, de modo que, en último término, la acción de construir un objeto que satisfaga la definición terminará por “sanearse”.
Ahora bien, hay otros métodos, más indirectos que los de autoapelación, para generar recursividad en RTR. Existe uno, análogo al utilizado por Escher en Manos dibujando (figura 135), donde cada uno de los dos procedimientos apela al otro, pero no a sí mismo. Por ejemplo, podemos tener una RTR llamada CLAUSULA, la cual pide NOMBRE ULTRAMODIFICADO siempre que un verbo transitivo necesita un objeto y, recíprocamente, el recorrido superior de NOMBRE ULTRAMODIFICADO pediría PRONOMBRE RELATIVO y luego CLAUSULA, cuando tenga necesidad de una cláusula relativa. Esto ejemplifica una recursividad indirecta, y es análogo también a la versión de la paradoja de Epiménides que moviliza dos recorridos enfrentados.
No hace falta señalar que puede haber un terceto de procedimientos que no se requieran entre sí, cíclicamente y por siempre. Puede haber asimismo un grupo entero de distintas RTR que se imbriquen recíprocamente, apelando cada una de ellas a sí mismas y a todas las otras en forma intensa. Un programa dotado de semejante estructura, donde no exista un “nivel superior” único, o “monitor”, es una heterarquía (por oposición a jerarquía). El término ha sido acuñado, según creo, por Warren McCulloch, uno de los primeros cibernetistas y un profundo estudioso de la inteligencia y del pensamiento.
Expansión de nódulos
Un método gráfico de concepción de la RTR es el que sigue. Cada vez que, al seguir un camino, se encuentra un nódulo que pide una RTR, uno “expande” ese nódulo, lo cual significa sustituirlo por una reproducción, en pequeña escala, de la RTR solicitada (véase figura 28). ¡A continuación, se trabaja en el interior de la RTR reducida!

FIGURA 28. La RTR NOMBRE ULTRAMODIFICADO, con un nódulo expandido recursivamente.
Cuando uno se saca de aquél, automáticamente se está en el lugar adecuado, dentro del diagrama mayor. A la vez, mientras se permanece en el reducido, es posible abocarse a la construcción de miniaturas aún más pequeñas de RTR. Pero basta con expandir los nódulos que se van encontrando para evitar la necesidad de diseñar un diagrama infinito, inclusive cuando una RTR apela a sí misma.
Expandir un nódulo se parece un tanto a la tarea de reemplazar una letra, dentro de una sigla, por la palabra que esa letra representa. La sigla “DIOS” es recursiva, pero presenta el defecto —o la ventaja— de que la ‘D’ tiene que ser sucesivamente expandida: en consecuencia, nunca se sanea. Por ello, cuando se instrumenta una RTR como programa real de computación, siempre existe por lo menos un recorrido que elude la recursividad (directa o indirecta), a fin de no crear una situación de infinita regresión. Los programas más heterárquicos consiguen sanearse o no podrían funcionar, pues consistirían en la expansión sucesiva de un nódulo tras otro, sin completar jamás acción alguna.
Diagrama D y secuencias recursivas
Infinitas estructuras geométricas pueden ser definidas exactamente de ese modo, a través de la expansión de un nódulo tras otro. Por ejemplo, vamos a definir un diagrama infinito denominado “Diagrama D”. Para ello, utilizaremos un método implícito de representación. Nos limitaremos a escribir en dos nódulos la letra ‘D’ la cual, sin embargo, estará representando una reproducción completa del Diagrama D. En la figura 29a, el Diagrama D es presentado implícitamente, pero si queremos observarlo más explícitamente, expandimos cada una de las dos D: es decir, las sustituimos por el mismo diagrama, sólo que en tamaño reducido (véase figura 29b). Esta “segunda” versión del Diagrama D nos permite sospechar cómo será el último, e imposible-de-completar, Diagrama D. La figura 30 exhibe una porción más amplia del Diagrama D, donde todos los nódulos han sido numerados desde la base, y de izquierda a derecha. Dos nódulos adicionales, numerados 1 y 2, han sido agregados en la base.
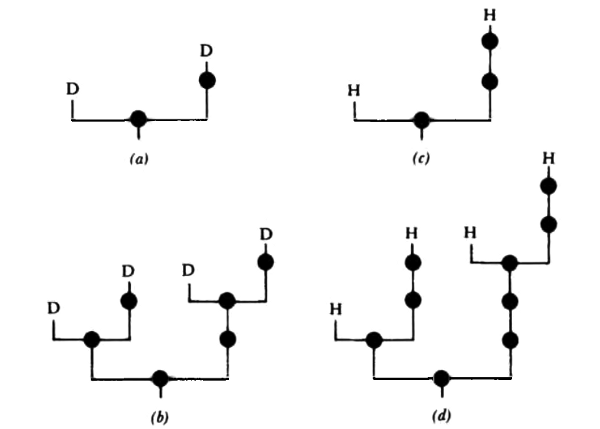
FIGURA 29. (a) Diagrama D, sin expandir. (b) Diagrama D, expandido una vez. (c) Diagrama H, sin expandir. (d) Diagrama H, expandido una vez.
Este árbol infinito tiene ciertas curiosísimas propiedades matemáticas. Subiendo por su borde derecho, encontramos la célebre secuencia de los números de Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Fue descubierta alrededor del año 1202 por Leonardo de Pisa, hijo de Bonaccio, llamado en consecuencia “Filius Bonacci” o, abreviadamente, “Fibonacci”. Estos números son mejor definidos, recursivamente, por el siguiente par de fórmulas:
FIBO(n) = FIBO(n − 1) + FIBO(n − 2) para n>2
FIBO(1) = FIBO(2) = 1

FIGURA 30. Diagrama D, con mayor expansión y nódulos numerados.
Adviértase cómo los sucesivos números de Fibonacci son definidos en función de los anteriores. Podemos representar este par de fórmulas a través de una RTR (figura 31).
Así, se puede calcular FIBO(15) mediante una secuencia de apelaciones recursivas al procedimiento definido por la RTR de la figura. Esta definición recursiva se sanea cuando uno se encuentra con FIBO(1) o FIBO(2), que son dados explícitamente, luego de haber ido hacia atrás, recorriendo los valores descendentes de n. Es un poco fastidioso marchar hacia atrás, cuando bien se podría ir hacia adelante, comenzando con FIBO(1) y FIBO(2), y sumando cada vez los dos valores inmediatamente anteriores, hasta alcanzar FIBO(15). De esta forma, no se necesita retener el trazado de una pila.

FIGURA 31. Una RTR de los números de Fibonacci.
Ahora bien, el Diagrama D presenta otras propiedades, más sorprendentes aún. Toda su estructura puede ser codificada por una sola definición recursiva, a saber:
D(n) = n − D(D(n − 1)) para n>0
D(0) = 0
¿Cómo hace la función D(n) para codificar la estructura de árbol del Diagrama? Muy sencillamente: si uno construye un árbol, colocando D(n) debajo de n, para todos los valores de n, recreará el Diagrama D. En verdad, así fue como yo descubrí el Diagrama D. Me encontraba investigando la función D y, como quería calcular rápidamente sus valores, se me ocurrió distribuir gráficamente los que ya conocía, mediante el auxilio de un árbol. Para mi sorpresa, éste manifestó esa capacidad geométrica de descripción, tan ordenadamente recursiva.
Aún más asombroso es que, si se elabora un árbol similar para una función H(n), definida con una autoinclusión más que D,
H(n) = n − H(H(H(n − 1))) para n>0
H(0) = 0,
su Diagrama asociado, el “Diagrama H”, tiene que ser definido como lo muestra la figura 29c. Su brazo derecho contiene un nódulo más, es la única diferencia. La primera expansión recursiva del Diagrama H es la que exhibe la figura 29d. Y a sí se mantiene, para cualquier grado de autoinclusión. Hay una atractiva regularidad en las estructuras geométricas recursivas, que se corresponde en forma precisa con la que exhiben las definiciones algebraicas recursivas.
Un problema para lectores inquietos: supongamos que se hace girar el Diagrama D como si lo reflejase un espejo, y se numeran los nódulos del nuevo árbol de modo que los valores aumenten de izquierda a derecha, ¿se podría encontrar una definición algebraica recursiva de este “árbol invertido”? ¿Y qué se podría decir acerca de una posible “inversión” del árbol H? ¿Etc.?
Otro ameno problema es el que plantean dos funciones enlazadas recursivamente, F(n) y M(n) —funciones “casadas” entre sí, podríamos decir— y así definidas:
} para n>0
F(n) = n − M(F(n − 1))
M(n) = n − F(M(n − 1))
F(0) = 1, y M(0) = 0
La RTR de cada una de estas funciones apela a la de la otra y también a sí misma. El problema consiste exclusivamente en descubrir las estructuras recursivas del Diagrama F y del Diagrama M: son muy simples y armoniosas.
Una secuencia caótica
Un último ejemplo de recursividad en teoría de los números nos lleva a un pequeño misterio. Consideremos la siguiente definición recursiva de una función:
Q(n) = Q(n−Q(n−1)) + Q(n−Q(n−2)) para n>2
Q(1) = Q(2) = 1
Esto recuerda la definición de Fibonacci en cuanto a que cada nuevo valor, acá, es la suma de dos valores anteriores. Pero no de los dos inmediatamente anteriores, que ahora pasan a indicarnos hasta dónde es necesario retroceder para obtener los números que, sumados, den lugar al valor siguiente… Los primeros 17 números Q son:

Para establecer el siguiente, es preciso correrse hacia la izquierda (desde los tres puntos suspensivos) 10 y 9 lugares, respectivamente; nos encontraremos así con un 5 y un 6, señalados por las flechas. Su suma —11— produce el nuevo valor: Q(18). Se trata de un raro proceso, mediante el cual la lista de números Q conocidos se utiliza a sí misma para extenderse. La secuencia que resulta es, para decirlo benévolamente, errática; cuanto más se la prolongue, menos sentido se le hallará. Éste es uno de esos casos muy singulares, donde lo que parece ser una definición más bien normal conduce a un comportamiento sumamente enigmático: un caos producido de manera muy ordenada. Uno tiende naturalmente a preguntarse si el aparente caos nos oculta alguna sutil regularidad. Por definición, hay regularidad, ciertamente, pero el interés reside en si existe otra forma de caracterizar esta secuencia y en que tengamos la suerte de que sea una forma no recursiva.
Dos sorprendentes gráficas recursivas
Los prodigios de la recursividad, dentro de la matemática, son incontables, y no tengo el propósito de presentarlos en su totalidad. Empero, hay una pareja de ejemplos particularmente llamativos, surgidos de mi experiencia, que creo merecen ser citados. Son gráficas: una apareció en el curso de ciertas investigaciones relativas a teoría de los números, la otra durante la elaboración de mi tesis doctoral sobre física de los estados sólidos. Lo fascinante, en realidad, es que las gráficas se relacionan entre sí en forma estrecha.
La primera (figura 32) es la gráfica de una función a la que llamo INT(x). Es representada aquí por x entre 0 y 1. Para x entre cualquier otro par de enteros n y n + 1, basta con encontrar INT(x − n) y luego sumarle n. La estructura del diseño es completamente saltarina, como se ve. Consiste en un número infinito de porciones curvadas, que se van haciendo más pequeñas hacia las esquinas, y al mismo tiempo menos curvadas cada vez. Ahora bien, si se observan atentamente dichas porciones, se descubrirá que cada una de ellas es, por cierto, ¡una reproducción de toda la gráfica, sólo que curvada! Las implicaciones que surgen son extravagantes: por ejemplo, que la gráfica de INT consiste exclusivamente en reproducciones de sí misma, autoincluidas hasta una profundidad infinita. Si uno selecciona cualquier porción de la gráfica, por pequeña que sea, tiene en ella una reproducción completa de la gráfica total, ¡en realidad, infinitas reproducciones!
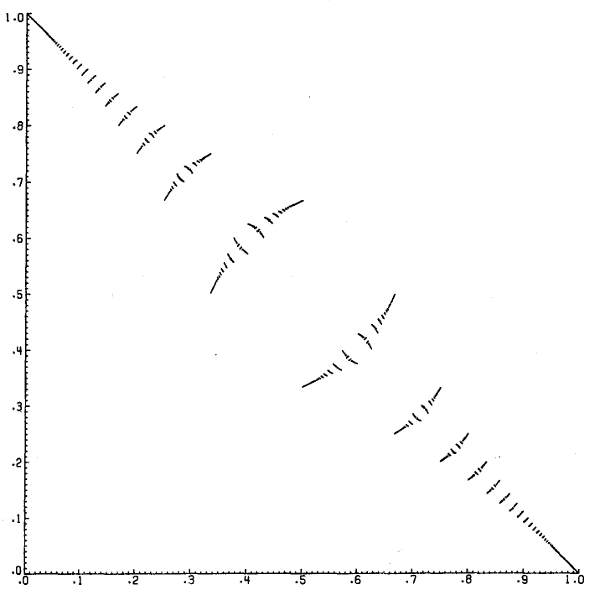
FIGURA 32.Gráfica de la función INT(x). Hay brincos discontinuos en cada valor racional de x.
El hecho de que INT consista nada más que en copias de sí misma puede llevar al lector a pensar que es demasiado efímera para existir. Su definición impresiona como excesivamente circular. ¿Cómo romper el círculo? Es un asunto sobremanera interesante. Lo más importante a tener en cuenta es que, para describir INT a alguien que no lo haya visto, no basta con decirle, “consiste en reproducciones de sí misma”. La otra mitad de la historia —la mitad no recursiva— indica dónde se ubican esas reproducciones dentro del cuadro y cómo han sido deformadas con relación a la gráfica de tamaño natural. Únicamente la combinación de estos dos aspectos podrá especificar la estructura de INT. Es exactamente como en la definición de los números de Fibonacci, donde eran necesarias dos líneas: una para definir la recursividad, la otra para definir la base (esto es, los valores iniciales). Para ser más concreto: si a uno de los valores de base se lo convierte en 3, en lugar de 1, el resultado es una secuencia enteramente distinta, conocida como la secuencia de Lucas:

En la definición de INT, lo que corresponde a la “base” es un diseño (figura 33a) compuesto por muchas casillas que muestran dónde se ubican las reproducciones y cómo se han distorsionado éstas. Lo llamo el “esqueleto” de INT. Para construir INT a partir de su esqueleto, debe procederse como sigue. Primero, para cada casilla, son necesarias dos operaciones: 1) colocar dentro suyo una pequeña reproducción curvada del esqueleto, guiándose por la línea curva situada en su interior; 2) borrar el rectángulo y la línea curva. Una vez hecho esto con todas las casillas del esqueleto original, se tendrán muchos “miniesqueletos” en lugar de uno solo mayor. Debe repetirse ahora el proceso, un nivel más abajo, con todos los “miniesqueletos”. Y luego una vez más, y una vez más… De este modo se obtendrá una aproximación, en el límite, a una gráfica exacta de INT, pese a que no se pueda culminar nunca la tarea. Incluyendo el esqueleto dentro de sí mismo una y otra vez, gradualmente quedará construida una gráfica de INT “desde la nada”. Pero en rigor la “nada” no es tal: es un diseño.
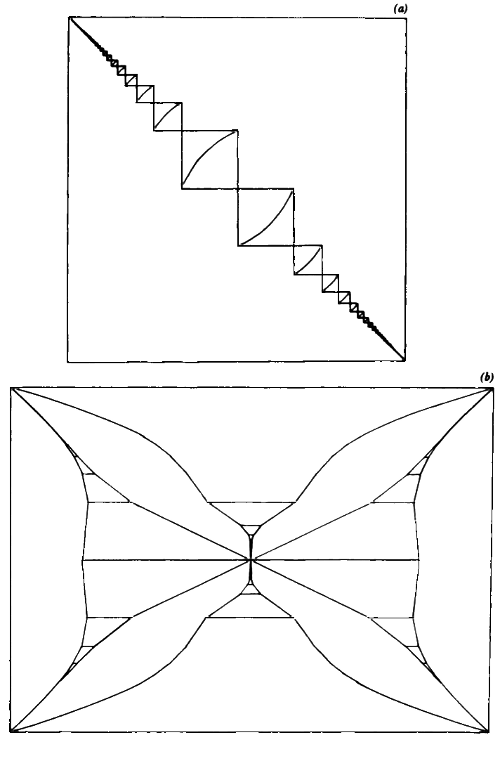
FIGURA 33. (a) El esqueleto a partir del cual se puede construir INT mediante sustituciones recursivas. (b) El esqueleto a partir del cual se puede construir el diseño G mediante sustituciones recursivas.
Para abordar esto de modo todavía más dramático, imaginemos que se conserva la parte recursiva de la definición de INT, pero modificando el diseño inicial, el esqueleto. Una variante de éste es mostrada en la figura 33b, y también presenta casillas que se van haciendo paulatinamente más pequeñas a medida que se acercan a las esquinas. Si se incluye este segundo esqueleto sucesivas veces dentro de sí mismo, se obtendrá la gráfica clave de mi tesis doctoral, a la que llamo diseño G (figura 34). (En realidad, también es necesario cierto grado de complicación distorsiva, pero la idea básica es la de autoinclusión). El diseño G, así, ingresa a la familia INT. Es un pariente lejano, pues su esqueleto es completamente distinto —y notablemente más complejo— que el de INT. No obstante, la parte recursiva de la definición es idéntica, y eso es lo que funda los lazos familiares.
No quiero mantener por más tiempo el suspenso acerca del origen de estas bellas gráficas. INT significa “intercambio”, y proviene de un problema que abarca “secuencias Eta”, las cuales se relacionan con fracciones continuas. La idea fundamental que subyace a INT es que los signos más y menos son intercambiados dentro de cierta clase de fracción continua. Como consecuencia, INT(INT(x)) = x.
INT tiene la propiedad de que, si x es racional, también lo es INT(x); si x es cuadrático, también lo es INT(x). Ignoro si esta tendencia se mantiene en niveles algebraicos más elevados. Otro aspecto atrayente de INT es que, en todos los valores racionales de x presenta brincos discontinuos, mientras que en los valores irracionales de x hay continuidad.
El diseño G surgió de un tratamiento altamente especulativo de la pregunta: “¿Cuáles son las energías permitidas de electrones en un cristal dentro de un campo magnético?”. Este problema resulta curioso porque es un encuentro entre dos situaciones muy simples, y fundamentales, de orden físico: un electrón en un cristal perfecto, y un electrón en un campo magnético homogéneo. Estos dos problemas son bien conocidos, y sus soluciones clásicas parecen casi incompatibles entre sí. Por consiguiente, tiene un gran interés la observación de los pasos que da la naturaleza para reconciliarlas. Cuando ocurren, la situación cristal-sin-campo-magnético y la situación campo-magnético-sin-cristal presentan un aspecto en común: andando el tiempo, el electrón asume un comportamiento periódico. Resulta que, cuando ambas situaciones son combinadas, la razón correspondiente a sus dos períodos pasa a ser el parámetro clave. En realidad, dicha razón retiene toda la información relativa a la distribución de las energías permitidas de electrones, pero solamente revela el secreto si es desarrollada dentro de una fracción continua.

FIGURA 34. Diseño G: una gráfica recursiva que muestra cintas de energía de electrones, en un cristal idealizado, dentro de un campo magnético. α, que representa la fuerza del campo magnético, transita verticalmente entre 0 y 1. La energía transita horizontalmente. Los segmentos de línea horizontales son cintas de energías permitidas de electrones.
El diseño G muestra esa distribución. El eje horizontal representa la energía, y el vertical la razón mencionada, a la que podremos llamar “α”. En la base, a es cero, y en la cima es la unidad. Cuando α es cero, no hay campo magnético. Cada uno de los segmentos de recta que integran el diseño G es una “cinta de energía”, esto es, representa los valores de la energía permitida. Las franjas vacías de diferentes dimensiones que se escalonan a través del diseño G representan, en consecuencia, zonas de exclusión de energía. Uno de los atributos más pasmosos del diseño G consiste en que, cuando α es racional (digamos p/q, para mayor claridad), hay exactamente q de aquellas cintas (pese a que, cuando q es constante, dos de las cintas se “besan” en el centro). Y si α es irracional, las cintas se contraen, convirtiéndose en puntos; de éstos se presenta una cantidad infinita, muy diseminadamente distribuida en un llamado “conjunto de Cantor”: otra entidad de definición recursiva, nacida en el ámbito de la topología.
El lector puede muy bien preguntarse si una estructura tan intrincada fue descubierta con motivo de un experimento. Francamente, yo sería la persona más sorprendida del mundo si el diseño G surgiera en el transcurso de una experimentación. La fisicalidad del diseño G reside en el hecho de que sigue el modo adecuadamente matemático que se aplica al tratamiento de problemas, si bien menos especulativos, de esta clase. En otras palabras, el diseño G es exclusivamente una contribución a la física teórica… y de ningún modo una sugerencia a los experimentadores en cuanto a observaciones previsibles… Un amigo agnóstico quedó tan impresionado con la infinita cantidad de infinitos del diseño G, que llamó a éste “una imagen de Dios”: no creo, en absoluto, que ello constituya una blasfemia.
Recursividad en el nivel inferior de la materia
Hemos visto recursividad en la gramática de los idiomas, hemos visto árboles geométricos recursivos que crecen inacabablemente hacia arriba y hemos visto una forma de ingreso de la recursividad en la teoría física de los estados sólidos. Y ahora vamos a ver una forma bajo la cual el mundo entero aparece hecho de recursividad. Se relaciona con la estructura de las partículas elementales: electrones, protones, neutrones y los diminutos quanta de la radiación electromagnética llamados “fotones”. Veremos que estas partículas están —en un sentido determinado que sólo puede ser rigurosamente definido por la mecánica cuántica relativista— incluidas unas dentro de otras de una manera que puede ser descrita recursivamente, quizá hasta por medio de algún género de “gramática”.
Comenzamos con la observación de que, si las partículas no interactuasen entre sí, las cosas serían increíblemente simples. A los físicos les agradaría un mundo así, pues podrían prever fácilmente el comportamiento de todas las partículas (siempre que existieran tísicos en tal mundo). Las partículas exentas de interacción son llamadas desnudas y se trata de creaciones puramente hipotéticas: no existen.
Ahora bien, cuando “ponemos en marcha” las interacciones, las partículas se entrelazan recíprocamente del mismo modo en que lo hacían las funciones F y M, o en que lo hace la gente que se une en matrimonio. Se dice de las partículas que son “normalizadas”: una palabra sin gracia, pero intrigante. Lo que sucede es que ninguna de estas partículas puede ser ni siquiera definida sin referencia a todas las demás partículas: y la definición de éstas, a su vez, depende de su relación con las anteriores, etc., y así, giro a giro, en un circuito sin final.
Seamos un poco más concretos. Nos limitaremos a sólo dos clases de partículas: electrones y fotones. También tenemos que poner en juego las antipartículas del electrón, los positrones (los fotones tienen su propia antipartícula). Imaginemos un mundo inerte, donde un electrón desnudo desea propagarse desde un punto A a un punto B, igual que Zenón en mi Invención a tres voces. Un físico trazaría este dibujo:
Existe una expresión matemática que corresponde a esta línea y a sus extremos y que es fácil de formular. Mediante ella, un físico puede entender el comportamiento del electrón en su trayectoria.
Ahora, “ponemos en marcha” la interacción electromagnética, por medio de la cual interactúan electrones y fotones. Aunque no haya fotones en la escena, se producirán consecuencias profundas, pese a tratarse de una trayectoria simple. En particular, nuestro electrón adquirirá ahora capacidad de emitir y luego reabsorber fotones virtuales: fotones que nacen y mueren antes de poder ser vistos. Podemos mostrar así tal proceso:
Cuando nuestro electrón se propaga, puede emitir y reabsorber un fotón tras otro, o bien incluirlo, como se muestra a continuación:
Las expresiones matemáticas correspondientes a estos diagramas —llamadas “diagramas de Feynman”— son fáciles de formular, si bien son más difíciles de calcular que para el electrón desnudo. Pero lo que verdaderamente complica el problema es que un fotón (real o virtual) puede, durante un breve intervalo, caer en el interior de un par electrón-positrón. En tal caso, éstos se anulan recíprocamente y, como por arte de magia, el fotón original reaparece. Esta clase de proceso es la que sigue:
El electrón está señalado por la flecha orientada hacia la derecha, y el positrón por la que apunta a la izquierda.
Tal como el lector lo habrá previsto, estos procesos virtuales pueden ser incluidos unos dentro de otros, y hasta la profundidad que se desee. Ello puede originar ciertos diseños muy complicados, similares al que muestra la figura 35. En este diagrama de Feynman, un electrón individual ingresa por la izquierda, en A, realiza algunas llamativas acrobacias y luego emerge —también un electrón individual— por la derecha, en B. Para un observador externo que no haya visto el embrollado intermedio, parecerá que un electrón ha navegado pacíficamente desde el punto A hasta el punto B. En el diagrama, es posible observar cómo pueden ser “embellecidas” a voluntad las líneas del electrón, y cómo pueden serlo también las del fotón. Este diagrama sería endiabladamente difícil de calcular.

FIGURA 35. Un diagrama de Feynman que muestra la propagación de un electrón renormalizado en su trayecto desde A hasta B. En este diagrama, el tiempo avanza hacia la derecha; por ende, en los segmentos donde la flecha indica que el electrón se dirige hacia la izquierda, se está moviendo “hacia atrás en el tiempo”. Dicho más intuitivamente: un antielectrón (positrón) se está desplazando hacia adelante en el tiempo. Los fotones son sus propias antipartículas; por eso, sus líneas no necesitan flechas.
Hay una especie de “gramática” en estos diagramas que permite la concreción de, únicamente, determinados trazados. Por ejemplo, el que sigue es imposible:
Se puede decir de él que no es un diagrama de Feynman “bien formado”. La gramática es un resultado de las leyes básicas de la física, tales como la conservación de energía, la conservación de las cargas eléctricas, etc. Y, lo mismo que las gramáticas de las lenguas naturales, esta gramática tiene una estructura recursiva, consistente en la inclusión profunda de unas estructuras en el interior de las otras. Es posible diseñar un conjunto de redes de transición recursiva que defina la “gramática” de la interacción electromagnética.
Cuando se hace que interactúen electrones y fotones desnudos dentro de estos recorridos arbitrariamente enmarañados, lo que resulta son electrones y fotones renormalizados. Así, para comprender cómo se propaga un electrón real, material, desde A hasta B, el físico debe contar con una suerte de término medio de los infinitos trazados de que son capaces las partículas virtuales. ¡Es lo de Zenón, mas en grado superlativo!
De tal modo, la cuestión central es que una partícula material —una partícula renormalizada— comprende (1) una partícula desnuda, y (2) un inmenso enmarañamiento de partículas virtuales, inextricablemente entrelazadas en el seno de un laberinto recursivo. La existencia de cada partícula real, entonces, involucra la existencia de una cantidad infinita de otras partículas, integrantes de un “enjambre” que van circundando a aquélla a medida que se propaga. Y cada una de las partículas virtuales del enjambre, por supuesto, arrastra su propio enjambre virtual, y así hasta el infinito.
Los físicos atómicos consideran que tal complejidad excede las posibilidades de manipulación: para entender el comportamiento de electrones y fotones, efectúan aproximaciones que omiten todo lo que vaya más allá de diagramas Feynman enteramente simples. Por fortuna, cuanto más complejo es un diagrama, menor es su aporte. No se conoce ningún método que permita resumir los infinitos diagramas posibles, destinados a manifestar el comportamiento de un electrón real, completamente renormalizado. En cambio, mediante la utilización somera del centenar de diagramas más sencillos, relativos a determinados procesos, los físicos han podido predecir, correctamente, ¡un valor de hasta nueve decimales (el llamado factor g del muón)!
No sólo hay renormalización entre electrones y fotones: dondequiera que exista interacción entre cualquier tipo de partículas, los físicos aplican la noción de renormalización para comprender los fenómenos. Así es como protones, neutrones, neutrinos, mesones pi, quarks —todos los ejemplares de la fauna subatómica— cuentan, dentro de la teoría física, con versiones desnudas y renormalizadas. Y todos los ejemplares y fruslerías de que está compuesto el mundo proceden de estos billones de burbujas alojadas dentro de otras burbujas.
Reproducciones y similitud
Volvamos a considerar el Diseño G. Recordará el lector que, en la Introducción, hablamos de diferentes variedades de cánones. Cada género de canon desarrolla determinada manera de encarar un tema original y de copiarlo mediante un isomorfismo, o transformación donde la información es conservada. Algunas veces, esas reproducciones se presentan ordenadas de abajo hacia arriba, o de adelante hacia atrás, o bien reducidas, o ampliadas… En el Diseño G encontramos todos esos tipos de transformación, y algunos más. Las correspondencias entre el Diseño G en su conjunto y las “copias” de sí mismo que incluye en su propio interior abarcan modificaciones de tamaño, sesgamientos, simetrías, y otras variantes. Empero, se mantiene allí una forma de identidad entre diseños, que el ojo puede percibir con un pequeño esfuerzo, en especial después de haber practicado con INT.
Escher adoptó la idea de hacer, de partes de un objeto, réplicas del objeto mismo, y la concretó en una obra: su grabado Pez y escamas (figura 36). Por supuesto, estos peces y escamas resultan similares sólo si son examinados en un plano lo suficientemente abstracto. Además, cualquiera sabe que las escamas de un pez no son en realidad pequeñas reproducciones del pez, y que las células de un pez no son, tampoco, pequeñas reproducciones del mismo; aun así, el ADN de un pez, presente en todas y cada una de las células del pez, es una “copia” muy plegada de todo el pez: luego, hay algo más que una pizca de verdad en el cuadro de Escher.

FIGURA 36. Pez y escamas, de M. C. Escher (xilografía, 1959).
¿Qué es lo que puede ser “similar” en todas las mariposas? La proyección de una mariposa sobre otra no manifiesta una correspondencia célula por célula, sino entre partes funcionales, y esto puede registrarse con la mediación combinada de dimensiones macro y microscópicas. Es el tipo de isomorfismo que vincula entre sí a todas las mariposas del grabado Mariposas (figura 37), de Escher. Lo mismo sucede con las mariposas, más abstractas, del Diseño G, todas vinculadas entre sí por correspondencias matemáticas que proyectan partes funcionales sobre partes funcionales, aunque ignoren por completo la exactitud en materia de proporciones lineales, de ángulos, etc.
Si llevamos esta indagación de la similitud hasta ubicarla en un plano aún más alto de abstracción, podemos muy bien preguntar, “¿qué es lo similar en todas las obras de Escher?”. Sería absolutamente ridículo intentar la proyección de cada una sobre todas las demás. Lo asombroso es que inclusive un fragmento diminuto de una obra de Escher o de una composición de Bach revelan la respuesta. Exactamente como el ADN de un pez está contenido en el interior de cada minúsculo fragmento de ese pez, así la “rúbrica” de un creador está contenida dentro de cada minúsculo fragmento de sus creaciones. No conocemos otro modo de identificar esto que llamándolo “estilo”: una palabra ambigua y elusiva.

FIGURA 37. Mariposas, de M. C. Escher {grabado en madera, 1950).
Seguimos estrellándonos contra la “similitud en la diversidad” y contra la pregunta:
¿Cuándo son similares dos cosas?
Volveremos muchas veces sobre esto en el presente libro. Lo abordaremos desde todas las perspectivas indirectas posibles, y vamos a ver, al final, cómo esta simple pregunta se relaciona profundamente con la naturaleza de la inteligencia.
No es casual que este tema surja dentro del capítulo dedicado a la recursividad, ya que ésta es un fenómeno donde la “similitud en la diversidad” cumple un papel central. La recursividad se basa en que la “misma” cosa aparece en diferentes niveles al mismo tiempo. Pero los hechos ubicados en los diferentes niveles no son exactamente los mismos: antes bien, lo que hallamos son algunos rasgos constantes en medio de muchos aspectos diferenciales. En el Pequeño laberinto armónico, por ejemplo, las narraciones de los distintos niveles no tienen ninguna relación entre sí: su “similitud” reposa exclusivamente en las dos circunstancias siguientes: (1) se trata siempre de historias; (2) en todas ellas aparecen la Tortuga y Aquiles. Fuera de esto, difieren radicalmente una de otra.
Programación y recursividad: modularidad, bucles, procedimientos
Una virtud esencial, en programación computacional, es la de saber percibir cuándo dos procesos son similares en aquel amplio sentido, pues ello conduce a la modularización, o fraccionamiento adecuado de una tarea en subtareas. Por ejemplo, uno puede tener una secuencia de operaciones similares por efectuar; entonces, en lugar de enunciarlas todas, puede formularse un bucle, el cual indicará a la computadora que realice un conjunto fijo de operaciones, y que luego se mueva en bucle hacia atrás y las realice de nuevo, una y otra vez, hasta que sea satisfecha determinada condición. Ahora bien, el cuerpo del bucle —el conjunto fijo de operaciones que deben repetirse— no necesita, en realidad, estar rigurosamente establecido: puede variar de alguna manera previsible.
Un ejemplo lo brinda la muy sencilla prueba que aplicamos para verificar la primidad de un número natural N, donde comenzamos tratando de dividir N por 2, luego por 3, por 4, por 5, etc., hasta N−1. Si N pasa por estas pruebas sin resultar divisible, es primo. Tómese nota de que cada paso del bucle es similar, pero no igual, al resto de los pasos. Adviértase también que el número de pasos varía de acuerdo a N, por lo que un bucle dotado de una extensión fija no podría servir nunca como prueba uniforme de la primidad. Hay dos criterios de interrupción del bucle: (1) si un número divide exactamente a N, la respuesta deja de ser “NO”; (2) si se llega a N−1, y N se mantiene indivisible, la respuesta deja de ser “SI”.
La noción general que anima a los bucles, así, es la siguiente: realizar repetidas veces determinada serie de pasos interrelacionados, e interrumpir el proceso cuando se cumplen ciertas condiciones específicas. Algunas veces, el número máximo de pasos que componen un bucle será conocido de antemano; otras, hay que limitarse a comenzar y a aguardar hasta que se interrumpa. Este segundo tipo de bucle —al que llamo bucle libre— es arriesgado, porque puede que el criterio de interrupción no sobrevenga nunca, dejando a la computadora en una situación conocida como “de bucle infinito”. La distinción entre bucles delimitados y bucles libres es uno de los conceptos más importantes dentro de la ciencia de la computación, y habremos de dedicarle todo un capítulo, el XIII.
Ahora bien, los bucles pueden incluirse uno dentro de otro. Por ejemplo, supongamos que se quiere verificar la primidad de todos los números comprendidos entre 1 y 5000. Podemos formular un segundo bucle que aplique repetidas veces la prueba descrita más arriba, comenzando con N = 1 y terminando con N = 5000. De este modo, nuestro programa tendrá una estructura de “bucle hecho de bucles”. Tales estructuras son clásicas y, en realidad, se las considera una ventajosa modalidad de programación. Esta clase de bucle autoincluido también aparece en las instrucciones para el montaje de productos corrientes y en actividades como el tejido de punto o de ganchillo, donde bucles muy pequeños son repetidos varias veces dentro de bucles mayores, los cuales son realizados, a su vez, reiteradamente… El resultado de un bucle de nivel inferior puede ser sólo un par de puntadas, mientras que el de un bucle de nivel superior puede ser una parte sustancial de una prenda de vestir.
También en música aparecen bucles a menudo, como por ejemplo cuando una escala (un bucle pequeño) es ejecutada varias veces consecutivas, quizá con un desplazamiento de tono en cada oportunidad. Pongamos por caso el quinto Concierto para Piano de Prokofiev, y la Segunda Sinfonía de Rachmaninoff; ambos, en su último movimiento, contienen extensos pasajes en los cuales son ejecutados bucles-escalas rápidos, lentos o intermedios, en forma simultánea por distintos grupos de instrumentos: el efecto que provocan es notable. Las escalas de Prokofiev suben, las de Rachmaninoff bajan; hay para elegir.
Una noción más amplia que la de bucle es la de subrutina, o procedimiento, ya comentada en alguna medida. La idea básica, aquí, es la reunión de diversas operaciones en un solo grupo, considerado así como unidad individual, bajo una determinada denominación: el procedimiento NOMBRE MODIFICADO, por ejemplo. Ya vimos, a propósito de las RTR, que los procedimientos pueden apelar uno al otro, convocándose entre sí por su nombre, con lo cual quedan expresadas, de modo muy conciso, las secuencias de operaciones que deben efectuarse. Ésta es la esencia de la modularidad en programación; existe modularidad, por supuesto, en los sistemas de sonido de alta fidelidad, en el mobiliario, en la célula viva, en la sociedad humana: dondequiera se encuentre una organización jerárquica.
Lo más frecuente es que se tenga necesidad de un procedimiento que actúe en forma variable, de acuerdo a un contexto. Tal procedimiento puede consistir en un sistema de escudriñamiento de todo lo almacenado en la memoria, para determinar sus acciones con arreglo a ello, o bien en una lista de parámetros explícitos que orienten la adopción de determinaciones. A veces se utilizan ambos métodos. En la terminología RTR, establecer la secuencia de acciones por cumplir equivale a elegir qué recorrido se seguirá. Una RTR a la que se haya perfeccionado con parámetros, y condiciones que guíen la elección de recorridos, es llamada Red de Transición Aumentada (RTA). Una tarea donde se haría preferible una RTA a una RTR es la de producción de oraciones con sentido —por oposición a sin sentido—, ya no compuestas por palabras sueltas, y regidas por una gramática representada por un conjunto de distintas RTA. Los parámetros y condiciones harían posible la incorporación de diversas restricciones semánticas, de modo tal que no serían permitidas yuxtaposiciones al azar, del tipo “un refrigerio desagradecido”. Hablaremos más sobre esto en el Capítulo XVIII.
Recursividad en programas de ajedrez
Un ejemplo clásico de procedimiento recursivo dotado de parámetros es el de elección del “mejor” movimiento en ajedrez. El mejor movimiento sería el que deja a nuestro oponente en la situación más desventajosa; en consecuencia, una verificación de lo buena que es una jugada es simplemente como sigue: suponer que se la ha efectuado, y a continuación evaluar la partida desde el punto de vista del contrincante. ¿Y cómo es la evaluación que éste hace? Claro, él también persigue su mejor movimiento; es decir, recuenta mentalmente todas las jugadas posibles y las evalúa desde su propio punto de vista, a la espera de que resulten desventajosas para nosotros. Ahora bien, hago notar que estamos definiendo recursivamente el “mejor movimiento”, gracias a la simple aplicación de la máxima según la cual lo mejor para un lado es lo peor para el otro. El procedimiento recursivo que persigue el mejor movimiento opera mediante la suposición conjetural de una jugada, ¡seguida por la apelación a uno mismo, puesto en el lugar del oponente! Desde aquí uno conjeturará otro movimiento y se pondrá de inmediato en el papel del oponente de su oponente, o sea en el de uno mismo.
Este proceder recursivo puede avanzar varios niveles en profundidad, ¡pero hay que actuar con el respaldo de alguna referencia! ¿Cómo evaluar las posiciones de un tablero sin efectuar anticipaciones? Existen diversos criterios adecuados para satisfacer tal propósito, como por ejemplo el análisis de la cantidad de piezas con que cuenta cada jugador; cuántas y de qué rango están bajo amenaza; en qué situación se encuentra el dominio del centro, etc. Con el apoyo de estos criterios, el generador recursivo de jugadas se puede volver a sacar de vuelta hacia adelante, a fin de aportar la evaluación que corresponda al nivel extremo de cada una de las diferentes movidas. Uno de los parámetros de la autoapelación, así, tendrá que establecer la cantidad de jugadas que se deben anticipar. La parte externa de la apelación al procedimiento, por su parte, aplicará a este parámetro cierto valor ubicado fuera. Entonces, cada vez que el procedimiento apela recursivamente a sí mismo, el parámetro de anticipación disminuye en 1, de modo que, si se reduce a cero, el procedimiento optará por seguir el camino alternativo: la evaluación no recursiva.
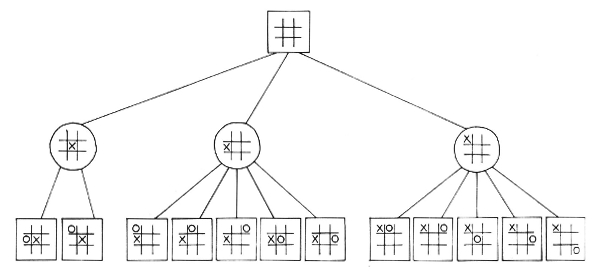
FIGURA 38. La ramificación de un árbol de jugadas y respuestas, correspondiente al comienzo de una partida de gato.
En esta clase de programa destinado a la práctica de un juego, el análisis de cada movimiento genera la elaboración de un llamado “árbol de anticipación”, donde la propia movida es el tronco, las respuestas son las ramas principales, las contrarrespuestas las ramas secundarias, y así sucesivamente. En la figura 38 muestro un árbol de anticipación sencillo, que refleja el comienzo de un juego de gato. Obviar la necesidad de explorar hasta sus más lejanas extremidades un árbol de anticipación es todo un arte. Con relación a los árboles ajedrecísticos, los seres humanos aventajan a las computadoras en este arte; es sabido que los ajedrecistas de mayor nivel, si los comparamos con la mayoría de los programas de juego, anticipan relativamente poco, pero juegan mucho mejor… En las primeras épocas del ajedrez computado, se solía decir que al cabo de diez años aparecería una computadora (o un programa) que iba a convertirse en campeón mundial. Pero cuando transcurrió ese plazo, se tuvo la impresión de que todavía faltaba algo más de diez años para que una computadora ganase el campeonato mundial… lo cual, precisamente, es un fundamento adicional de la un tanto recursiva
Ley de Hofstadter: Siempre toma más tiempo del que se preveía, aun cuando se toma en cuenta la Ley de Hofstadter.
Recursividad e impredictibilidad
Ahora bien, ¿qué vinculación existe entre los procesos recursivos de este capítulo y los conjuntos recursivos de los precedentes? La respuesta involucra la noción de conjunto recursivamente enumerable. Que un conjunto sea r. e. significa que puede ser generado a partir de un grupo de puntos de arranque (axiomas), mediante la aplicación reiterada de reglas de inferencia. Así, el conjunto crece y crece, y sus nuevos elementos se van componiendo, de algún modo, con los elementos anteriores, en una especie de “bola de nieve matemática”. Pero ésta es la esencia de la recursividad: la definición de algo en función de versiones más simples de ello mismo, en lugar de hacerlo explícitamente. Los números de Fibonacci y los números de Lucas, son ejemplos perfectos de conjuntos r. e.: a partir de dos elementos, y gracias a la aplicación de una regla recursiva, echan a rodar una bola de nieve formada por infinitos conjuntos. Es sólo por convención que llamamos r. e. a un conjunto cuyo complemento es, también, “recursivo” y r. e.
La enumeración recursiva es un proceso donde surgen elementos nuevos a partir de elementos anteriores, por la acción de reglas establecidas. Parecen darse muchas sorpresas en estos procesos, como por ejemplo de impredictibilidad de la secuencia Q. Es posible suponer que las secuencias recursivamente definidas de tal tipo poseen la cualidad intrínseca de asumir un comportamiento cada vez más complejo, de suerte que cuanto más se avanza, menor es la predictibilidad.
Esta clase de suposición, si se profundiza un poco en ella, sugiere que los sistemas recursivos, adecuadamente complicados, son lo bastante poderosos como para evadirse de cualquier molde prefijado. ¿Y esto no constituye uno de los atributos que definen la inteligencia? En vez de considerar únicamente programas integrados por procedimientos que apelan recursivamente a sí mismos, ¿por qué no trabajar con procedimientos realmente refinados, mediante la creación de programas que puedan modificarse a sí mismos? Es decir, programas que ejerzan su acción sobre programas, extendiéndolos, mejorándolos, generalizándolos, reordenándolos, etc. Es probable que esta forma de “recursividad entrelazada” sea uno de los elementos sustanciales de la inteligencia.



















