CAPÍTULO IV
Coherencia, completitud y geometría
Significación implícita y explícita
EN EL CAPÍTULO II VIMOS que la significación —al menos dentro del contexto relativamente simple de los sistemas formales— aparece cuando hay un isomorfismo entre símbolos gobernados por reglas, de un lado, y cosas del mundo real, del otro. En general, mientras más complejo es el isomorfismo, más “equipo” —tanto hardware† como software— se requiere para extraer la significación de los símbolos.
Si un isomorfismo es muy simple (o muy familiar), nos inclinamos a decir que el significado a que nos da acceso es explícito: vemos el significado sin ver el isomorfismo. El ejemplo más sobresaliente al respecto es el del lenguaje humano; a menudo la gente atribuye significados a las palabras mismas, sin advertir en absoluto el muy complejo “isomorfismo” que es, en realidad, lo que las dota de significación. Se comete con harta facilidad este error, consistente en atribuir toda la significación al objeto (la palabra), antes que el vínculo entre ese objeto y el mundo real. Se lo puede comparar con la creencia ingenua de que el ruido es un efecto colateral, de carácter necesario, de toda colisión entre dos objetos. Se trata de una creencia falsa, pues dos objetos pueden chocar en el vacío, donde no producirán el menor sonido. En este caso se repite la equivocación que deriva de atribuir el ruido exclusivamente a la colisión, y en no reconocer la función del medio, de lo que hace de vehículo entre los objetos y el oído.
Más arriba entrecomillé la palabra “isomorfismo” para indicar que debe ser tomada con gran cuidado. Los procesos simbólicos que subyacen a la comprensión del lenguaje humano son mucho más complejos que los procesos simbólicos de los sistemas formales convencionales; en consecuencia, si vamos a seguir sosteniendo que los isomorfismos son los vehículos intermediarios de la significación, tendremos que adoptar una concepción mucho más flexible que la utilizada hasta ahora acerca de aquéllos. En mi opinión, en verdad, el elemento clave para responder a la pregunta “¿qué es la conciencia?” tiene que ser el desciframiento de la naturaleza del “isomorfismo” que subyace a la significación.
El significado explícito del Contracrostipunctus
Todo lo anterior nos sirve de prólogo para un examen del Contracrostipunctus, para su estudio en los niveles de la significación. En el Diálogo hay significados explícitos e implícitos; el más visible de los primeros es simplemente la anécdota relatada. Este significado “explícito” es, estrictamente hablando, en gran medida implícito en el sentido de que los procesos cerebrales requeridos para comprender los acontecimientos incluidos en la anécdota, manifestados sólo como signos negros sobre papel blanco, son increíblemente complejos. No obstante, consideraremos dichos acontecimientos como significado explícito del diálogo, y supondremos que todos los lectores aplican más o menos el mismo “isomorfismo” para absorber tal significado a partir de los signos impresos.
De todos modos, me gustaría ser algo más explícito acerca del significado explícito del relato, y comenzaré entonces por referirme a los fonógrafos y a los discos. El aspecto principal es que hay dos niveles de significación en los surcos de los discos. El Nivel Uno es el de la música, pero ¿qué es la música?, ¿una secuencia de vibraciones producidas en el aire, o una sucesión de reacciones emocionales producidas en el cerebro? Es ambas cosas, pero antes de ser respuesta emocional debe ser vibración. Ahora bien, estas últimas son “sacadas” de los surcos por un fonógrafo, es decir, un artefacto relativamente fiel con respecto a lo que se aguarda de él; en realidad, se lo puede remplazar con un alfiler, pero dañando los surcos. Obtenidas las vibraciones, el oído las convierte en excitación de neuronas auditivas dentro del cerebro. Luego, tiene lugar una serie de etapas, a través de las cuales el cerebro transforma gradualmente la secuencia lineal de vibraciones en un modelo complejo de reacciones emocionales interrelacionadas: excesivamente complejo para que lo estudiemos aquí, a pesar de lo mucho que me interesaría hacerlo. Limitémonos pues a pensar en los sonidos transportados por el aire como “Nivel Uno” del significado de los surcos.
¿Cuál es el “Nivel Dos” de significación de los surcos? Es la secuencia de vibraciones producidas en el fonógrafo. Este significado sólo puede surgir después de que el del Nivel Uno ha sido extraído de los surcos, pues son las vibraciones en el aire las que causan las vibraciones en el aparato. Así, el significado del Nivel Dos depende del encadenamiento de dos isomorfismos:
- el isomorfismo existente entre determinada grabación impresa en los surcos, y las vibraciones del aire;
- el isomorfismo existente entre determinadas vibraciones del aire, y vibraciones en el fonógrafo.
El encadenamiento entre ambos isomorfismos es ilustrado por la figura 20. Adviértase que el isomorfismo 1 es el único que da origen al significado Nivel Uno. El significado Nivel Dos es más implícito que el Uno, pues emana de la mediación de dos isomorfismos enlazados. Es el Nivel Dos lo que “estalla por la culata”, generando la destrucción del aparato. El interés principal reside en que la producción del significado Nivel Uno fuerza la producción simultánea del significado Nivel Dos: no hay manera de tener Nivel Uno sin Nivel Dos. De modo que es el significado implícito del disco lo que vuelve a éste, y lo destruye.
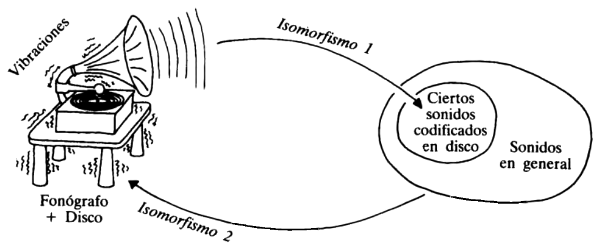
FIGURA 20. Presentación visual del fundamento básico del Teorema de Gödel: dos proyecciones en paralelo, dotadas de un inesperado efecto de búmerang. La primera circula desde los surcos impresos hacia los sonidos, vehiculizados por un fonógrafo. La segunda —cotidiana, pero comúnmente ignorada— va desde los sonidos hacia las vibraciones del fonógrafo. Obsérvese que la segunda proyección existe con independencia de la primera, pues cualquier sonido producido en las cercanías, y no sólo los originados en el fonógrafo, causaría tales vibraciones. La paráfrasis pertinente del Teorema de Gödel dice que hay discos que un fonógrafo no puede hacer escuchar, pues causarían indirectamente su autodestrucción. [Dibujo del autor.]
Corresponde aplicar el mismo razonamiento al grial. Hay una diferencia, consistente en que la analogía entre letras del alfabeto y notas musicales implica otro nivel de isomorfismo, que puede ser llamado “transcripción”, al cual sigue la “traducción”, o sea el acto de convertir las notas musicales en sonidos musicales. Y luego sucede la repercusión de las vibraciones sobre el grial, tal como lo hicieron sobre la serie ascendente de fonógrafos.
Significados implícitos del Contracrostipunctus
¿Y qué pasa con los significados implícitos del Diálogo? (Sí, tiene más de uno). El más simple ya ha sido señalado en los parágrafos anteriores, a saber, que los elementos de las dos mitades del diálogo son rudimentariamente isomórficos entre sí: el fonógrafo se convierte en un violín, la Tortuga pasa a ser Aquiles, el Cangrejo la Tortuga, los surcos impresos el nombre grabado, etc. Una vez advertido este sencillo isomorfismo, se puede ir más allá, y observar que, en la primera mitad, la Tortuga es quien perpetra los desbarajustes, mientras que en la segunda es la víctima; ya lo sabíamos, pero cabe subrayar que su mismo método ha dado un giro y disparado sobre ella. Y recordamos entonces los tiros por la culata de la música impresa en los discos, o de la inscripción grabada en el grial o, inclusive, de la propia colección de búmerangs de la Tortuga. Ciertamente, el tema de esta narración son los disparos por la culata, en dos niveles: los siguientes…
- Nivel Uno:
- Los griales y los discos que lanzan impactos sobre sí mismos.
- Nivel Dos:
- El travieso método de la Tortuga, consistente en aprovechar el significado implícito para causar tiros por la culata… mediante estallidos por la culata.
Por ello, inclusive podemos establecer un isomorfismo entre los dos niveles del relato, correlacionando la forma en que los discos y el grial se transforman en búmerangs de sí mismos, por una parte, con la forma en que el malintencionado método de la Tortuga se transforma después en búmerang que cae sobre ella misma, por la otra. Vista así, la narración misma es un ejemplo de las situaciones contraproducentes que relata. En consecuencia, es válido interpretar que el Contracrostipunctus se refiere indirectamente a sí mismo, en la medida en que su estructura es isomórfica de los sucesos que contiene. (Exactamente del mismo modo en que el grial y los discos se refieren implícitamente a sí mismos mediante los isomorfismos en paralelo de hacer brotar sonidos, y causar vibraciones). Por supuesto, uno puede leer el Diálogo sin percibir esta circunstancia, pero allí está en todo momento.
Correlación entre el Contracrostipunctus y el Teorema de Gödel
Puede que el lector esté sintiendo ya un pequeño vértigo, pero todavía falta lo mejor. (En realidad, algunos niveles de significación implícita no serán mencionados, para que el lector los investigue por su cuenta). La razón fundamental de este Diálogo es ilustrar el Teorema de Gödel, el cual, como ya dije en la Introducción, se apoya vigorosamente sobre dos niveles distintos de significación de las proposiciones propias de la teoría de los números. Cada una de las dos mitades del Contracrostipunctus es una “réplica isomórfica” del Teorema de Gödel. Puesto que tal correlación es la idea central del Diálogo, y teniendo en cuenta que es algo compleja, incluyo más abajo una cuidadosa diagramación:
fonógrafo
⇔
sistema axiomático de la teoría de los números
fonógrafo de baja fidelidad
⇔
sistema axiomático “débil”
fonógrafo de alta fidelidad
⇔
sistema axiomático “fuerte”
fonógrafo “Perfecto”
⇔
sistema completo de la teoría de los números
“diseño” de fonógrafo
⇔
axiomas y reglas del sistema formal
disco
⇔
cadena del sistema formal
disco escuchable
⇔
teorema del sistema axiomático
disco inescuchable
⇔
no teorema del sistema axiomático
sonido
⇔
proposiciones verdaderas de teoría de los números
sonido reproducible
⇔
teorema interpretado del sistema
sonido irreproducible
⇔
proposición verdadera que no es un teorema
título de la canción:
“No puedo ser escuchado mediante el Fonógrafo X”
⇔
significado implícito de la cadena de Gödel:
“No puedo ser derivado dentro del Sistema Formal X”
Lo anterior no abarca en toda su extensión el isomorfismo vigente entre el teorema de Gödel y el Contracrostipunctus, pero sí incluye lo principal. El lector no tiene por qué preocuparse si no capta plenamente el Teorema de Gödel todavía: tenemos varios capítulos por delante antes de abordarlo de lleno. Con todo, la lectura del Diálogo permitirá tomarle un poco el gusto al Teorema, aun sin haberlo estudiado. Ahora, dejo al lector dedicado a la tarea de buscar otros significados implícitos en el Contracrostipunctus. “¡Quaerendo invenietis!”.
El arte de la fuga
Unas pocas palabras acerca de El arte de la fuga: compuesto por Bach durante su último año de vida, se trata de una colección de dieciocho fugas, basadas todas en el mismo tema. Por lo visto, elaborar la Ofrenda Musical sirvió a Bach de inspiración, pues lo decidió a componer un conjunto de fugas sobre un tema mucho más simple, a fin de mostrar la gama completa de las posibilidades inherentes a esa forma. En El arte de la fuga desarrolla aquel tema a través de los modos más complejos que le fue posible. Toda la obra se ajusta a una clave única. La mayoría de las fugas están compuestas para cuatro voces, y van aumentando gradualmente la complejidad y profundidad de su expresión: hacia el final, se encumbran a tales alturas de inextricabilidad que uno sospecha que Bach no podrá ya mantenerse allí… pero lo consigue… hasta el Contrapunctus final, inclusive.
Las circunstancias que provocaron la interrupción de El arte de la fuga (y, al mismo tiempo, de la vida de Bach) fueron las siguientes: como había tenido muy afectada su vista durante años, Bach deseaba ser operado. Así se hizo, pero el resultado fue muy poco satisfactorio, de manera que casi toda la última parte de su existencia la pasó en la ceguera. Pero esto no consiguió apartarlo de su monumental proyecto. Su propósito era formular una exposición completa de la creación fugal, una de cuyas facetas más importantes era el desarrollo de múltiples temas. Proyectó una composición para que siguiese a la última fuga, y con ese objeto inscribió su propio nombre, codificado bajo la forma de notas, como tercer tema. Pero a partir de este verdadero testamento, su salud llegó a hacerse tan precaria que debió abandonar su entrañable proyecto. En su enfermedad, se las arregló para dictar a su yerno un último preludio coral, del que su biógrafo Forkel dijo: “Su forma de piadosa resignación, y de devoción, siempre me ha afectado, cada vez que he asistido a su ejecución, así que puedo decir con toda sinceridad que hubiera preferido no conocer ni este Coral ni el final de la última fuga”.
Problemas provocados por las conclusiones de Gödel
Dice la Tortuga que ningún fonógrafo, por poderoso que sea, puede ser perfecto, en el sentido de estar facultado para reproducir cualquier sonido posible grabado en un disco. Gödel dice que ningún sistema formal, por bien construido que esté, puede ser perfecto, en el sentido de reproducir toda proposición verdadera bajo la forma de teorema. Ahora bien, estos hechos impresionan como fallas sólo cuando se albergan esperanzas nada realistas acerca de las posibilidades de los sistemas formales. A pesar de ello, los matemáticos iniciaron el presente siglo llenos de expectativas ilusorias de esta clase, esperanzados en que el razonamiento axiomático trajese la cura de todos los males. Comenzaron a pensar de otra manera en 1931. El hecho de que la verdad trascienda a la teoremidad, en cualquier sistema formal dado, es conocido como “incompletitud” de tal sistema.
Uno de los aspectos más enigmáticos con relación al método de prueba de Gödel es que emplea esquemas de razonamiento a los cuales, aparentemente, no es posible “encapsular”: resisten su incorporación a cualquier sistema formal. Así pues, a primera vista, se diría que Gödel ha revelado una distancia hasta ahora desconocida, pero profundamente significativa, entre razonamiento humano y razonamiento mecánico. Esta misteriosa diferencia en las posibilidades de los sistemas animados por oposición a los inanimados es reflejada por la diferencia existente entre la noción de verdad y la noción de teoremidad… o bien, en último caso, se trata de una visión romántica de la situación.
El sistema mg modificado y la incoherencia
Para ver la situación de modo más realista, es necesario examinar con mayor profundidad por qué y cómo la significación, en los sistemas formales, es producida por la mediación de isomorfismos. Según creo, esto conduce a una perspectiva aún más romántica del problema. Procederemos pues, a investigar algunas facetas adicionales de la relación entre significación y forma. Nuestro primer paso será construir un nuevo sistema formal, a través de la modificación, muy leve, de nuestro viejo amigo, el sistema mg. Le agregaremos un esquema de axioma (el anterior, y la única regla de inferencia, son conservados):
ESQUEMA DE AXIOMA II: Si x es una cadena de guiones, entonces xm-gx es un axioma.
Luego, evidentemente --m-g-- es un teorema del nuevo sistema, y también lo es --m--g---. Sin embargo, sus respectivas interpretaciones son: “2 más 1 igual a 2”, “2 más 2 igual a 3”. Nos damos cuenta de que nuestro nuevo sistema habrá de contener un gran número de proposiciones falsas (si tomamos las cadenas como proposiciones). Por ende, nuestro nuevo sistema es incoherente con respecto al mundo externo.
Por si esto fuera poco, nuestro nuevo sistema presenta también algunas dificultades internas, puesto que contiene proposiciones incongruentes entre sí, tales como -m-g-- (un axioma anterior) con respecto a -m-g- (un axioma nuevo). En consecuencia, nuestro sistema es incoherente en un segundo sentido: internamente.
¿La única cosa razonable por hacer, pues, sería la completa desestimación del nuevo sistema? Difícilmente. He presentado estas “incoherencias”, de manera deliberada, a través de un método capcioso; en efecto, traté de exponer argumentos ambiguos con la mayor certidumbre posible a fin de inducir a error. Ciertamente, el lector puede haber ubicado las falacias incluidas en mis afirmaciones. La falacia central radica en que, sin el menor cuestionamiento, adopto exactamente las mismas palabras interpretativas para el nuevo sistema que para el anterior. Recordemos que en el último capítulo mencionamos el único motivo que guía la adopción de tales palabras, es decir, el hecho de que los símbolos representan isomórficamente los conceptos con los que están correlacionados mediante la interpretación. Pero si se modifican las reglas que gobiernan el sistema, forzosamente es alterado el isomorfismo; esto es irremediable. Así que las dificultades que deplorábamos en los parágrafos precedentes no son más que falsos problemas, posibles de ser eliminados en un instante, a través de la reinterpretación adecuada de algunos de los símbolos del sistema. He dicho “algunos”, porque no es necesario que todos los símbolos deban ser correlacionados con nuevas nociones. Unos pueden muy bien conservar su “significado”, en tanto que otros lo modificarán.
Reconquistando coherencia
Supóngase, por ejemplo, que reinterpretamos únicamente el símbolo g, dejando constantes los demás; específicamente, daremos a g la siguiente interpretación: “es mayor que o igual a”. Nuestros “contradictorios” teoremas -m-g- y -m-g--, ahora, vuelven a la normalidad ya que su interpretación ajustada se lee: “1 más 1 es mayor que o igual a 1”, y “1 más 1 es mayor que o igual a 2”, respectivamente. A un mismo tiempo hemos evitado, 1) la incoherencia con respecto al mundo exterior, y 2) la incoherencia interna. Y nuestra nueva interpretación es una interpretación significativa; por supuesto, la inicial es no significativa: no significativa para el nuevo sistema; para el sistema mg original, sirve de maravilla. Pero aplicarla al nuevo mg sería tan desacertado y caprichoso como aquella interpretación “caballo-manzana-feliz”, aplicada al sistema mg inicial.
La historia de la geometría euclidiana
A pesar de que he intentado sorprender con la guardia baja al lector, y desconcertarlo un poco, esta lección acerca de cómo interpretar los símbolos mediante las palabras no puede considerarse tremendamente ardua, una vez que se la ha captado. Realmente, no lo es. ¡Y sin embargo se trata de una de las más profundas enseñanzas de toda la matemática del siglo diecinueve! Todo comenzó con Euclides, quien compiló y sistematizó, aproximadamente trescientos años antes de Cristo, todo el saber de su tiempo en materia de geometría plana y del espacio. La obra que resultó, los Elementos, contó con tal solidez que durante más de dos mil años sirvió prácticamente de biblia de la geometría. ¿Cómo se explica una vigencia tan asombrosamente duradera?
La causa principal consiste en que Euclides fue el fundador del rigor en matemática. Los Elementos empiezan por conceptos muy simples, definiciones, etc., y paulatinamente erigen un vasto cuerpo de conclusiones, organizado de forma tal que una conclusión determinada depende exclusivamente de las anteriores. La obra, sin duda, se ajustó a un plan definido, a una arquitectura que le dio fuerza y vigor.
Esa arquitectura, empero, es de un tipo diferente a la de, digamos, un rascacielos (véase figura 21). En este último, el solo hecho de que se mantenga en pie es prueba suficiente de que sus componentes estructurales son capaces de sostenerlo. En un libro de geometría, en cambio, donde se exige que cada proposición se siga lógicamente de las anteriores, no se producirá una fractura visible si una de las pruebas carece de validez; las vigas y columnas no son materiales concretos, sino abstractos. En realidad, la materia de que están hechas las pruebas, en los Elementos de Euclides, es el lenguaje humano: ese elusivo y resbaladizo medio de comunicación, tan lleno de tramas invisibles. ¿Qué ocurre entonces con la fortaleza arquitectónica de los Elementos? ¿Están sostenidos por sólidos componentes estructurales, o habrá en su interior una debilidad estructural?
Cada palabra que empleamos tiene un significado para nosotros, el cual nos guía en nuestra utilización de aquélla. Cuanto más corriente es la palabra, mayores son las asociaciones de que la rodeamos y más profundas son las raíces de su significación. Por ello, cuando alguien define una palabra corriente con la esperanza de mantenerse en los límites de su definición, se puede asegurar de antemano que no lo conseguirá sino que su manejo de esa palabra estará orientado, a causa sobre todo de influencias inconscientes, por las asociaciones almacenadas en la mente. Menciono esto porque es precisamente el tipo de problema provocado por Euclides en sus Elementos, al pretender la definición de palabras comunes y corrientes tales como “punto”, “línea recta”, “círculo” y otras similares. ¿Cómo puede definirse algo de lo cual ya todo el mundo tiene un concepto claro? El único recurso consiste en precisar que la palabra definida debe ser considerada un término técnico, y alejada de toda confusión con la palabra de uso cotidiano que se deletrea igual. El caso es que Euclides no hizo esta salvedad, porque creyó que los puntos y las líneas de los Elementos eran, sin duda alguna, los puntos y las líneas del mundo real. En la medida en que no se ocupó de disipar aquel género de asociaciones, Euclides alentó a sus lectores a ejercer libremente sus facultades asociativas…

FIGURA 21. Torre de Babel, de M. C. Escher (xilografía, 1928).
Esto puede dar la impresión de un panorama más bien caótico, y es un poco injusto hacia Euclides, quien estableció axiomas, o postulados, previstos para servir de pruebas de las proposiciones. Pero sólo previó estas pruebas, lo cual se constituyó en un nuevo error pues, como consecuencia inevitable del empleo de vocablos corrientes, algunas de las representaciones suscitadas por éstos se deslizaban dentro de dichas verificaciones. Ahora bien, quien vaya a analizar en los Elementos tales mecanismos no va a encontrar, en absoluto, vacíos evidentes en los pasos que sigue el razonamiento. Por el contrario, aquéllos son muy agudos, pues Euclides fue un pensador penetrante que no habría cometido errores ingenuos. Sin embargo, hay fisuras en casi toda obra clásica, generadoras de ligeras imperfecciones; no es para lamentarlo, sino para avanzar en cuanto a la capacidad de apreciación de la diferencia que existe entre el rigor absoluto y el relativo. A largo plazo, la falta de rigor absoluto de Euclides ha sido la causa de algunas de las más fértiles revoluciones producidas dentro de la matemática, dos mil años después de haber escrito su obra.
Euclides aportó cinco postulados para que sirviesen como “planta baja” del infinito rascacielos de la geometría, donde los Elementos constituyen sólo el primero, entre centenares de pisos. Los primeros cuatro postulados son bastante concisos y transparentes:
- Entre dos puntos cualesquiera puede ser trazado un segmento de recta.
- Cualquier segmento de recta puede ser extendido indefinidamente en una línea recta.
- Dado cualquier segmento de recta, puede ser trazado un círculo que tenga al segmento como radio y a uno de los extremos como centro.
-
Todos los ángulos rectos son congruentes.
Pero el quinto ya no es tan elegante:
- Si son trazadas dos líneas de modo que intersecten con una tercera de manera tal que la suma de los ángulos internos, sobre uno de los lados, sea menor que dos ángulos rectos, esas dos líneas deben inevitablemente intersectarse entre sí sobre el otro lado, si son extendidas lo suficiente.
Pese a que nunca lo reconoció explícitamente, Euclides consideraba este postulado algo inferior al resto, pues se las arregló para no tener que aplicarlo en las demostraciones correspondientes a sus primeras veintiocho proposiciones. Así, éstas pertenecen a lo que se puede llamar la “geometría de los cuatro postulados”, es decir, la parte de la geometría que puede ser derivada a partir de los cuatro primeros postulados de los Elementos, sin intervención del quinto postulado. (También se la suele llamar geometría absoluta). Sin duda, Euclides habría preferido, de muy buena gana, demostrar este patito feo, en lugar de tener que darlo por supuesto. Mas no descubrió la demostración, y entonces debió suponerlo.
Pero los seguidores de Euclides no se contentaron con tener que dar por supuesto el quinto postulado. Durante siglos, incontables personas entregaron incontables años de sus existencias al propósito de probar que ese postulado era parte integrante de la geometría de los cuatro postulados. En 1763, fueron publicadas por lo menos veintiocho demostraciones distintas, ¡todas erróneas! (Alguien llamado G. S. Klügel dedicó una disertación a criticarlas). Todas esas demostraciones insuficientes incurren en la equivocación de confundir las intuiciones cotidianas con los atributos estrictamente formales. Obvio es decir que el grueso de estas “demostraciones” no conserva en la actualidad ningún interés matemático o histórico… pero hay ciertas excepciones.
Las muy diferentes caras de Nouclides
Girolamo Saccheri (1667-1733) fue contemporáneo de Bach. Tenía la ambición de liberar a Euclides de toda imperfección. Después de elaborar algunos trabajos sobre problemas lógicos, resolvió intentar la aplicación de una nueva perspectiva a la demostración del célebre quinto postulado.
Vamos a imaginar que suponemos su opuesto, y que en adelante utilizamos eso como quinto postulado… Seguramente, al poco tiempo se nos creará una contradicción. Puesto que ningún sistema matemático puede tolerar una contradicción, quedará demostrada la falsedad de nuestro quinto postulado, y en consecuencia la validez del original, acuñado por Euclides. No hace falta ampliar esta analogía: baste decir que, muy hábilmente, Saccheri desarrolló proposición tras proposición de “geometría saccheriana” hasta que se aburrió; en ese punto, decidió que había obtenido una proposición “repugnante a la naturaleza de la línea recta”, lo cual era exactamente su propósito: la contradicción afanosamente perseguida. Publicó entonces su trabajo bajo el título Euclides liberado de toda imperfección, y luego murió.
Lamentablemente, al actuar así se despojó a sí mismo de notables glorias póstumas, puesto que de modo inadvertido había descubierto lo que más tarde sería conocido como “geometría hiperbólica”. Cincuenta años más tarde, J. H. Lambert volvió a “errar por poco”, aproximándose aún más al centro, si cabe. Finalmente, cuarenta años después de Lambert, y noventa después de Saccheri, la geometría no euclidiana fue intrínsecamente reconocida, es decir, en su carácter de auténtica nueva cualidad de la geometría: una bifurcación en la hasta entonces unitaria corriente de la matemática. En 1823 se produjo el descubrimiento de la geometría no euclidiana, por obra simultánea —en una de esas coincidencias extraordinarias— de dos matemáticos, el húngaro János (o Johann) Bolyai, de veintiún años, y el ruso Nikolai Lobachevski, de treinta. El mismo año, irónicamente, el gran matemático francés Adrien-Marie Legendre obtuvo lo que él llamó una demostración del quinto postulado de Euclides, trabajando muy apegado a las líneas fijadas por Saccheri.
EL padre de János, Farkas Bolyai, fue gran amigo del célebre Gauss, y dedicó por su parte muchos esfuerzos a tratar de probar el quinto postulado. En carta a su hijo, intentaba disuadirlo de meditar en estos problemas:
No te sumerjas en el estudio de las paralelas. Conozco ese camino hasta el final. He atravesado esa noche sin fondo, que consumió toda la luz y todo el goce de mi existencia. Te lo ruego, deja en paz la ciencia de las paralelas… Yo me dispuse a sacrificarme en beneficio de la verdad; estaba decidido a convertirme en un mártir que desalojaría el error del seno de la geometría, y se la devolvería purificada a la humanidad. He realizado una monstruosa, enorme labor; mis logros han sido mucho más plenos que los de otros, pero no he podido cumplir por entero la tarea. Aquí es verdad aquello de que si paullum a summo discessit, vergit ad imum. He emprendido el regreso al ver que ningún hombre puede llegar al fondo de esta oscuridad. He emprendido el regreso desconsolado, compadeciéndome y compadeciendo a la humanidad… He atravesado todos los escollos de este infernal Mar Muerto, y he vuelto siempre con el mástil roto y las velas rasgadas. La decadencia de mi voluntad, y mi ruina, tienen esta causa. Irreflexiblemente, expuse mi vida y mi felicidad: aut Caesar aut nihil.[1]
Pero más tarde, cuando estuvo convencido de que su hijo, realmente, “tenía algo”, le urgió a hacerlo conocer, previendo lúcidamente la simultaneidad que es tan frecuente en los descubrimientos científicos:
Cuando llega el tiempo de sazón para ciertas cosas, éstas aparecen en diferentes lugares, a la manera de las violetas que se abren en los comienzos de la primavera.[2]
¡Cuán verdadero resultó esto último en el caso de la geometría no euclidiana! En Alemania, el mismo Gauss y algunos otros matemáticos, trabajando en forma relativamente independiente, formularon ideas no euclidianas. Un abogado llamado F. K. Schweikart, por ejemplo, quien escribió en 1818 a Gauss, describiendo una nueva geometría “astral”; y también su sobrino, F. A. Taurinus, que elaboró desarrollos trigonométricos no euclidianos; o F. L. Wachter, alumno de Gauss que falleció en 1817, a los veinticinco años, tras llegar a varias conclusiones profundas en materia de geometría no euclidiana.
La orientación que siguió la geometría no euclidiana consistió en “considerar textualmente” las proposiciones surgidas de geometrías como las de Saccheri y Lambert. Las proposiciones de Saccheri son “repugnantes a la naturaleza de la línea recta” solamente en la medida en que uno se mantenga obediente de las nociones preconcebidas en cuanto a la “línea recta”. Si, en cambio, uno puede despojarse de tales nociones y, sencillamente, dejar que la “línea recta” sea algo que satisface las nuevas proposiciones, se conseguirá contar con un punto de vista radicalmente nuevo.
Términos indefinidos
Esto ya debería sonar familiar, especialmente porque retornaremos al sistema mg, y a su variante, en la cual los símbolos adquirieron significados pasivos en virtud de la función que debían cumplir en los teoremas. El símbolo g es particularmente interesante, puesto que su “significado” cambió cuando fue agregado un nuevo esquema de axioma. De manera exactamente igual, uno puede dejar que el significado de “punto”, “línea”, etc., sea determinado por el conjunto de teoremas (o proposiciones) dentro de los cuales aparezcan. Éste fue el gran avance de los descubridores de la geometría no euclidiana. Descubrieron diferentes géneros de geometrías no euclidianas mediante la negación del quinto postulado de Euclides, practicada de diversas maneras y llevada hasta sus últimas consecuencias. Para hablar en términos estrictos, ellos (incluido Saccheri) no negaron directamente el quinto postulado, sino que optaron por negar un postulado equivalente, llamado el postulado de las paralelas, el cual dice así:
Dada cualquier línea recta, y un punto fuera de ella, existe una y sólo una línea recta que pase a través de ese punto sin intersectar nunca con aquella línea, por mucho que se la prolongue.
Se dice entonces que la segunda línea es paralela a la primera. Si uno afirma que tal línea no existe, ingresa en la geometría elíptica; si uno afirma que existen por lo menos dos líneas semejantes, se ingresa en la geometría hiperbólica. Además, la razón para que tales variantes sean llamadas “geometrías” es que su componente central sigue siendo la geometría absoluta, o de los cuatro postulados. La presencia de este elemento es lo que crea la posibilidad de pensar que aquéllas describen las propiedades de alguna clase de espacio geométrico, aun cuando tal espacio no sea tan intuible como el espacio corriente.
En verdad, la geometría elíptica puede ser concebida sin dificultad. Todos los “puntos”, “líneas” y demás tienen que ser parte de la superficie de una esfera común. Vamos a escribir “PUNTO” cuando se quiera significar el término técnico, y “punto” cuando se trate del sentido cotidiano. Luego, podemos decir que un PUNTO consiste en un par de puntos opuestos diametralmente sobre la superficie de la esfera. Una LINEA es un gran círculo sobre la esfera (un círculo que, igual que el ecuador, tiene su centro en el centro de la esfera). Bajo estas interpretaciones, las proposiciones de la geometría elíptica se refieren a hechos que suceden sobre una esfera, no sobre un plano, aunque incluyan palabras como “PUNTO” y “LINEA”. Adviértase que dos lineas siempre intersectarán exactamente en un único PUNTO. Y del mismo modo que dos LINEAS determinan un punto, así dos PUNTOS determinan una LINEA.
Manejando palabras tales como “PUNTO” y “LINEA” como si tuvieran solamente el significado que les asignan las proposiciones donde aparecen, damos un paso adelante hacia la plena formalización de la geometría. Esta versión semiformal todavía emplea una gran cantidad de palabras tomadas en su significado usual (por ejemplo: “el”, “la”, “si”, “y”, “determinar”, “tener”), a pesar de que la significación cotidiana ha sido desalojada de palabras específicas como “PUNTO” y “LINEA”, las que son denominadas, a continuación, términos indefinidos. Términos indefinidos, igual que m y g dentro del sistema mg, que se transforman en definidos a través de la acción implícita de todas las proposiciones en que aparecen, antes que a través de la acción explícita de una definición.
Se podría sostener que una definición integral de los términos indefinidos depende solamente de los postulados, ya que las proposiciones que se siguen de los postulados están implicadas en ellos. Este criterio diría que los postulados son definiciones implícitas de los términos indefinidos, todos los cuales, a la vez, son definidos por la relación que los vincula entre sí.
La posibilidad de interpretaciones múltiples
Una formalización completa de la geometría tendría que dar el drástico paso de convertir a todo término en indefinido; es decir, de transformar a todo término en un símbolo “no significativo” de un sistema formal. Pongo entre comillas “no significativo” porque, como sabemos, los símbolos recogen automáticamente un significado pasivo en el interior de los teoremas donde aparecen. Pero el problema de si se advierte ese significado es de otra índole, pues para hacerlo se requiere haber hallado un conjunto de conceptos que puedan ser vinculados, mediante un isomorfismo, con los símbolos del sistema formal. Si se emprende la formalización de la geometría, es presumible que se tenga prevista una interpretación para cada símbolo, a fin de crear los significados pasivos en el interior del sistema. Así hice con m y con g al construir el primer sistema mg.
Pero puede haber allí otros significados pasivos, potencialmente perceptibles, que nadie había advertido. Por ejemplo, en el sistema mg original apareció por sorpresa la interpretación de m como “igual a” y de g como “restado de”. Aun cuando se trate de una muestra más bien trivial, contiene la esencia de la noción de que los símbolos pueden tener muchas interpretaciones significativas: corresponde al observador la tarea de buscarlas.
Podemos sintetizar nuestras observaciones anteriores a la luz de la palabra “coherencia”. Comenzamos nuestra exposición elaborando lo que parecía ser un sistema formal incoherente: carecía de coherencia interna tanto como externa con el mundo real. Pero un momento después nos rectificamos, al comprender nuestro error, consistente en adoptar interpretaciones inadecuadas para los símbolos. Modificando entonces las interpretaciones, recuperamos coherencia. Queda ahora claro que la coherencia no es un atributo de un sistema formal per se, sino que depende de las interpretaciones que se asignen a éste. Por lo mismo, tampoco la incoherencia es un atributo intrínseco de ningún sistema formal.
Distintas variedades de coherencia
Hemos estado hablando extensamente de “coherencia” e “incoherencia” sin definirlas, apoyándonos precisamente en las nociones tradicionales de uso diario. Pero ahora vamos a expresar con exactitud qué significa coherencia (de un sistema formal, vinculada a una interpretación): significa que todo teorema, al ser interpretado, deviene una proposición verdadera. Y diremos que la incoherencia tiene lugar cuando aparece por lo menos una proposición falsa entre los teoremas interpretados.
Estas precisiones parecen referirse a la incoherencia con respecto al mundo externo, ¿y qué diremos acerca de las incoherencias internas? Se presume que un sistema será internamente incoherente si contiene dos o más teoremas cuyas interpretaciones son incompatibles entre sí. Veamos, por ejemplo, un sistema formal que tenga únicamente los tres siguientes teoremas: TmZ, ZmE y EmT. Si la interpretación de T es “la Tortuga”; la de Z, “Zenón”; la de E, “Egbert”; y la de xmy, “x siempre da mate a y en ajedrez”, tendremos entonces estos teoremas interpretados:
- La Tortuga siempre da mate a Zenón en ajedrez.
- Zenón siempre da mate a Egbert en ajedrez.
- Egbert siempre da mate a la Tortuga en ajedrez.
No son proposiciones incompatibles, aunque describan un círculo de ajedrecistas más bien extraño. De ahí que, bajo esta interpretación, el sistema formal del cual estas tres cadenas son teoremas tiene coherencia interna; así es, a pesar de que, desde el punto de vista de la realidad de los hechos, ninguna de las tres proposiciones es verdadera. La coherencia interna no requiere que todos los teoremas resulten verdaderos, sino solamente compatibles entre sí.
Supongamos ahora que xmy debe ser interpretado “x fue inventado por y”. Tendríamos:
- La Tortuga fue inventada por Zenón.
- Zenón fue inventado por Egbert.
- Egbert fue inventado por la Tortuga.
En este caso, no importa si las proposiciones singulares son verdaderas o falsas, y quizá no haya forma de determinar su verdad o falsedad. Pero sí es seguro que las tres no pueden ser verdaderas al mismo tiempo. De tal modo, la interpretación hace que el sistema se vuelva internamente incoherente. Esta incoherencia interna no depende de la interpretación de las tres letras mayúsculas, sino solamente de la m, y del hecho de que las tres mayúsculas son cíclicamente permutadas en torno a las apariciones de m. Así, es posible advertir la incoherencia interna aun sin haber interpretado todos los símbolos del sistema formal (en este caso, basta con interpretar un solo símbolo). Cuando ya han sido asignadas interpretaciones a un número suficientemente amplio de símbolos, puede hacerse claro que no hay forma de interpretar al resto de modo que todos los teoremas resulten verdaderos. Pero no se trata de una cuestión de verdad, sino de posibilidad. Los tres teoremas resultarían falsos si las mayúsculas fuesen interpretadas como nombres de personas reales, pero no por eso llamaríamos internamente incoherente al sistema: para poder hacerlo, nos debemos fundar en la circularidad, combinada con la interpretación de la letra m. (A propósito del tema, el lector encontrará más comentarios sobre este “triángulo creativo” en el Capítulo XX).
Mundos hipotéticos y coherencia
Hemos enunciado dos maneras de analizar la coherencia: según la primera, un sistema-más-interpretación es coherente con el mundo externo si todo teorema resulta verdadero al ser interpretado; según la segunda, un sistema-más-interpretación es internamente coherente si todos los teoremas resultan recíprocamente compatibles al ser interpretados. Ahora bien, existe una relación estrecha entre ambos tipos de coherencia. Para determinar si varias proposiciones son compatibles entre sí, se podría imaginar un mundo donde todas ellas sean verdaderas al mismo tiempo. Luego, la coherencia interna dependería de la coherencia con respecto al mundo externo… sólo que ahora el “mundo externo” es cualquier mundo imaginario, y no el que corresponde a nuestra existencia diaria. Pero ésta es una conclusión demasiado vaga e insatisfactoria. ¿En qué consiste un mundo “imaginario”? Después de todo, ¿es posible imaginar un mundo donde tres personajes se inventan cíclicamente entre sí? ¿Es posible imaginar un mundo donde haya círculos cuadrados? ¿Es un mundo imaginario el sostenido por las leyes de Newton y no por la relatividad? ¿Es posible imaginar un mundo donde existan cosas que sean simultáneamente verdes y no verdes? ¿O un mundo con animales que no estén hechos de células? ¿O donde Bach improvise una fuga a ocho voces sobre un tema del Rey Federico el Grande? ¿O donde haya insectos más inteligentes que el hombre? ¿O donde las tortugas jueguen al fútbol… o hablen? Una tortuga hablando de fútbol sería una anomalía, por supuesto.
Algunos de estos mundos parecen más imaginarios que otros, ya que incluyen contradicciones lógicas —como la de verde y no verde—, mientras que otros parecen, en función de los deseos de un mundo mejor, “plausibles”: Bach improvisando una fuga a ocho voces, o animales que no estén hechos de células, por ejemplo. O, inclusive, llegar a pensar en un mundo regido por leyes físicas diferentes… Genéricamente, entonces, sería posible establecer diferentes grados de coherencia. Por ejemplo, el menos exigente sería el de “coherencia lógica”, el cual no establecería restricciones de ninguna índole, salvo las de la lógica. Más específicamente, un sistema-más-interpretación sería lógicamente coherente en tanto ningún par de sus teoremas, al ser interpretados como proposiciones, encierre una contradicción; y matemáticamente coherente en tanto los teoremas interpretados no violen la matemática; y físicamente coherentes en tanto los teoremas interpretados sean compatibles con las leyes de la física; luego seguiría la coherencia biológica, y así por el estilo. Dentro de un sistema biológicamente coherente, podría haber un teorema cuya interpretación fuese la proposición “Shakespeare escribió una ópera”, pero no un teorema cuya interpretación fuese la proposición “Existen animales carentes de células”. Hablando en términos amplios, estas clases más imaginativas de incoherencia no están estudiadas, a causa de que son muy difíciles de desenmarañar. ¿Qué clase de incoherencia, por ejemplo, es la que atañe al problema de los tres personajes que se inventan entre sí cíclicamente? ¿Lógica? ¿Física? ¿Biológica? ¿Literaria?
Por lo común, la frontera entre lo que no interesa y lo que sí interesa es trazada entre la coherencia física y la coherencia matemática. (Por supuesto, son los matemáticos y los lógicos quienes se encargan del trazado: difícilmente alguien imparcial). Esto significa que las clases de incoherencia que “cuentan”, dentro de los sistemas formales, son únicamente la lógica y la matemática. Ajustándonos a esta convención, todavía no hemos podido encontrar una interpretación que torne incoherente el trío de teoremas TmZ, ZmE, EmT. Lo podremos conseguir si interpretamos m como “es mayor que”. ¿Qué se hace con T, Z y E? Pueden ser interpretados como números naturales: por ejemplo, Z como 10, T como 13 y E como 15. Obsérvese que de esta forma dos teoremas resultan verdaderos, y uno falso. Si, en cambio, interpretamos Z como 14, tendríamos dos falsedades y una verdad. Pero en cualquiera de los casos, ha surgido la incoherencia. En realidad, los valores asignados a T, Z y E no vienen al caso, en la medida en que se da por entendido que están dentro del marco de los números naturales. Otra vez, entonces, vemos un caso donde sólo es necesario interpretar algo, para reconocer la incoherencia interna.
Introducción de un sistema formal en otro
El ejemplo anterior, donde algunos símbolos contaban con interpretaciones mientras que otros no, nos recuerda la construcción de la geometría mediante el lenguaje natural, que apela al empleo de determinadas palabras en función de términos indefinidos. En este caso, las palabras son divididas en dos clases: las que conservan un significado fijo e inmutable, y aquellas cuyo significado debe ser reajustado hasta que el sistema adquiera coherencia (éstas son los términos indefinidos). Construir una geometría de esta manera exige que los significados de las palabras correspondientes a la primera clase se encuentren ya establecidos, en algún ámbito exterior a la geometría. Estas palabras forman un esqueleto rígido, que otorga una estructura subyacente al sistema; otro material es el encargado de rellenar el esqueleto, y puede ser de uno u otro tipo (de orientación euclidiana o no euclidiana).
Frecuentemente, los sistemas formales son construidos con arreglo a esta misma ordenación secuencial o jerárquica. Por ejemplo, se puede crear un Sistema Formal I, dotado de reglas y axiomas que den a sus símbolos los significados pasivos que se desean. Luego, el Sistema Formal I es incorporado en su totalidad a un sistema más amplio, dotado de mayor cantidad de símbolos: el Sistema Formal II. Como los axiomas y reglas del Sistema Formal I son parte del Sistema Formal II, los significados pasivos de sus símbolos siguen siendo válidos; forman un esqueleto inmutable que, a su vez, cumple una función muy importante en la determinación de los significados pasivos de los símbolos correspondientes al Sistema Formal II.
El segundo sistema puede, llegado su turno, llenar la función de esqueleto con respecto a un tercer sistema, y así sucesivamente. También es posible —y la geometría es una excelente muestra— contar con un sistema (por ejemplo, la geometría absoluta) que acote parcialmente los significados pasivos de sus términos indefinidos, y que pueda ser complementado con reglas y axiomas adicionales, los cuales harán una nueva acotación de los significados pasivos de los términos indefinidos. Esto es lo que ocurre en el enfrentamiento entre geometría euclidiana y no euclidiana.
Capas diferentes en la percepción visual
En una forma igualmente jerárquica adquirimos nuevos conocimientos, nuevo vocabulario, o percibimos objetos desacostumbrados. Esto se actualiza de modo interesante en el caso de la comprensión de obras de Escher, tales como Relatividad (figura 22), en la cual aparecen imágenes francamente imposibles. Uno piensa que habría que profundizar la interpretación del cuadro una y otra vez antes de arribar a una síntesis despojada de contradicciones… pero no procede así en absoluto. Uno se instala allí, divertido e intrigado por las escalinatas orientadas cada cual en su caprichosa dirección, y por las personas que marchan en contradictorias caminatas sobre una misma escalera. Aquellas escalinatas son “islas de certidumbre”, en las cuales basamos nuestra interpretación de toda la imagen. Una vez identificadas, tratamos de extender nuestra comprensión, buscando saber qué relación sustentan entre sí. Pero esta indagación tropieza con dificultades que limitan su avance; y si intentamos retroceder hacia las “islas de certidumbre” también tropezamos con dificultades, de otro género ahora. No hay manera de volver atrás y “ultradecidir” que aquéllas no son escalinatas. No son buzos, ni peces, ni balancines; son precisamente escalinatas. (En verdad, existe otra salida, consistente en dejar todas las líneas de la imagen sin interpretar en absoluto, como si fuesen “símbolos no significativos” de un sistema formal. Esta alternativa es un ejemplo de “vía U”, de actitud zen hacia lo simbólico).
En consecuencia, la naturaleza jerárquica de nuestros procesos perceptivos nos obliga a ver allí o bien un mundo alocado, o nada más que un grupo de líneas sin propósito. Una gran cantidad de obras de Escher puede suscitar análoga reflexión, obras que se fundan en la reconocibilidad de determinadas formas básicas, las cuales son vinculadas entre sí de maneras inhabituales: cuando el espectador capta la paradoja en su alto nivel, ya es demasiado tarde, pues no puede regresar y modificar la noción que ya adquirió acerca de cómo interpretar los objetos en el nivel inferior. La diferencia entre una imagen de Escher y la geometría no permiten obtener interpretaciones inteligibles, de las que emerge todo un sistema inteligible; dentro de la primera, en cambio, la conclusión final no es reconciliable con la concepción del mundo del espectador, por muy atenta y largamente que éste escudriñe el cuadro. Por supuesto, uno puede elaborar mundos hipotéticos, donde los sucesos escherianos sean factibles… pero en estos mundos, las leyes biológicas, físicas, matemáticas e inclusive las lógicas, son violadas en un nivel, y al mismo tiempo respetadas en otro, lo cual los convierte en mundos sumamente fantásticos. (Como lo muestra Cascada (figura 5), donde la fuerza de gravedad impulsa normalmente el agua, pero la naturaleza del espacio circundante infringe las leyes de la física).

FIGURA 22. Relatividad (litografía, 1953).
¿La matemática sigue siendo la misma en cualquier mundo concebible?
Hemos subrayado el hecho, líneas atrás, de que la coherencia interna de un sistema formal (acompañado por una interpretación) requiere que haya algún mundo imaginable —es decir, un mundo cuya única restricción consista en que la matemática y la lógica sean las mismas de nuestro mundo—, donde todos los teoremas interpretados resulten verdaderos. La coherencia externa —la coherencia con el mundo externo— requiere, en cambio, que todos los teoremas resulten verdaderos en el mundo real. Ahora bien, en el caso especial de que se desee crear un sistema formal coherente cuyos teoremas tengan que ser interpretados como proposiciones matemáticas, pareciera que la diferencia entre ambos tipos de coherencia tiende a disiparse ya que, de acuerdo a lo dicho anteriormente, todos los mundos imaginables tienen la misma matemática que el mundo real. Así, en cualquier mundo que queramos concebir, 1 más 1 deberá ser 2; también tendrá que haber infinitos números primos, y todos los ángulos rectos serán congruentes. Del mismo modo, por supuesto, a través de un punto exterior a una recta podrá pasar exclusivamente una paralela…
Pero, ¡un momento! Éste es el postulado de las paralelas, y afirmar su universalidad sería un error, a la luz de lo que precisamente acabamos de decir. Si sustentamos el postulado de las paralelas en todos los mundos concebibles, estamos afirmando así que la geometría no euclidiana es inconcebible, con lo cual nos retrotraemos a la misma actitud conceptual de Saccheri y de Lambert: un paso nada sabio, por cierto. ¿Pero entonces qué es lo que deben compartir todos los mundos concebibles, si no es toda la matemática? ¿Sería algo tan reducido como la lógica?, ¿o también hay que desconfiar de la lógica? ¿Podrá haber mundos donde las contradicciones sean una parte normal de la existencia: mundos donde las contradicciones no sean contradicciones?
Bien, en cierto sentido y por el solo hecho de haber inventado el concepto, hemos mostrado que tales mundos son perfectamente concebibles; no obstante, en un sentido más profundo, son a la vez por entero inconcebibles (lo cual configura una pequeña contradicción). Pero hablando con seriedad, pareciera que si queremos ser capaces de comunicamos, debemos adoptar una base común, y aquí tiene que ser incluida la lógica. (Hay sistemas de creencias que rechazan este punto de vista, por excesivamente lógico. En particular, el zen acoge las contradicciones y las no contradicciones con la misma estimación. Esto puede parecer incoherente, pero en ese caso la incoherencia es parte del zen, y entonces… ¿qué puede uno decir?).
¿La teoría de los números sigue siendo la misma en cualquier mundo concebible?
Si suponemos que la lógica es parte de cualquier mundo concebible (no hemos dado aún una definición de “lógica”, pero lo haremos en los próximos capítulos), ¿bastará con eso? ¿Es verdaderamente concebible que, en algunos mundos, no haya un número infinito de primos? ¿No sería necesario que los números respondieran a las mismas leyes en todos los mundos imaginables? ¿O… no será mejor considerar al concepto de “número natural” como un término indefinido, análogo a “PUNTO” o a “LINEA”? De ser así, la teoría de los números debería escindirse, como la geometría, de modo que haya teorías corrientes de los números y teorías no corrientes. Pero debería existir, para ello, un correlato de la geometría absoluta: una “esencia” teórica, un ingrediente invariante de todas las teorías de los números, que las identifique como teorías de los números y no como, digamos, teorías acerca del cacao, el caucho o los plátanos. Parece haber consenso dentro de la mayoría de los matemáticos y filósofos contemporáneos en el sentido de que hay tal esencialidad en la teoría de los números, la cual debería ser incluida, junto con la lógica, dentro de lo que calificamos como “mundos concebibles”. Esta esencia de la teoría de los números, este correlato de la geometría absoluta, es la llamada aritmética de Peano, y nosotros la formalizaremos en el Capítulo VIII. Además, ya se encuentra bien establecido —como cuestión de hecho, y como consecuencia directa del Teorema de Gödel— que la teoría de los números es una teoría escindida en versiones comentes y no corrientes. A diferencia de lo que ocurre en la geometría, sin embargo, la cantidad de variantes de teorías de los números es infinita, de lo que se deriva una situación notablemente más compleja.
Para fines prácticos, todas las teorías de los números son la misma. Es decir que si la construcción de un puente depende de la teoría de los números (lo cual, en cierto sentido, es así), el hecho de que haya diferentes teorías de los números no viene al caso pues, en los aspectos que atañen al mundo real, todas aquellas coinciden. No se puede decir lo mismo de las distintas geometrías; por ejemplo, la suma de los ángulos de un triángulo da como resultado 180 grados solamente dentro de la geometría euclidiana; la suma es mayor dentro de la geometría elíptica, y menor dentro de la hiperbólica. Se cuenta que Gauss, en una oportunidad, intentó obtener la suma de los ángulos de un gran triángulo descrito por los picos de tres montañas, con la finalidad de determinar, de una vez y para siempre, qué clase de geometría rige verdaderamente nuestro universo. Cien años más tarde, Einstein formuló una teoría (la de la relatividad generalizada), según la cual la geometría del universo es determinada por la materia que éste contiene; en consecuencia, ninguna geometría es intrínseca al espacio mismo. De tal modo, la pregunta “¿Qué geometría es verdadera?” recibe de la naturaleza una respuesta ambigua no sólo en el ámbito de la matemática, sino también en el de la física. En cuanto a la pregunta correlativa, “¿Qué teoría de los números es verdadera?” tendremos más para decir, luego de recorrer en detalle el Teorema de Gödel.
Completitud
Si la coherencia es la condición mínima bajo la cual los símbolos adquieren significados pasivos, su noción complementaria, la de completitud, actúa como ratificación máxima de esos significados. La coherencia es el atributo consistente en que “Todo lo producido por el sistema es verdadero”, en tanto la completitud da un giro: “Toda proposición verdadera es producida por el sistema”. Vamos a desarrollar un poco estos conceptos. No estamos hablando de todas las proposiciones verdaderas del mundo, sino exclusivamente de las pertenecientes al dominio que queremos representar a través del sistema. Luego» la completitud establece: “Toda proposición verdadera que puede ser expresada en la notación del sistema es un teorema”.
- Coherencia:
- cuando los teoremas, al ser interpretados, resultan verdaderos (en algún mundo imaginable).
- Completitud:
- cuando todas las proposiciones que son verdaderas (en algún mundo imaginable), y que pueden ser expresadas como cadenas bien formadas del sistema son teoremas.
Un ejemplo de sistema formal completo, en su modesto nivel, lo constituye el sistema mg original, con su interpretación inicial. Todas las sumas verdaderas de dos enteros positivos son representadas por teoremas del sistema. Podemos formularlo de este otro modo: “Todas las sumas verdaderas de dos enteros positivos son demostrables dentro del sistema”. (Atención: cuando comenzamos a emplear la expresión “proposiciones demostrables” en lugar de “teoremas”, ello muestra que hemos dejado de distinguir nítidamente entre sistemas formales y sus interpretaciones. Esto es correcto, siempre que seamos conscientes de la ambigüedad que se está insinuando, y que recordemos que a veces es posible la existencia de interpretaciones múltiples). El sistema mg con su interpretación original es completo; es, también, coherente, puesto que ninguna proposición falsa —para usar nuestra nueva expresión— es demostrable dentro del sistema.
Alguien podría sostener que el sistema es incompleto, sobre la base de que la suma de tres enteros positivos (tales como 2 + 3 + 4 = 9) no es representada por los teoremas del sistema mg, aun siendo traducible a la notación del sistema (por ejemplo, --m---m----g---------). Empero, esta cadena no está bien formada, y tiene que ser considerada tan carente de significado como mgm---gmg. La suma triple, sencillamente, no es formulable en la notación del sistema, por lo que la completitud del mismo se mantiene inalterada.
A pesar de ello, el sistema mg carece ciertamente de alcances como para capturar la noción íntegra de verdad correspondiente a la teoría de los números. Por ejemplo, no hay manera de que el sistema mg nos diga cuántos números primos hay. El Teorema de la Incompletitud, de Gödel, dice que cualquier sistema que sea “suficientemente poderoso” es, en virtud de su mismo poder, incompleto, pues hay cadenas bien formadas que enuncian proposiciones verdaderas de teoría de los números, pero no son teoremas. (Hay verdades pertenecientes a la teoría de los números que no son demostrables dentro del sistema). Sistemas como el mg, completos pero no muy poderosos, se asemejan a los fonógrafos de baja fidelidad. Son, sobre todo, tan limitados, que obviamente no pueden cumplir con lo que nosotros desearíamos, a saber, que nos digan todo a propósito de la teoría de los números.
Cómo la incompletitud puede ser hecha o deshecha por una interpretación
¿Qué queremos decir con aquello de que “la completitud es la ratificación máxima de los significados pasivos”? Lo siguiente: que si un sistema es coherente, pero incompleto, hay un desajuste entre los símbolos y su interpretación. El sistema carece del poder suficiente para dar validez a esa interpretación. En ocasiones, si las interpretaciones son “acicaladas” un poco, el sistema puede devenir completo. Esto puede ser ilustrado por el sistema mg modificado (incluyendo el esquema de axioma II) y la interpretación que le aplicamos.
Después de modificar el sistema mg, modificamos la interpretación de g: sustituimos “igual a” por “es mayor que o igual a”. Vimos que el sistema mg modificado adquiría coherencia bajo esta interpretación, pero hay algo en esta última que no es enteramente satisfactorio. El problema es simple: existen ahora muchas verdades expresables que no son teoremas; por ejemplo, “2 más 3 es mayor que o igual a 1” es expresado por el no teorema --m---g-. ¡Es una interpretación demasiado desmañada! No refleja con exactitud las posibilidades de los teoremas del sistema. Bajo esta desmañada interpretación, el sistema mg no es completo. Podríamos hacer un reajuste, a través de (1) el agregado de nuevas reglas al sistema, que lo hagan más poderoso, o bien de (2) la restricción interpretativa. En nuestro caso, la alternativa más sensata es esta última, aparentemente, de manera que en lugar de interpretar g como “es mayor que o igual a”, diríamos “es igual o supera por 1”. Ahora sí el sistema mg modificado adquiere coherencia y completitud, y esta última ratifica el carácter adecuado de la interpretación.
La incompletitud en la teoría de los números formalizada
Dentro de la teoría de los números, volvemos a tropezar con la incompletitud; y aquí, para remediar la situación, hay que tomar otro camino: el del agregado de nuevas reglas, que hagan más poderoso al sistema. Pero aparece la ironía de que, cada vez que incorporamos una nueva regla, nos sentimos seguros de que ahora sí el sistema es completo. La naturaleza del dilema puede ser manifestada por la siguiente alegoría…
Tenemos un fonógrafo, y un disco experimentalmente rotulado “Canon en B-A-C-H”. Sin embargo, cuando queremos escuchar el disco mediante el fonógrafo, las vibraciones producidas por retroalimentación (similares a las causadas por los discos de la Tortuga) interfieren tanto que ni siquiera conseguimos distinguir la melodía. Concluimos entonces que algo falla: o el disco o el fonógrafo. Para probar el primero, tendríamos que ponerlo en el fonógrafo de un amigo y verificar su calidad; para probar el segundo, tendríamos que poner en él otros discos y verificar si la música que escuchamos concuerda con los rótulos. Si nuestro fonógrafo aprueba su examen, diremos que la falla está en el disco y, en caso contrario, diremos que la falla está en el fonógrafo. Pero, ¿qué diremos si ambos aprueban sus respectivos exámenes? ¡Será el momento de recordar el encadenamiento de dos isomorfismos (figura 20), y meditar cuidadosamente!


