LA IDEA DE QUE LOS CONCEPTOS pueden ser capturados por la sola acción de manipulaciones tipográficas despierta la curiosidad. El único concepto aprehendido hasta ahora ha sido el de adición, lo cual puede no haber parecido muy extraño. Supongamos, en cambio, que se planeara crear un sistema formal con teoremas de la forma Px, donde la letra ‘x’ representa una cadena de guiones; en tales teoremas, la cadena de guiones deberá contener necesariamente un número primo de guiones. Así, P--- será un teorema, y P---- no lo será. ¿Cómo se podrá expresar esto tipográficamente? Primero, es importante especificar con claridad qué quiere decir operaciones tipográficas. El repertorio completo ha sido presentado junto con los sistemas MIU y mg, de manera que ahora necesitamos solamente elaborar la lista de las posibilidades que hemos permitido:

El inventario es algo redundante, pero no hay inconveniente en ello. Lo que importa señalar es que solamente convoca capacidades triviales, todas ellas inferiores a las necesarias para distinguir entre números primos y no primos. ¿Cómo haremos, entonces, para emplear algunas de esas operaciones en la construcción de un sistema formal donde los números primos y los números compuestos son diferenciados entre sí?

El sistema vg

El primer paso sería tratar de resolver un problema más simple, pero relacionado con la pregunta anterior. Tendríamos que intentar la construcción de un sistema similar al mg, pero para representar la multiplicación y ya no la suma. Lo llamaremos sistema tg: ‘v’ quiere decir ‘veces’. Más detalladamente, supongamos que X, Y y Z son, respectivamente, el número de guiones en las cadenas de guiones x, y y z. (Obsérvese que adopto especial cuidado en distinguir entre una cadena y el número de guiones que la misma contiene). Luego, establecemos que la cadena xvygz es un teorema si, y sólo si, X veces Y es igual a Z. Por ejemplo, --v---g------ sería un teorema porque 2 veces 3 es igual a 6, pero --v--g--- no lo sería. El sistema vg puede ser caracterizado casi tan fácilmente como el mg, es decir, mediante un solo esquema de axioma y una regla de inferencia:

REGLA DE INFERENCIA: Supongamos que x, y y z son todas cadenas de guiones. Y supongamos que xvygz es un teorema conocido. Luego, xvy-gzx será un nuevo teorema.

Advirtamos cómo crece la cadena central, a razón de un guión por cada oportunidad en que es aplicada la regla de inferencia; de tal forma, si se desea obtener un teorema con diez guiones en el centro, es previsible que haya de aplicarse nueve veces la regla de inferencia, dentro de esa serie.

La captura de la compositividad

Acabamos de “capturar” tipográficamente a la multiplicación, concepto éste sólo ligeramente más complejo que el de la suma: su captura se parece a la de los pájaros, en Liberación, de Escher. ¿Cómo haremos con la primidad? He aquí un plan que puede considerarse astuto: emplear el sistema vg para definir un nuevo conjunto de teoremas de la forma Cx, la cual caracterizará a los números compuestos. Veamos:

REGLA: Supongamos que x, y y z cadenas de guiones. Si x-vy-gz es un teorema, entonces Cz también es un teorema.

Debe indicarse que Z (el número de guiones de z) es un compuesto que equivale al producto de dos números mayores que 1, a saber, X + 1, e Y + 1 (X e Y son el número de guiones de x e y, respectivamente). Voy a fundamentar esta regla aportando algunas argumentaciones del tipo “vía inteligente”, puesto que el lector es un ser humano, y requiere saber por qué elaboro dicha regla. Si la actitud fuera de no abandonar los límites de la “vía mecánica”, no haría falta justificación alguna, pues los seguidores de la vía M obedecen mecánica y complacidamente las reglas, sin cuestionarlas jamás.

A causa de que la actitud del lector responde a la vía I, tenderá a confundir la distinción entre cadenas y sus interpretaciones. Está a la vista que las cosas pueden presentarse sin ninguna claridad tan pronto como se percibe que hay “significación” en los símbolos que se están manipulando. El lector, con seguridad, tiene que luchar consigo mismo para no pensar que la cadena ‘---’ es el número 3. El Requisito de Formalidad, que probablemente impresionara como enigmático en el Capítulo I (por ser tan obvio), se volverá ahora complejo y concluyente. Es esencial guardarse de mezclar la vía I con la vía M; o, en otros términos, es esencial no confundir los hechos de la aritmética con los teoremas tipográficos.

Caracterización ilegítima de primos

Es sumamente tentador brincar desde los teoremas del tipo C, directamente, a los del tipo P, mediante la proposición de una regla del siguiente género:

REGLA PROPUESTA: Supongamos que x es una cadena de guiones. Si Cx no es un teorema, entonces Px es un teorema.

La falla insoluble, aquí, es que la verificación de si Cx no es un teorema no constituye una operación expresamente tipográfica. Para saber a ciencia cierta que MU no es un teorema del sistema MIU, es imprescindible salir del sistema… y lo mismo ocurre con la Regla Propuesta. Se trata de una regla que viola en su totalidad la noción de sistema formal, desde el momento que nos exige operar informalmente, o sea, fuera del sistema. La operación tipográfica (6) nos permite examinar la colección de teoremas descubiertos, mientras que la Regla Propuesta nos requiere que inspeccionemos una hipotética “Tabla de no teoremas”. Ahora bien, si queremos elaborar esta tabla, tenemos que conducir ciertos razonamientos fuera del sistema: razonamientos que muestren la causa por la cual algunas cadenas no pueden ser producidas dentro del sistema. Pero bien podría ser que hubiese otro sistema formal facultado para generar la “Tabla de no teoremas”, por medio de recursos exclusivamente tipográficos. En realidad, nuestro propósito es descubrir un sistema semejante; ya que la Regla Propuesta no es una regla tipográfica, debe ser desestimada.

Este aspecto es de tal importancia que conviene extendernos un poco más a su respecto. En nuestro sistema C (el cual incluye el sistema vg y la regla que define los teoremas del tipo C), tenemos teoremas de la forma Cx, donde ‘x’ representa, como siempre, una cadena de guiones. También hay no teoremas de la forma Cx (a ellos aludo cuando digo “no teoremas”, si bien vv-Cgg u otras revolturas caprichosas son también no teoremas). La diferencia reside en que los teoremas tienen un número compuesto de guiones, y los no teoremas tienen un número primo de guiones. Por otra parte, todos los teoremas cuentan con una “forma” común, porque son generados por un mismo conjunto de reglas tipográficas. Luego, ¿tendrán asimismo los no teoremas una “forma” común, por análogas razones? Más abajo aparece una lista de teoremas del tipo C, enunciados sin sus derivaciones; los números entre paréntesis representan simplemente la suma de los guiones que corresponden a cada teorema:

Los “huecos” de la lista son los no teoremas. Podemos parafrasear la pregunta anterior: ¿los huecos tienen una “forma” común?, y agregar: ¿sería razonable sostener que, sólo por tratarse de los huecos de esta lista, comparten una forma común? Sí y no. Que comparten cierta cualidad tipográfica es innegable, pero no lo es la posibilidad de llamar “forma” a esa cualidad. La incertidumbre se funda en que los huecos están definidos de manera exclusivamente negativa: son las cosas que han sido descartadas en la confección de una lista definida positivamente.

Figura y fondo

Esto recuerda la célebre distinción artística entre figura y fondo. Cuando una figura o “espacio positivo” (sea una forma humana, una letra, o una naturaleza muerta) es trazada en el interior de un marco determinado, se produce la inevitable consecuencia de que también queda trazada su forma complementaria —llamada otras veces “fondo”, “trasfondo” o “espacio negativo”—. Sin embargo, en la mayoría de los diseños la relación figura-fondo juega un papel menor; el artista se interesa mucho más por la figura que por el fondo. Pero hay ocasiones en que el artista presta atención a este último.

Existen hermosos alfabetos cuya eficacia se basa en la distinción figura-fondo. Poco más abajo se muestra un mensaje escrito en un alfabeto semejante; al principio se creería que es una hilera de algo parecido a gotas caprichosas, pero si uno retrocede por etapas y se va fijando con atención, súbitamente se verán aparecer siete letras…

Un efecto análogo podrá observarse en mi dibujo Señal de fumar (figura 139). Siguiendo sus líneas, puede considerarse este acertijo: ¿es posible elaborar, de un modo u otro, un dibujo que contenga palabras en la figura y en el campo?

Haremos ahora una distinción canónica entre dos clases de figuras: las que se trazan cursivamente, y las recursivas (quizá es del caso aclarar que se trata dé categorías que me pertenecen; no son del uso común). Una figura cursiva es aquella cuyo campo aparece tan sólo como subproducto del acto de dibujar. Una figura recursiva, en cambio, es aquella cuyo fondo puede ser visto, por derecho propio, como una figura. Generalmente, es el artista en forma plenamente deliberada quien otorga esta relevancia al fondo. El “re” de “recursivo” expresa el hecho de que tanto el primer plano como el plano posterior, o fondo, son trazables en forma cursiva: la figura es “doblemente cursiva”. El límite entre figura y fondo, en una figura recursiva, es una espada de doble filo. M. C, Escher fue un maestro en materia de figuras recursivas, como se aprecia, por ejemplo, en su bello dibujo recursivo de pájaros mostrado en la figura 16.

FIGURA 16. Cobertura de un plano mediante pájaros, de M. C. Escher (de un cuaderno de apuntes, 1942).

Nuestra distinción no es tan rigurosa como las de la matemática, porque, ¿quién puede afirmar concluyentemente que un fondo en particular no es una figura? Una vez que se le ha prestado atención, casi cualquier fondo gana interés por sí mismo. En tal sentido, no hay figura que no sea recursiva; pero no es éste el alcance que le doy al término: hay una noción intuitiva y natural que permite el reconocimiento de formas; entonces, el primer plano y el fondo ¿son ambos formas reconocibles? Si es así, la imagen es recursiva. Si observamos los campos de la mayoría de los diseños de tipo técnico, nos resultarán irreconocibles. Esto demuestra que:

Existen allí formas reconocibles, cuyo espacio negativo no es una forma reconocible cualquiera.

Creo que la Figura FIGURA-FIGURA, de Scott Kim, mostrada en la figura 17, responde a la pregunta que planteamos. Si nos fijamos al mismo tiempo en las zonas blancas y en las negras, veremos “FIGURA” en todas partes, ¡y “FONDO” en ninguna! Es un paradigma de figura recursiva. En este talentoso diseño, hay dos recursos no equivalentes de caracterización de las zonas negras:

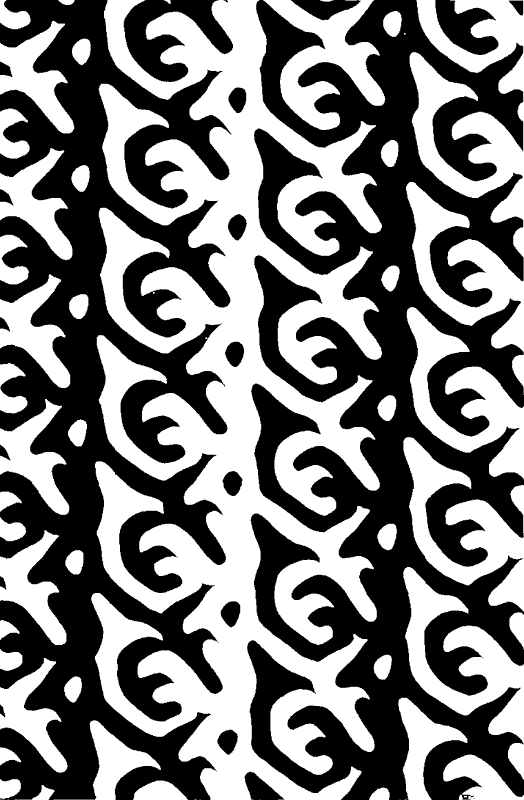
FIGURA 17. Figura FIGURA-FIGURA, de Scott E. Kim (1975).

(En el caso especial de Figura FIGURA-FIGURA, ambas caracterizaciones son equivalentes; pero en la mayoría de las pinturas en blanco y negro no lo son). En el Capítulo VIII formulamos nuestra Teoría de los Números Tipográfica (TNT): confiamos en que nos permita caracterizar de forma análoga al conjunto de todas las proposiciones falsas de teoría de los números, es decir:

Ya veremos cómo y por qué ocurre esto, en el Capítulo XIV. Entretanto, analicemos la representación gráfica de la situación que exhibe la figura 18.

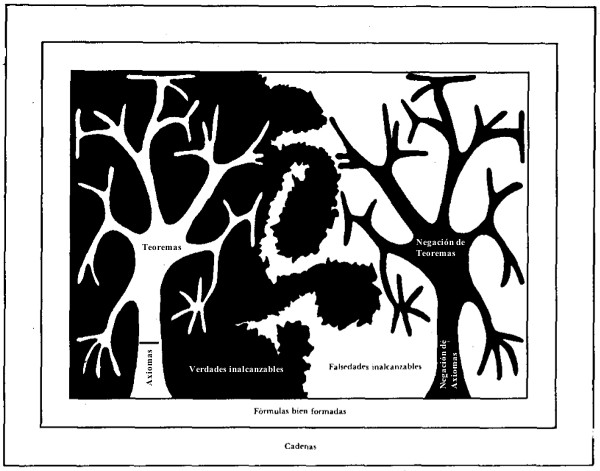
FIGURA 18. Este diagrama de las relaciones existentes entre las diversas clases de cadenas TNT concentra un grado considerable de simbolismo visual. El rectángulo mayor representa el conjunto de todas las cadenas TNT; el que lo sigue en tamaño, el conjunto de todas las cadenas TNT bien formadas. Dentro de éste se encuentra el conjunto de todos los enunciados de TNT. Ahora las cosas se ponen interesantes. El conjunto de los teoremas es dibujado en forma de árbol, cuyo tronco representa el conjunto de los axiomas. El árbol símbolo fue adoptado a causa del modelo de crecimiento recursivo que exhibe: ramas nuevas (los teoremas) que se gestan constantemente a partir de las más viejas. Las ramas delgadas sondean los rincones de la región comprimida (el conjunto de verdades,), pero nunca los podrán ocupar por completo. La frontera divisoria entre el conjunto de verdades y el conjunto de falsedades ha sido diseñada para sugerir una costa caprichosamente serpenteada; por más detalladamente que se la examine, siempre aparecerán en ella niveles estructurales más sutiles, por lo que resulta imposible describirla con exactitud aplicando métodos finitos (véase el libro de B. Mandelbrot, Fractals). El árbol en negro representa el conjunto de negaciones de teoremas; éstos, pese a ser falsos en su totalidad, no pueden cubrir, como conjunto, el espacio de los enunciados falsos. [Dibujo del autor.]

Figura y fondo en música

También se pueden buscar figuras y fondos en la música, donde melodía y acompañamiento se relacionan de modo análogo, ya que la melodía está siempre en el primer plano de nuestra atención, mientras que el acompañamiento, de algún modo, es secundario. De aquí que resulte sorprendente encontrar a veces, en las líneas menos audibles de una pieza musical, melodías reconocibles. Esto no ocurre demasiado a menudo en la música posterior a la barroca. Por lo general, los elementos armónicos no son considerados de primer plano, pero dentro de la música barroca —en Bach, sobre todo— las distintas líneas actúan como “figuras”, ya sean altas, bajas o intermedias. En este sentido, las composiciones de Bach pueden ser denominadas “recursivas”.

Existe otra distinción figura-fondo en música: la que encontramos entre “tiempos” y “contra-tiempos”. Si uno cuenta las notas mediante la pauta “uno-y, dos-y, tres-y, cuatro-y”, la mayor parte de las notas melódicas coincidirán con los números. Pero en ocasiones una melodía es desplazada hacia las “y” buscando un efecto distinto, como sucede en algunos estudios para piano de Chopin. Esto también se aprecia en Bach, sobre todo en sus Sonatas y Partitas para violín solo, y en sus Suites para violoncelo solo. En estas composiciones, Bach logra que dos o más líneas musicales avancen de manera simultánea; lo consigue, en ciertas oportunidades, haciendo que el instrumento a cargo del solo realice “acordes”, es decir, dos notas por tiempo; en otras, ubica una voz sobre los tiempos, y la otra voz sobre los contra-tiempos, así el oído las separa, y oye dos melodías diferentes que se entrelazan, se distancian, y en todo momento armonizan, entre sí. No hace falta decir que Bach no se detuvo en este nivel de complejidad…

Conjuntos recursivamente enumerables vs. conjuntos recursivos

Vamos a llevar ahora las nociones de figura y fondo al dominio de los sistemas formales. En nuestro ejemplo, la función de espacio positivo es cumplida por los teoremas del tipo C, y la de espacio negativo por cadenas con un número primo de guiones. Hasta ahora, el único medio que hemos encontrado para representar números primos tipográficamente ha sido concebirlos como un espacio negativo. Sin embargo, ¿no habrá alguna forma, así sea muy complicada, de representar a los primos como un espacio positivo, esto es, como conjunto de teoremas de un sistema formal?

Diferentes intuiciones dan diferentes respuestas a esto. Recuerdo muy bien la perplejidad y la intriga en que me había sumido mientras estudiaba la distinción entre caracterización positiva y caracterización negativa. Yo estaba completamente convencido de que no sólo los primos, sino cualquier conjunto de números que pudiese ser representado negativamente, también podía ser representado positivamente. Mi convencimiento se fundaba en una intuición que es sintetizada por la pregunta: ¿cómo es posible que una figura y su fondo no contengan la misma información?”. Para mí, ambos incluían la misma información, aunque codificada de dos maneras complementarias. ¿Era una respuesta correcta?

Resultó que yo estaba acertado acerca de los primos, pero equivocado en general, lo cual me asombró, y continúa asombrándome todavía hoy. No se discute que:

Existen sistemas formales cuyo espacio negativo (conjunto de no teoremas) no es el espacio positivo (conjunto de teoremas) de ningún sistema formal.

Esta conclusión manifiesta una profundidad similar a la del Teorema de Gödel, de modo que no es sorprendente que mi intuición se frustrase. Igual que los matemáticos de comienzos de este siglo, yo contaba con que el mundo de los sistemas formales y el de los números naturales se mostrasen más previsibles de lo que son. Para decirlo con terminología más técnica:

La expresión recursivamente enumerable (frecuentemente abreviada “r. e.”) es el correlato matemático de nuestra noción artística de “cursivamente trazable”, y recursivo es el correlato de “recursivo”. Que un conjunto de cadenas sean “r. e.” significa que pueden ser generadas mediante la aplicación de reglas tipográficas: el conjunto de los teoremas del tipo C, el conjunto de los teoremas del sistema MIU, por ejemplo, y por supuesto el conjunto de teoremas de cualquier sistema formal. Esto es comparable con una concepción de “figura” como “conjunto de lineas que pueden ser generadas mediante la aplicación de reglas artísticas” (¡sea lo que fuere lo que se entienda por esto!). Y un “conjunto recursivo” es como una figura cuyo fondo es también una figura: es r. e., pero su complemento también es r. e.

Existen sistemas formales para los que no hay procedimiento tipográfico de decisión.

¿Cómo se llega a esto? Muy fácilmente. Un procedimiento tipográfico de decisión es un método que distingue entre teoremas y no teoremas. Su existencia nos permite producir sistemáticamente todos los no teoremas, mediante el simple recurso de enumerar todas las cadenas y someterlas al procedimiento verificador, una por una, descartando las cadenas y teoremas mal formados. Esto equivale a disponer de un método tipográfico de producción del conjunto de no teoremas. Pero según lo enunciado anteriormente (y en este momento le daremos plena fe), ello no es posible en algunos sistemas. Luego, debemos concluir que no todos los sistemas formales cuentan con procedimientos tipográficos de decisión.

Supóngase que tenemos un conjunto I de números naturales (‘I’ representa a ‘Figura’) —los números compuestos, por ejemplo—, a los que pudiéramos generar mediante algún método formal. Supongamos que su complemento es el conjunto O (‘O’ representa a ‘Fondo’) —los números primos, por ejemplo—. Juntos, I y O abarcan todos los números naturales, y conocemos una regla que nos permite producir todos los números del conjunto I, pero no conocemos ninguna similar para producir los números del conjunto O. Es importante fijarse en que, sí los miembros de I fueran generados siempre en orden creciente, podríamos en todo momento caracterizar a O. El problema es que muchos conjuntos r. e. son generados a través de métodos que diseminan los elementos en un orden arbitrario, así que nunca se sabe si un número omitido largo tiempo obtendrá, esperando un poco más, su inclusión.

A la pregunta “¿son recursivas todas las figuras?” respondimos negativamente, en el plano artístico. Ahora vemos que la respuesta también debe ser negativa en el plano de la matemática, cuya pregunta se formula así: “¿son recursivos todos los conjuntos?”. Desde esta perspectiva, volvamos a la elusiva palabra “forma”: observando de nuevo nuestro conjunto-figura I y nuestro conjunto-fondo O, podemos convenir en que todos los números del conjunto I tienen cierta “forma” común, pero, ¿puede decirse lo mismo de los números del conjunto O? Es un problema curioso. Cuando estamos comenzando a abordar un conjunto infinito —el de los números naturales—, los vacíos creados por el desplazamiento de algún subconjunto pueden ser muy difíciles de definir explícitamente. Pudiera ser, entonces, que no estén vinculados por ningún atributo o “forma” común. En último caso, usar la palabra “forma” es cuestión de preferencia personal, siempre que se recuerden sus facetas problemáticas. Quizá sea mejor no definir “forma”, sino dejarla un tanto librada a la fluidez de las intuiciones.

Y a continuación, planteo un acertijo relacionado con los temas recién examinados: ¿Cómo se puede caracterizar el conjunto de enteros (o su espacio negativo) que sigue?

Los primos: figura, no fondo

En definitiva, ¿qué decir acerca de un sistema formal para la producción de números primos?, ¿cómo construirlo? El ardid consiste en brincar por encima de la multiplicación, y recurrir directamente a la no divisibilidad para su representación positiva. Tenemos aquí un esquema de axioma y una regla para la generación de teoremas, los cuales manifiestan el hecho de que un número demostradamente no divide (DND) a otro en forma exacta.

Por ejemplo, -----DND--, dónde x ha sido remplazado por ‘--’ e y por ‘---’.

que corresponde interpretar como “5 no divide a 12”. Sin embargo, ---DND------ no es un teorema, ¿dónde está la equivocación si tratamos de producirlo?

Ahora bien, para determinar que un número dado es primo debemos poseer algunos conocimientos acerca de sus propiedades de no divisibilidad. En particular, tenemos que saber que no es divisible por 2, ni por 3, ni por 4, etc., hasta el número inferior en 1 al número dado. Pero en el ámbito de los sistemas formales no podemos decir, tan ambiguamente, “etcétera”, sino que debemos formular algo concreto. Sería bueno contar con una forma de decir, en el lenguaje del sistema, “el número Z está exento de divisores hasta X”, para significar que ningún número entre 2 y X divide a Z. Esto se puede lograr, aunque a costa de una triquiñuela. Piénselo el lector, si le interesa.

REGLA: Si zEDx es un teorema, y también x-DNDz es un teorema, entonces zEDx- es un teorema.

Estas dos reglas capturan la noción de exención de divisor. Todo lo que necesitamos hacer es decir que los primos son números exentos de divisor hasta 1 menos que ellos mismos:

Y ya está. El fundamento de la representación formal de la primidad consiste en que hay una prueba de la divisibilidad, que puede ser practicada sin necesidad de volver atrás. Marchamos constantemente hacia adelante, verificando primero la divisibilidad por 2, luego por 3, y así siguiendo. Es la “monotonicidad” o unidireccionalidad del método —la ausencia de toda interacción entre ampliación y reducción, o entre incremento y decremento— lo que permite que la primidad sea aprehendida. Esta compleja capacidad de los sistemas formales para desarrollar y acumular interferencias arbitrarias que operan en distintas direcciones es la causa de tan pobres resultados como el Teorema de Gödel, el Problem de la Detención de Turing, y de que no todos los conjuntos recursivamente enumerables sean recursivos.

CAPÍTULO III