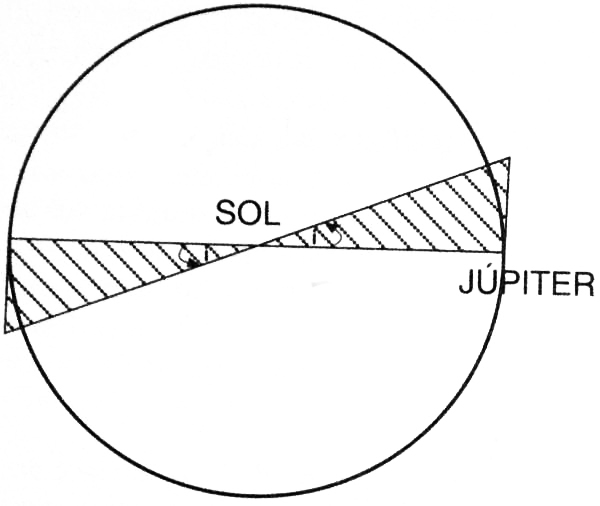
Volumen en forma de cuña ocupado por el cometa de Velikovsky.
Aspectos sencillos de la física de las colisiones; discusión de la probabilidad de una reciente colisión entre la Tierra y un miembro masivo del sistema solar.
Se considera aquí la probabilidad de que un objeto masivo expulsado por Júpiter del tipo considerado por Velikovsky choque con la Tierra. Velikovsky propone que ese cometa pasó rozando o muy cerca de la Tierra. En todo lo que sigue subsumiremos esta idea en la designación «colisión». Sea un objeto esférico de radio R que se desplace por una región en la que haya otros objetos de tamaño parecido. Se producirá una colisión cuando los centros de los objetos estén separados por una distancia 2R. Se puede hablar de una sección eficaz de colisión de σ = π(2R)2 = 4 π R2; esta es el área del blanco que debe encontrar el centro del objeto en movimiento para que se produzca una colisión. Supongamos que sólo se mueve uno de estos objetos (el cometa de Velikovsky) y que los demás (los planetas del sistema solar interior) están en estado estacionario. Al no considerar el movimiento de los planetas del sistema solar interno se introducen errores inferiores a un factor 2, como puede demostrarse fácilmente. Llamemos v a la velocidad del cometa y n a la densidad espacial de blancos potenciales (los planetas del sistema solar interno). Las unidades que utilizaremos para R serán los centímetros (cm); mediremos σ en cm2, v en cm/s y n en planetas por cm3 (evidentemente n es un número muy pequeño).
Aun a pesar de que la gama de inclinaciones orbitales respecto al plano de la eclíptica es muy extensa en los cometas, tomaremos el punto de vista que resulta más generoso para la hipótesis de Velikovsky y adoptaremos como valor de la inclinación el menor posible. Si no hiciésemos ninguna restricción a la inclinación orbital del planeta, tendría igual probabilidad de estar en cualquier punto de una esfera centrada en el Sol y de radio r = 5 unidades astronómicas (1 u.a. = 1,5 × 1013 cm), el semieje mayor de la órbita de Júpiter. Cuanto mayor es el volumen en el que puede moverse el cometa, menor es la probabilidad de que colisione con cualquier otro objeto. Debido a la rápida rotación de Júpiter, cualquier objeto eyectado desde el interior de este planeta, tendrá tendencia a desplazarse en el plano ecuatorial del planeta, que presenta una inclinación de 1,2° respecto al plano de revolución de la Tierra alrededor del Sol. Sin embargo, para que el cometa consiga llegar a la parte interna del sistema solar es necesario que la eyección haya sido lo suficientemente enérgica como para que su inclinación orbital, i, tome cualquier valor. Así, una cota inferior generosa es i = 1,2°. Consideraremos, por tanto, que el cometa se mueve (véase el diagrama) en una órbita contenida en un volumen en forma de cuña y centrado en el Sol (la órbita del cometa ha de tener al Sol en uno de sus focos) y de semiángulo i. Este volumen es de (4/3) π r3 sen i = 0,0296 × 1040 cm3, tan sólo el 2 por 100 del volumen de una esfera de radio r. Como en ese volumen hay tres o cuatro planetas (sin tener en cuenta los asteroides), la densidad espacial de blancos que se ajusta a nuestro problema es de unos 10-40 planetas/cm3. Una velocidad relativa típica de un cometa o de cualquier otro objeto que se mueva según una órbita excéntrica en el sistema solar interno es del orden de unos 20 km/s. El radio de la Tierra es R = 6,3 × 108 cm, que viene a ser también muy aproximadamente el radio del planeta Venus.

Volumen en forma de cuña ocupado por el cometa de Velikovsky.
Supongamos ahora que enderezamos la trayectoria elíptica del cometa y que T es el tiempo que transcurre hasta colisionar con un planeta. Durante ese tiempo habrá barrido un túnel de volumen σ vT cm3 y en ese volumen debe encontrarse un único planeta. Pero l/n también representa el volumen que contiene un único planeta. Por tanto, las dos cantidades son iguales y
T = (n σ v)-1;
T se llama tiempo libre medio.
En realidad, el cometa se desplaza según una órbita elíptica y el tiempo necesario para colisionar estará influido en cierto modo por las fuerzas gravitatorias. Sin embargo, es fácil demostrar (véase, por ejemplo, Urey, 1951) que para valores típicos de v y excursiones relativamente breves de la historia del sistema solar, como las que considera Velikovsky, los efectos gravitatorios aumentan la sección eficaz de colisión σ en una pequeña proporción, de forma que, utilizando la ecuación anterior, obtendremos resultados muy próximos a los correctos.
Los objetos que desde las primeras épocas del sistema solar han producido cráteres de impacto en la Luna, la Tierra y los planetas interiores tienen órbitas muy excéntricas: los cometas y, especialmente, los objetos Apollo, que son asteroides o cometas muertos. Mediante ecuaciones sencillas del tiempo libre medio, los astrónomos son capaces de determinar con gran precisión, por ejemplo, el número de cráteres sobre la Luna, Mercurio o Marte, producidos desde la formación de dichos objetos: son los resultados de colisiones fortuitas de un objeto Apollo o, más raramente, de un cometa con la superficie lunar o planetaria. De la misma manera, la ecuación permite predecir correctamente la edad de los cráteres de impacto más recientes sobre la Tierra, como el Meteor Crater en Arizona. Estas concordancias cuantitativas entre la observación y la física de las colisiones proporcionan una buena garantía de que resulta adecuado aplicar estas mismas consideraciones al problema que consideramos.
Ya estamos en condiciones de hacer algunos cálculos relacionados con la hipótesis fundamental de Velikovsky. En la actualidad no hay objetos Apollo de diámetros superiores a algunas decenas de kilómetros. Los tamaños de los objetos del cinturón de asteroides, o de cualquier otro lugar en el que las colisiones determinan los tamaños, pueden conocerse gracias a la física de los choques. El número de objetos en un intervalo de tamaños es proporcional al radio del objeto elevado a una potencia negativa, normalmente comprendida entre 2 y 4. Así pues, si el cometa protoVenus de Velikovsky hubiese sido miembro de alguna familia de objetos del tipo Apollo o cometas, la probabilidades de encontrar un cometa velikovskiano de 6000 km de radio sería mucho menor que una millonésima de la probabilidad de encontrar alguno de 10 km de radio. Un número más verosímil sería mil millones de veces menos probable, pero ofrezcamos el beneficio de la duda a Velikovsky.
Como hay unos diez objetos Apollo de radios superiores a unos 10 km, la probabilidad de que exista un cometa velikovskiano es, por tanto, menor que 100 000 a 1 contra la proposición. La abundancia en estado estable de un objeto de esas características sería (con r = 4 u.a. e i = 1,2°) n = (10 × 10-5)/4 × 1040 = 2,5 × 10-45 cometas velikovskianos/cm3. El tiempo libre medio para chocar con la Tierra sería entonces T = 1/(n σ v) = l/[(2,5 × 10-45 cm-3) × (5 × 1018 cm2) × (2 × 106 cm s-1] = 4 × 1021 segundos ≅ 1014 años, lo cual es mucho mayor que la edad del sistema solar (5 × 109 años). Es decir, si el cometa de Velikovsky formase parte de la población de otros restos de colisiones en el sistema solar interior, resultaría un objeto tan raro que, en principio, nunca chocaría con la Tierra.
Pero en lugar de dejarlo aquí vamos a proseguir con la hipótesis de Velikovsky y nos preguntaremos cuánto tiempo necesita ese cometa, desde su eyección del interior de Júpiter, para colisionar con un planeta en el sistema solar interior. Entonces, n es ahora la abundancia [(10-40 cm-3) × (5 × 1018 cm2) × (2 × 106 cm s-1)] = 1015 segundos ≅ 3 × 107 años. Por tanto, la probabilidad de que un «cometa» de Velikovsky colisione o roce la Tierra en los últimos miles de años es (3 × 104)/(3 × 107) = 10-3, es decir, una probabilidad de 1 por 1000 —si es independiente de las demás poblaciones de restos. Si forma parte de dichas poblaciones, la situación empeora hasta (3 × 104)/1014 = 3 × 10-10, es decir, una probabilidad de 1 en 30 000 millones.
Una formulación más exacta de la teoría de colisiones orbitales puede encontrarse en un trabajo clásico de Ernst Öpik (1951). Considera un cuerpo blanco de masa m0 y de elementos orbitales a0, e0 = i0 = 0 en órbita alrededor de un cuerpo central de masa M. Entonces, un cuerpo de prueba de masa m y elementos orbitales a, e, i y un período P tiene un tiempo característico T antes de aproximarse a una distancia menor que R del cuerpo blanco, siendo
siendo U la velocidad relativa «en el infinito» y Ux, su componente sobre la línea de los nodos.
Si R es el radio físico del planeta, entonces,
Venus La Tierra Marte Jupiter Q × 105 5,6 4,3 1,5 8,8 2m0/MQ 0,088 0,14 0,043 21,6
Aplicando los resultados de Öpik al problema que estamos considerando, las ecuaciones se reducen a la siguiente aproximación:
Haciendo P ≅ 5 años (a ≅ 3 u.a.), tenemos
T ≅ 9 × 109 sen i años,
o aproximadamente 1⁄3 del tiempo para el recorrido libre medio obtenido mediante los sencillos argumentos mencionados más arriba.
Cabe destacar que en ambos cálculos, una aproximación a menos de N radios terrestres tiene N2 veces la probabilidad de una colisión física. Así, para N = 10, una aproximación a 63 000 km, los valores anteriores de T han de reducirse en dos órdenes de magnitud. Se trata de 1⁄6 de la distancia entre la Tierra y la Luna.
Para reproducir un escenario velikovskiano, se requiere una aproximación mayor: en definitiva, el libro se titula Worlds in Collision. En él también se dice que, como resultado del acercamiento de Venus a la Tierra, los océanos se elevaron hasta más de 2500 km. A partir de ahí, yendo hacia atrás, se pueden hacer unos cálculos sencillos utilizando la teoría de las mareas (la altura de la marea es proporcional a M/r3, siendo M la masa de Venus y r la distancia entre los planetas durante el encuentro) y se deduce que Velikovsky se está refiriendo a colisión de tipo roce: las superficies de la Tierra y Venus se tocaron levemente. Pero conviene señalar que ni siquiera una aproximación de 63 000 km es capaz de hacer compaginar la hipótesis con la física de las colisiones, como se ha visto en este apéndice.
Por último, mencionar que una órbita que corte las de Júpiter y la Tierra presenta una probabilidad elevada de volver a acercarse a Júpiter, el cual expulsaría el objeto fuera del Sistema Solar antes de que pudiese aproximarse a la Tierra —un ejemplo lo constituye la trayectoria del vehículo espacial Pioneer 10. Así pues, la existencia actual del planeta Venus debe suponer que el cometa velikovskiano pasó en repetidas ocasiones cerca de Júpiter y que, por tanto, su órbita se circularizó rápidamente. (En el texto se discute el hecho de que no parece existir ninguna forma de alcanzar esa circularización tan rápida). Por eso, Velikovsky debe suponer que el acercamiento del cometa a la Tierra se produjo poco después de que éste fuese expulsado por Júpiter —lo cual concuerda con los cálculos anteriores.
Entonces, la probabilidad de que el cometa alcanzase la Tierra sólo unas decenas de años después de ser expulsado por Júpiter está comprendida entre uno en un millón y uno en tres billones, en los dos casos de pertenencia a poblaciones existentes de restos. Aun cuando supusiéramos que el cometa fue expulsado de Júpiter, como sostiene Velikovsky, y diésemos como buena la poco probable hipótesis de que no estaba relacionado con ninguno de los demás objetos que podemos observar actualmente en el Sistema Solar —es decir, de que los objetos menores nunca son expulsados desde Júpiter—, el tiempo medio para que chocase con la Tierra sería de unos 30 millones de años, lo cual no concuerda con su hipótesis en un factor de 1 millón aproximadamente. Aun dejando que su cometa vagase por el sistema solar interior durante siglos antes de aproximarse a la Tierra, la estadística sigue manifestándose fuertemente adversa a la hipótesis de Velikovsky. Cuando se incluye el hecho de que Velikovsky cree en varias colisiones estadísticamente independientes en unos pocos centenares de años (véase el texto), la probabilidad de que su hipótesis sea cierta se vuelve prácticamente nula. Sus repetidos encuentros planetarios requerirían lo que podría llamarse Worlds in Collusion (Mundos confabulados).