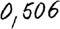
La Praça do Comércio se desperezaba con la modorra apacible de la mañana. El sol hacía resplandecer las fachadas blancas y las barandillas metálicas de los viejos edificios que rodeaban la plaza, donde sólo sobresalía el amarillo tostado del frontispicio casi rústico de la vieja iglesia románica de São Tiago. Pequeños puestos de venta animaban la plaza, exhibiendo ropas alegres, porcelana azul de la región y bisutería común. La terraza era instigadora, así que padre e hijo se instalaron en una mesa, extendieron las piernas y volvieron la cara hacia el astro flameante, acogiendo con placer el agradable calor que les entibiaba la piel.
Apareció el camarero con un bloc de notas en la mano y, frente a su mirada inquisitiva, los clientes les pidieron dos cafés expresos. Cuando el joven se alejó, Tomás miró lánguidamente a su padre.
—Usted me dijo hace un momento que la indeterminabilidad no pertenecía solamente al mundo cuántico…
—Sí.
—Pero, o bien me equivoco, o bien eso contradice todo lo que se dijo antes. ¿No es que eran deterministas la teoría de la relatividad y la física clásica de Newton?
—Lo eran y lo son.
—Y ambas establecen que el comportamiento de la materia es previsible…
—No exactamente.
—No entiendo. Según me dijeron el otro día, si yo sé la posición, la velocidad y la dirección de la Luna, podré calcular con exactitud todos sus movimientos pasados y futuros. ¿No es eso previsibilidad?
—Las cosas no se dan exactamente así. Ha habido descubrimientos posteriores que lo han cambiado todo.
—¿Qué descubrimientos?
Apareció el camarero y sirvió los dos cafés en la mesa. Manuel Noronha se enderezó en la silla, bebió un trago tímido y recorrió el cielo con los ojos, observando los copos de algodón que se deslizaban suavemente sobre el azul límpido.
—Dime una cosa, Tomás. ¿Por qué razón no logramos prever con rigor el estado del tiempo?
—¿Eh?
El matemático señaló el cielo.
—¿Por qué razón el boletín meteorológico en la televisión preveía para hoy cielo despejado sobre Coimbra y yo estoy viendo pasar unas nubes que desmienten la previsión?
—Qué sé yo —se rio Tomás—. Porque nuestros meteorólogos son unos nabos, supongo.
El padre volvió a estirarse en su lugar, con el rostro vuelto hacia el calor del sol.
—Respuesta equivocada —dijo—. El problema está en la ecuación.
—¿Cómo?
—En 1961, un meteorólogo llamado Edward Lorenz se sentó ante un ordenador y se puso a ensayar previsiones meteorológicas sobre el comportamiento del clima a largo plazo, basándose en sólo tres variaciones: la temperatura, la presión del aire y la velocidad del viento. La experiencia nada revelaría de especial si no se hubiese dado el caso de que quiso examinar una secuencia determinada con más detalle. Fue algo pequeño, casi insignificante. En vez de introducir cierto dato otra vez desde el principio, fue a ver una copia impresa de la experiencia original y copió el número que vio allí. —Sacó un bolígrafo del bolsillo de la chaqueta y cogió una servilleta de papel, que extendió sobre la mesa de la terraza—. Era, si mal no recuerdo, el…, eh…
Escribió cuatro cifras.
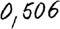
—Era 0,506.
—Vaya, eso sí que es tener buena memoria —comentó el hijo.
—Nosotros, los matemáticos, somos así. —Sonrió y señaló las tazas humeantes sobre la mesa—. Ahora bien: tal como estamos haciendo ahora, Lorenz fue a tomar un café y dejó el ordenador procesando los datos. Cuando regresó, no obstante, no quería creer en lo que lo esperaba. Descubrió que la nueva previsión meteorológica que daba el ordenador era totalmente diferente de la anterior. Totalmente. Intrigado, intentó ver lo que había cambiado. —Golpeó con la punta del bolígrafo los cuatro dígitos que había garrapateado en la servilleta de papel—. Después de analizarlo todo, se dio cuenta de que, al introducir este dato, sólo había reproducido cuatro guarismos de una secuencia más larga.
Escribió la secuencia completa.
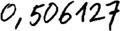
—Ésta era la secuencia completa original. Enfrentado a esta situación, tomó conciencia de que una alteración millonésima de los datos, una cosa infinitamente pequeña, casi insignificante, alteraba por completo la previsión. Era como si una mera ráfaga de viento imprevista tuviese el poder de cambiar el estado del tiempo en todo el planeta. —Hizo una pausa dramática—. Lorenz descubrió el caos.
—¿Perdón?
—La teoría del caos constituye uno de los modelos matemáticos más fascinantes que existen, y ayuda a explicar muchos comportamientos del universo. La idea fundamental de los sistemas caóticos es simple de formular. Pequeñas alteraciones en las condiciones iniciales provocan profundas alteraciones en el resultado final. O sea, pequeñas causas, grandes efectos.
—Deme un ejemplo.
El padre volvió a apuntar al cielo y a las nubes intermitentes que, a veces, lanzaban irritantes sombras sobre la Praça do Comércio.
—El estado del tiempo —dijo—. El ejemplo más famoso es el llamado «Efecto Mariposa». El batir de las alas de una mariposa en Coimbra alterará en una porción millonésima la presión del aire a su alrededor. Esa pequeñísima alteración producirá un efecto dominó en las moléculas de aire, hasta el extremo de provocar, dentro de un tiempo, una tormenta colosal en América. Y ése es el Efecto Mariposa. Ahora, transporta el efecto de esta pequeña mariposa al efecto de todas las mariposas en el mundo, de todos los animales, de todo lo que se mueve y respira. ¿Cuál es el resultado? —Abrió las manos, como quien expone una evidencia—. La imprevisibilidad.
—Que remite al indeterminismo.
—No —exclamó el matemático—. La imprevisibilidad no remite al indeterminismo, sino a la indeterminabilidad. El comportamiento de la materia sigue siendo determinista. Lo que ocurre es que la materia se organiza de tal modo que no es posible prever a largo plazo su comportamiento, aunque éste ya esté determinado. Si quieres, podremos decir que el comportamiento de los sistemas caóticos es causal, pero parece casual.
—Ya… —murmuró Tomás—. ¿Cree que, siendo eso válido para la meteorología, puede aplicarse también en otros campos?
—Tomás, la teoría del caos está presente por todas partes. En todo. En el mundo cuántico, tal vez, no logramos prever con toda certidumbre el comportamiento de las micropartículas por la simple razón de que es caótico. Ese comportamiento ya está determinado, pero las fluctuaciones en sus condiciones iniciales son de tal modo minúsculas que no nos resulta posible anticipar su evolución. Por ello, a efectos prácticos, el mundo cuántico nos parece indeterminista. En realidad, las micropartículas tienen un comportamiento determinista, pero el hecho es que no llegamos a determinarlo. Creo que eso se debe a la influencia de la observación, según lo establecido inicialmente por el principio de incertidumbre, pero también a la indeterminabilidad inherente a los sistemas caóticos.
—Está bien, pero eso sólo ocurre con cosas minúsculas, como los átomos o las moléculas…
—Te equivocas —insistió el padre—. El caos está en todas partes, incluidos los grandes objetos. El propio sistema solar, que parece tener un comportamiento previsible, es, en realidad, un sistema caótico. Lo que ocurre es que no nos damos cuenta de ello porque observamos movimientos muy lentos. Pero el sistema solar es caótico. Una proyección hecha desde un ordenador calculó, por ejemplo, que si la Tierra empezase a girar alrededor del Sol a sólo cien metros de distancia del local donde efectivamente comenzó, al cabo de cien millones de años se alejaría cuarenta millones de kilómetros de la ruta original. Pequeñas causas, grandes efectos.
—Hmm.
—El caos rige incluso nuestras vidas. Imagina, por ejemplo, que te metes en el coche y, antes de arrancar, te das cuenta de que la solapa de tu chaqueta ha quedado enganchada a la puerta. ¿Qué haces entonces? Abres la puerta, te acomodas la solapa, cierras la puerta y arrancas. Has perdido cinco segundos en ese proceso. Cuando llegues a la primera esquina, aparece un camión que te atropella. Resultado: te quedas parapléjico para el resto de tu vida. Ahora imagina que no se te ha enganchado la solapa de la chaqueta en la puerta. ¿Qué ocurre? Arrancas inmediatamente y llegas a la esquina cinco segundos antes, ¿no? Miras a la derecha, ves el camión que se acerca, esperas a que pase y después prosigues tu viaje. Ésta es la teoría del caos. A causa de la solapa de la chaqueta enganchada en la puerta del coche, has perdido cinco segundos que marcarán la diferencia durante lo que te queda de vida. —Hizo un gesto resignado—. Pequeñas causas, grandes efectos.
—¿Todo a causa de una cosa tan pequeña?
—Sí. Pero atención: ya estaba determinado que se te engancharía la solapa de la chaqueta en la puerta del coche. Ocurrió que te pusiste mal la chaqueta por la mañana. Y te la pusiste mal porque te despertaste de mal humor. Y te despertaste de mal humor porque dormiste poco. Y dormiste poco porque te acostaste tarde. Y te acostaste tarde porque tenías un trabajo que hacer para la facultad. Y tenías que hacer ese trabajo por el motivo que sea. Todo es causa de todo y provoca consecuencias que se vuelven causas de otras consecuencias, en un eterno efecto dominó, en que todo está determinado pero permanece indeterminable. El propio conductor del camión podría haber frenado a tiempo, pero no lo hizo porque vio a una mujer guapa pasando y giró la cabeza para mirarla. Y la mujer pasó por allí en ese momento porque andaba con retraso. Y se retrasó porque su novio la llamó por teléfono. Y el novio la llamó por el motivo que sea. Todo es causa y consecuencia.
Tomás se pasó la mano por el pelo, intentando ordenar las ideas.
—Un momento —dijo—. Vamos a imaginar que es posible archivar todos los datos del universo en un superordenador. En ese caso, ¿podríamos prever todo el pasado y todo el futuro?
—Sí, se aplicaría el Demonio de Laplace. Todo el pasado y el futuro ya existen, y si supiésemos todas las leyes y lográsemos definir con precisión, y simultáneamente, la velocidad, dirección y posición de toda la materia, lograríamos ver todo el pasado y el futuro.
—Por tanto, en teoría eso es posible…
—No, en teoría no es posible.
—Disculpe —rectificó Tomás—. En teoría es posible. No lo es en la práctica.
El padre meneó la cabeza.
—Ésa es una sutileza más del universo —dijo—. Si lográsemos saber todo sobre el estado presente del universo, lograríamos determinar el pasado y el futuro, dado que ya está todo determinado. Pero incluso desde el punto de vista teórico no es posible saber todo sobre el estado presente del universo.
—¿Ah, sí? ¿Y por qué no?
—Por otra sutileza inherente al universo —respondió el matemático—. El infinito.
Tomás esbozó una mueca.
—¿El infinito?
—Sí. ¿Nunca has oído hablar de la paradoja de Zenón?
—Pues… sí.
—Descríbela, por favor.
—¿Qué es esto? ¿Un examen?
—¡Anda ya! ¡Vamos, descríbela!
El hijo entrecerró los ojos e hizo un esfuerzo de memoria.
—Bien…, eh…, si no recuerdo mal, es aquella historia de la carrera que disputan una tortuga y una liebre, ¿no? La tortuga sale primero, pero la liebre, que es mucho más rápida, pronto la supera. El problema es que, según Zenón, la liebre nunca podría alcanzar a la tortuga porque el espacio que las separa es infinitamente divisible. Es así, ¿no?
—Sí —confirmó el padre—. La paradoja de Zenón ilustra el problema matemático del infinito. Para correr un metro, la liebre tiene que correr la mitad de esa distancia. Y esa mitad también es divisible por otra mitad, y la otra mitad por otra mitad, y así hasta el infinito.
—Pero ¿qué quiere probar, padre, con eso?
—Lo que quiero probar es que el infinito es un problema insuperable para la cuestión de la previsibilidad. —Hizo una vez más un gesto en dirección al cielo—. Volvamos al ejemplo del estado del tiempo. Hay dos órdenes de factores que imposibilitan la previsión a largo plazo. Uno es eminentemente práctico. Aunque yo sepa cuáles son todos los factores que influyen en el estado del tiempo, tendría que considerarlos todos. La respiración de cada animal, el movimiento de cualquier ser vivo, la actividad solar, una erupción volcánica, el humo que despide cada automóvil, cada chimenea, cada fábrica, todo. En conclusión: tengo una imposibilidad práctica de tomar en cuenta todos estos factores de manera simultánea, ¿no?
—Claro, eso no es posible.
—Pero el segundo orden de factores está relacionado con el problema del infinito. Por ejemplo, vamos a imaginar que tenga que medir la temperatura global en un momento dado para poder hacer extrapolaciones. Supongamos que, aquí en Coimbra, pongo el termómetro y lo mido a mediodía…, eh…, no sé, dame un valor.
—¿Veinte grados?
El padre volvió a sacar el bolígrafo de la chaqueta y apuntó unos números en la misma servilleta de papel donde ya había garrapateado el valor que había llevado a Lorenz a descubrir los sistemas caóticos.
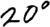
—Muy bien, 20 grados —dijo el matemático—. Pero la verdad es que esta medición está incompleta, ¿no? Sólo he medido las unidades. Pero sabemos que las pequeñas alteraciones en las condiciones iniciales conducen a grandes alteraciones en las condiciones finales. Si es así, es imprescindible saber cuál es la medición decimal, centesimal y milesimal, ¿no?
—Bien, entonces añádala.
Manuel agregó tres guarismos.
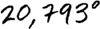
—Pero… ¿y los valores siguientes? ¿No podrán ser también importantes? La teoría del caos dice que sí. Por tanto, tenemos que poner los valores siguientes, por muy minúsculos que sean, dado que cualquier pequeña alteración puede producir efectos gigantescos.
—Hmm.
El matemático añadió más guarismos.
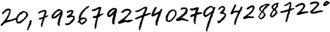
—Pero incluso esto no alcanza —afirmó—: el guarismo que siga a todos éstos también puede ser crucial —sonrió—. Lo que quiero decir es que la medición tendría que llevar un número infinito de guarismos. Pero eso no es posible, ¿no? Por tanto, por más guarismos que pongamos, nunca podremos saber con exactitud la temperatura en un determinado lugar y hora, puesto que tendríamos que hacer una cuenta que abarcase datos infinitesimales.
—Ah, ya lo he entendido.
—Pero el problema es aún más complejo que esto —golpeó la mesa—: la temperatura que tenemos en esta mesa puede ser ligeramente diferente de la temperatura que existe allí, a sólo un metro de distancia. —Señaló hacia un lado—. En consecuencia, tendríamos que medir todos los espacios de Coimbra. Pero eso no es posible, ¿no? Tal como en la paradoja de Zenón, es fácil comprobar que cada metro es infinitamente divisible. Yo tendría que medir la temperatura en todos los espacios existentes para poder saber cuáles son las condiciones iniciales. Pero como la distancia entre cada espacio, por más pequeña que sea, es siempre divisible por la mitad, nunca lograría medir todo el espacio. Y lo mismo se aplica al tiempo. La diferencia entre un segundo y otro es infinitamente divisible, ¿no? Ahora bien: entre un instante y otro puede haber sutiles variaciones de temperatura que exigen ser medidas. Pero como la división entre el tiempo es igualmente infinita, según el principio que enuncia la paradoja de Zenón, nunca lograré obtener esa medición. Recuerda que el razonamiento implícito en la paradoja de Zenón nos indica que existe tanto espacio en un metro como en el universo entero, existe tanto tiempo en un segundo como en toda la eternidad, y ésta es una propiedad misteriosa del universo.
—Lo veo…
Manuel cogió la taza y sorbió todo el café que quedaba. Respiró hondo, se distendió en la silla y cerró los ojos, disfrutando del placentero calor que irradiaba el sol.
—¿Te acuerdas de que el otro día te hablé de los teoremas de la incompletitud, de Gödel?
—Sí.
—Vamos a ver si te acuerdas de qué iban —dijo—. ¿En qué consisten esos teoremas?
Tomas sacudió la cabeza, con enfado.
—¡Oiga, padre! Y qué sé yo…
El padre abrió un ojo y miró a Tomás.
—¿No los recuerdas?
—¡No!
—Así, pues, ¿no te acuerdas de que dije que los teoremas de la incompletitud muestran que un sistema matemático no consigue probar todas sus afirmaciones?
—Ah, sí.
—Esa demostración fue de gran importancia, ¿entiendes?
—Pero ¿por qué? ¿Qué tiene eso de extraordinario?
—Es muy sencillo —dijo Manuel—. Los teoremas de la incompletitud desvelaron una nueva característica misteriosa del universo. A través de esos dos teoremas, lo que el universo nos dice es lo siguiente: hay ciertas cosas que vosotros, los seres humanos, sabéis que son verdaderas, pero jamás podréis probarlo, a causa de la forma majestuosa en que yo, el universo, he ocultado el último resto de la verdad. Podréis conocer gran parte de la verdad, pero las cosas están concebidas de modo tal que jamás conseguiréis aprehenderla íntegramente. ¿Entiendes ahora?
—Sí.
El matemático abrió las manos, con su gesto característico, el que empleaba siempre que daba por probados sus argumentos.
—Voilà! —exclamó—. El principio de incertidumbre, los sistemas caóticos y los teoremas de la incompletitud tienen un significado profundo al revelarnos las sutilezas increíbles del funcionamiento del universo. —Abarcó el cielo con un gesto—. Todo el cosmos se asienta en la matemática. Las leyes fundamentales del universo se expresan en ecuaciones y fórmulas matemáticas, las leyes de la física son algoritmos para el procesamiento de información y el secreto del universo se encuentra codificado en lenguaje matemático. Todo está ligado con todo, hasta lo que no parece tener ligación. Pero ni siquiera el lenguaje matemático logra decodificar totalmente ese código. Ésa es la propiedad más enigmática del universo: la forma en que él oculta la verdad final. Todo está determinado, pero todo es indeterminable. La matemática es el lenguaje del universo, pero no tenemos manera de probarlo más allá de cualquier duda. Cuando vamos al fondo de las cosas, siempre encontramos un extraño velo que oculta las últimas facetas del enigma. El creador esconde allí su firma. Las cosas están concebidas con tal sutileza que no es posible desvelar por completo su secreto más profundo.
—Hmm.
—Siempre habrá misterio en el fondo del universo.