Inflación

Propuesta en 1981, la teoría de la inflación de Alan Guth ofrecía una explicación al hecho de que las condiciones iniciales en el big bang fueran aproximadamente —aunque no exactamente— uniformes.

En el universo observamos hoy cuatro fuerzas fundamentales: las fuerzas nucleares fuerte y débil, el electromagnetismo y la gravedad. Todas ellas poseen intensidades distintas, la más débil de las cuales es la gravedad. En los inicios del universo, sin embargo, esas fuerzas pudieron haber tenido la misma intensidad y haber hecho realidad una única fuerza que quizá podría explicar algún día una hipotética teoría del todo. Así pues, en el universo primitivo, las leyes físicas habrían sido diferentes. Por ello, la constante cosmológica —la densidad de energía del vacío— también podría haber sido distinta en la fase inicial. Einstein no consideró esta posibilidad. Guth propuso que, en el universo inicial, la densidad de energía del vacío fue gigantesca y constituyó la forma de energía dominante; la geometría resultante estaría de acuerdo con la relatividad general. ¿Qué aspecto tendría esa geometría? Hoy conocemos ya la respuesta.

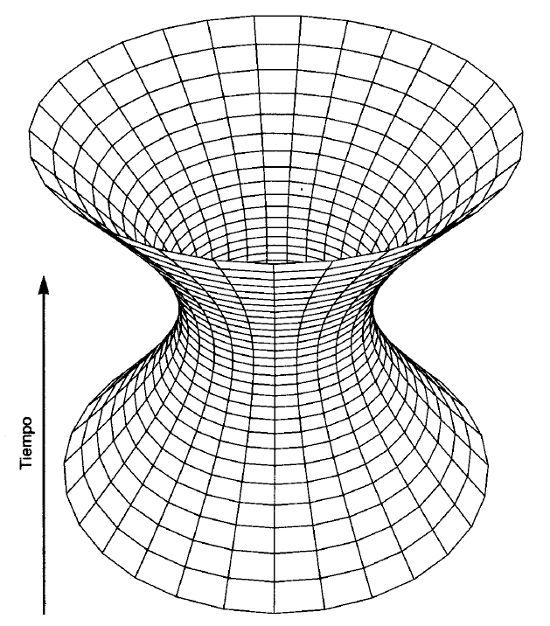
Cuando Einstein tuvo la idea de la constante cosmológica en 1917, añadió materia ordinaria para producir una cosmología estática. Pero, meses después, aquel mismo año, el astrónomo holandés Willem de Sitter se preguntó qué sucedería si un universo tuviera una constante cosmológica y nada más. El resultado se conoce como espacio-tiempo De Sitter y está ilustrado en la figura 21. Para comprender la inflación, antes debemos entender el espacio-tiempo De Sitter, el cual recuerda la superficie de un reloj de arena infinito, con un cono abierto hacia el pasado y otro cono abierto hacia el futuro, unidos por una estrecha cintura. Como en los diagramas anteriores, la ilustración sólo muestra una dimensión espacial, arrollada horizontalmente, más la dimensión tiempo, en dirección vertical. Se trata de un universo triesférico cenado que arranca en el infinito pasado con un tamaño infinito y se contrae a una velocidad cercana a la de la luz. El efecto de repulsión de la constante cosmológica hace que esa contracción se frene y llegue a invertir su sentido. El universo alcanza un tamaño mínimo y luego empieza a expandirse, al principio muy despacio y después cada vez más deprisa, hasta acabar acercándose a la velocidad de la luz. Si cortamos el modelo de la figura 21 con un plano horizontal, la sección mostrará un círculo que representa la circunferencia del universo triesférico en ese momento. Moviendo el plano de abajo arriba veríamos cómo la sección circular se va encogiendo hasta alcanzar un mínimo en la cintura, sobrepasado el cual comienza a crecer.

FIGURA 21. Espacio-tiempo De Sitter.

Si hubiera partículas en ese universo, sus líneas de universo serían como las curvas verticales del diagrama. Las líneas se aproximarían una a otra al principio, llegando a su mínima separación en la cintura, y después comenzarían a separarse como las «ballenas» de un corsé. A medida que la velocidad de las partículas se incrementa, acercándose a la de la luz, el espacio-tiempo De Sitter se va pareciendo más a un cono abierto hacia arriba con un ángulo de 45 grados. Cuando esto sucede, los relojes de las partículas marchan cada vez más despacio, según la relatividad especial. Conforme se enlentece el tictac de esos relojes, el universo se va expandiendo más en cada intervalo. De hecho, las partículas «ven» crecer exponencialmente la circunferencia del universo (2, 4, 8, 16, 32, 64, y así sucesivamente) en función del tiempo medido por sus relojes.

Guth llamó «inflación» a esta fase de expansión del universo debido a que el tamaño de éste se duplica en cada intervalo (como los precios en un periodo de alta inflación monetaria). La distancia entre dos partículas, estimada a partir de sus relojes cada vez más lentos, crecería también exponencialmente. Al final, esas partículas «pensarían» que se estaban alejando una de otra a una velocidad mayor que la de la luz. Pero ello no constituye paradoja alguna.^[39] La relatividad especial se limita a establecer que dos objetos no pueden cruzarse a una velocidad mayor que la de la luz, Nada impide que el espacio entre dos objetos se expanda tan deprisa que un rayo de luz no pueda cruzar la creciente distancia que los separa.

Como el espacio-tiempo De Sitter representa un universo que se contrae hasta un estado cercano a un big crunch para luego rebotar y comenzar a expandirse, parece hecho a medida para el modelo de Universo oscilante. Cuando un universo colapsa en dirección a un big crunch, se va haciendo más caliente y más denso a medida que la materia se comprime. De forma simultánea, la circunferencia de ese universo disminuye con el tiempo, como la parte superior del balón de rugby en la figura 19. En última instancia, el universo alcanza una temperatura tal que se produce un cambio en el estado cuántico del vacío, por lo que se origina una constante cosmológica grande. Los efectos de repulsión debidos a esa constante frenan entonces el proceso de contracción y logran invertir su sentido. El universo alcanzaría un tamaño mínimo en la cintura del espacio-tiempo De Sitter y comenzaría luego a expandirse.

Para visualizar el modelo, tomaríamos un ciclo del Universo oscilante y eliminaríamos el extremo superior, correspondiente al big crunch, como si cortáramos la punta de un habano. Luego pondríamos una pequeña pieza en forma de reloj de arena —un pequeño espacio-tiempo De Sitter— en su lugar. Cortaríamos entonces el extremo inferior del ciclo siguiente —el que corresponde al big bang— y colocaríamos el resto del balón sobre la pieza de empalme. Habríamos eliminado así las singularidades del big bang y el big crunch y conectado la fase de colapso de un ciclo con la de expansión del siguiente mediante un espacio-tiempo De Sitter. En este escenario, la circunferencia de la cintura espaciotemporal puede ser muy pequeña: entre 10^-33 y 10^-26 centímetros. Un tamaño semejante a un punto, casi una singularidad. A un observador situado en la fase expansiva posterior, este universo le parecería exactamente igual que el modelo del big bang.

Según Guth, una fase De Sitter resuelve la cuestión de cómo se inició la expansión del universo: la provocaron los efectos de repulsión gravitatoria debidos a la constante cosmológica inicial. Con el tiempo, el vacío inflacionario de alta densidad se transformaría en radiación térmica normal de alta temperatura y la expansión continuaría como en el modelo del big bang. Y con la radiación y la materia normales como único contenido, esa expansión se enlentecería con el tiempo, también como en dicho modelo.

Guth también explicaba de esta forma por qué el big bang habría sido tan uniforme. Las regiones que hubieran tenido tiempo de intercambiar señales lumínicas se habrían equilibrado a una misma temperatura. Luego, a medida que el universo se inflara, duplicando continuamente su tamaño, esas regiones dejarían de tener relación causal al ser incapaces de intercambiar señales de ese tipo. Pero tras la degradación del vacío inflacionario, la expansión aminoraría su marcha y las regiones volverían a hallarse en contacto. Como expresaba gráficamente el astrofísico Bill Press, «se dirían hola, adiós y, después, hola de nuevo». Cuando las regiones que habían alcanzado la misma temperatura antes de perder contacto se saludaran otra vez, se encontrarían también en equilibrio térmico. Al observar el fondo de microondas en distintas direcciones, vemos que toda la materia está aproximadamente a la misma temperatura. Esas regiones estaban al principio lo suficientemente cerca unas de otras como para haber intercambiado fotones en la fase De Sitter del universo primitivo. Esta clase de equilibrio no sería posible en el modelo estándar del big bang, en el que las regiones que vemos hoy se habrían estado «diciendo hola» unas a otras desde el origen de los tiempos. Si, en cambio, nuestro universo hubiera surgido de un estado de vacío de alta densidad y no de una singularidad como el big bang, el hecho podría explicar por qué el fondo de microondas tiene ese alto grado de uniformidad que observamos.

Pero esa uniformidad no es total. Las regiones inicialmente en contacto causal eran tan pequeñas que, según el principio de incertidumbre, tuvieron que existir fluctuaciones apreciables en la densidad de energía entre un lugar y otro. Tal como han apuntado James Bardeen, de la Universidad de Washington, y sus colegas Paul Steinhardt y Michael Tumer, esas fluctuaciones se habrían suspendido por no existir contacto causal entre las regiones, que tendrían más o menos la misma magnitud (1 parte en 100.000, aproximadamente) cuando «se dijeran hola» otra vez. Pero dichas regiones habrían crecido enormemente mientras se hallaban fuera de contacto y el universo duplicaba una y otra vez su tamaño.

Según el modelo inflacionario, una región que tuviera inicialmente un tamaño igual o menor de 10^-26 centímetros podría crecer hasta una extensión de miles de millones de años luz. Podemos calcular cómo evolucionarían las fluctuaciones en un universo inflacionario y comparar los resultados con nuestras observaciones del fondo de microondas. El hecho es que ambos aspectos coinciden.

Un punto importante es que las fluctuaciones cuánticas en la densidad predichas por la inflación deberían ser aleatorias. En consecuencia, las geometrías tridimensionales de las regiones de alta y baja densidad que se formaran en el universo deberían ser equivalentes. Esto es posible en una geometría espongiforme, según indicábamos Adrian Melott, Mark Dickinson y yo en 1986; una idea desarrollada después por Andrew Hamilton, David Weinberg, Changbom Park, Michael Vogeley, Trinh Thuan, Wes Colley y yo mismo en compañía de otros colegas. Una esponja tiene interiores y exteriores que presentan formas similares. La mayoría de las muestras de galaxias registradas en la actualidad presentan distribuciones espongiformes. La muestra más grande, que abarca más de 15.000 galaxias, exhibe una gran coincidencia con la teoría. No deja de ser escalofriante que las estructuras que contemplamos hoy en el cosmos sean probablemente los restos fosilizados de las fluctuaciones cuánticas que tuvieron lugar en los primeros 10^-35 segundos de nuestro universo.

La inflación explica también por qué nuestro universo es tan grande: su tamaño se ha doblado una y otra vez. Una sucesión de esta clase (2, 4, 8, 16, 32, 64, etcétera) crece rápidamente: tras diez duplicaciones, el universo sería mil veces más grande; después de veinte, un millón; tras treinta duplicaciones, habría crecido mil millones de veces. El universo puede haber experimentado más de cien duplicaciones, incrementando su tamaño en un factor superior a 10³⁰, durante la fase inflacionaria.

Curiosamente, esa constante cosmológica que Einstein se sacó de la manga —la mayor pifia de su vida, según él— regresa ahora a modo de vacío inflacionario para ayudar a explicar el universo primitivo.

¡Una fase inflacionaria proporcionaría el rebote que convierte un big crunch en un big bang!^[40] Pero ¿y si pudiéramos comenzar simplemente desde la cintura estrecha del espacio-tiempo De Sitter, prescindiendo de la fase de contracción y de todos los universos anteriores? En la cintura, el universo inflacionario es muy pequeño; un universo cenado con un volumen diminuto, mucho más pequeño que el de un protón. Aun así, comienza a expandirse y da lugar finalmente al gigantesco universo que contemplamos hoy. A este respecto, Guth observó que se podría partir de cualquier minúsculo fragmento de estado de vacío inflacionario y, conforme se produce la expansión, obtener un volumen cada vez mayor de esa clase de vacío. No es posible partir de la nada, pero sí de algo realmente diminuto.^[41]

Si tomamos, pues, un pequeñísimo volumen de estado de vacío inflacionario, el fragmento crecerá indefinidamente. De hecho, ése era el único inconveniente que planteaba el artículo original de Guth. Como él mismo reconocía, encontrar una salida airosa para la inflación resultaba problemático. Por otra parte, como el estado de vacío inflacionario tenía densidad de energía positiva, era propenso en última instancia a degradarse, y se convertía en vacío normal, de densidad de energía más baja.

Según Guth, la inflación podría concluir cuando la energía del vacío inflacionario se hubiese transformado de golpe en radiación térmica en todo el espacio. Sería como poner la tetera llena de agua a calentar y encontrarse con que, de pronto, toda el agua se ha convertido en vapor. La distribución del vapor sería tan uniforme como el modelo del big bang caliente que observamos, pero se trata de un fenómeno muy improbable. Como todo el mundo sabe, cuando calentamos agua en un recipiente, el vapor forma burbujas. De hecho, Sidney Coleman, de Harvard, y su colega F. de Luccia apuntaron que un mar de vacío de alta densidad se degradaría probablemente debido a la formación de burbujas de vacío ordinario en su seno. Cada burbuja se expandiría tras su aparición y sus paredes avanzarían hacia el exterior a casi la velocidad de la luz. El estado de vacío en el interior de una burbuja es un vacío normal con densidad nula de energía y presión. Fuera de la burbuja, la presión sería negativa (una succión universal), por lo que el vacío inflacionario exterior tiraría simplemente de la pared de la burbuja hacia fuera, haciéndola expandirse. Sin embargo, las burbujas no llegarían nunca a percolar, llenando todo el espacio. Dos burbujas que hubieran surgido cerca chocarían al expandirse, pero las que brotaran lejos una de otra nunca podrían crecer lo suficientemente deprisa como para cubrir la distancia que las separa, dado que esa distancia aumenta a la misma velocidad. El resultado sería un mar de vacío de alta densidad en expansión permanente que contendría grupos de burbujas aislados. Se trataría de una distribución no uniforme, muy distinta del universo homogéneo que vemos. ¿Se malogró a causa de ello la extraordinaria y potente teoría de Guth? En absoluto. Guth era consciente del problema. La solución requería examinar esas burbujas con mayor detenimiento.