La cuestión de la causa primera

El dilema de la causa primera ha inquietado a filósofos y científicos desde hace dos mil años. Las causas preceden a los efectos. Si designamos una primera causa para el universo, un escéptico siempre podrá preguntar: «¿Y qué es lo que dio origen a eso? ¿Qué sucedió con anterioridad?». Para Aristóteles el universo existía eternamente, hacia el pasado y hacia el futuro, con lo que no había lugar a esas engorrosas preguntas. Ese modelo ha atraído también a muchos científicos modernos. Newton imaginaba un universo infinito en el espacio (en caso contrario, pensaba, colapsaría en una única masa) y eterno en el tiempo. Cuando Einstein desarrolló la relatividad general y la aplicó a la cosmología, su primer modelo cosmológico fue el universo estático de Einstein, el cual perduraba eternamente, sin principio ni final.

En el universo estático de Einstein, el volumen del espacio era finito, ya que éste se curvaba sobre sí mismo. Podemos tratar de entenderlo examinando una situación análoga: la superficie de la Tierra, que también se curva sobre sí misma. La superficie terrestre tiene un área finita, pero carece de borde alguno. Colón demostró que navegando siempre hacia el oeste, nunca llegábamos al «borde» de nuestro planeta, y Balboa demostró, por su parte, que manteniendo un mismo rumbo, lo rodeábamos y regresábamos al punto de partida.

La superficie de una esfera es un objeto bidimensional; para fijar una posición en ella bastan dos coordenadas: latitud y longitud. Imaginemos un planilandés que viviera en una superficie así. No le estaría permitido abandonar tal superficie, pero podría descubrir que el lugar donde reside es una esfera y no un piano al observar que, cuando viaja en línea recta, retorna al punto de partida. Si dispusiera de instrumentos de medida, constataría que la suma de los ángulos de un triángulo es mayor de 180 grados. En otras palabras, su mundo no obedecería las leyes de la geometría euclídea. El planilandés podría incluso construir un triángulo con los tres ángulos rectos trazando una línea recta desde el polo norte a un punto del ecuador, recorriendo un cuarto de vuelta a lo largo de éste y regresando finalmente a dicho polo. Nunca se podría trazar un triángulo así en una superficie plana, Nuestro planilandés descubriría, pues, que en lugar de Planilandia vive en Esferilandia (D. Burger utilizó este argumento en un relato con ese título). De manera similar, un linealandés unidimensional descubriría estar viviendo en Circulolandia en vez de en Linealandia si viajando siempre hacia la derecha observan que regresaba al punto de partida.

Un círculo es una versión unidimensional de una esfera. A veces, los matemáticos lo denominan uno-esfera. Una superficie esférica ordinaria, tal como la de una pompa de jabón, es llamada dos-esfera, ya que es bidimensional. En el universo estático de Einstein, la geometría del espacio es una tres-esfera, el equivalente tridimensional de la dos-esfera. Los habitantes de una tres-esfera viven en un espacio tridimensional que se curva sobre sí mismo. En el seno de un espacio de esta clase, si viajamos siempre hacia delante en una nave espacial, regresaremos finalmente al planeta del que hemos partido —llegando por la parte de atrás—, pues lo que creemos una línea recta es en realidad una circunferencia de longitud finita. Si salimos de la Tierra hacia la derecha, acabaremos retornando a ella por la izquierda, y si saliéramos hacia arriba, regresaríamos por abajo. No importa en qué dirección partamos, regresaremos al punto de partida tras haber recorrido una distancia igual a la longitud de la circunferencia de la tres-esfera. Esa tres-esfera podría ser muy grande y tener quizás una circunferencia de diez mil millones de años luz. Viajando a una velocidad menor que la de la luz, tardaríamos más de diez mil millones de años en rodeas el universo y volver a casa.

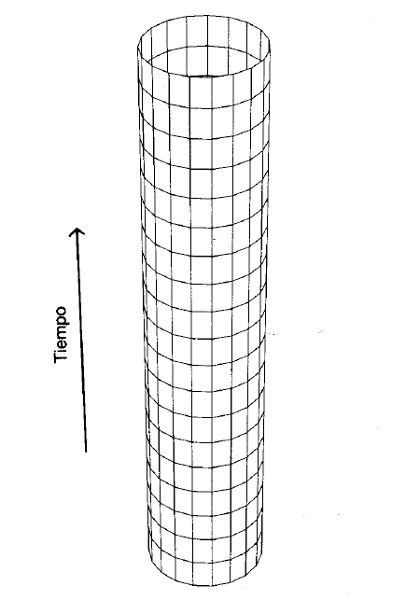
La figura 18 muestra un diagrama espaciotemporal del universo estático de Einstein. Presenta sólo una de las tres dimensiones espaciales más la dimensión temporal. El universo estático de Einstein se asemeja a la superficie de un cilindro, El tiempo fluye hacia arriba en dirección al futuro y la dimensión espacial representada rodea una circunferencia. Para saber qué aspecto tiene el universo en un momento dado basta con realizar un corte horizontal al cilindro: obtendremos un círculo. Ese círculo representa un círculo máximo de la tres-esfera. Para obtener una película de la evolución del universo a lo largo del tiempo iríamos desplazando ese corte hacia arriba. Veríamos que el tamaño del círculo permanece constante: el universo triesférico es estático; ni se expande ni se contrae, su circunferencia es siempre la misma. El cilindro se extiende indefinidamente hacia el pasado y hacia el futuro. Como pensaba Aristóteles, dicho universo nunca fue creó y jamás se destruirá, se limita a existir eternamente.

FIGURA 18. El universo estático de Einstein.

Pero a diferencia del universo de Newton, en el universo estático de Einstein el espacio se cierra sobre sí mismo y es finito. Sólo la superficie del cilindro es real. No existe nada fuera del cilindro ni tampoco en su interior. Las líneas de universo de las galaxias (y este universo tiene un número finito de ellas) son esas líneas rectas que van de abajo arriba a lo largo del cilindro. Las galaxias permanecen a distancia constante unas de otras. Si determinamos la distancia entre dos galaxias en un momento dado y repetimos la medición algún tiempo después, el resultado será idéntico en ambos casos. Obsérvese que ninguna galaxia en concreto ocupa una posición especial. Al igual que todos los puntos de la superficie de una esfera son equivalentes, los de una tres-esfera también lo son. No hay ninguna galaxia que pueda considerarse el centro.

Para crear este modelo, Einstein tuvo que alterar sus ecuaciones de la relatividad general. En su teoría, las estrellas se atraían unas a otras y, aunque se partiera de un universo en reposo, éste comenzaría a colapsar inmediatamente. Un modelo estático como el propuesto por Isaac Newton no era viable. Newton argumentaba que en un universo infinito, aunque las estrellas se atrajeran unas a otras, cada una de ellas tendría el mismo número de estrellas tirando en distintas direcciones, con lo que, en definitiva, se quedaría en su sitio (ni Newton ni Einstein conocían las galaxias, pero el razonamiento sería el mismo en cualquier caso). El argumento, cuestionado en la actualidad, resultaba aceptable en el marco de la teoría de Newton —dado que en ella existían los conceptos de espacio absoluto y tiempo absoluto—, pero no era aplicable en el caso de Einstein, Las ecuaciones einsteinianas mostraban claramente que un universo estático infinito que contuviera estrellas (y galaxias) existiendo eternamente, como proponía Newton, no era posible. De hecho, no era viable modelo estático alguno, Einstein tuvo que añadir un término nuevo a sus ecuaciones, que denominó constante cosmológica y que vendría a ser una curvatura adicional que siempre poseería un espaciotiempo vacío. En terminología moderna, equivaldría a proponer un estado cuántico de vacío con densidad de energía positiva y presión negativa; hoy llamaríamos a esto un estado de vacío inflacionario (figura 17). Einstein era consciente de que, en cosmología, un estado de vacío debía parecer el mismo a los diversos observadores que lo atravesaran a velocidades inferiores a la de la luz, de modo que no existiera un «estado de reposo» único. Esto significaba que, si tal espacio vacío poseía una densidad de energía positiva, debía tener necesariamente una presión negativa de igual magnitud. Esta presión negativa sería una especie de «succión universal». Si metiéramos un poco de ese estado de vacío inflacionario en los neumáticos de nuestro coche, colapsarían inmediatamente absorbidos por la presión negativa. Pero si en todo el espacio hubiera una presión negativa constante, no habría diferencias entre unas regiones y otras y no notaríamos nada; de hecho, en la sala donde se encuentra ahora el lector hay una presión de aire de en torno a 1 kilogramo por centímetro cuadrado que, al ser constante, no se nota.

Esa presión uniforme tiene, no obstante, una consecuencia. Las ecuaciones de Einstein nos dicen que la presión da lugar a efectos gravitatorios (algo que Newton no preveía). Una presión positiva, tal como la que habría en una estrella, produce una atracción gravitatoria; por lo tanto, una presión negativa debe generar una repulsión. Dado que existen tres dimensiones espaciales, la presión negativa del vacío inflacionario opera en tres direcciones, haciendo que el efecto gravitatorio repulsivo sea tres veces mayor que la atracción producida por la densidad de energía del vacío. Así pues, el estado de vacío inflacionario da lugar a una repulsión gravitatoria global.

Esta repulsión podría contrarrestar la atracción gravitatoria existente entre las estrellas y las galaxias y permitir que el universo sea estático. Por otra parte, y según los cálculos de Einstein, si la densidad media de la materia ordinaria del universo (estrellas y galaxias) fuese baja, la densidad de energía del vacío sería pequeña también, con lo que la circunferencia del universo triesférico sería grande. Por ejemplo, si la densidad media de las estrellas y las galaxias que salpican el espacio fuera aproximadamente de doscientos ochenta átomos de hidrógeno por metro cúbico, la circunferencia del universo estático de Einstein tendría unos diez mil millones de años luz. Esto haría que los efectos de la curvatura fuesen inapreciables a pequeña escala, al igual que una pequeña parcela en la Tierra nos parece plana en la práctica. De este modo, habríamos creído hasta ahora que nuestro universo se rige por las leyes de la geometría euclídea, cuando en realidad es curvo y cerrado, igual que nuestros antepasados imaginaban la Tierra plana hasta que descubrieron que era esférica.

Sin embargo, el modelo de Einstein planteaba problemas. Era inestable, como un lápiz puesto de punta. Su equilibrio no se podía mantener eternamente. A medida que las estrellas se consumían, generando radiación, la presión total del universo crecía, desplazando el modelo del equilibrio y precipitando un colapso.

Y los problemas no terminaban ahí. En 1929, Edwin Hubble demostró que el universo estaba expandiéndose. Cuando Einstein se enteró de la noticia, proclamó que la introducción de la constante cosmológica había sido «la mayor pifia de su vida». ¿Por qué? Porque si Einstein hubiera mantenido la versión inicial de su teoría —sin la dichosa constante—, ésta habría pronosticado, previamente a las observaciones de Hubble, la posible expansión o contracción del universo. En tal caso, el descubrimiento de Hubble no habría sido sino la suprema confirmación de la teoría de la gravitación de Einstein. Una verificación experimental a escala cósmica, mucho más impactante incluso que la de la predicción einsteiniana de que la luz se curvaba al pasar junto al Sol. En realidad, la predicción cosmológica también se anticipó al descubrimiento de Hubble; un joven matemático y meteorólogo ruso, Alexander Friedmann, publicó en 1922 y 1924 los modelos cosmológicos correctos, basados en la teoría original de Einstein (sin la constante cosmológica). Pero pocos conocían las soluciones de Friedmann antes del descubrimiento del astrónomo americano. No obstante, si el propio Einstein hubiera descubierto y anunciado esas soluciones en 1917, por ejemplo, todo el mundo científico se hubiera dado por enterado y a Einstein le habrían llevado a hombros por todo Nueva York cuando Hubble hubiera anunciado su descubrimiento. Lamentablemente para él, la historia siguió otro rumbo y hoy Einstein debe compartir la gloria con Hubble y Friedmann.