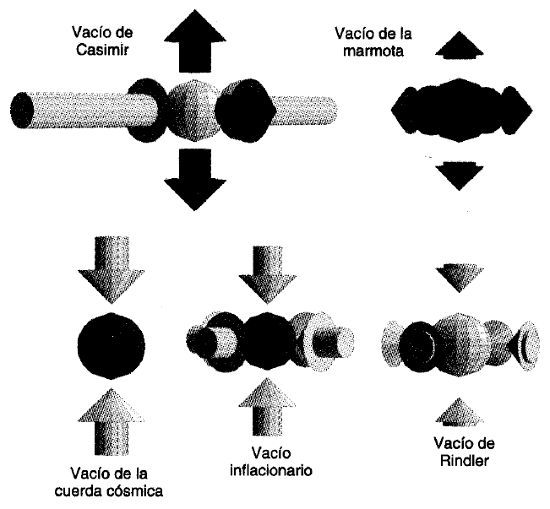
FIGURA 17. Diferentes tipos de vacío.
Para contar el resto de esta historia necesito hablarle al lector de los diferentes tipos de vacío, pues tienen un papel clave en los trabajos que desarrollamos juntos. No se trata del vacío que produce una aspiradora, sino el que resulta cuando de un recinto cerrado sacamos a la gente, los muebles, el aire y hasta las partículas elementales, fotones incluidos. Se supone que el vacío normal tiene densidad y presión nulas. Pero la mecánica cuántica nos dice que un espacio vacío no tiene por qué ser siempre un vacío con densidad de energía nula. En 1948, el físico holandés Hendrik Casimir observó que si colocamos dos placas conductoras muy juntas, el espacio entre ellas constituye un vacío con densidad de energía negativa, es decir, la cantidad de energía por centímetro cúbico es, realmente, inferior a cero. Tendríamos que añadir energía al sistema para que ésta fuera nula. La figura 17 representa el vacío de Casimir junto a otros tipos de vacío. En todos ellos, la densidad de energía está simbolizada por una esfera. Las esferas con sombreado claro representan densidades de energía negativas, mientras que las de color oscuro representan densidades de energía positivas. La presión en las distintas direcciones está indicada mediante flechas. Una flecha oscura apuntando hacia fuera representa una presión positiva, como la de los neumáticos de un coche. Una flecha clara apuntando hacia dentro simboliza una presión negativa, o succión. El vacío de Casimir presenta una presión positiva en las direcciones paralelas a las superficies de las placas y una elevada presión negativa en la dirección perpendicular a ellas, la cual tiende a succionar una contra otra. Esta fuerza ha sido medida en laboratorio (en primer lugar por parte de M. J. Sparnaay, en 1958, y de forma más precisa por S. K. Lamoreaux, en 1997). Así pues, sabemos que el vacío de Casimir existe. Cuanto más cerca estén las placas una de otra, más negativa será la densidad de energía en el espacio entre ellas.

FIGURA 17. Diferentes tipos de vacío.
La materia con densidad de energía negativa es algo muy especial. Abre la puerta a soluciones en la relatividad general que van desde los agujeros de gusano a los motores de distorsión. De hecho, Morris, Thome y Yurtsever han diseñado un agujero de gusano que aprovecha el efecto Casimir para mantener el túnel abierto. Para que funcione, este túnel ha de tener una circunferencia de mil millones de kilómetros. Cada una de las bocas debería estar cubierta por una placa de Casimir esférica, eléctricamente cargada. Las placas tendrían que estar separadas tan sólo 10-10 centímetros a través de un corto túnel que conectara ambas bocas (lo que concuerda con un límite encontrado por L. H. Ford y Thomas A. Roman para los agujeros de gusano, según el cual la materia con densidad de energía negativa ha de estar confinada en una capa muy fina dentro del túnel del agujero). Desde luego, la construcción de un agujero de gusano así sería una colosal obra de ingeniería. La masa total en juego es doscientos millones de veces la del Sol. Los astronautas que desearan pasar a través del agujero de gusano tendrían que evitar ser calcinados por la radiación, desplazada hacia el azul, que estaría incidiendo sobre las placas y deberían abrir una trampilla en cada una de éstas, a su debido tiempo, para cruzarlas. No es un asunto nada fácil, pero al menos el vacío de Casimir crea esa posibilidad.[31]
Los vacíos son también importantes para las cuerdas cósmicas. En el interior de una cuerda cósmica debe existir un estado de vacío con una densidad de energía positiva y una presión negativa en sentido longitudinal (figura 17), lo que crea esa tensión a lo largo de la cuerda que la convierte en algo parecido a una banda elástica. Dentro de una cuerda cósmica, por tanto, hay un estado muy peculiar de vacío de alta energía.[32]
Los estados de vacío desempeñan otro papel fundamental en la investigación sobre los viajes en el tiempo; un papel que también aparece en los estudios sobre el universo primitivo. Stephen Hawking pensaba que el estado de vacío podía estallar al intentar entrar en una máquina del tiempo, alterando la geometría del espacio-tiempo, creando una singularidad y malogrando nuestro ansiado viaje al pasado. Las ideas de Hawking sobre este tema se basan en lo que podría suceder en un espacio de Misner, un espacio-tiempo en el que originalmente no existe máquina del tiempo alguna, pero que desarrolla a la larga una región de viaje en el tiempo. Dicha región está separada de la que no permite dicho viaje por un horizonte de Cauchy, igual que en mi solución basada en cuerdas cósmicas. Podemos imaginar el espacio de Misner como una habitación infinita limitada por una pared frontal y una pared trasera. Nosotros viviríamos entre las dos paredes. Hay una puerta en cada una. Al salir por la puerta delantera entraríamos inmediatamente en la misma habitación desde la puerta trasera. El espacio de Misner está, por lo tanto, arrollado sobre sí mismo como un cilindro: las paredes delantera y trasera son en realidad las dos caras de un mismo tabique.
Si esta clase de espacio nos produce claustrofobia, las cosas pueden ser aún peores. Notamos que las dos paredes se están acercando la una a la otra. De hecho, se mueven a una velocidad constante y chocarán en el futuro, pongamos, en una hora. Es como estar atrapados en el compactador de basura de La Guerra de las Galaxias (las paredes se aproximan inexorablemente y nosotros nos hallamos en medio). Sin embargo, en el espacio de Misner es posible escapar. Basta con salir por la puerta delantera; como ya sabemos, volveremos a entrar en la misma habitación por la puerta de atrás. Ahora saldremos de nuevo por la puerta delantera y así una y otra vez. Como la distancia entre las paredes se va haciendo más pequeña, cada vez que atravesemos la habitación ganaremos velocidad con respecto a ella; de este modo pasaremos por la habitación una y otra vez, cada vez más deprisa. En poco tiempo, la pared delantera se nos acercará casi a la velocidad de la luz. Como la habitación entera se mueve más y más rápido respecto a nosotros, según la relatividad especial cada vez nos resultará más estrecha. Por otra parte, las paredes están realmente más cerca entre sí en cada ocasión. La combinación de ambos efectos hará que atravesemos la habitación un número infinito de veces en un tiempo finito, medido por nuestro reloj. ¿Adónde iremos a parar? Pues a una región de viaje en el tiempo, tras cruzar un horizonte de Cauchy. Ya no estaremos ni en nuestra habitación ni en el estado de Kansas, sino en un espacio-tiempo muy peculiar. La nueva región se parecerá a una hoja de papel en la que el pasado se halla abajo y el futuro, en la parte superior, y la cual habremos arrollado y pegado sus bordes, como en la figura 9. Podremos visitar los mismos sucesos repetidamente. El espacio de Misner es, desde luego, un tanto extraño, pero el cálculo de lo que en él sucede es relativamente sencillo. A menudo se toma como arquetipo de un espacio-tiempo en el que se crea una máquina del tiempo (como en los casos de los agujeros de gusano y las cuerdas cósmicas).
Los físicos William Hiscock y Deborah Konkowski, de la Universidad del estado de Montana, calcularon el tipo de yací o que sería aplicable a un espacio de Misner. Partieron del estado cuántico correspondiente al vacío normal y analizaron lo que pasaría si el recinto donde se halla aquél fuera enrollado y sus paredes delantera y trasera, pegadas la una a la otra. Resulta que las paredes actuarían entonces como placas de Casimir paralelas, por lo que Hiscock y Konkowski encontraron que dentro del recinto existiría un vacío de Casimir con densidad de energía negativa. Como ya hemos visto, si salimos de un recinto así por la parte delantera entraríamos automáticamente por la parte posterior. Y, conforme atravesamos el recinto una y otra vez, éste se hace progresivamente más angosto. La distancia entre ambas paredes —el perímetro del cilindro— es cada vez más pequeña. Cuanto más cerca está una pared de otra, más delgado es el cilindro y más negativa se hace la densidad de energía del vacío. Finalmente, justo antes de que saltemos a la región del viaje en el tiempo, dicha densidad crece exponencialmente hasta convertirse en un infinito negativo; lo cual produce una curvatura infinita del espacio —una singularidad—, lo que a su vez podría impedir nuestro acceso a la región del viaje en el tiempo.
Este hallazgo animó a Stephen Hawking a proponer su conjetura de la protección de la cronología: el hecho de que las leyes físicas parezcan siempre conspirar para impedir el viaje al pasado. Si el vacío cuántico crece exponencialmente en todos los casos, breando una singularidad cuando estamos a punto de entrar en una región del viaje en el tiempo, y a ello se unen otros efectos indeseables anteriormente mencionados, esa clase de regiones nunca serían accesibles para nosotros.
Decidí reexaminar los cálculos de Hiscock y Konkowski, confiando en que podría haber alguna forma de superar esas dificultades, de la misma manera que el descubrimiento por parte de Stephen Hawking de la radiación que lleva su nombre resolvió ciertos problemas de crecimiento exponencial del vacío en las proximidades del horizonte de sucesos de un agujero negro.
Le pedí a Li-Xin Li que calculara el estado de vacío en un espacio-tiempo más simple que incluyera el viaje en el tiempo, al que denominé espacio-tiempo de la marmota. En la película Atrapado en el tiempo, mencionada en el capítulo 2, el personaje interpretado por Bill Murray revivía una y otra vez el mismo día, que resultaba ser el Día de la marmota (el 2 de febrero). Todas las noches se acostaba y dormía hasta que sonaba el despertador a las 6:00. Para su consternación, descubría reiteradamente que eran las seis de la mañana del Día de la marmota y que volvía a estar donde había comenzado. El espacio-tiempo de la marmota resulta simplemente de «pegar» las 6:00 del martes con las 6:00 del miércoles, formando un cilindro (figura 9). En ese espacio-tiempo, cuando llegamos a las 6:00 del miércoles nos hallamos de nuevo en las 6:00 del martes. Nuestra línea de universo es una hélice que va rodeando el cilindro a medida que revivimos, una y otra vez, el mismo día. Si viviéramos ochenta años (29.220 días), nuestra línea de universo rodearía el cilindro 29.220 veces y, a medida que envejeciéramos, nos encontraríamos con 29.219 copias de nosotros mismos que abarcarían desde un bebé hasta un respetable anciano.
En ese escenario espaciotemporal podríamos jugar al fútbol contra nosotros mismos; de hecho, se podrían asumir todas las posiciones de ambos equipos y ser, a la vez, los espectadores. Podríamos ir al estadio, jugar la primera parte con un equipo, volver hacia atrás en el tiempo, jugar la segunda con el contrario y regresar aún muchas veces y sentarnos en las gradas a presenciar el partido, y en un asiento distinto cada vez. Nos parecería una sucesión normal de días, pero estaríamos presenciando los mismos acontecimientos repetidamente. El partido tendría siempre el mismo resultado: en realidad sería un único partido.[33]
Li-Xin Li halló que un vacío normal que envolviera el espacio-tiempo cilíndrico de la marmota tendría una densidad de energía y una presión positivas (figura 17). La densidad de energía y la presión serían pequeñas y, por lo tanto, no alterarían demasiado la geometría. No tendría lugar un crecimiento exponencial de la densidad de energía. Ningún estallido cuántico del vacío interferiría el viaje en el tiempo en las situaciones en las que dicho viaje siempre ha estado presente. En el espacio-tiempo de la marmota, el viaje en el tiempo está disponible en todas partes; todo suceso puede ser visitado de nuevo. No hay un horizonte de Cauchy que separe una región del viaje en el tiempo de otra en la que dicho viaje no es posible. Aun así, el vacío que Li-Xin Li encontró en el espacio-tiempo de la marmota era muy similar al que Hiscock y Konkowski habían hallado en la región del viaje en el tiempo del espacio de Misner.
Le pedí entonces a Li-Xin Li que calculara el vacío normal en el espacio de Misner, tal como habían hecho Hiscock y Konkowski.[34] Obtuvo los mismos resultados que ellos. ¿Había allí alguna solución de viaje en el tiempo que pudiera funcionar?
En nuestra siguiente comida juntos, Li-Xin Li afirmó:
«Tengo la respuesta». Había observado que, en una geometría dada, hay más de un estado de vacío posible, y en lugar de partir del vacío normal, comenzó sus cálculos desde el denominado vacío de Rindler.
El vacío de Rindler es el estado de vacío medido por observadores acelerados.[35]. Para entenderlo, debemos saber ante todo que un astronauta que haga funcionar los motores de su nave espacial, acelerándola en el seno de un vacío normal, detecta fotones. Esa radiación térmica se denomina radiación de Unruh, una radiación que no es visible si no se está acelerado. ¿De dónde vienen esos fotones? Su energía procede del vacío normal; es algo así como cuando alguien llena su bolsillo con dinero real tomando un préstamo y contrayendo una deuda, La energía que el astronauta «toma prestada» del vacío le hace observar un vacío con una densidad de energía inferior a cero, un estado de vacío llamado vacío de Rindler. El vacío de Rindler tiene una densidad de energía y una presión negativas (figura 17), que contrarrestan exactamente la densidad de energía y presión positivas de la radiación de Unruh observada por el mismo astronauta. De este modo, la densidad de energía total y la presión total son nulas, tal como corresponde al estado de vacío normal que mediría un observador no acelerado como nosotros. El astronauta detecta fotones, nosotros no. Disentfremos sobre la clase de vacío que nos rodea y si hay fotones presentes o no, pero ambos estaremos de acuerdo acerca de la densidad de energía total. El vacío normal que vemos nosotros equivale al vacío de Rindler que él observa sumado a la radiación de Unruh, sólo detectada por él. Si el observador acelerado no apreciara radiación alguna, concluiría que la densidad de energía es realmente inferior a cero y que se halla en un universo con un vacío de Rindler puro. El vacío de Rindler es bien conocido (al menos, para los físicos) a la hora de describir el estado de vacío para observadores acelerados (para detalles adicionales acerca de este tipo de vacío, véase el apartado Notas).
Un vacío de Rindler en la región del viaje en el tiempo da lugar a una densidad de energía y a una presión negativas. Pero como el espacio-tiempo está arrollado en la dirección tiempo, se añaden a ello una densidad de energía y una presión positivas (tal como ocurría en el espacio-tiempo de la marmota). Con los parámetros adecuados, ambos efectos casi se cancelan mutuamente, dejando un vacío con densidad de energía y presión nulas, como el vacío normal. Para que así sea, las paredes delantera y trasera del espacio de Misner deben acercarse la una a la otra al 99,9993% de la velocidad de la luz.
Se trataba de una hermosa solución. Li y yo nos dimos un apretón de manos. Ese vacío arrollado de Rindler tenía densidad de energía y presión nulas a todo lo largo del espacio de Misner —tanto en la región del viaje en el tiempo como en la que el viaje no es posible— y resolvía, por lo tanto, las ecuaciones de Einstein de manen exacta.[36] Era una solución autoconsistente: la geometría, que incluía el viaje en el tiempo, generaba el vacío cuántico adecuado y ese estado de vacío, mediante las ecuaciones de Einstein, producía a su vez la geometría de partida. La solución constituía un contraejemplo de peso a la conjetura de la protección de la cronología, ya que se refería al propio ejemplo que había llevado a formularla.
Enseguida entendimos los dos que la solución podía ser adaptada para producir un estado de vacío autoconsistente con destino al modelo de universo primitivo con viaje en el tiempo incluido en el que estábamos trabajando. El paso siguiente era demostrarlo. Y lo hicimos. Completar nuestro artículo sobre cosmología podía llevar meses, así que decidimos escribir un artículo aparte sobre el espacio de Misner y enviarlo enseguida al Physical Review Letters. Li-Xin Li figuraba como primer autor, pues era él quien había hecho el descubrimiento decisivo.[37] Enviamos el texto el 5 de septiembre de 1997, añadiendo una frase críptica en la que afirmábamos disponer también de una solución autoconsistente para un tipo de espacio que podría ser aplicable a una solución para el universo primitivo que implicaba el viaje en el tiempo. Confiábamos en que la frase estableciera nuestra prioridad sobre la idea, sin desvelarla todavía. Mientras tanto, trabajaríamos frenéticamente en completar los cálculos para nuestro artículo sobre la creación del universo.
En el ejemplar de noviembre de Classical and Quantum Gravity apareció un nuevo artículo de Michael J. Cassidy, alumno de Stephen Hawking, en el que se demostraba que tenía que existir un estado de vacío para el espacio de Misner que tuviera densidad y presión nulas en todos los puntos. Cassidy había llegado a esta conclusión razonando sobre el vacío existente alrededor de una cuerda cósmica. No sabía de qué estado se trataba; simplemente afirmaba que tenía necesariamente que existir y ser diferente del que habían usado Hiscock y Konkowski. Por otra parte, el estado aparecía cuando las paredes delantera y trasera se aproximaban entre ellas al 99,9993% de la velocidad de la luz. ¡El estado cuántico de vacío cuya existencia defendía Cassidy era claramente el que nosotros habíamos hallado! Y se nos había adelantado al publicarlo. Nos pareció que era sólo cuestión de tiempo el que alguien más encontrara nuestra solución, así que colocamos inmediatamente nuestro artículo sobre el espacio de Misner en la web destinada a borradores de astrofísica (www.lanl.gov/archive/astro-ph), donde todo el mundo pudiera leerlo. Luego, redoblamos nuestros esfuerzos para tener terminado el artículo de cosmología lo antes posible (sólo descansamos el día de Navidad). Lo presentamos vía Internet al Physical Review, enviándolo por correo electrónico justo al acabar el año, el 30 de diciembre de 1997. Nuestro artículo sobre el espacio de Misner fue publicado en Physical Review Letters el 6 de abril de 1998 y nuestro artículo de cosmología —titulado «¿Puede el Universo crearse a sí mismo?»— apareció el 29 de mayo de 1998 en la versión electrónica del Physical Review, y el 15 de julio del mismo año en la versión en papel.[38] En nuestro artículo de cosmología utilizábamos la idea del viaje en el tiempo para abordar una de las cuestiones más antiguas y misteriosas de la cosmología: la de la causa primera.