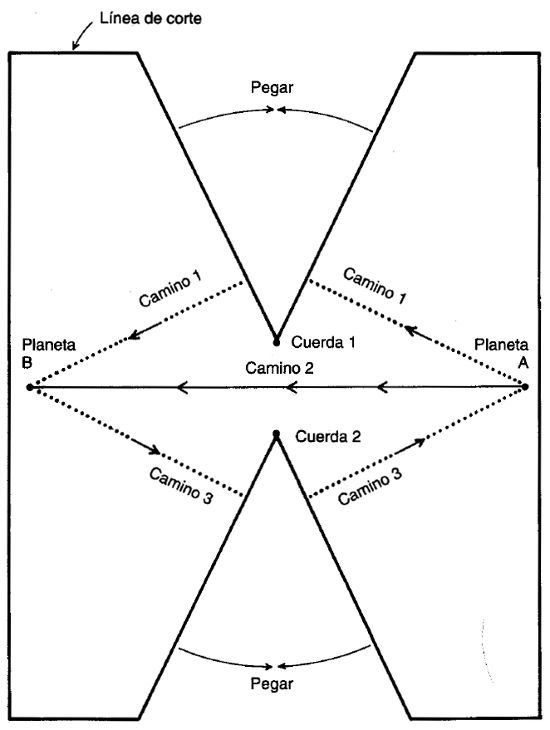
FIGURA 11. Espacio alrededor de dos cuerdas cósmicas.
Mi idea de una máquina del tiempo para viajar al pasado se basa en una solución exacta de las ecuaciones de Einstein que publiqué en 1991. He aquí el escenario. En primer lugar, imaginemos dos cuerdas cósmicas rectas e infinitamente largas, como si fueran dos mástiles paralelos. Curiosamente no se atraen gravitatoriamente entre sí, simplemente permanecen inmóviles. Esto se debe a que, aunque tienen una densidad enorme, se hallan también bajo tensión, como si fueran gomas elásticas tirantes. Esa tensión, que actúa sobre ambas, es producida por una presión negativa, o succión, en el interior de la cuerda. El efecto gravitatorio repulsivo de esta presión negativa contrarresta exactamente la atracción gravitatoria que se produce por la masa que contiene la cuerda. Así pues, si colocamos las dos cuerdas cósmicas una junto a otra y en reposo, se quedarán en la misma posición.
Para visualizar la sección que resulta de cortar el espacio-tiempo perpendicularmente a las dos cuerdas, el lector puede copiar la figura 11 y recortar su perfil según se indica. En el papel hay dos puntos que representan las cuerdas cósmicas pero, como en el ejemplo de la pizza, faltan dos porciones cuyo vértice se halla justamente en ellos. Si colocamos un par de lápices verticales sobre los puntos identificados como cuerda 1 y cuerda 2, las «cuerdas» serán una especie de mástiles perpendiculares al papel y la figura mostrará una sección horizontal de la geometría del entorno. A continuación debemos unir mediante cinta adhesiva los dos bordes en y de la parte superior y luego hacer otro tanto los de la y inferior. El espacio-tiempo que resulte parecerá un barco de papel.
Imaginemos ahora dos planetas, A y B, a izquierda y derecha de las cuerdas. Supongamos que nos hallamos en el planeta A y deseamos visitar el planeta B. Podríamos hacerlo viajando directamente a dicho planeta a lo largo del camino 2, que pasa entre las dos cuerdas cósmicas. Ésa es la trayectoria geodésica —un camino recto posible entre los planetas A y B—. Pero existe otro camino recto entre A y B, el camino 1, que pasa por encima de la cuerda cósmica 1. Si medimos con cuidado, veremos que la distancia total desde el planeta A hasta el planeta B a lo largo del camino 1 es ligeramente más corta que la correspondiente al camino 2, debido a la porción que falta. El camino 1 es un atajo entre ambos planetas. Si enviamos un rayo de luz de A a B a través del camino 2, podríamos tomar nuestra nave espacial —que viaja al 99,999999% de la velocidad de la luz— y adelantar a dicho rayo mediante el camino 1 (rodeando la cuerda 1). Cuando lleguemos al planeta B, el rayo de luz que muestra nuestra partida no habrá llegado todavía. Si miramos hacia el planeta A a través del camino 2, nos veremos a nosotros mismos preparándonos para salir de viaje.
Interesante, ¿no? Quizá si nos damos prisa, aún tengamos tiempo de regresar y vemos partir. De hecho, existe un observador (que llamaremos Cosmo) viajando rápidamente en una nave espacial a lo largo del camino 2 desde A hacia B, que piensa que nuestra partida de A y nuestra llegada a B son sucesos simultáneos. ¿Por qué? Porque al haber adelantado al rayo de luz que viaja por el camino 2, nuestra partida y nuestra llegada son dos sucesos separados a lo largo de ese camino por más años luz en el espacio que años en el tiempo. Como esto da lugar a una separación tipo espacio, Cosmo ve dichos sucesos como si tuvieran una separación en el espacio, pero ninguna separación en el tiempo.
Llegados aquí, me di cuenta de que se podía dividir exactamente el espacio-tiempo de la figura 11 mediante un corte preciso a lo largo del camino 2 (imagínese el tajo seco de una cuchilla de carnicero). Si lo hacemos en nuestro modelo, el espacio-tiempo quedará separado en dos mitades: la superior, que contiene la cuerda 1, y la inferior, que contiene la cuerda 2. Como el espacio-tiempo estático en su conjunto podría ser extraído de un espacio-tiempo plano eliminando simplemente dos porciones, la frontera (el corte de la cuchilla) entre las dos mitades del espacio-tiempo también es plano. La frontera no tiene una curvatura intrínseca y no está deformada. En otras palabras, la mitad superior de la figura 11 puede deslizarse hacia la derecha a gran velocidad (aunque menor que la de la luz) y la inferior, en sentido opuesto y a una velocidad igualmente elevada, sin que los bordes de ambas dejen de ajustar perfectamente el uno con el otro conforme se mueven. Haciendo uso de esta idea, elaboré una geometría en la que la cuerda 1 se mueve rápidamente hacia la derecha, la cuerda 2 hace lo propio hacia la izquierda y las dos mitades del espacio-tiempo se ajustan perfectamente la una a la otra. De este modo, las ecuaciones de Einstein se cumplen exactamente en ambas mitades y a lo largo de la frontera entre ellas. Para estar seguros de que nuestro amigo Cosmo no resulta partido en dos durante el proceso, imaginémosle un poco más arriba de esa frontera, ligeramente en la parte superior, de modo que se mueva hacia la derecha al igual que la cuerda 1. De hecho, moveremos la mitad superior del diagrama a la velocidad exacta necesaria para compensar la velocidad inicial de Cosmo y conseguir que se halle en reposo.

FIGURA 11. Espacio alrededor de dos cuerdas cósmicas.
Imaginemos ahora a Cosmo en reposo en el camino 2, en un punto intermedio entre los planetas A y B. Nuestro amigo ve la cuerda 1 moviéndose hacia la derecha a una velocidad cercana a la de la luz y la cuerda 2 haciendo lo mismo hacia la izquierda. Si viajamos entonces entre ambos planetas tomando el atajo que rodea la cuerda 1, Cosmo verá nuestra partida del planeta A a mediodía y nuestra llegada al planeta B, también a mediodía. Lo hemos conseguido viajando en contra del movimiento de la cuerda 1 y usando el camino 1 (figura 12). Como la cuerda 2 se mueve en sentido opuesto, podemos repetir el truco al regresar al planeta A, viajando por el camino 3 y moviéndonos en contra de la cuerda 2. Así pues, según las observaciones de Cosmo, podemos dejar el planeta B a mediodía y estar de vuelta en el planeta A también a mediodía. Como Cosmo piensa que nuestra partida de A y nuestra llegada a ese punto han ocurrido en el mismo lugar (el planeta A) y en el mismo momento (a mediodía), para él son un suceso único.
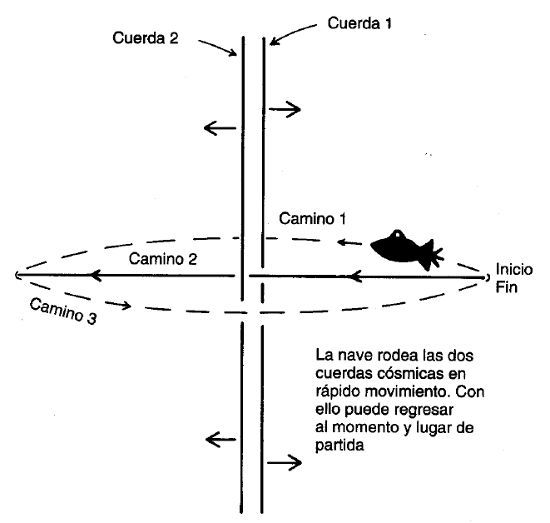
FIGURA 12. Viajando a un suceso del pasado.
¿Cómo veríamos nosotros el viaje? Se parecería a la historia descrita en el capítulo 1. Cuando lleguemos al aeropuerto del planeta A a mediodía, una versión algo mayor de nosotros mismos nos estrechará la mano y nos dirá: «Hola. He rodeado las cuerdas una vez». Nosotros replicaremos:
«¿De veras?». Entonces subiremos a nuestra nave espacial y volaremos hacia el planeta B, rodeando, a través del camino 1, la cuerda 1 que viene rápidamente hacia nosotros. Luego regresaremos al planeta A por el camino 3, rodeando ahora la cuerda 2 que se nos acerca rápidamente. Al llegar a mediodía a nuestro planeta encontraremos a nuestro yo más joven a punto de partir, le estrecharemos la mano y le diremos: «Hola. He rodeado las cuerdas una vez». Habremos llevado a cabo un viaje a través del tiempo a un suceso de nuestro pasado.
La solución de la cuerda cósmica en movimiento es lo suficientemente enrevesada como para permitirnos viajar en sentido contrario alrededor de las dos cuerdas móviles, avanzando siempre hacia el futuro, y seguir llegando a casa en el momento de partir. Esto sólo es posible porque el espacio-tiempo es curvo y no obedece las leyes de la geometría euclídea. La situación siempre me ha recordado el grabado de Escher Subiendo y bajando, que representa a un grupo de monjes sobre una escalera en lo alto del monasterio (figura 13). Los monjes que marchan en el sentido de las agujas del reloj siempre están subiendo; cada escalón está más arriba que el anterior. Pero cuando han dado la vuelta completa al patio se encuentran en el punto de partida. Normalmente, una escalera de este tipo sería una hélice que no se cortaría a sí misma, pero Escher ha conseguido el milagro mediante un truco de perspectiva. Para descubrirlo, obsérvese que la escalera dobla cuatro veces en ángulo recto alrededor del patio, lo que implica que éste debería ser rectangular; sin embargo, la parte superior izquierda es mucho más corta que la inferior derecha. El patio de Escher no responde a las leyes de la geometría euclídea, según las cuales los lados opuestos de un rectángulo tienen igual longitud. Lo que Escher consigue mediante un truco de perspectiva, las cuerdas cósmicas lo logran curvando la geometría del espacio-tiempo.

FIGURA 13. Subiendo y bajando (1960), de MC. Escher.
Para permitir el viaje al pasado, las cuerdas cósmicas con una masa por unidad de longitud de diez mil billones de toneladas por centímetro han de moverse en sentidos opuestos al 99,999999996% de la velocidad de la luz como mínimo.[19] En el universo se han observado protones de alta energía moviéndose así de deprisa, por lo que cabe deducir que tales velocidades son posibles.
Cuando hallé esta solución, mi entusiasmo fue grande. Empleaba solamente materia con densidad positiva, moviéndose a una velocidad inferior a la de la luz. Las soluciones basadas en agujeros de gusano, por el contrario, requieren materiales más exóticos (masa con densidad negativa, es decir, algo que pese menos que la nada). Comprobé la solución unas cuantas veces, la llevé al papel y la envié al Physical Review Letters, una de las publicaciones más ágiles del mundo. No se lo dije a nadie y esperé los comentarios de los críticos. Me llegaron dos informes que aprobaban mi trabajo y sugerían sólo un par de adiciones menores. Finalmente, el artículo apareció el 4 de marzo de 1991. Fui al Instituto de Estudios Avanzados —el antiguo lugar de trabajo de Einstein— para hacerme con una copia del artículo de la revista, aprovechando que el Instituto suele recibir los ejemplares uno o dos días antes que la biblioteca de la Universidad de Princeton. Tomé la copia para mostrársela a John Wheeler, el físico de Princeton que inventó el término agujero negro. Resultó que Kip Thome había acudido a Princeton para dar una conferencia aquel mismo día sobre su investigación en tomo a los viajes en el tiempo mediante agujeros de gusano, por lo que le enseñé también la copia a él. En las películas, los científicos siempre cuentan sus descubrimientos a otros científicos garabateando ecuaciones en una pizarra. Yo, en cambio, lo hice a base de recortables.
Aquel día, al término de su conferencia, Thorne mencionó mi nuevo resultado. En los pasillos y cafeterías de los departamentos científicos, las ideas y los artículos de investigación se someten continuamente a discusión y debate. Aunque se admitía que mi artículo representaba una solución notable de las ecuaciones de Einstein, se produjo el lógico revuelo, pues algunos escépticos dudaban sobre la posibilidad de que alguna vez se llevaran a cabo los viajes en el tiempo en nuestro universo. Alex Vilenkin, de la Universidad de Tufts, me invitó a dirigirme al grupo relativista de Tufts-Harvard-MIT en Boston. Para mi satisfacción, en la sala había muchos científicos eminentes. Estaba Bill Press, de Harvard, y Alan Guth había traído a sus colegas del MIT Edward Farhi y Sean Carroll.
El mismo día apareció en la revista Time un artículo de Michael Lemonick sobre mis investigaciones. Incluía una foto mía en la que sostenía dos cuerdas y las pasaba alrededor de una nave espacial de juguete que mi hija de siete años me había prestado. Años atrás, había aparecido en Newsweek con una cuerda en la mano con el objetivo de ilustrar la solución de una única cuerda. Esto explica el hecho, por otra parte curioso, de que haya una foto mía en Newsweek sujetando una cuerda y otra en Time sosteniendo dos.
Guth y sus dos colegas del MIT hallarían posteriormente algunas propiedades interesantes de mi solución, entre las cuales está el hecho de que, en el momento de regresar al planeta A, la nave espacial habría girado 360 grados y adquirido un impulso adicional de velocidad.[20]
Kip Thorne tuvo noticia de mi solución en Caltech cuando uno de sus alumnos, Curt Cutler, encontró una propiedad aún más intrigante. Cutler se propuso comprobar si cualquier suceso de mi espacio-tiempo podía ser visitado dos veces por un viajero del tiempo. Todos los sucesos que un viajero podría visitar en dos ocasiones, como nuestra partida del planeta A, pertenecerían a una región geométrica que permite los viajes en el tiempo. Todo suceso al que ningún viajero pudiera regresar jamás pertenecería a una región en la que el viaje en el tiempo no es posible. Cutler encontró que mi espacio-tiempo incluía ambos tipos de zona: una región alrededor de las cuerdas, en la que el viaje al pasado es posible, rodea otra región con forma de reloj de arena, en la que el viaje al pasado es imposible (figura 14). En este diagrama espaciotemporal se representan horizontalmente dos dimensiones espaciales, mientras que el tiempo aparece en el eje vertical, con el futuro hacia arriba. La cuerda 1 se mueve hacia la derecha con el tiempo; su línea de universo es una recta inclinada hacia arriba a la derecha. Cuanto más hacia el futuro, más a la derecha se encontrará la cuerda. La cuerda 2, que se mueve en sentido opuesto, tiene una línea de universo inclinada hacia arriba a la izquierda. En el pasado lejano (la parte inferior de la imagen), la cuerda 1 estaba a la izquierda de la cuerda 2. Ambas se cruzan en el centro y, en un futuro lejano, la cuerda 1 se hallará a la derecha de la cuerda 2. La superficie que separa la región donde el viaje al pasado es posible de la región donde no lo es se parece a un diábolo y es denominada horizonte de Cauchy (en honor del matemático francés del siglo XIX Augustin-Louis Cauchy, quien desarrolló una parte fundamental de la matemática asociada). Los sucesos que se sitúan dentro de la región con forma de reloj de arena no pueden ser visitados de nuevo. Los sucesos que se hallan fuera, alrededor de las cuerdas, podrían ser visitados otra vez por un viajero del tiempo.
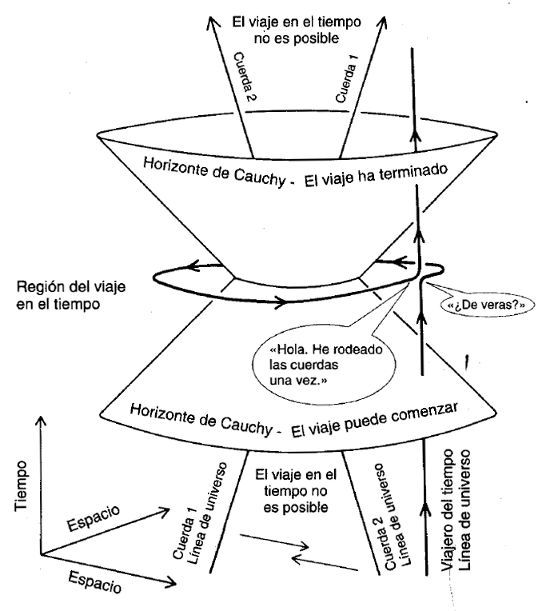
FIGURA 14. La región del viaje en el tiempo alrededor de dos cuerdas cósmicas.
Nuestra línea de universo —la del viajero del tiempo— también aparece representada. Comienza en la parte inferior derecha del diagrama, cuando aún estamos en el planeta A. La línea asciende en vertical, ya que no nos movemos en el espacio, sino sólo hacia delante en el tiempo. Entonces partimos y rodeamos las cuerdas: el bucle circular horizontal. Cuando regresamos al planeta A, decimos: «Hola. He rodeado las cuerdas una vez». Tras ello, nos quedamos simplemente en el planeta y nuestra línea de universo continúa en vertical hacia arriba. El suceso por el cual nos encontramos y nos saludamos a nosotros mismos se halla en la región del viaje en el tiempo. Curiosamente, el horizonte de Cauchy con forma de reloj de arena limita dicha región tanto en el pasado como en el futuro. Obsérvese que nuestra línea de universo viene de abajo, de un pasado lejano perteneciente a la región en la que el viaje en el tiempo no es posible. En ese pasado lejano, las dos cuerdas cósmicas están tan separadas que a un viajero que partiera del planeta A le llevaría tanto tiempo rodearlas que regresaría siempre después de su partida. Cuando las cuerdas se aproximan lo suficiente y nuestra línea de universo traspasa el horizonte de Cauchy y penetra en la región del viaje en el tiempo, se hace de pronto posible regresar y estrechar la mano a un yo más joven. Se ha creado una máquina del tiempo y, durante un cierto periodo, nuestra línea de universo permanecerá en la región en la que cabe hacer uso de ella. Finalmente, dicha línea atravesará de nuevo la superficie límite y la posibilidad de viajar en el tiempo se esfumará para nosotros. La máquina del tiempo habrá desaparecido. Las cuerdas volverán a estar tan separadas que, siempre que las rodeemos, retomaremos después de nuestra partida. El viaje en el tiempo es posible sólo en el intervalo de existencia de la máquina.
Esto responde a la famosa cuestión de Stephen Hawking de por qué no nos han invadido los turistas del futuro. Se debe, simplemente, a que nadie ha construido una máquina del tiempo todavía. Dicho de otra manera, si se construyera una máquina del tiempo en el año 3000, alguien podría hacer uso de ella para ir desde el año 3002 hasta el año 3001, pero nunca podría regresar a 2001, ya que el año es anterior al de la construcción de la máquina. Las máquinas del tiempo como la mía —basadas en cuerdas cósmicas— o la de Kip Thome —basadas en agujeros de gusano—, que implican una torsión del espacio-tiempo, incluyen regiones espaciotemporales en las que el viaje en el tiempo no es posible. Si hasta la fecha no se ha fabricado ninguna máquina de esa clase, quienes hoy día nos hallemos en la Tierra no podremos visitar nuestro pasado. Por otra parte, todos los sucesos de los que tenemos noticia se hallan dentro de nuestro cono de luz pasado, antes también de la región del viaje en el tiempo. Así pues, no hubo viajeros del tiempo que presenciaran el asesinato de Kennedy en 1963. Y al igual que ese importante suceso, también nosotros pertenecemos a un espacio-tiempo anterior al de la creación de la primera máquina del tiempo, por lo que ningún viajero del tiempo puede visitarnos. No obstante, los trabajos de Cutler muestran que, aunque los observadores examinen cuidadosamente su propio pasado y no encuentren en él evidencia alguna de la existencia de viajeros del tiempo, el hecho no les permite concluir que nunca se cruzarán con ellos en el futuro. En cualquier momento, un observador podría cruzar un horizonte de Cauchy y encontrarse de repente en una región donde los viajes en el tiempo son posibles y en la que los viajeros del futuro hicieran su inesperada aparición.