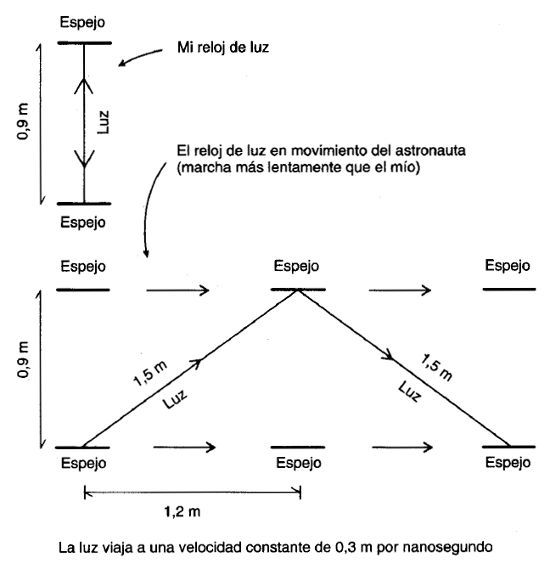
FIGURA 3. Diversos relojes de luz
Uno de los primeros teoremas derivados por Einstein de sus dos postulados viene a decir que si un astronauta nos rebasara a gran velocidad, veríamos que sus relojes avanzan más despacio que los nuestros. Einstein demostró el teorema mediante un ingenioso experimento mental: imaginó un reloj muy simple, en el que un rayo de luz rebota entre dos espejos. El reloj hace «tic» cada vez que el rayo alcanza uno de ellos. Como la luz viaja a trescientos mil kilómetros por segundo, tardaría aproximadamente 1 nanosegundo (una milmillonésima de segundo) en recorrer 30,48 centímetros. Si separamos los espejos algo menos de 1 metro, nuestro reloj de luz haría un tic cada 3 nanosegundos (figura 3). Supongamos ahora que nos adelanta un cohete volando a una velocidad equivalente al 80% de la de la luz. A bordo va un astronauta con un reloj de luz de dimensiones idénticas a las del nuestro. [7]
Si al pasar el astronauta observamos su reloj, veremos rebotar su rayo de luz arriba y abajo, describiendo una trayectoria en zigzag conforme los dos espejos se desplazan de izquierda a derecha (figura 3). Cuando el rayo de luz va desde el espejo inferior al superior, nos parece que viaja en diagonal hacia arriba a la derecha, ya que, al alcanzar el espejo superior, éste se halla más a la derecha de donde estaba en el instante inicial. Cuando el rayo va hacia el espejo inferior, parece moverse en diagonal hacia abajo a la derecha por la misma causa. Si medimos la longitud de estas trayectorias diagonales, es evidente que el resultado supera los 0,9 metros. Como, forzosamente, la luz viaja para todos a 0,3 metros por nanosegundo (tal como afirma el segundo postulado), el intervalo entre tics en el reloj del astronauta es, para nosotros, superior a 3 nanosegundos.

FIGURA 3. Diversos relojes de luz
¿Cuánto atrasa el reloj del astronauta? Podemos calcularlo. Si el astronauta viaja al 80% de la velocidad de la luz con respecto a nosotros, la distancia en diagonal que recorre la luz entre un espejo y otro resulta ser 1,5 metros. Podemos construir un triángulo rectángulo cuyos lados midan 1,5, 1,2 y 0,9 metros. Los antiguos egipcios ya conocían esto. El lado horizontal tendría 1,2 metros, el vertical, 0,9 y el diagonal, 1,5. Mientras el rayo de luz viaja en diagonal hacia arriba recorriendo 1,5 metros, el espejo inferior, moviéndose al 80% de la velocidad de la luz, se desplazará horizontalmente a la derecha una distancia de 1,2 metros exactamente.
Como la luz recorre 0,3 metros cada nanosegundo, transcurren 5 nanosegundos entre cada tic del reloj del astronauta. Después de 15 nanosegundos, habremos observado 3 tics en su reloj. Pero, después de esos mismos 15 nanosegundos, habremos observado 5 en el nuestro. Por cada 5 tics de nuestro reloj, el suyo sólo efectúa 3. Así pues, su reloj va más despacio que el nuestro.
Ahora viene lo más notable. El astronauta podría usar los latidos de su corazón como una especie de reloj. Sus espejos en paralelo (con un rayo de luz rebotando entre ellos) y su corazón son simplemente dos relojes en reposo el uno respecto al otro, por lo que existirá una relación fija entre sus respectivos ritmos. Cuando observamos que el astronauta se desplaza respecto a nosotros al 80% de la velocidad de la luz, no sólo vemos que su reloj de luz hace tres tics por cada cinco del nuestro, su corazón late también más despacio en la misma proporción; razón por la cual envejecerá más lentamente que nosotros. Cuando hayamos envejecido cinco años, veremos que él sólo habrá envejecido tres. Los relojes biológicos y los relojes de luz necesariamente atrasan del mismo modo; en caso contrario, el astronauta podría deducir que es él quien se está moviendo, lo cual violaría el primer postulado.
Estos efectos se hacen más espectaculares a medida que la velocidad del astronauta se aproxima a la de la luz. El resultado depende del cociente v/c, donde v es la velocidad del astronauta con respecto a nosotros y c es la velocidad de la luz. ¿Recuerda el lector las clases de geometría en el colegio? Uno de los tópicos fundamentales era el teorema de Pitágoras: en un triángulo rectángulo, la suma de los cuadrados de los catetos (los lados vertical y horizontal) es igual al cuadrado de la hipotenusa (el lado en diagonal). Al tiempo que la luz se mueve 0,3 metros en diagonal, el reloj del astronauta se desplaza a la derecha una distancia igual a 0,3 metros multiplicado por el cociente (v/c), creando dos lados de un triángulo rectángulo. Si la hipotenusa fuera igual a 0,3 metros y el cateto horizontal (v/c) metros, según el teorema de Pitágoras, el cateto vertical valdría [0,3 − (v/c)2]1/2 [8] (elevando al cuadrado la raíz cuadrada de [0,3 − (v/c)2] se obtiene [0,3 − (v/c)2]; si a ello le sumamos (v/c)2 obtenemos 0,3, la hipotenusa). El recorrido vertical que vemos hacer al rayo de luz hacia el espejo superior no es, por consiguiente, 0,3 metros, sino 0,3 metros multiplicado por [0,3 − (v/c)2]1/2. Como el rayo debe ascender 0,9 metros antes de que veamos hacer tic al reloj del astronauta, el ritmo de este último será [0,3 − (v/c)2]1/2 veces el del nuestro. Si el astronauta pasa junto a nosotros al 99,995% de la velocidad de la luz, observaremos que su reloj marcha cien veces más despacio. Cuando hayan transcurrido mil años en la Tierra, quienes desde ella observen al astronauta verán que ¡sólo ha envejecido diez!
El viaje al futuro es posible por el hecho de que los observadores que se mueven unos respecto a otros tienen percepciones distintas del tiempo. Estos observadores pueden disentir incluso sobre la simultaneidad de los sucesos; un fenómeno que desempeñará un importante papel a la hora de entender cómo podría materializarse el viaje al pasado.
Imaginemos que un astronauta pasa junto a nosotros al 80% de la velocidad de la luz y que observamos que su nave tarda 22,5 nanosegundos en pasar de izquierda a derecha. A la velocidad de 0,24 metros por nanosegundo, en ese tiempo se desplaza 5,4 metros respecto a nosotros, por lo que diremos que su nave tiene una longitud de 5,4 metros. Como vemos que el tripulante está sentado en el centro de la nave, afirmaremos que se halla a 2,7 metros del extremo delantero de ésta y a otros tantos de la cola. El astronauta envía dos señales luminosas a sendos espejos ubicados en los extremos de la nave. La luz se refleja en ellos y el astronauta recibe las dos señales de vuelta al mismo tiempo. Como los espejos se hallan equidistantes de él y la velocidad de la luz ha de ser trescientos mil kilómetros por segundo cuando él la mide, el astronauta afirmará que las señales luminosas alcanzan simultáneamente los dos espejos. Para nosotros, la señal luminosa enviada hacia la cola de la nave tarda 5 nanosegundos en llegar allí. En ese tiempo, la señal viaja 1,5 metros hacia la izquierda y la nave (que se mueve a 4/5 partes de la velocidad de la luz) se desplaza 1,2 metros hacia la derecha, completando entre ambas la distancia de 2,7 metros.
Pero ¿qué ocurre con la señal que el astronauta envía hacia el morro de la nave? Debe alcanzar el espejo delantero, que tiende a huir de ella. Observaremos que la luz tarda en alcanzarlo 45 nanosegundos exactamente. El morro se halla inicialmente a 2,7 metros del punto de partida de la señal. Durante 45 nanosegundos, la luz recorre 13,5 metros, mientras el morro de la nave avanza el 80% de esa distancia, es decir, 10,8 metros, con lo que los 2,7 metros de partida se compensan. Así pues, observamos que la señal que el astronauta envía hacia atrás tarda en llegar a su destino sólo 5 nanosegundos, mientras que la que envía hacia delante tarda cuarenta y cinco. Para nosotros, la señal enviada hacia atrás alcanza su espejo antes que la enviada hacia delante.
Cuando la señal luminosa llega al espejo posterior, es reflejada y vuelve hacia el astronauta. ¿Cuánto tardaría en regresar, según nosotros? En este caso, el astronauta lleva una ventaja de 2,7 metros y tiende a alejarse, por lo que, conforme al razonamiento de antes, el recorrido de vuelta tardaría 45 nanosegundos. Vemos, pues, cómo la señal viaja hacia atrás, se refleja y alcanza al astronauta de nuevo tras 5 más 45, es decir, un total de 50 nanosegundos. ¿Qué hay de la señal enviada hacia delante? Sólo le hacen falta 5 nanosegundos para regresar al astronauta, puesto que, tras reflejarse, la luz recorre 1,5 metros mientras aquél avanza otros cuatro a su encuentro. De nuevo el recorrido total dura 50 nanosegundos.
Observaremos, pues, que los rayos de luz retoman al astronauta a la vez, exactamente igual que él. Pero él percibe que los rayos alcanzan simultáneamente los espejos anterior y posterior, ya que se halla en el centro de la nave y se considera en reposo. Nunca coincidiremos en si la llegada de la señal a cada uno de los espejos se produjo simultáneamente o no. La cuestión no radica en quién de nosotros está equivocado, sino en que cada uno tiene su propio marco de referencia.
Hay otro punto notable aún. Hemos dicho que el astronauta «recupera» las señales luminosas al cabo de 50 nanosegundos. Pero sabemos que se está moviendo al 80% de la velocidad de la luz, con lo que sus relojes marcharán al 60% del ritmo al que avanzan los nuestros y le dirán que sólo han transcurrido 30 nanosegundos desde que envió las señales hasta que las recibió de vuelta. Él se considera en reposo y sabe que la luz viaja a 0,3 metros por nanosegundo, con lo que le parecerá que aquélla tarda 15 nanosegundos en alcanzar cualquiera de los dos espejos y otro tanto en regresar; de este modo llegará a la conclusión de que el morro y la cola de su nave se hallan a 4,5 metros cada uno de donde él se encuentra y de que la nave, por lo tanto, tiene 9 metros de longitud. Pero recordemos que habíamos medido esa longitud y, para nosotros, el resultado era de 5,4 metros. Así pues, afirmaremos que su nave tiene sólo el 60% de la longitud que él mide. Se trata del mismo factor que indica cuán lento va su reloj respecto al nuestro. Las varas de medir que el astronauta transporte en una dirección paralela a su trayectoria nos parecerán comprimidas. Si no fuera así, los relojes de luz transportados por este mismo astronauta en posición paralela o perpendicular a dicha trayectoria marcharían a ritmo diferente, y él podría concluir que se halla en movimiento, lo cual va en contra del primer postulado.
La discusión precedente estaba dirigida al hemisferio izquierdo del cerebro del lector (el de las tareas logicoverbales). Hagamos trabajar ahora al hemisferio derecho (el de las visuales y espaciales). La figura 4 representa el diagrama espaciotemporal del escenario anterior. La línea de universo del astronauta y las del morro y la cola de su nave son las que aparecen inclinadas a la derecha. Tomemos una regla, mantengámosla horizontal y hagamos un barrido desde la parte inferior a la superior del diagrama. Las intersecciones de las líneas de universo con la regla representarán el modo en que la escena tiene lugar desde nuestro punto de vista. Observemos cómo el astronauta y su nave se mueven de izquierda a derecha a medida que movemos lentamente la regla hacia arriba. Los rayos de luz que el astronauta envía hacia el morro y la cola de la nave y luego recibe de vuelta son líneas inclinadas 45 grados, puesto que viajan a 0,3 metros por nanosegundo. La llegada del rayo de luz a la cola de la nave (el suceso A) ocurre, para nosotros, antes que la llegada del rayo de luz al morro (el suceso B). Pero para el astronauta, que se considera en reposo, ambos sucesos son simultáneos y se producen a los 15 nanosegundos de tiempo de la nave, como indican los pequeños relojes y la línea inclinada de trazos (con la etiqueta 15 ns TN, que los une).
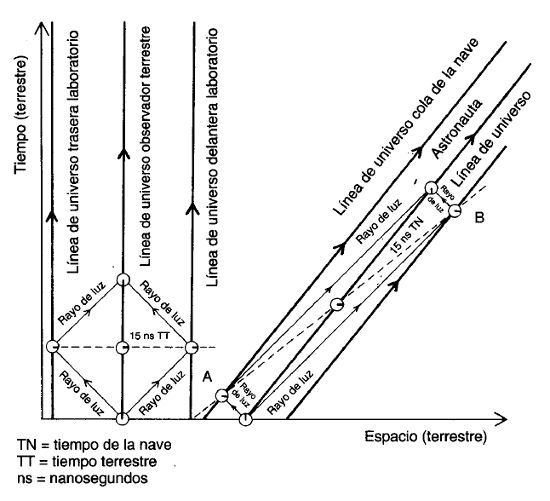
FIGURA 4. Distintas percepciones del tiempo: astronauta y observador terrestre.
En la misma figura se muestra un experimento equivalente, realizado por un observador terrestre. La línea de universo de este observador asciende en vertical, ya que permanece inmóvil respecto a nosotros cuando movemos la regla hacia arriba. La línea que une los relojes terrestres, que representa 15 nanosegundos de tiempo terrestre (y etiquetada como 15 ns TT), es horizontal pues se halla en reposo respecto a nosotros.
El espacio-tiempo es como una barra de pan. Si corto el pan horizontalmente, tendré rodajas que representan diferentes instantes de tiempo terrestre. Dos sucesos serán simultáneos si se hallan en la misma rebanada. Pero un astronauta en movimiento cortará el pan de otra manera, inclinando el cuchillo. Los sucesos que estén en una misma rodaja inclinada serán simultáneos para él. Esto explica también por qué el astronauta y nosotros discrepamos sobre la longitud de la nave. Simplemente estamos cortando su línea de universo tetradimensional de manera diferente. Es como si nos preguntásemos por el grosor de un tronco de árbol. Visto en dirección radial, tendremos una respuesta, pero si lo miramos bajo un cierto ángulo, obtendremos otra.
Es el momento en el que usted puede decidir cuál de sus dos hemisferios predomina. Si es como la mayoría de la gente, prevalecerá su hemisferio izquierdo y encontrará la descripción verbal más convincente que el diagrama espaciotemporal, que suele resultar infrecuente y extraño. Lo he incluido para contentar a los que, como yo, están dominados por el hemisferio derecho. Vi el diagrama por primera vez en un libro de Max Born —Premio Nobel y abuelo de la cantante Olivia Newton-John— cuando estaba en octavo. Fue toda una revelación para mí.
Si un astronauta atravesara el sistema solar al 99,995% de la velocidad de la luz, observaríamos que el ritmo de sus relojes es la centésima parte del de los nuestros y que la longitud de su nave se ve reducida en el mismo factor. Supongamos que se dirige a la estrella Betelgeuse, a unos quinientos años luz de la Tierra. Como viaja casi a la velocidad de la luz, según nuestras cuentas tardaría en llegar algo más de quinientos años, pero como sus relojes avanzan mucho más despacio que los nuestros, le veríamos envejecer sólo cinco años durante el viaje. Cuando llegue a Betelgeuse será sólo cinco años mayor que cuando pasó por aquí.
Pero ¿qué es lo que experimenta el astronauta? Él se considera en reposo. Ve que el Sol y Betelgeuse se mueven respecto a él al 99,995% de la velocidad de la luz, con lo que, al medir la separación entre ambas estrellas, obtiene sólo cinco años luz (la centésima parte de la distancia que medimos nosotros). El Sol y Betelgeuse son como el morro y la cola de una «nave» que pasa junto a él a una velocidad próxima a la de la luz. Al medir su longitud, ésta resulta ser cinco años luz. Es decir, la cola de la «nave» —Betelgeuse— pasa ante él unos cinco años después de haberlo hecho el Sol, con lo que al llegar a su destino es sólo cinco años más viejo, tal como estaba previsto.
Curiosamente, en los experimentos mentales de Einstein no había gente en la Tierra que observara a un astronauta viajando en una nave espacial; en lugar de ello, el gran físico analizaba el caso de un observador situado en una estación de ferrocarril que compara sus anotaciones con otro ubicado en el centro de un tren que se mueve rápidamente. Einstein empleaba un tren porque era el vehículo más rápido de los existentes en 1905.