2
El grande entre los grandes: Isaac Newton

En uno de los ensayos más vibrantes y apasionados que he leído a lo largo de mi vida, el economista John Maynard Keynes (1883-1946) se refería a Isaac Newton —que nació, recordemos, en 1642 y falleció en 1727— como el «último de los magos, el último de los babilonios y de los sumerios; la última de las grandes mentes que contempló el mundo visible e intelectual con los mismos ojos que aquellos que empezaron a construir nuestra heredad intelectual, hace casi diez mil años».

Es evidente que semejante caracterización contiene elementos inaceptables. Newton introdujo en el análisis de los fenómenos naturales —de los físicos especialmente— un método radicalmente nuevo; un método que si ya le distinguía de sus predecesores más cercanos (como Galileo, Kepler o Descartes), más le separaba aún de todos aquellos que habían empezado, milenios antes, a «construir nuestra heredad intelectual». En este sentido, ciertamente no contempló el mundo físico de la misma manera que los antiguos. Y sin embargo, a pesar de tales diferencias, las frases de Keynes —que llegó a reunir una de las colecciones más importantes de manuscritos teológicos newtonianos— contienen algo de verdad y tocan la esencia del pensamiento del catedrático lucasiano de Cambridge. Este elemento de verdad se aprecia con mayor claridad cuando, más adelante en su ensayo, Keynes explicaba los calificativos que había aplicado a Newton:

¿Por qué lo llamo mago? Porque contemplaba el universo y todo lo que en él se contiene como un enigma, como un secreto que podía leerse aplicando el pensamiento puro a cierta evidencia, a ciertos indicios místicos que Dios había diseminado por el mundo para permitir una especie de búsqueda del tesoro filosófico a la hermandad esotérica. Creía que una parte de dichos indicios debía encontrarse en la evidencia de los cielos y en la constitución de los elementos (y esto es lo que erróneamente sugiere que fuera un filósofo experimental natural); y la otra, en ciertos escritos y tradiciones transmitidas por los miembros de una hermandad, en una cadena ininterrumpida desde la original revelación críptica, en Babilonia. Consideraba al universo como un criptograma trazado por el Todopoderoso.

Retrato de Isaac Newton pintado por Godfrey Kneller (1689).

De hecho, Newton dedicó esfuerzos inmensos a la tarea de desvelar semejante criptograma, dejando tras de sí millones de palabras escritas, la mayoría de las cuales ni vieron la luz mientras vivió, ni lo han hecho después. Su esfuerzo fue doblemente intenso en tanto que pensaba que la religión verdadera había sido corrompida por deformaciones e idolatrías introducidas en el pasado; consecuentemente, la religión auténtica, la única que podía proporcionar un conocimiento firme, solamente se podía llegar a conocer sumergiéndose en el mundo de los antiguos.

La búsqueda de aquel conocimiento primordial no contaminado constituyó el gran objetivo de la vida de Newton, dedicándole seguramente más tiempo y esfuerzos que a sus investigaciones científicas, que por otra parte también participaban de sus preocupaciones religiosas. En este aspecto, Newton era un hombre de su tiempo, ya que el camino que había conducido desde el monoteísmo primitivo hacia la idolatría constituía uno de los temas favoritos para los historiadores cristianos de los siglos XVII y XVIII que se ocupaban de las primeras épocas de la humanidad.

He dicho que los intereses religiosos (plasmados en investigaciones en campos como la teología, historia de las religiones o cronología de los reinos antiguos) de Newton no estuvieron al margen de sus preocupaciones científicas. Esto es algo que se puede comprobar de varias maneras. En, por ejemplo, su preocupación por los templos antiguos, y a la cabeza de ellos el Templo de Salomón.

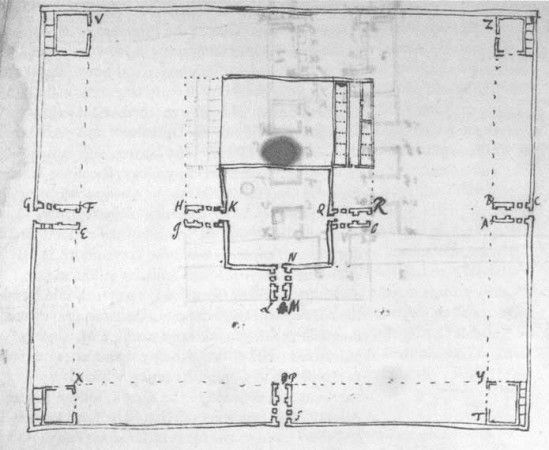
Uno de los seis dibujos debidos a Newton que aparecen en su manuscrito A Treatise or Remarks on Solomon’s Temple, en el que se muestra la planta del templo (Colección Babson, Burndy Library, MIT).

Newton, al igual que tantos otros antes que él, creía que los templos no sólo escondían datos relativos a los modos de adoración al Dios o dioses antiguos, sino que también transmitían información sobre la ciencia, porque, sostenía, los antiguos, además de atesorar la religión verdadera, habían conocido la ciencia auténtica. Al fin y al cabo, leemos en uno de sus manuscritos inéditos, «la primera religión fue más racional que todas las demás hasta que las naciones la corrompieron. Ya que no existe forma… de acceder al conocimiento de una deidad salvo mediante la naturaleza». Esta última frase, «salvo mediante la naturaleza», es, por supuesto, significativa y ayuda a comprender por qué existió un Newton científico. Si pensamos, aunque sea por un momento (no es una idea absurda o infundada), que para él lo más importante era saber algo de Dios y de su obra, aproximarse a él y a ella, y no la física o la matemática, entonces podríamos entender su actividad científica como un medio de acercarse al Todopoderoso.

Las descripciones que en algunos de sus manuscritos hacía del monoteísmo primitivo y de los rituales de adoración después del diluvio, tal y como se practicaban en lugares como Egipto, Babilonia o Caldea, identificaban estrechamente la primera ciencia con la teología. Los sacerdotes y líderes religiosos de aquellas antiguas civilizaciones también fueron, argumentaba, sus científicos y filósofos. La astronomía había comenzado entre los sacerdotes egipcios y caldeos, que al decorar sus templos habían hecho de ellos réplicas exactas del universo. De hecho, atribuía a los antiguos el conocimiento del heliocentrismo copernicano. Los rituales religiosos escondían significados científicos: el movimiento de las procesiones de sacerdotes entre los egipcios, por ejemplo, demostraba que su teología estaba basada en la ciencia de las estrellas; de manera análoga, cuando los sacerdotes judíos se aproximaban al altar, daban vueltas alrededor del fuego, encendiendo siete lámparas para representar los planetas que se mueven en torno al Sol (Mercurio, Venus, la Tierra, Marte, Júpiter, Saturno y la Luna, considerada también como un planeta).

El interés de Newton por los conocimientos científicos que pudieron atesorar los antiguos llegó al extremo de que en algún momento planeó incluir al principio del Libro III de su obra magna, los Principia, a la que me referiré más adelante, una serie de escolios (especie de comentarios finales) con referencias a esa supuesta sabiduría antigua, retrotrayéndose no sólo hasta figuras históricas como Tales y Pitágoras, sino incluso hasta sabios míticos de la antigüedad. Finalmente no lo hizo, pero en la Óptica, su otro gran libro junto a los Principia, sí que es posible encontrar rastros de su interés por los antiguos. En la «Cuestión 20» de la edición latina de 1706 («Cuestión 28» a partir de la edición inglesa de 1717), cuando atacaba la idea de la existencia de un medio, «tan denso como el agua», en el cielo, afirmaba: «Para el rechazo de tal medio, disponemos de la autoridad de aquellos de los más ancianos y célebres filósofos de Grecia y Fenicia, quienes hicieron del vacío, los átomos y la gravedad de los átomos los primeros principios de su filosofía, atribuyendo tácitamente la gravedad a una causa distinta de la materia densa. Filósofos posteriores borraron de la filosofía natural la consideración de tal causa, imaginando hipótesis para explicar mecánicamente todas las cosas y relegando a la metafísica todas las demás causas».

De hecho, ni siquiera los Principia están libres del Newton teólogo. En la segunda edición —publicada en 1713, cuando tenía setenta y un años—, decidió cerrar su gran monografía con unas páginas dedicadas a la divinidad. Se trata del célebre «Escolio General», en el que pretendía poco menos que definir a Dios:

Es eterno e infinito, omnipotente y omnisciente; esto es, dura desde la eternidad hasta la eternidad y está presente desde el infinito hasta el infinito: lo rige todo; lo conoce todo, lo que sucede y lo que puede suceder. No es la eternidad y la infinitud, sino eterno e infinito; no es la duración y el espacio, sino que dura y está presente. Dura siempre y está presente en todo lugar, y existiendo siempre y en todo lugar, constituye la duración y el espacio.

En ese mismo «Escolio» también es posible adivinar algo que el propio Newton se esforzó por ocultar durante toda su vida: que era un hereje arriano, que su Dios no era trino, sino uno: «Dios —escribió allí— es uno y el mismo dios siempre y en todo lugar».

¿Por qué un Newton oculto?

Newton fue, efectivamente, un hereje. Pensaba que el texto griego del Nuevo Testamento estaba gravemente contaminado por los trinitarios y que era preciso recuperar sus manifestaciones originales, en las que Jesús no era consustancial o coeterno con Dios. Creía, como ya he dicho, que Dios era uno y no trino. El que se hubiese perdido la creencia en un único y todopoderoso Dios había sido debido, argumentaba, muy especialmente a san Atanasio (296-373). Éste había asistido siendo muy joven al Concilio de Nicea de 325, en el que, tras un largo y áspero debate, se aprobó la doctrina conocida como homoousion (homousismo), que sostiene que Cristo es de la misma sustancia que el Padre. En el año 328, Atanasio fue nombrado obispo de Alejandría, empleando el resto de su vida en defender aquel dogma y en combatir a los arrianos, esto es, a los seguidores de Arrio (260-336), que había sostenido que Cristo, creado y no eterno, estaba subordinado a Dios.

Anotaciones de Newton enumerando los «Seven precepts of the Noachides» al final de su ejemplar de la Opticks (edición de 1717, Colección Babson, Burndy Library, MIT).

Atanasio se convirtió en la gran bestia negra de Newton, quien planeó escribir una obra en la que pondría al descubierto sus engaños, al igual que las atrocidades que suponía había cometido (incluyendo el asesinato del arzobispo Arsenio). De este tratado, que nunca llegó a completar, nos han llegado varios borradores, con el título de Paradoxical Questions concerning ye morals and actions of Athanasius and his followers (Cuestiones paradójicas relativas a las morales y acciones de Atanasio y de sus seguidores). En la soledad de su estudio de Cambridge, la pasión e indignación del autor de los Principia contra Atanasio y la Iglesia de Roma se desbordaba: «Idólatras… blasfemos, y fornicadores espirituales», son algunos de los adjetivos que utilizaba.

Sin embargo, y a pesar de la vehemencia que en privado ponía en sus ataques al trinitarismo y defensa de Arrio, Newton mantuvo secreta su opinión de que las Escrituras habían sido corrompidas. Pocos accedieron a este mundo histórico-teológico newtoniano. El motivo es muy sencillo: los estatutos de su college, Trinity (más concretamente, Holy and Undivided Trinity: Sagrada e Individida Trinidad), obligaban a sus miembros a ser ordenados clérigos de la Iglesia anglicana dentro de los siete años posteriores a la recepción del grado de master of arts, o enfrentarse a la expulsión; asimismo, los estatutos de su cátedra indicaban que las opiniones heréticas constituían motivo de expulsión.

El que no aceptase el dogma trinitario le ponía, por tanto, en una situación muy difícil. No aceptaba una creencia central de la Iglesia a la que se suponía pertenecía y no podía fingir. Se trataba de algo vital, iba en ello su salvación eterna. Él creía en Dios; en un Dios, además, absoluto e imponente. Un Dios que, probablemente, no perdonaría a aquel que, sabiendo, engañaba.

Finalmente, en el último momento, el problema desapareció. Una dispensa real promulgada el 27 de abril de 1675 libraba para siempre al ocupante de la cátedra lucasiana —y por tanto a Newton— de cualquier requisito colegial de ordenación. No sabemos de quién partió la iniciativa para lograr esa dispensa. Tal vez fuese de Isaac Barrow (1630-1677), su predecesor en la cátedra lucasiana, entonces master del Trinity College y una persona con influencia ante el rey. En cualquier caso, lo seguro es que Newton pudo así mantener sus opiniones religiosas en secreto.

Un hombre de su tiempo

Antes de abandonar definitivamente este ámbito, tan poco frecuentado cuando se habla de Newton, el gran héroe científico, y por tanto de la Racionalidad, que, parece, tiene que estar al margen de creencias y pasiones más mundanas; antes, digo, de abandonar este ámbito, señalaré que no se debe pensar que en lo que se refiere a su interés por la teología —no en lo referente a sus ideas heréticas—, Newton fue un científico, un filósofo natural, raro en su tiempo. De Isaac Barrow, su primer biógrafo dijo: «Temía, como clérigo, emplear demasiado tiempo en las Matemáticas, ya que… en su ordenación había jurado servir a Dios en el Evangelio de su Hijo, y no podía hacer una Biblia de su Euclides, o un púlpito de su cátedra matemática». De hecho, su renuncia a la cátedra lucasiana puede entenderse como un acto destinado a romper con las obligaciones científicas que le imponía su puesto académico, para así poder dedicarse con mayor libertad al estudio del Libro de la Palabra de Dios.

, Robert Boyle (1627-1691), retratado hacia 1689 por Johann Kerseboom.

Especialmente interesante es el caso del químico y físico Robert Boyle (1627-1691), uno de los grandes exponentes de la filosofía experimental inglesa, así como uno de los pilares de la Royal Society, que también fue un prolífico autor sobre temas de teología natural, el lugar en el que ciencia y religión se encontraban. Eso sí, Boyle no padeció remordimientos de conciencia al estilo de Barrow por su dedicación a la filosofía natural (esto es, a la ciencia). Además, estaba convencido de que un Dios que podía crear un universo mecánico, al igual que materia en movimiento que obedecía ciertas leyes universales, era más admirable que un Dios que crease un universo sin leyes científicas.

No es difícil encontrar más ejemplos de esfuerzos parecidos a los de Boyle de poner en evidencia la armonía entre ciencia y religión. Basta con ojear libros como The Wisdom of God Manifested in the Works of Creation (La sabiduría de Dios manifestada en las obras de la creación; 1691), de John Ray (1627-1705), el principal naturalista de la época, o Astronomical Principles of Religion, Natural and Revealed (Principios astronómicos de religión, natural y revelada; 1717), de William Whiston (1667-1752), el sucesor de Newton en la cátedra lucasiana, y creyente como él en las ideas antitrinitarias del hereje Arrio.

Pero la casuística es muy amplia, y ya es hora de dirigirse hacia Newton el científico, el Grande entre los Grandes de la ciencia.

Vesalio, Copérnico y la Revolución Científica

No es posible, sin embargo, hablar de él en tal categoría sin referirse antes a un momento especialmente singular en la historia de la ciencia: la Revolución Científica, el período de los siglos XVI y XVII, durante el cual se establecieron los fundamentos conceptuales e institucionales de la ciencia moderna.

Aunque las fechas concretas son como la punta de un iceberg, que oculta un largo período de incubación, un buen punto de partida es 1543, cuando se publicaron dos libros que terminarían convirtiéndose en clásicos de la historia de la ciencia: De humani corporis fabrica (La fábrica del cuerpo humano), de Andreas Vesalio (1514-1564), y De revolutionibus orbium coelestium (Sobre las revoluciones de los orbes celestes), de Nicolás Copérnico (1473-1543).

A pesar de que ninguno de los dos logró superar completamente la herencia recibida (Vesalio no supo desembarazarse de aspectos importantes de la anatomía y medicina galénica, del mismo modo que Copérnico no logró apartarse del sistema de los círculos perfectos para los movimientos de los cuerpos celestes), se puede decir que ambos libros fueron revolucionarios, o, cuando menos, que constituyeron los cimientos de futuros cambios revolucionarios, en la anatomía y en la astronomía y mecánica, respectivamente; que inspiraron una serie de actividades, ideas y desarrollos que conducirían en el plazo de un par de generaciones a la promulgación de conceptos y teorías ya muy distintas a las antiguas.

La fábrica del cuerpo humano constituyó un vibrante llamamiento en defensa de la práctica anatómica, de la disección, como base imprescindible para la comprensión de la estructura y funciones del cuerpo humano. Basta, en este sentido, con leer algunos pasajes de la «Dedicatoria a Carlos V, el más grande e invicto emperador», que Vesalio incluyó en su obra:

Mientras los médicos afirmaban que sólo les incumbía la curación de las afecciones internas, pensando que les bastaba con conocer las vísceras, se desentendieron de la estructura de los huesos, los músculos, los nervios, las venas y las arterias que se extienden por los huesos y los músculos, como si no fuera cosa suya. Además, como se confiaba a los barberos toda la disección, los médicos no sólo perdieron el conocimiento auténtico de las vísceras, sino que también desapareció completamente la actividad de la disección, porque éstos no se ocupaban de hacer disecciones; a su vez, aquellos en cuyas manos se dejaba esa actividad eran tan ignorantes que no entendían los escritos de los maestros de disección. Sólo faltaba que esta clase de hombres conservaran para nosotros este arte dificilísimo, que les fue transmitido a ellos de manera práctica, y que esta deplorable dispersión de la parte curativa nos introdujera en las escuelas la deplorable costumbre según la cual unos se acostumbraron a diseccionar el cuerpo humano y otros a describir sus partes. Éstos, a modo de grajos, hablan a gritos y con gran boato desde su cátedra de lo que nunca han practicado y que sólo recuerdan por libros ajenos o de los dibujos que ponen delante de sus ojos; a su vez, los primeros desconocen las lenguas en tal medida que no pueden explicar las disecciones a los espectadores y despedazan lo que debe mostrarse según la prescripción del físico, el cual, sin aplicar nunca sus manos a la disección, sólo enseña comentando con altivez. Y del mismo modo que enseñan todo al revés y pierden días enteros en cuestiones ridículas, de igual manera en medio de esa algarabía plantean a los espectadores menos cuestiones de las que un carnicero puede enseñar a un médico en el matadero, por no decir nada de esas escuelas donde apenas se reflexiona sobre la disección de las articulaciones del cuerpo humano. ¡Hasta tal punto la vieja medicina se ha apartado desde hace muchos años del antiguo esplendor!

Vesalio según De humani corporis fabrica (1543). Cuando se hizo el retrato (1542) tenía veintiocho años.

Portada de la segunda edición (Basilea, 1555) de De humani corporis fabrica de Vesalio.

Básicamente, durante casi trescientos años, siguiendo el programa defendido en La fábrica del cuerpo humano, todo examen del funcionamiento de los organismos vivos se fundó en la anatomía, mejorando sustancialmente el alcance y precisión del conocimiento relativo a la estructura del cuerpo humano, conocimiento en el que se basarían algunos científicos para dar pasos de tal calibre como el realizado por William Harvey (1578-1657) al descubrir la circulación mayor de la sangre (1628). Fue entonces, y sólo entonces, con Harvey, cuando realmente surgieron conflictos serios entre las ideas médicas antiguas y modernas. Más aún, con Harvey —y en cierta medida también a través de las teorías de Descartes— se produjo la primera de las revoluciones que se han producido en la biología: la introducción de la biología mecánica, que no se desarrollaría completamente hasta más de dos siglos después.

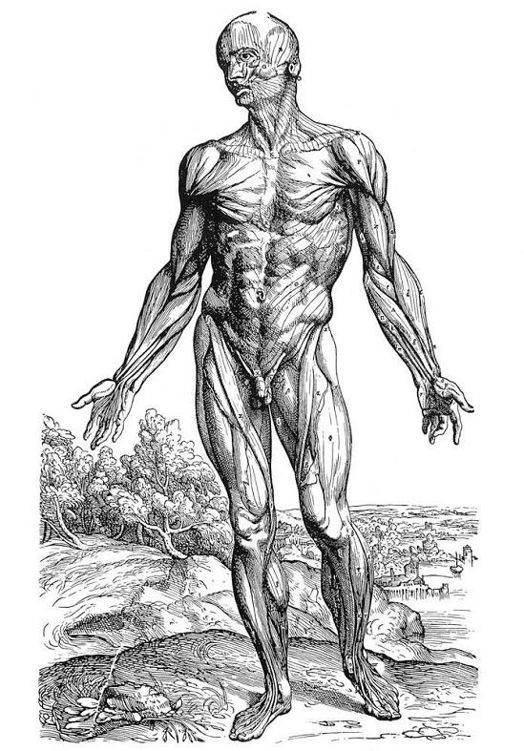
Lámina de De humani corporis fabrica.

Mientras que La fábrica era, fundamentalmente, un texto de carácter experimental y programático, Sobre las revoluciones de los orbes celestes se puede considerar como una obra de filosofía natural y, sobre todo, de matemática aplicada, que no incluía observaciones astronómicas nuevas, ni aspiraba a que sus predicciones fueran de una exactitud sin precedentes. Lo que hizo Copérnico fue recuperar una vieja idea (ya había sido utilizada por uno de los grandes astrónomos griegos, Aristarco de Samos [c. 310-230 a.C.], en cuyo haber se encuentran resultados como el haber identificado la oblicuidad de la eclíptica, el plano que forma la Tierra al girar en torno al Sol; asimismo, en una obra cuya versión latina se publicó por primera vez en 1572, De magnitudinibus, la única que nos ha llegado de él, analizó el tamaño del Sol y de la Luna, estimando las distancias entre sí y con respecto a la Tierra): la de que es el Sol y no la Tierra el que se encuentra, inmóvil, en el centro del universo. Una idea que no pudo imponerse, dentro de la tradición astronómica helena, al sistema geocéntrico (la Tierra está en el centro del universo), que culminó en una obra de Claudio Ptolomeo, «Ptolomeo de Alejandría», en la que se resumieron siglos de astronomía griega, conocida por su nombre árabe, Almagesto («el más grande»).

Retrato de Copérnico, siglo XVII, anónimo (Biblioteca Universitaria de Bolonia).

Pero la adopción del sistema heliocéntrico que propugnaba Copérnico frente a la visión cosmogónica en la que la Tierra ocupaba el centro del universo, y a la que tan estrechamente ligada estaba la física que desarrolló Aristóteles y que insertó profundamente en todo su sistema científico-filosófico, presentaba problemas. De no haber sido por Johannes Kepler (1571-1630) y Galileo Galilei (1564-1642), el sistema copernicano seguramente habría contribuido a perpetuar el que Ptolomeo inmortalizó, aunque en una forma un poco más compleja pero más grata para algunos.

Antes, sin embargo, de pasar a Kepler y Galileo, es inevitable, a la vista de todo lo que se ha escrito sobre el tema, considerar la siguiente pregunta: ¿creía el propio Copérnico en el sistema del mundo que proponía en De revolutionibus?, ¿pensaba, efectivamente, que la Tierra gira en torno al Sol, o lo consideraba como un mero artificio?

La conveniencia de plantearse tales cuestiones, en lugar de pensar, simplemente, que por qué no habría de creer en el heliocentrismo, tiene que ver con la actitud reinante entonces en la poderosa Iglesia católica, que favorecía firmemente el sistema aristotélico-ptolemaico, un sistema en el que, repito, la Tierra se encuentra en el centro del universo, visión que se acomodaba bastante bien con la idea cristiana de que los seres humanos (la única criatura creada, según esa religión, a imagen de Dios) constituyen la obra favorita, central, de Dios. Y no hay que olvidar el clima reinante entonces dentro de la Iglesia, clima que culminó en el Concilio de Trento (1546), cuando se decretó, dentro del contexto de la lucha contra la Reforma, que al interpretar la Biblia no había que desviarse de las doctrinas mantenidas por los Padres de la Iglesia; en particular que la Biblia también era una fuente de datos científicos y que cualquier afirmación contenida en ella debía tomarse como científicamente verdadera.

Página del manuscrito autógrafo de Copérnico de De revolutionibus orbium cœlestium, conservado en la Biblioteca Jagielloniana de Cracovia.

A la vista de lo que Copérnico escribió en su, literariamente abigarrado, «Prefacio» a De revolutionibus, parece que el astrónomo y sacerdote polaco creía en la verdad del sistema heliocéntrico. Resulta, no obstante, que la lectura de De revolutionibus quedó condicionada por el contenido de otro «Prefacio» incluido en la obra, que, además, precedía al de Copérnico. Este «Prefacio» apareció en la primera edición sin firmar, pero no fue debido a Copérnico sino a la pluma del teólogo protestante Andreas Osiander (1498-1552), responsable de la edición de la obra, quien lo incluyó, según sabemos, sin que Copérnico, que de hecho murió —el 24 de mayo de 1543— mientras se imprimía su libro, lo autorizase (no se sabe si llegó a ver, en su lecho de muerte, un ejemplar). La opinión que sostenía allí Osiander —«no espere nadie», escribía, «en lo que respecta a las hipótesis, algo cierto de la astronomía, pues no puede proporcionarlo»— no apoyaba que fuese verdad el sistema heliocéntrico, y, al aparecer sin firmar, fue tomada, inevitablemente, como el punto de vista del propio autor del libro.

Tal vez por esto De revolutionibus tuvo a la postre menos problemas con la Iglesia de Roma —aunque también los terminó teniendo— que otros libros: en 1616, más de 70 años después de su publicación, fue incorporado al Index Librorum Prohibitorum, pero quedó proscrito «donec corrigatur» («hasta que sea corregido»), mientras que el Diálogo sobre los dos máximos sistemas del mundo de Galileo, prohibido en 1633, ingresó en el Index incondicionalmente, y ahí siguió hasta 1835, a pesar de que en 1757 el papa Benedicto XIV había revocado el decreto anti-copernicano.

Kepler y Galileo

Como apunté antes, fueron Kepler y Galileo quienes avanzaron sustancialmente en la dirección de desarrollar una astronomía y una «ciencia del movimiento» que diesen sentido al sistema heliocéntrico, ya que Copérnico no desarrolló una dinámica que hiciera plausible la idea de una Tierra que no se encontraba en reposo: si esto fuese así, si la Tierra estuviera, efectivamente, en movimiento ¿cómo es que los objetos libres no se alejaban de la superficie terrestre?, ¿por qué no se veía que las nubes siempre se dirigían hacia el oeste y los cuerpos arrojados desde una torre no caían al oeste de la base de la misma? Había, en definitiva, que crear una física en la que tuviese cabida la noción de sistemas que mantenían su estado de movimiento si no se les sometía a algún tipo de influencia externa, algo que llevarían a cabo sobre todo Descartes y Newton, con la denominada ley de la inercia, a la que se acercó Galileo, aunque el de Pisa no fuese capaz de abstraer la presencia de la fuerza de la gravedad (para él, un cuerpo dejado libremente sobre, por ejemplo, la superficie de la Tierra tendría como movimiento natural el circular, el correspondiente a la superficie del planeta productor de gravedad; por el contrario, lo que Descartes y Newton dirían es que un cuerpo realmente libre lo es también de la fuerza gravitacional, con lo cual su movimiento es una trayectoria rectilínea, no circular).

A pesar de todo lo que aportaron científicos como Galileo (recordemos en este sentido su gran libro, Discorsi e dimostrazioni matematiche, intorno à due nuove scienze attenenti alla mecanica i movimenti locali [Discursos y demostraciones matemáticas en torno a dos nuevas ciencias que se ocupan de la mecánica y de los movimientos locales], publicado en 1638), no hay que pensar que la «ciencia del movimiento» fue creada en los siglos XVI y XVII. Aristóteles, autor de libros como la Física, viene enseguida a la mente: fue, en efecto, un estudioso del movimiento, por mucho que las soluciones que dio puedan parecer a muchos tan contaminadas por planteamientos filosóficos que cometan el error de considerarlas «pura metafísica» (en el peor sentido de este otrora noble término). Más acorde, en cualquier caso, con los esquemas que finalmente se impusieron en esa ciencia del movimiento (más concretamente, en el caso de la dinámica de los fluidos) fueron algunos trabajos de otro nombre mítico de la ciencia griega: Arquímedes (c. 287-212 a.C.).

Hijo de un astrónomo, Fidias, tras estudiar en Alejandría, Arquímedes regresó a su ciudad natal, Siracusa (Sicilia), de cuyo rey, Hierón II, era pariente. Sus habilidades tecnológicas (entre sus inventos se encuentra el denominado «tornillo de Arquímedes», un tornillo espiral que se hacía girar dentro de un cilindro y que se podía utilizar para sacar agua de los canales) fueron aprovechadas durante el asedio romano a Siracusa (215-212 a.C.), en el que, según algunos cronistas, inventó una serie de armas e instrumentos que mantuvieron alejada a la flota romana, al provocar incendios en algunos de sus barcos. Según la leyenda, murió en el subsiguiente saqueo de Siracusa, asesinado por un soldado romano, que no fue capaz de hacerle salir de su estudio, inmerso como estaba en sus investigaciones.

Fue también un maestro en las artes matemáticas, logrando con ellas algo que otros ni siquiera se plantearon: aplicar la maestría matemática de los griegos a la investigación de fenómenos naturales tan aparentemente, sólo aparentemente, nimios, como el comportamiento de un sólido en un fluido. Suyo es el denominado «principio de Arquímedes», que afirma que un cuerpo sumergido en un fluido experimenta un empuje igual al peso del volumen del fluido que desaloja, y cuya demostración incluyó en dos proposiciones de uno de sus libros: Sobre los cuerpos flotantes.

Regresando ahora al ámbito, no por más materialmente distante menos atractivo, de los movimientos de los cuerpos celestes, hay que detenerse en el ya citado Johannes Kepler. Ahora bien, es imposible comprender la obra de éste sin recordar, a su vez, al gran astrónomo danés Tycho Brahe (1546-1601).

Brahe fue uno de los más grandes observadores astronómicos de todos los tiempos, sin duda de aquellos anteriores a la introducción del telescopio, superando en la precisión de sus medidas a todos sus predecesores. Apoyado por el rey Federico II (el propio Tycho era noble), pudo construir un gran centro astronómico —Uraninburgo— en la isla de Hven, en el estrecho de Sund, que separa Dinamarca y Suecia, dotado de todos los recursos disponibles en su época para la observación de los movimientos de los cuerpos celestes, entre ellos, en una sala de la planta baja, un enorme cuadrante mural para medir la altitud a la que tales cuerpos cruzaban el meridiano, dentro del cual, como adorno, estaba pintado, a tamaño natural, el propio Brahe sentado.

Para acomodar los resultados que obtuvo (muchos de los cuales —entre ellos el descubrimiento, en 1572, de una supernova, la «estrella de Tycho», que apareció repentinamente en la constelación de Casiopea, y que llegó a superar el brillo de Venus, siendo visible en pleno día— incluyó en su gran libro: Astronomiae instauratae mechanica [Instru men tos para la restauración de la astronomía], cuya edición definitiva vio la luz en 1602), Tycho propuso un modelo a medio camino entre el geocéntrico y el heliocéntrico; uno en el que los planetas giraban en torno al Sol, aunque éste, a su vez, lo hacía alrededor de la Tierra, todavía inmóvil en el centro del universo. En 1599, en una decisión en la que tuvieron que ver problemas que surgieron entre el astrónomo y su rey, Brahe abandonó Dinamarca, instalándose en Praga, como astrónomo y matemático de Rodolfo II, aunque no pudo disfrutar mucho de su nuevo puesto, ya que falleció poco tiempo después.

Como sucesor suyo fue designado uno de sus ayudantes en Praga, Kepler, quien enseguida se sumergió en el estudio de la órbita de Marte, apoyándose en el tesoro que constituían los datos acumulados a lo largo de los años por Brahe. Así, en 1609 publicaba un libro, Astronomia nova (Nueva astronomía), en el que presentaba sus dos primeras leyes del movimiento planetario, descubiertas tras una ardua tarea en la que indudablemente debió desempeñar un papel importante la realización de interminables cálculos para intentar ajustar a alguna trayectoria los datos de que disponía. Y resultó que las órbitas que mejor se amoldaban a tales datos eran las elípticas, elipses en uno de cuyos focos estaba el Sol (primera ley de Kepler) y no la Tierra, un hecho que evidentemente favorecía las tesis copernicanas, de las que Kepler fue un ferviente admirador. En cuanto a la segunda ley (la de las áreas: el vector radial describe áreas iguales en tiempos iguales), servía para describir la velocidad con que los planetas se movían a lo largo de esas elipses. Y aún formularía —en Harmonices mundi (1619)— una tercera ley, que relacionaba períodos de revolución y distancias al Sol. Merece la pena también señalar que Kepler fue uno de los primeros astrónomos que se benefició en algunos de sus cálculos de la reciente invención de los logaritmos, que el matemático escocés John Napier (1550-1617) difundió especialmente en su libro Mirifici logarithmorum canonis descriptio, 1614 (Descripción de la maravillosa regla de los logaritmos). Y es que la ciencia, y en particular la astronomía y la física, depende para su avance de los elementos matemáticos de que se dispone en cada momento; hoy son los poderosos ordenadores, mientras que en tiempos de Kepler, fueron los logaritmos.

Retrato de Tycho Brahe en Astronomiae instauratæ mechanica (1602).

El gran mural astronómico, pintado en el observatorio de Uraniburgo, para medir las altitudes a las que los cuerpos celestes cruzaban el meridiano. En él aparece Tycho Brahe. Lámina de Astronomiae instauratæ mechanica (1602).

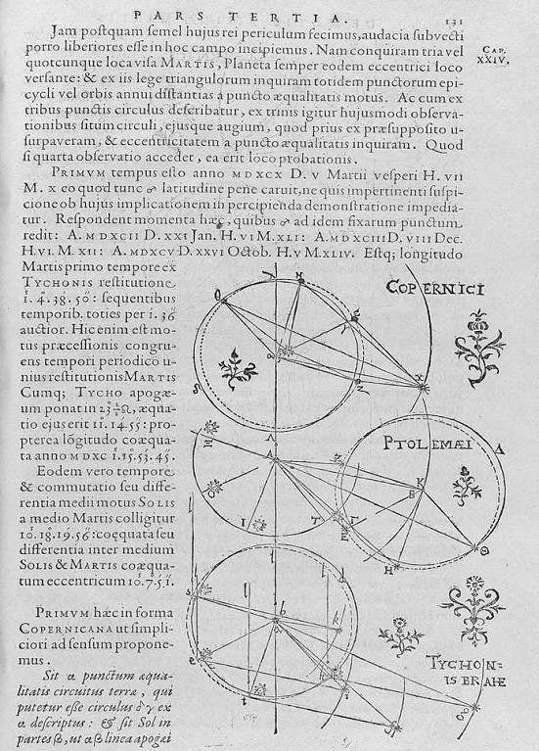
Lámina de Astronomia nova (Heidelberg, 1609) de J. Kepler, mostrando una misma situación astronómica según los sistemas de Copérnico, Ptolomeo y Brahe.

Retrato de Johannes Kepler, anónimo.

Y así llegamos a Galileo Galilei, con quien la fuerza de las ideas copernicanas se hizo tan patente, que terminaría desencadenando acontecimientos sociales que arrastrarían con ellos al físico pisano. Ello fue la consecuencia inesperada de una serie de observaciones que llevó a cabo y que sacaron a la luz las deficiencias del universo aristotélico-ptolemaico. El que Galileo realizara tales observaciones fue, en principio, sorprendente, ya que era un físico, más preocupado por el estudio del movimiento, por encontrar las leyes que regían fenómenos como la caída de un cuerpo esférico por un plano inclinado o el tiempo que tarda un péndulo en batir, y no un astrónomo. Sin embargo todo cambió, su vida y a la postre, en más de un sentido, el mundo, cuando supo de la existencia de lentes (telescopios refractores) que agrandaban las imágenes de objetos lejanos.

Al oír de la existencia de tales instrumentos (parece que durante una visita que realizó a Venecia en julio de 1609), Galileo decidió construir uno él mismo. Al principio, pensó en él como un aparato cuya utilidad era más práctica que científica —«este instrumento», escribía el 24 de agosto de 1609 a Leonardo Donato, duque de Venecia, «acerca hasta tal punto al ojo los objetos visibles y los representa tan claros y distintos que si un objeto se encuentra, por ejemplo, a nueve millas de distancia, aparece como si sólo estuviera alejado una milla, lo que en todo negocio o empresa marítima o terrestre puede ser de un provecho inestimable»—, pero no tardó en dirigirlo hacia el cielo, viendo que el universo era muy diferente a la armonía de los cinco elementos (cuatro —aire, fuego, tierra y agua— imperfectos, y uno —el éter, la quintaesencia— perfecto), organizados en dos capas, la del mundo sublunar y la del supralunar, mundano y contingente aquél, inmutable y esféricamente perfecto éste, que imaginaban los aristotélico-ptolemaicos.

Con un tosco telescopio de pocos aumentos que él mismo construyó, observó —en noviembre de 1609— la Luna y en su superficie contempló la misma desigual geografía que existía en la Tierra. Vio manchas, que interpretó, correctamente, como producidas por las sombras de «las crestas de las montañas y los abismos de los valles» (Sidereus nuncius [El mensajero sideral]; 1610). El mundo supralunar no se distinguía, por tanto, del terrestre, una conclusión esta que sus posteriores observaciones de Júpiter, en enero de 1610, confirmaron: en las proximidades de este planeta detectó cuatro satélites —«planetas medíceos», los bautizó, buscando favores de los Medici—, que ofrecían una versión en miniatura del universo copernicano; los satélites orbitaban en torno a Júpiter, mientras que el sistema aristotélico-ptolemaico sólo admitía revoluciones alrededor de una estática Tierra. Desaparecía de esta manera uno de los obstáculos que se erigían ante la tesis que Copérnico había defendido.

Portada de Johannes Kepler, Tabulae Rudolphinae (1627), en la que se ve a Hiparco, Copérnico, Brahe y Ptolomeo.

Portada de Machina coelestis pars prior (1673-1679) de Johannes Hevelius (1611-1687), en la que aparecen Hiparco y Ptolomeo junto a Copérnico y Brahe.

Aquellas observaciones —y otras, como la detección de manchas solares— dieron a Galileo una extraordinaria notoriedad en el pequeño mundo de los astrónomos y filósofos de la naturaleza de su época, notoriedad que se afianzó cuando publicó en 1632 un libro inmortal, Dialogo sopra i due massimi sistemi del mondo Tolemaico, e Copernicano (Diálogo sobre los dos máximos sistemas del mundo, ptolemaico y copernicano), una obra maestra de la literatura científica, escrita en lengua vernácula, el italiano, en una época en la que el latín era el idioma utilizado en este tipo de textos. Los tres personajes creados por Galileo para protagonizar ese diálogo (también aparecen en el ya citado Discorsi e dimostrazioni matematiche, intorno à due nuove scienze), Salviati, Sagredo y Simplicio, copernicano el primero, neutral el segundo y aristotélico el último, han pasado a formar parte de la cultura universal, de la misma manera que lo han hecho otros personajes de ficción, como pueden ser, por ejemplo, don Quijote y Sancho Panza. Lo mismo que ha pasado a la memoria colectiva el recuerdo de los problemas que tuvo con la Iglesia católica, las condenas que ésta dictó, primero en 1616 y luego, mucho más firme, en 1633. «Eppur si muove» («Y sin embargo se mueve»), dicen que murmuró cuando se vio obligado, ante el Tribunal de la Inquisición reunido en Roma, el 22 de junio de 1633, a admitir que la Tierra no se movía, a abjurar de sus convicciones copernicanas. Aun suponiendo que fuese así, triste consuelo sería; lo único cierto es que fue humillado, la verdad científica escarnecida, y Galileo confinado hasta su muerte en una villa que poseía en Arcetri.

Los descubrimientos, observaciones y desarrollos teóricos realizados por Galileo, junto con los producidos por Kepler y las contribuciones de Descartes, a quien se debe la ley de la inercia (la primera ley del movimiento en la mecánica clásica), allanaron el camino para la obra de Isaac Newton. Ahora bien, a pesar del trascendental papel desempeñado por estos y otros científicos, constituiría un profundo error olvidar otros factores que también contribuyeron a que pudiese existir la ciencia newtoniana, factores que forman parte esencial de la Revolución Científica. Me estoy refiriendo a la aparición de nuevas instituciones que promovieron la investigación científica.

El asociacionismo científico

Las ideas (experimentos, conceptos y teorías) científicas pueden surgir en ocasiones en escenarios solitarios: Newton llevó a cabo una gran parte de su obra científica con los limitados recursos que poseía en sus habitaciones del Trinity College de Cambridge, aunque, por supuesto, necesitó conocer lo que otros científicos habían descubierto. Pero, tomada en su conjunto, la actividad científica requiere —tanto más cuanto más desarrollada y profesionalizada está— de instituciones en las que los científicos reciban educación especializada, realicen sus experimentos, intercambien ideas y publiquen sus trabajos. También en este sentido la época de la Revolución Científica fue singular, ya que en ella se crearon instituciones como las primeras sociedades científicas realmente significativas y estables.

Retrato de Galileo incluido en Il saggiatore (Roma, 1623).

Portada de Dialogo sopra i due massimi sistemi del mondo Tolemaico e Copernicano (Florencia, 1632) de Galileo.

En la Europa del siglo XVI comenzaron a proliferar las universidades. Podemos hablar de ellas, y con razón, como centros de saber. Pero es esta una denominación un tanto equívoca, ya que las universidades eran entonces, sobre y por encima de todo, centros de enseñanza y, de hecho, sus planes de estudios y división en facultades se mantuvieron estáticos durante siglos. Se necesitaba otro tipo de instituciones para que la ciencia pudiera desarrollarse verdaderamente: las academias y sociedades científicas. Y fue en Italia donde comenzaron a surgir.

Retrato de Galileo Galilei debido a Justus Sustermans (1597-1681), siglo XVII (Florencia, Galería de los Uffizi).

Dibujos de Galileo sobre la Luna, mostrando los perfiles y sombras que observó. Galileo, Sidereus nuncius (Venecia, 1610).

La primera academia que podríamos denominar moderna fue la Accademia dei Lincei de Roma (1603-1630), fundada por el duque Frederico Cesi, un hábil experimentador, especialmente interesado en el estudio de las abejas y las plantas, aficionado a coleccionar objetos naturales y que poseía un jardín botánico. Asimismo, es obligado recordar a la Accademia del Cimento de Florencia (1657-1667) —Cimento significa «experimento» (el lema de la Academia era «Provando e riprovando»)—, en la que nueve científicos (la mayor parte discípulos de Galileo, como Evangelista Torricelli [1608-1647] o Giovanni Borelli [1608-1678]) se esforzaron durante una década en construir instrumentos, desarrollar sus habilidades experimentales y buscar leyes que expresasen el comportamiento de la naturaleza. Estas academias precedieron a otras cuyas actividades y trascendencia serían mucho mayores. Como la Royal Society de Londres (fundada en 1660), que llegaría a presidir el propio Newton, la Académie Royale des Sciences de París (1666), o la Academia de Berlín, fundada por Leibniz en 1700.

Grabado realizado en 1773 por G. Vascellini (Serie di ritratti d’uomini illustri toscani) representando una reunión de la Accademia del Cimento. Nótese el lema de la Academia inscrito en la pared: «Provando e riprovando».

Las academias, esas academias en concreto, proporcionaban un medio de comunicación entre científicos, algo necesario para el progreso de la ciencia, pero hacía falta más. Una limitación importante de estas corporaciones era su reducido ámbito de influencia: una ciudad, la mayor parte de las veces; Londres para la Royal Society, París para la Académie des Sciences, aunque es cierto que su influencia se expandía, individualmente, mucho más allá. El establecimiento de sistemas postales estables (en Inglaterra existió desde comienzos del siglo XVI un servicio postal para las cartas de Estado, pero hasta mediados del siglo siguiente no se creó una oficina postal general para la correspondencia privada) representó una ayuda considerable, ya que el intercambio epistolar entre los científicos constituyó un medio de comunicación muy importante, como muestra la voluminosa correspondencia de científicos e informadores casi profesionales como John Wallis, Robert Boyle, Christiaan Huygens (1629-1695), Marin Mersenne (1588-1648) y Henry Oldenburg (1615-1577), el secretario de la Royal Society que convirtió la correspondencia científica en un arte.

Otro medio de comunicación y difusión científica, desarrollado durante la Revolución Científica, que ha perdurado hasta la fecha y que se convertiría en un elemento fundamental del sistema científico, fueron las revistas, como las Philosophical Transactions de la Royal Society, cuyo primer número apareció en marzo de 1665, o las Acta Eruditorum (1682) y el Nouvel Journal des Sçavans (1698), en donde se publicaron descripciones de muchas de las principales investigaciones de la época. (Naturalmente, el que pudiesen existir revistas científicas —lo mismo que libros que, aunque fuese en ediciones limitadas, se difundían a lo largo de diferentes territorios— fue posible gracias a la invención de la imprenta, concretada en la publicación, a cargo de Johannes Gutenberg [c. 1398-1468], de la Biblia de 42 líneas en 1455.)

Y ahora, ya sí, es el momento de entrar de lleno en la biografía y ciencia del «grande entre los grandes»: Isaac Newton.

Isaac Newton

Newton, en mi opinión la mente más poderosa de la que tiene constancia la humanidad, nació en las primeras horas del día de Navidad de 1642. Hijo póstumo —y prematuro— de un pequeño agricultor, creció en la casa paterna, un caserío de Woolsthorpe, en Linconshire (Inglaterra). En 1645, su madre, Hannah, se casó de nuevo, esta vez con un clérigo: Barnabas Smith (1582-1653), rector de North Witham. Isaac no acompañó a su madre, permaneciendo con su abuela en Woolsthorpe, cerca —2 kilómetros— desde el punto de vista de las distancias, pero lejos, muy lejos, desde el más relativo, aunque no menos real, de las emociones. Barnabas, que entonces tenía sesenta y tres años, vivió hasta los setenta y uno y Hannah tuvo tres hijos con él, con los que regresó a Woolsthorpe en 1653. Todos estos hechos no debieron ser fáciles para un espíritu tan obsesivo como el de Newton, dando ocasión, siglos más tarde, a que algunos investigadores (como Frank E. Manuel) explorasen su subterráneo y poderoso universo mental recurriendo a enfoques psicoanalíticos.

La carrera universitaria, y a la postre científica también, del joven Isaac comenzó en los primeros días de junio de 1661, cuando fue admitido en el Trinity College de Cambridge. Aunque gozó del privilegio de recibir una educación superior, lo hizo con la limitación de ingresar en la Universidad como subsizar, es decir, como un estudiante pobre, que pagaba su estancia con trabajos serviles para los fellows (miembros del college) y estudiantes más ricos. El orgullo, el inmenso orgullo, de Isaac debió de sufrir ante semejante situación. En cualquier caso, de lo que no hay duda es de que las habilidades y conocimientos de Newton florecieron en Cambridge, lugar que sería su hogar durante una buena parte de su vida, hasta que en 1696, ya reconocido y poderoso, abandonó las orillas del Cam por Londres, para implicarse en la dirección del Mint, la Casa de la Moneda inglesa.

Un momento culminante de su estancia en Cambridge fue cuando, en 1669, obtuvo la cátedra lucasiana (instituida en 1663 con las rentas de las cien libras que dejó para tal fin en su testamento Henry Lucas), lo que haría posible que se dedicase por completo a la filosofía natural, completando una obra científica tan extraordinaria que no es posible hacerle justicia en pocas palabras.

Grabado de Sébastien Le Clerc en que aparece Luis XIV (con sombrero de plumas) visitando la Académie des Sciences en 1671. Junto a él, su ministro de Finanzas y responsable principal de la organización en 1666 de la academia, y en la lejanía, construyéndose, el observatorio astronómico de la Académie.

Aunque el campo de sus intereses científicos fue muy amplio, donde Newton alcanzó su mayor altura fue en matemáticas y física, dos ciencias íntimamente relacionadas entre sí, como ya tuve ocasión de comentar en el capítulo anterior; la física, recordemos una vez más, pretende codificar en forma de expresiones matemáticas las regularidades que detectamos en la naturaleza. Newton se aprovechó especialmente de este hecho, ya que una de sus grandes —sin duda la mayor— aportaciones a la matemática, la versión del cálculo diferencial denominada cálculo de fluxiones, le permitió explorar con una precisión y seguridad antes desconocida el universo de los movimientos. No es, por supuesto, que todo problema matemático tenga que poseer una conexión física, y el propio Newton planteó y resolvió muchas cuestiones matemáticas puras, tantas que habría pasado a la historia de la ciencia aunque no hubiera escrito una sola línea sobre los fenómenos que tienen lugar en la naturaleza, pero no hay duda de que su gran momento tuvo que ver con la manera en que combinó matemáticas (mezclando el antiguo, tradicional, estilo geométrico euclidiano con el fluxional) y física, una combinación con la que de hecho estableció el método científico de la ciencia moderna, y que alcanzó su cumbre con la publicación, en 1687, de uno de los clásicos universales de la ciencia: Philosophiae Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural), seguramente el tratado científico más influyente jamás escrito. Pero es pronto todavía para abordar los Principia.

Por lo que sabemos, la base del método newtoniano de las fluxiones, que introdujo una profunda revolución en la matemática, data del verano de 1665, encontrándose expuesto en un tratado de octubre de 1666, aunque su desarrollo más completo aparece en De methodis fluxionum et serierum infinitorum (1670-1671). Ninguno de estos trabajos fue publicado entonces: el de 1665, vería la luz de la letra impresa en 1967, el de 1666 en 1962, y el de 1670-1671 en 1736.

La matemática newtoniana frente a la analítica

El método fluxional fue la primera versión de cálculo diferencial ideada, pero pronto encontró un competidor: el cálculo infinitesimal desarrollado por otro gigante: Gottfried Wilhelm Leibniz. Ambos métodos son virtualmente idénticos, lo que no quiere decir que sean igualmente recomendables. Pero antes de entrar en este punto, es inevitable referirse a la agria polémica que surgió entre ambos pensadores y sus respectivos seguidores a propósito de la prioridad en la invención.

Se ha escrito tanto sobre aquella polémica, que destiló enormes dosis de maldad, vanidad y mezquindad en espíritus supuestamente elevados, que lo mejor es limitarse a apuntar algunos datos. Así, no hay dudas acerca de la prioridad de Newton, una prioridad que se complicó (en lo que a reconocimiento público se refiere) debido al patológico rechazo de éste a que se publicasen sus descubrimientos. Pero a pesar de esa aversión, algunos datos salieron de su estudio:

Isaac Barrow envió a John Collins (1625-1683) una copia de uno de los manuscritos newtonianos, De analysi per æquationes, que versaba sobre las series infinitas en su aplicación a las cuadraturas, una cuestión no centrada en el cálculo fluxional, pero sí relacionada con él. Desde entonces Collins (que preparó una copia de De analysi para su propio uso) persiguió con ahínco a Newton, cuyo genio matemático reconoció. Uno de los frutos de esa persecución fue la carta que el 10 de diciembre de 1672 le escribió Newton, en la que incluía como comentario aparentemente casual, sin entrar en detalles, que había desarrollado un método general que además de permitirle encontrar la tangente a cualquier curva (la esencia, recordemos, de la derivación), servía asimismo para resolver «otros tipos de problemas más abstrusos», como longitudes, áreas o centros de gravedad de curvas. Cuestiones estas, por supuesto, que constituyen el primer objetivo de un cálculo diferencial e integral.

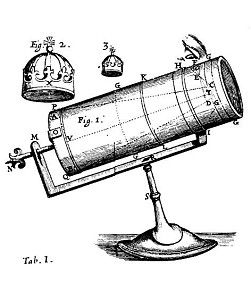
Telescopio reflector construido por Newton. Dibujo incluido en su artículo «An accompt of a new catadioptrical telescope invented by Mr. Newton» (1672).

Cuando el secretario de la Royal Society, Oldenburg, una de cuyas funciones era, como ya apunté, mantener una red de corresponsales a los que informaba de logros científicos de interés, pidió ayuda a Collins para que le contase acerca de qué trabajos matemáticos se estaban llevando a cabo en Inglaterra, éste preparó un extenso sumario (conocido como Historiola), que incluía detalles de la carta de Newton de diciembre de 1672. Y en este punto entra en la historia Leibniz, que visitó Londres entre enero y marzo de 1673: allí conoció a Oldenburg, quien poco después, el 6 de abril, le envió una carta en la que utilizaba el informe preparado por Collis. En el otoño de 1675, Leibniz desarrollaba las ideas principales de su cálculo diferencial. El 26 de junio de 1676, Oldenburg enviaba a Leibniz un resumen de la Historiola; éste, a su vez, realizó una nueva visita a Londres en octubre, momento en el que Collis le mostró su copia de De analysi y la versión completa de la Historiola. Todo, absolutamente todo, sin que Newton supiera nada. En 1684, Leibniz sacaba a la luz Nova methodus pro maximis et minimis, su primera publicación sobre el cálculo, que se limitaba a la diferenciación; en 1686 aparecía De geometria recondita, que ya incluía la integración.

Está claro, por consiguiente, que Newton fue el primero en descubrir el cálculo diferencial. Menos claro es cuál fue la deuda de Leibniz a los escritos newtonianos a que tuvo acceso, no muy explícitos, desde luego. En el peor de los casos, siempre se podría decir aquello que escribió Bernard le Bovyer de Fontenelle (1675-1757), el literato secretario perpetuo de la Académie des Sciences de París, quien en el éloge que dedicó a Newton, como associé étranger, tras la muerte de éste, escribió: «y si [Leibniz] tomó [el cálculo diferencial] de sir Isaac, al menos se asemejó al Prometeo en la fábula, que robó fuego a los Dioses para dárselo a la humanidad». Para Fontenelle, Newton era, por supuesto, uno de esos Dioses.

Pero Leibniz hizo mucho más que poner a disposición del mundo un precioso instrumento que Newton no parecía dispuesto a compartir. La versión leibniziana del cálculo ofrece muchas ventajas. La notacional es una de ellas: la que él diseñó se ha mantenido, prácticamente inalterada, hasta la fecha. Y no es la única, ni siquiera la principal ventaja: la versión newtoniana del cálculo depende mucho más de la idea (e imagen) de movimiento que la de Leibniz; es, en consecuencia, menos poderosa a la hora de manipular formalmente ecuaciones; menos, en definitiva, abstracta. El cálculo diferencial de Leibniz se amoldó perfectamente a (más bien, habría que decir que propició) la revolución analítica que se introdujo en la matemática europea durante la segunda mitad del siglo XVIII.

Pero la revolución analítica se afincó sobre todo en el continente europeo, no en las Islas Británicas, en donde su entrada tardó en producirse, debido, precisamente, al prestigio de Newton. Sería gracias a William Whewell (1794-1866) que esta situación comenzaría a cambiar. En su influyente tratado The Philosophy of the Inductive Sciences (1840), Whewell, que ocupó cátedras de mineralogía y filosofía moral en Cambridge, siendo, además, master del Trinity College entre 1841 y 1866, expresó excelentemente la situación: «Los métodos sintéticos de investigación seguidos por Newton fueron… un instrumento, sin duda poderoso en su excelsa mano, pero demasiado pesado para que lo pudieran emplear con éxito otras personas. Los compatriotas de Newton fueron los que más tiempo se adhirieron a tales métodos, debido a la admiración que sentían por su maestro y, por este motivo, los cultivadores ingleses de la astronomía física se quedaron rezagados frente a los progresos de la ciencia matemática en Francia y Alemania, por un gran margen que sólo recientemente han superado. En el continente, las ventajas ofrecidas por el uso habitual de símbolos, y por la atención prestada a su simetría y otras relaciones, fueron aceptadas sin reserva. De esta manera, el Cálculo Diferencial de Leibniz que fue, en su origen y significado, idéntico al Método de Fluxiones de Newton, pronto sobrepasó a su rival en la extensión y generalidad de sus aplicaciones a problemas». Como saben muy bien los estudiosos de la economía, ser el primero no siempre es lo mejor: introduce unas ligaduras de las que no es fácil desprenderse.

Investigador de la naturaleza

A la par que sus indagaciones matemáticas, Newton comenzó a explorar el mundo de la naturaleza. Estimulado por los cursos de óptica de Barrow en Cambridge y la teoría de la luz de Descartes, hacia 1664 empezó a interesarse por los fenómenos ópticos. No fue, sin embargo, hasta 1666 (año que pasó en la finca familiar de Woolsthorpe debido a una epidemia que obligó a cerrar la universidad en agosto de 1665) cuando intensificó sus esfuerzos, recurriendo a un instrumento simple pero en sus manos extremadamente precioso: un prisma de vidrio. He aquí como se refirió al inicio de sus experimentos en el artículo que publicó en el número del 19 de febrero de 1672 de las Philosophical Transactions de la Royal Society: «A comienzos del año 1666 (momento en el que me apliqué a pulir cristales ópticos de formas distintas a la esférica) me proporcioné un prisma triangular de cristal, para ocuparme con él del celebrado Fenómeno de los Colores. Habiendo oscurecido mi habitación, hice un pequeño agujero en una contraventana, para dejar pasar sólo una cantidad conveniente de luz del Sol, y coloqué mi prisma en su entrada, de manera que pudiese ser refractado en la pared opuesta. Al principio, ver los vivos e intensos colores así producidos constituyó una muy entretenida distracción, pero después de un rato intentando considerarlos más cuidadosamente, me sorprendió verlos en forma oblonga, cuando, según las leyes aceptadas de la Refracción, esperaba que hubiesen sido circulares».

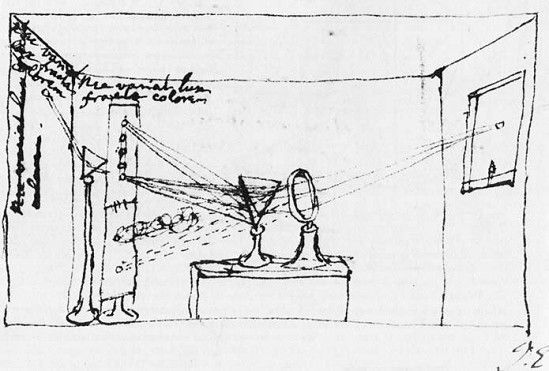
Esbozo debido al propio Isaac Newton de uno de sus experimentos sobre la luz y los colores. En la parte superior, a la izquierda, se lee: «Nec variat lux fracta colorem» («Tampoco la luz refractada cambia de color [en una segunda refracción]»). Manuscrito de 1721 (Bodleian Library, Oxford University).

Semejante anomalía le indujo a recurrir a un segundo prisma, con el que llegó a la conclusión de que los colores (observados desde hacía ya siglos) que aparecían al pasar la luz blanca por los prismas no eran «cualidades de luz, derivadas de refracciones o reflexiones de cuerpos naturales (como se cree generalmente), sino propiedades originales o innatas». La luz visible se convertía, en consecuencia, en la combinación de diferentes colores elementales, como muestra con particular claridad el arco iris.

Portada de I. Newton, A Treatise of the Method of Fluxions and Infinite Series, publicado en 1737, pero escrito por Newton (en latín) en 1671.

Página de Gottfried W. Leibniz, «Nova methodus pro maximis & minimis» (Acta Eruditorum, 1684).

Sus análisis de la dispersión y composición de la luz le sugirieron una forma de perfeccionar el telescopio, el instrumento indispensable para escudriñar el cosmos desde que Galileo lo introdujera para tales fines a comienzos de aquel siglo: comprendiendo que era, como escribió en la Óptica, «un intento desesperado el mejorar los telescopios de longitudes dadas, por refracción», construyó un telescopio reflector, que utilizaba dos espejos (uno curvo y otro plano) y que superaba a los hasta entonces en uso, eliminando la aberración cromática producida por las lentes. De hecho construyó dos: uno lo guardó para utilizarlo él mismo y el otro lo donó a la Royal Society, como reconocimiento por haberle elegido uno de sus miembros (el número 290) el 11 de enero de 1672. Llegaría el día en que sería el todopoderoso presidente de esa sociedad.

El anuncio realizado en el número del volumen correspondiente a 1672 de las Philosophical Transactions de sus observaciones e interpretaciones en el dominio de los fenómenos ópticos, dio origen a una de las cosas que Newton más detestaba: la polémica. Y si la detestaba era, por encima de todo, porque significaba que su autoridad era cuestionada, algo que él no podía aceptar. Humilde, ciertamente, nunca fue; sí, por el contrario, huraño, susceptible y desconfiado (alguien dijo de él que padecía de un tipo de lo que vulgarmente llamamos neurosis aguda en grado extremo. «Uno de los más temerosos, cautos y suspicaces temperamentos que jamás conocí», aseguraba William Whiston, su sucesor, como ya señalé, en la cátedra lucasiana). Entró en conflicto, en particular, con Robert Hooke (1635-1703), el conservador (curator) de la Royal Society, magnífico científico él mismo (entre sus obras se encuentra la célebre Micrographia [1665], una de las obras fundacionales de la microscopía). Aquel agrio choque retraería aún más a Isaac de cualquier inclinación a publicar sus resultados, como se pondría de manifiesto más tarde a propósito de los Principia, y explica en parte también por qué tardó tanto en dar a la imprenta la obra en la que englobó sus investigaciones e ideas ópticas: hasta 1704 no apareció la Óptica, su «otro» gran libro.

La Óptica es una obra mucho más accesible que los Principia. Esto es debido a que su componente matemático es muy pequeño y elemental, fruto, naturalmente, de la inexistencia entonces de una teoría general de los fenómenos de que se ocupa. Aun así, se trata de un libro en el que se observa con prístina claridad un componente básico del método newtoniano: la relación dialéctica entre observación e interpretación teórica. Más que Newton, el matemático, el protagonista principal de este texto es Newton el hábil experimentador. Digno de reseñar es, asimismo, la inclusión de una serie de «Cuestiones» (ya he utilizado alguna) en las que proponía «algunos interrogantes para que otros emprendan ulteriores investigaciones». Independientemente de su valor para tan, en principio, noble fin como el de estimular a otros, las «Cuestiones» de la Óptica constituyen una de las raras ocasiones en las que Newton, el Newton que hizo norma de comportamiento el «Hipothesis non fingo» («No hago hipótesis») —aunque, por supuesto, las hiciese—, expresaba opiniones que no podía defender con argumentos firmes. No es, desde luego, frecuente encontrarse con textos publicados mientras vivía en los que se lean sentencias como: «¿Acaso el calor de la habitación templada no se transmite a través del vacío por las vibraciones de un medio más sutil que el aire y que permanece en el vacío una vez eliminado el aire?» (Cuest. 18; 2.ª edición), o «¿Acaso el movimiento animal no se debe a las vibraciones de este medio, excitadas en el cerebro por el poder de la voluntad y propagadas desde ahí a través de los capilamentos sólidos, transparentes y uniformes de los nervios hasta los músculos, a fin de contraerlos y dilatarlos?» (Cuest. 24).

Portada de la primera edición de los Principia de Newton (Londres, 1687).

Las investigaciones ópticas ofrecen una magnífica oportunidad para acceder a facetas de la personalidad de Newton que, sin ser ignoradas, han quedado con frecuencia en un segundo plano, debido, precisamente, a sus grandes éxitos como matemático y, como diríamos hoy, físico teórico. Además de las recogidas en las «Cuestiones», otra es su gran destreza manual y extraordinario poder de introspección concentrada y sostenida. Una destreza manual que llegó a aplicar a sí mismo: en algunos de sus experimentos tomó una aguja de zurcir y, utilizando su propia descripción del hecho, «la puse entre mi ojo y el hueso tan cerca como pude de la parte posterior de mi ojo». Luego, en un ensayo cuyo solo pensamiento le pone a uno enfermo, empujó la aguja contra el globo ocular una y otra vez hasta que aparecieron —le cito de nuevo— «varios círculos blancos, oscuros y coloreados», círculos que «siguieron haciéndose evidentes cuando seguí frotando mi ojo con el extremo del punzón; pero si mantenía mi ojo y el punzón quietos, aunque continuara apretando mi ojo con él, los círculos se hacían más débiles y a menudo desaparecían hasta que seguía el experimento moviendo mi ojo o el punzón».

¿Sorprenderá que pudiese ser cruel con otros, él, que fue cruel incluso consigo mismo?

Los Principia

Pero ya es hora de referirse a su obra suprema: Philosophiae Naturalis Principia Mathematica.

Las circunstancias que rodean la génesis del contenido de este libro, así como el que Newton aceptase prepararlo y que fuese publicado, me llevarían demasiado lejos, aunque, ciertamente, hay que recordar —y agradecer— la participación decisiva de alguien cuyo nombre es recordado por otros, en última instancia menos trascendentales, menesteres: el astrónomo Edmond Halley (1656-1742), quien logró vencer la resistencia de Newton, pagando además de su propio bolsillo los gastos de la edición. Me limitaré a algunos apuntes relativos a sus contenidos.

Lo primero que hay que decir es que los Principia es una obra compleja y difícil. Entre sus múltiples aportaciones destaca, constituyendo lo que se puede denominar su núcleo central, el que en ella Newton desarrolló un sistema dinámico basado en tres leyes del movimiento; leyes que, a pesar de que hoy sabemos —desde que Albert Einstein formulara en 1905 la teoría especial de la relatividad— que no son completamente exactas, constituyen el fundamento de la inmensa mayoría de los instrumentos móviles de que disponemos (incluyendo las sondas espaciales que investigan el espacio profundo). Jamás leyes de una teoría científica han influido más en la humanidad que estas tres leyes newtonianas. Hay que señalar, no obstante, que la historia de la mecánica newtoniana no terminó en 1687: los Principia, por ejemplo, no contienen principios como los de conservación del momento o de la energía, que hoy consideramos aspectos muy importantes de la mecánica teórica.

Otra joya suprema de los Principia es la ley de la gravitación universal, que permitió contemplar como manifestaciones de un mismo fenómeno la caída de graves en la superficie terrestre y los movimientos de los planetas. Esta ley no hace su aparición en los Principia hasta el libro tercero, Sobre el sistema del mundo; más concretamente, y tras una elaborada gestación, en la «Proposición VII. Teorema VII» y sus dos corolarios («La gravedad ocurre en todos los cuerpos y es proporcional a la cantidad de materia existente en cada uno», y «La gravitación hacia cada partícula igual de un cuerpo es inversamente proporcional al cuadrado de la distancia de los lugares a las partículas»). Nunca volvería la humanidad a mirar al universo de la manera en que lo había hecho hasta entonces. La fuerza que atraía a los planetas entre sí y la responsable de la caída de los cuerpos en las proximidades de la superficie terrestre resultaban ser la misma, y una sencilla fuerza, la del inverso del cuadrado de la distancia (con la que, utilizando sus poderes matemáticos, Newton pudo deducir las trayectorias elípticas encontradas por Kepler), bastaba para explicar sus aspectos más fundamentales.

Estas eran las vigas maestras del sistema newtoniano del mundo, pero ¿qué instrumento/concepto introdujo Newton para explicar cómo se relacionan entre sí los cuerpos sometidos al imperio de las leyes que había diseñado? La respuesta que se da en los Principia es: mediante fuerzas «a distancia»; esto es, fuerzas que no necesitan ningún soporte (o medio) para ir de un cuerpo a otro. No es preciso elaborar mucho para darse cuenta de que se trata de una idea francamente contraintuitiva. Pero funcionaba, para horror de, entre otros, aquellos que defendían el sistema del mundo —basado en un plenum colmado de vórtices/remolinos— que Descartes había propugnado en diversos lugares, como en sus Principia philosophiae (1644). Y Newton fue lo suficientemente buen científico como para no renunciar a un instrumento conceptual que mostraba su valor predictivo, por muy extraño que fuese. Otra cosa es lo que él pensase, sin poderlo demostrar. Y qué pensaba acerca de esas misteriosas fuerzas a distancia es algo que sabemos a través de una carta que envió el 25 de febrero de 1693 a Richard Bentley (1662-1742), quien intervino en la preparación de la segunda edición de los Principia:

Es inconcebible que la materia bruta inanimada opere y afecte (sin la mediación de otra cosa que no sea material) sobre otra materia sin contacto mutuo, como debe ser si la gravitación en el sentido de Epicuro es esencial e inherente a ella. Y esta es la razón por la que deseo que no me adscriba la gravedad innata. Que la gravedad sea innata, inherente y esencial a la materia de forma que un cuerpo pueda actuar a distancia a través de un vacío sin la mediación de otra cosa con la cual su acción o fuerza puede ser transmitida de [un lugar] a otro, es para mí algo tan absurdo que no creo que pueda caer en ella ninguna persona con facultades competentes de pensamiento en asuntos filosóficos.

Isaac Newton en 1726, cuando se publicó la tercera edición de los Principia, que aparece abierto sobre la mesa.

Existe otro aspecto de los Principia que conviene destacar: el que constituye el ejemplo supremo de lo que puede denominarse el «método newtoniano». Y es que Newton nos legó en ese libro —en otras obras también, pero sobre todo en esta— lo que constituye la esencia del método científico moderno: la elaboración de modelos matemáticos simples que se comparan con los fenómenos naturales, comparaciones de las que surgen nuevas versiones, más complicadas, de los modelos previos. Con él, en definitiva, la matemática se encarnó verdaderamente en la esencia de la teoría física.

Un personaje poderoso

El, a la postre, inmenso poder explicativo y predictivo de sus contribuciones científicas, condujo a que Newton se convirtiese en un personaje poderoso. Ya en enero de 1689 fue elegido miembro del Parlamento en representación de su Universidad. Pero la gran oportunidad tardaría todavía siete años en llegar: en abril de 1696, como ya indiqué, tomaba posesión del puesto de warden (guardián) del Mint, la Casa de la Moneda inglesa, lo que implicaba trasladarse a vivir en Londres y, por supuesto, magníficas retribuciones. En febrero de 1700, ascendía en esta escala oficial, pasando a ocupar el puesto de master (maestro, el equivalente a director o presidente) del Mint. Finalmente, el 10 de diciembre de 1701 renunciaba a su cátedra de Cambridge. Su vida, sus aspiraciones, eran ya otras. Pero no renunciaba a acumular más poder: el 30 de noviembre de 1703 fue elegido presidente de la Royal Society. Y a fe que ejerció el poder que el puesto le confería: que le preguntasen si no a John Flamsteed (1646-1719), el astrónomo real, al que presionó con toda la dureza —y triquiñuelas— de que era capaz para obtener las tablas astronómicas que éste había preparado durante años, y que eran su principal tesoro, pero que Newton necesitaba para componer una teoría de las mareas, que añadir a una nueva edición de los Principia.

Pero ningún humano, por aparentemente sobrehumano —e inhumano— que parezca, escapa de ese final que es la muerte. Isaac Newton, el gran Isaac, murió el 20 de marzo de 1727. Era por entonces un hombre muy rico, y continuó recibiendo honores: el 4 de abril fue enterrado en la abadía de Westminster, donde todavía hoy se puede contemplar su tumba. Dos versos de Alexander Pope (1688-1744), inicialmente compuestos para ser inscritos en el monumento que se iba a erigir en su honor en la abadía, dan idea de los sentimientos de admiración y respeto que el autor de los Principia suscitaba ya entonces:

Seguramente él habría aceptado con gusto semejante caracterización, aunque en alguna ocasión dio muestras de alguna modestia, una circunstancia rara en él. «Si vi más lejos, fue porque permanecí a hombros de gigantes», escribió en 1676 a Robert Hooke. A mí, sin embargo, me gusta más otra de sus frases, igualmente famosa: «No sé lo que podré parecer al mundo, pero yo me veo a mí mismo únicamente como si hubiese sido un niño que juega en la orilla del mar, y que se divirtió encontrando de vez en cuando un guijarro más liso y una concha más bella que las normales, mientras que el gran océano de la verdad permanecía sin descubrir ante él».

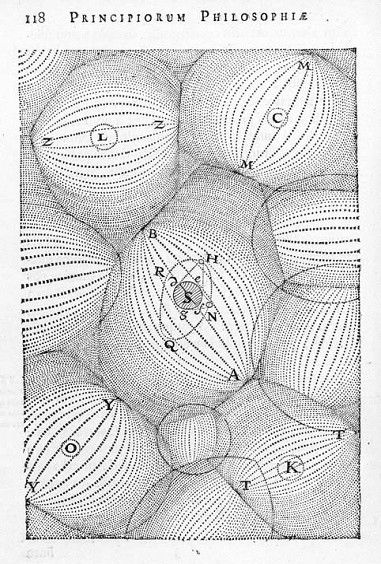
El mundo como un continuo. Lámina representando los vórtices cartesianos, incluida en René Descartes, Principia philosophiae (Amsterdam, 1644).

Epílogo

Honramos a Isaac Newton como un gran científico, para algunos el más grande de la historia. No le recordamos como un profeta. Sin embargo, en otro tiempo, bajo otras circunstancias, acaso la historia le habría terminado considerando como tal. No pudo presumir, como su tan admirado Ezequiel (40:4), que un ángel le había visitado para decirle: «Hijo de hombre, mira bien, escucha atentamente y presta atención a todo lo que te voy a mostrar, porque has sido traído aquí para que yo te lo muestre». Pero en su ambición suprema, quiso alcanzar, mediante el incomparable instrumento de su inteligencia (probablemente lo más próximo a divino que se pueda encontrar en esta terrenal única tierra nuestra), el conocimiento que —según las Sagradas Escrituras— los ángeles habían ofrecido, gratuitamente, a los profetas. En la soledad de sus habitaciones, luchando con manuscritos oscuros y complejos, aquel Isaac —para mí mucho más grande que el bíblico— debió con frecuencia tronar, indignado, contra semejante injusticia. ¿Por qué se le negaba a él lo que otros tan fácilmente habían logrado? Su vida, sus millones de palabras escritas —y las muchísimas más que leyó—; las horas, los días, meses y años inacabables en los que pugnó por comprender los mensajes divinos, no son sino testimonio de cuánto se rebeló y cuánto deseó.

Portada de la primera edición de la Opticks (Londres, 1704) de Newton.