Aunque no todos los sistemas científicos se expresan en términos matemáticos (pensemos, sin ir más lejos, en El origen de las especies de Darwin —¿negará alguien que se trata de una obra científica?—, en cuyos centenares de páginas no aparece ninguna expresión matemática), es indudable que la matemática desempeña un papel muy importante en la ciencia. Los procedimientos y resultados matemáticos poseen una seguridad, claridad e inevitabilidad (una vez fijados los axiomas de partida, por supuesto) tal como no se encuentra en ninguna otra disciplina científica. Precisamente por esa firmeza e inevitabilidad hay quien argumenta que la matemática no es realmente una ciencia, no al menos como lo pueden ser la biología, la química, la fisiología, la geología o la física. Mientras que éstas serían sistemas de proposiciones a posteriori, falibles, la matemática sería a priori, tautológica e infalible. A pesar de que se pueden encontrar manifestaciones suyas que apuntan en direcciones bastante diferentes, la frase que John Stuart Mill (1806-1873) escribió en uno de sus libros, A System of Logic, Ratiocinative and Inductive (Un sistema de lógica racionalizadora e inductiva; 1843), «la lógica no observa, ni inventa, ni descubre; pero juzga», expresa de manera espléndida semejante idea, que de alguna forma refleja el lugar tan peculiar que ocupa la matemática con respecto a las ciencias de la naturaleza.

Sea o no una ciencia, de lo que no hay duda es de que, como apuntaba antes, la matemática desempeña un lugar central en las ciencias de la naturaleza, especialmente en la física. «Sostengo», afirmó Immanuel Kant (1724-1804) en el «Prefacio» de su Metaphysische Anfangsgründe der Naturwissenschaft (Fundamentos metafísicos de la ciencia natural; 1786), «que solamente se encuentra genuina ciencia en una teoría natural especial en la medida en que se encuentre matemática en ella». Una afirmación que aunque exagerada (recordemos el ejemplo de Darwin), posee más de un grano de verdad. En efecto, para cumplir con su objetivo de describir los fenómenos que tienen lugar en la naturaleza —tarea que incluye predecir las condiciones en que se volverán a producir—, la ciencia, y a su cabeza, en este sentido, la física, intenta recurrir a leyes que se expresan matemáticamente, hasta el punto de que se podría decir que no hay física, tal y como la entendemos en la actualidad, sin matemática.

Pero dejemos todo esto, al menos por el momento, y pasemos a tratar algunos aspectos de la historia de la matemática, dando, como veremos, un papel especial a Euclides y Gödel.

Aunque es difícil establecer algo así como un momento o período del que se pueda decir, «entonces comenzó el largo camino de la ciencia», sí que se puede afirmar que cuando se encuentran los primeros logros con alguna significación científica, éstos estaban relacionados con la matemática. Así ocurre, por ejemplo, con el hallazgo de huesos de animales de bastantes miles de años de antigüedad, provistos de series de muescas, que constituyen auténticas «máquinas de contar» primitivas, y con las que nuestros antepasados estaban sentando las bases de la matemática. Uno de los más conocidos de estos huesos fue el descubierto en la década de 1950 en Ishango, en lo que ahora es Zaire, por Jean de Heinzelin, cuya antigüedad se sitúa entre el 9000 y el 6500 a.C. Con el paso del tiempo, aquellos procedimientos tan simples darían paso a otros mucho más elaborados. Así, y pasando por alto otros sistemas anteriores, cuya influencia posterior ha sido escasa, hay que citar las contribuciones de los sumerios, un pueblo que se instaló en el valle del Tigris y el Éufrates. Hacia el cuarto milenio a.C. los sumerios desarrollaron un sistema de numeración basado en la agrupación en sesentenas o potencias de 60. Este sistema sería transmitido, por mediación de los babilonios y luego de los griegos y los árabes, en la expresión del tiempo en horas, minutos y segundos, y en la de los arcos y ángulos en grados, minutos y segundos. El porqué los sumerios introdujeron una base tan elevada es todavía hoy un misterio, aunque se han manejado varias hipótesis, como la de que eligieron el 60 por su propiedad de ser divisible por los seis primeros números enteros.

En cuanto al sistema decimal, el que finalmente más se extendió, acompañándonos, casi universalmente, hasta la actualidad, se han encontrado rastros de su utilización en épocas y escenarios no muy alejados del de los sumerios: cuando, con la ayuda de la Piedra Rosetta, descubierta en 1799 durante la expedición napoleónica a Egipto, se pudo descifrar la escritura jeroglífica egipcia, se encontró que su sistema de numeración, que data de hace unos 5.000 años, estaba estructurado según la base 10, aunque empleando símbolos que hacían muy engorrosa su utilización.

Contar ha sido siempre una necesidad de los humanos, pero existe al menos otra estrechamente relacionada con lo que más tarde sería el conocimiento científico, una necesidad que surgió según se iban haciendo más complejos los sistemas de organización social. Me estoy refiriendo a la astronomía y al establecimiento de calendarios, dominios relacionados muy estrechamente con la matemática.

La astronomía desempeñó un papel central en el mundo babilónico, el mundo de la dinastía semítica de Hammurabi de Babilonia (de la palabra griega para la ciudad de Babel, al sur del actual Bagdad), que hacia el 1700 a.C. tomó el relevo de los sumerios. Los babilonios colocaron la Tierra en el centro del universo, parece que inventaron el zodiaco y se preocuparon especialmente por conservar registros de los movimientos de la Luna. Introdujeron un año que constaba de 360 días, dividido en 12 meses de 30 días cada uno; además crearon la semana, bautizando los días por el Sol, la Luna y los cinco planetas entonces conocidos. También fueron los responsables de la división del día en dos períodos de doce horas y descubrieron los movimientos aparentemente anómalos (retrogresiones) de algunos planetas —como Marte— y del Sol. Es obvio, por consiguiente, que nuestra cultura es profundamente deudora de los conocimientos e iniciativas surgidos en aquel imperio. Impulsados por estos intereses, avanzaron también en la geometría: sabían, por ejemplo, que los triángulos inscritos en un semicírculo eran rectángulos, y parece que conocían el denominado teorema de Pitágoras (la suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa), aunque como en toda su ciencia lo expresaban a través de casos particulares.

Utilizando como excusa el ejemplo que acabo de citar del teorema de Pitágoras, es importante señalar que otras civilizaciones también mostraron algún tipo de conocimiento de él; lo que quiere decir —es el punto que quiero destacar— que los orígenes de los saberes matemáticos se encuentran mucho más extendidos de lo que muchos piensan, un hecho que puede también tomarse en el sentido de que el tipo de razonamiento que caracteriza a la matemática se halla firmemente enraizado en nuestro sistema cognitivo; esto es, en la mente de los humanos. Así, estudiando altares construidos en India y descritos en el conjunto de escritos conocidos como Sulvasutras (expresión que significa «reglas de cuerdas»), que probablemente se remontan a una época no muy alejada de la del propio Pitágoras, se ha encontrado que el conocimiento expresado por el teorema de Pitágoras se utilizó para construir un cuadrado de área igual a la de un rectángulo dado. Asimismo, A. Thom y A. S. Thom descubrieron que en la construcción de monumentos megalíticos situados en el sur de Inglaterra y Escocia se utilizaron «triángulos pitagóricos», esto es, triángulos rectángulos cuyos lados son múltiplos enteros de una unidad fundamental de medida. En un sentido parecido, al comparar manuscritos chinos antiguos con colecciones de problemas matemáticos babilónicos, B. L. Van der Waerden, uno de los historiadores más eminentes de la matemática antigua, encontró tantas analogías que no pudo evitar concluir la posible existencia de una fuente común prebabilónica; en otras palabras: que debió existir ya una matemática en el Neolítico, esto es, entre, aproximadamente, el 3000 y 2500 a.C., que se había extendido desde Europa central hasta las Islas Británicas, el Oriente Próximo, India y China.

En vista de lo anterior, cabe preguntarse por qué nos obstinamos en dar preferencia a los griegos en nuestras exposiciones relativas a la matemática, en particular, y a la ciencia, en general. La respuesta a semejante cuestión no es difícil: en torno a los siglos V-IV a.C., en Grecia, las islas del mar Egeo y Asia Menor se produjo un cambio cualitativo en el análisis de los fenómenos de la naturaleza. «La filosofía —escribió Bertrand Russell (1872-1970) en uno de sus libros de carácter general más apasionantes, Wisdom of the West (La sabiduría de Occidente)— comienza cuando alguien plantea una cuestión general, y lo mismo sucede con la ciencia. Los primeros que experimentaron esta clase de curiosidad fueron los griegos. La filosofía y la ciencia, tal y como la conocemos ahora, son invenciones griegas.»

En efecto, con anterioridad a los griegos el «conocimiento científico» —y a su cabeza el matemático, el primero en el que se encontraron «verdades» que todavía hoy sostenemos— se expresaba básicamente a través de casos particulares. En esta característica reside la distancia que separaba a babilonios o hindúes y sus contemporáneos y predecesores de lo que es realmente la ciencia: en la capacidad de elevarse sobre situaciones particulares, construyendo leyes, insertas en un sistema lógico-deductivo, que se aplican a —o que se ejemplifican en— un conjunto, cuanto más grande mejor, de situaciones concretas. Aunque los egipcios, que realizaron aportaciones muy notables a la geometría (como calcular el área de un triángulo isósceles o el área de un campo circular), avanzaron en la senda de la abstracción, ninguna otra civilización puede competir en este punto con la helena. Sin exageración, se puede decir que fueron los griegos los que crearon realmente la ciencia, entendida ésta como un cuerpo de conocimientos organizados de manera sistemática, general y racional. Y no sólo inventaron la matemática moderna y la filosofía, y avanzaron sustancialmente en otros dominios científicos (como la astronomía, física y ciencias naturales), también escribieron por primera vez historia, en oposición a los meros anales, y especularon acerca de la naturaleza del mundo y el sentido y fines de la vida, sin verse encadenados por ninguna ortodoxia heredada.

Fue en el dominio de la matemática donde más limpiamente se pueden reconocer algunas de las novedades más importantes introducidas por los griegos en el pensamiento científico. Con anterioridad a ellos, el concepto de ciencia deductiva era desconocido; en los documentos que se han conservado de antes del período heleno no aparecen «teoremas» o «demostraciones», ni conceptos tan fundamentales como los de «deducción», «definición», «postulado» o «axioma», de cuya creación sólo ellos fueron responsables.

No resisto la tentación, en este punto, de citar un pasaje de un hermoso libro, A Mathematician’s Apology (Apología de un matemático), escrito en 1940 por el matemático británico Godfrey Harold Hardy (1877-1947):

Como la historia prueba abundantemente, los logros en matemáticas, independientemente de su valor intrínseco, son los más perdurables. Podemos ver esto incluso en civilizaciones protohistóricas. Las civilizaciones babilónica y asiria han perecido; Hammurabi, Sargón y Nabucodonosor son hoy nombres vacíos, pero las matemáticas babilónicas son todavía interesantes y el sistema sexagesimal de numeración se utiliza todavía en astronomía. Aunque, por supuesto, el ejemplo crucial nos lo proporcionan los griegos. Los griegos son los primeros matemáticos, todavía hoy «vigentes» entre nosotros. Las matemáticas orientales pueden ser una curiosidad interesante, pero las matemáticas griegas son la auténtica realidad. Los griegos utilizaron por primera vez un lenguaje matemático que todavía los matemáticos de hoy pueden entender… Arquímedes será recordado cuando Esquilo haya sido olvidado, porque las lenguas mueren y las ideas matemáticas no.

La precisión y seguridad que proporciona la matemática se alió de forma incomparable con el carácter inquisitivo de la filosofía para estudiar la naturaleza. La primera escuela de «filósofos científicos» surgió en Mileto. En aquel puerto marítimo, Tales (c. 640-546 a.C.) se formuló una de las preguntas filosóficas y científicas más básicas: «¿De qué están hechas las cosas?». Y contestó: «De agua», una respuesta no tan absurda si recordamos que el cuerpo humano está formado por cerca del ochenta por ciento de agua. Como matemático, Tales importó de sus viajes a Egipto reglas empíricas para medir terrenos, que le sirvieron para poner los cimientos de la geometría como ciencia deductiva: calculó la distancia entre los navíos desde el vértice de una torre y determinó la altura de una pirámide por la sombra que proyectaba, cualquiera que fuese la posición del Sol. Heródoto escribió que Tales predijo un eclipse de Sol, eclipse que se ha datado como el que tuvo lugar el 585 a.C. A esa época debe pertenecer, pues, aquel filósofo-científico y matemático.

Seguramente contemporáneo de Tales, a quien probablemente visitó, aprendiendo de él, es otro de los nombres inmortales que ha dejado la matemática griega: Pitágoras (c. 580-500 a.C.), natural de Samos, una de las islas del Dodecaneso, próxima a Mileto, que abandonó porque no podía soportar el gobierno del tirano Polícrates. Matemático al igual que filósofo, místico lo mismo que racionalista, fundador, tras haber viajado por lugares como Egipto y Mesopotamia, en Crotona (Italia) de una escuela —denominada «pitagórica»— que llegó a convertirse en una especie de grupo religioso, a Pitágoras, o, no se sabe realmente (no se conoce ninguna obra escrita por los pitagóricos), a miembros de su escuela, se deben, junto a su célebre, y ya mencionado, teorema, descubrimientos como el de las relaciones numéricas simples asociadas a los tonos musicales. La cuerda de un instrumento dará la octava si su longitud se reduce a la mitad, mientras que si se reduce a los tres cuartos se obtiene una cuarta, o una quinta cuando es a dos tercios; se tiene, en definitiva, que cuando dos cuerdas de un instrumento musical vibran con sonidos armónicos, sus longitudes se relacionan mediante expresiones numéricas del tipo 1/2, 1/3, 2/3…

Mención aparte merece el hallazgo de los números irracionales, al que llegaron al constatar, como una mera aplicación del teorema de Pitágoras, la inconmensurabilidad de la diagonal y el lado de un cuadrado. Ahora bien, semejante resultado violentaba un aspecto básico de su filosofía científico-religiosa, el carácter fundamental de los números enteros, motivo por el cual parece que lo guardaron en secreto celosamente. Para los pitagóricos, en efecto, todo era una encarnación de los números que se podían determinar con precisión absoluta; éstos eran la esencia del universo, y desarrollaron toda una hermenéutica de ellos.

Tales de Mileto con un discípulo en un manuscrito del siglo XII (Biblioteca Comunal de Rímini).

La fascinación por los números, al igual que la idea de que existe una profunda relación entre ellos y la naturaleza, idea que tanto debe a Pitágoras y a sus discípulos, se enraizaría firmemente en la ciencia posterior, al igual que en numerosas culturas. Ciertamente, en la griega. Un ejemplo en este sentido es el del Partenón de Atenas, en cuyo diseño participaron el escultor y arquitecto Fidias y los arquitectos Calícates e Iatino. El alzado de este famoso templo muestra varias relaciones áureas (por ejemplo, la relación entre la anchura de la fachada y la altura del templo, o entre la altura total y la de las columnas), entendiendo por «razón áurea», o «número de oro», al número 1,618033…, que posee propiedades tan sorprendentes como que tanto su cuadrado como su inverso tienen las mismas cifras decimales que él mismo, o la de ser el límite de una serie formada por el cociente de dos términos sucesivos de la denominada sucesión de Fibonacci (su verdadero nombre era Leonardo de Pisa y vivió entre 1170 y 1250), cuyo enésimo término se obtiene sumando los dos anteriores; esto es: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Esa «numerización» de la naturaleza constituye de hecho uno de los rasgos característicos del conocimiento científico, bien es cierto que sin llegar necesariamente a los extremos pitagóricos, por mucho que se puedan encontrar ejemplos, como el de Kepler, que llegó a concebir —en libros como Mysterium cosmographicum (1596) o Harmonices mundi (1619)—, en una visión no muy alejada de la que sostuvo también Platón, una «armonía universal» rigiendo el universo, que según él estaría formado por una serie de esferas, sobre las que se moverían los diferentes planetas, esferas circunscritas por los cinco poliedros regulares (tetraedro, cubo, octaedro, dodecaedro e icosaedro).

El poder, conceptual desde luego, pero también práctico, que conferían los conocimientos matemáticos no pudo por menos que impresionar a los griegos, como todavía nos impresiona a nosotros, más de dos milenios después. Así, en uno de sus Diálogos, correspondiente al libro VII de las Leyes, Platón (c. 427-347 a.C.) ponía en boca de uno de los dos protagonistas, el Ateniense, las siguientes frases: «hay aún tres materias de estudio para los hombres libres: el cálculo y los números constituyen una disciplina; también el arte de la medida de la extensión y la profundidad forman, como un único ámbito, la segunda materia, mientras que la tercera es el estudio de las revoluciones de los cuerpos celestes, cómo es el movimiento natural de unos en relación con los otros. No es necesario que la mayoría estudie todo eso hasta alcanzar un conocimiento exacto, sino unos pocos». No sería necesario, pero sí que era, añadía, «vergonzoso que el común de los ciudadanos no sepa todo lo que de ellas se dice —y hasta cierto punto con total corrección— que es indispensable para la mayoría».

Y más adelante, ante otra pregunta de Clinias, el Ateniense manifestaba: «Creo que nunca nadie podría llegar a ser en opinión de los hombres ni un dios, ni un espíritu, ni un héroe capaz de cuidar a los seres humanos con seriedad, si no practicara o conociera en absoluto [esas materias]. Estaría muy lejos de ser un hombre divino si no fuera capaz de reconocer ni el uno, ni el dos, ni el tres ni, en general, los pares y los impares, ni supiera contar, ni fuera capaz de calcular la noche ni el día y desconociera las revoluciones de la Luna, el Sol y los demás cuerpos celestes». Estremece pensar que tres mil años después no hayamos sido capaces de cumplir con tan cabal recomendación, obstinándonos en mirar a la matemática como una disciplina que sólo produce dolores de cabeza en nuestros jóvenes escolares.

El entusiasmo que despertó entre los griegos el poder conceptual y práctico de la matemática se plasmó de muy diversas maneras. Ya me he referido, a propósito de Pitágoras, a algunas de ellas, pero ahora quiero mencionar otra, que ejercería una poderosa influencia en el desarrollo de la ciencia y la filosofía durante casi dos milenios: la fascinación por el círculo. Utilizaré, de nuevo, a Platón para explicar a qué me refiero, pero antes no está de más decir unas palabras sobre la biografía de esta gran figura de la Antigüedad.

Nacido en el seno de una familia patricia de Atenas, el destino aparente de Platón era el de político, pero bajo la influencia de Sócrates (c. 470-399 a.C.), de quien fue discípulo, llegó a considerar a los políticos con mucho escepticismo, convirtiéndose en filósofo y maestro. Después de viajar durante algún tiempo, ciertamente por Sicilia, tal vez por Egipto, regresó —en el 388 a.C.— a Atenas, en donde estableció su famosa Academia, situada en una gran instalación atlética que había sido utilizada antes por maestros como él.

En las obras suyas que han sobrevivido, como el Timeo, la República o las Leyes, que adoptan la forma de diálogos, apareciendo en todas ellas la figura, idealizada, de Sócrates, Platón nos transmitió aspectos básicos del pensamiento científico heleno: como, por ejemplo, la importancia que tuvo para muchos de los científicos/filósofos de su época la geometría del círculo. Esa importancia se plasmó especialmente en la descripción de los movimientos de los cuerpos celestes, en la que los círculos, las circunferencias, reinaron supremas (pronto, es cierto, en una enmarañada mezcla de epiciclos, deferentes y excéntricas) hasta la llegada de la elipse con Kepler, ya en el siglo XVII.

En los siguientes pasajes de una de sus obras más célebres, el Timeo, encontramos algunos de los argumentos que utilizaba en la defensa del círculo, junto a otros que se refieren a la propia naturaleza del universo (como la teoría de los cuatro elementos):

[El] constructor [del mundo] lo ha compuesto… de todo el fuego, de todo el aire, de toda el agua y de toda la tierra, y no ha dejado fuera del mundo ninguna parte de ningún elemento, como tampoco ninguna cualidad. Y lo ha combinado así, primero para que fuera único, sin que fuera de él quedara nada de lo que pudiera nacer otro viviente de la misma clase; y, finalmente, para que se viera libre de vejez y enfermedades. Pues él sabía bien que, en un cuerpo compuesto, las sustancias calientes y frías y, de una manera general, todas aquellas que poseen propiedades energetizantes, cuando rodean a este compuesto desde fuera y se aplican a él sin un propósito determinado, lo disuelven, hacen entrar en él las enfermedades y la vejez y de esta manera lo hacen perecer…

En cuanto a su figura, le ha dado la que mejor le conviene y la que tiene afinidad con él. En efecto, al Viviente que debe envolver en sí mismo a todos los vivientes, la figura que le conviene es la figura que contiene en sí a todas las figuras posibles. Esta es la razón por la que Dios ha constituido el mundo en forma esférica y circular, siendo las distancias por todas partes iguales, desde el centro hasta los extremos. Esa es la más perfecta de todas las figuras y la más completamente semejante a sí misma. Pues Dios pensó que lo semejante es mil veces más bello que lo desemejante.

En cuanto a la totalidad de su superficie exterior, la ha pulido y redondeado exactamente, y esto es por varias razones. En primer lugar, en efecto, el Mundo no tenía ninguna necesidad de ojos, ya que no quedaba nada visible fuera de él, ni de orejas, ya que tampoco quedaba nada audible. No le rodeaba ninguna atmósfera que hubiera exigido una respiración. Tampoco tenía necesidad de ningún órgano, bien fuera para absorber el alimento, bien para expeler lo que anteriormente hubiera asimilado. Pues nada podía salir de él por ninguna parte, y nada tampoco podía entrar en él, ya que fuera de él no había nada. En efecto, es el Mundo mismo el que se da su propio alimento por su propia destrucción. Todas sus pasiones y todas sus operaciones se producen en él, por sí mismo, de acuerdo con la intención de su autor. Pues el que lo construyó pensó que sería mejor si se bastaba a sí mismo, en lugar de tener necesidad de alguna otra cosa. No tenían para él ninguna utilidad las manos, hechas para coger o apartar algo, y el artista pensó que no había necesidad de dotarle de estos miembros superfluos, ni le eran tampoco útiles los pies, ni, en general, ningún órgano adaptado a la marcha.

Unido a las ideas y desarrollos técnicos astronómicos de pensadores como Aristóteles (c. 384-322 a. C.) y Claudio Ptolomeo (c. 90 - c. 170), junto a las tesis defendidas por la Iglesia católica, la esencia del planteamiento que hacía Platón en el Timeo formaría la denominada visión aristotélico-ptolemaica del universo, que dominó la ciencia del cosmos —y en particular el sistema solar— hasta la llegada de Galileo Galilei, e incluso más allá, si tenemos en cuenta que detrás de las ideas propagadas y popularizadas por Platón se encontraba también la de que la estructura y los movimientos de los cuerpos presentes en la naturaleza obedecían a algo así como una «lógica matemática», entendida ésta no sólo en el sentido, de que, como afirmó Galileo en uno de sus libros, Il saggiatore (El ensayador; 1623), la ciencia «está escrita en el gran libro del universo que se encuentra siempre abierto ante nuestros ojos, [pero ese libro] es incomprensible si uno no aprende antes a comprender su lenguaje y a leer las letras en las que está compuesto. Está escrito en el lenguaje de la matemática y sus caracteres son triángulos, círculos y otras figuras geométricas sin las cuales es humanamente imposible comprender una sola de sus palabras»; entendido, digo, no sólo en este sentido, sino también en el de que esa misma estructura y movimientos debían corresponder a figuras matemáticas «bellas» (un concepto este, por supuesto, completamente subjetivo).

La nómina de filósofos-científicos griegos que con sus contribuciones influyeron, condicionándolo, en el desarrollo posterior del conocimiento es larga, muy larga, pero ninguna lista estaría completa si no incluyese un nombre: el de Euclides de Alejandría (c. 300 a.C.). George Sarton, uno de los padres fundadores de la historia de la ciencia moderna, escribió de él lo siguiente (Hellenistic Science and Culture in the Last Three Centuries B. C. [Ciencia y cultura helénicas en los últimos tres siglos a.C.]; 1959): «Todos conocemos su nombre y su obra principal, los Elementos de geometría, pero sabemos muy poco sobre él. Lo poco que sabemos —y es muy poco— lo deducimos y fue publicado después de su muerte. Esta clase de ignorancia, sin embargo, no es excepcional sino frecuente. La humanidad recuerda a los déspotas y a los tiranos, a los políticos de éxito, a los hombres con fortuna (o a algunos al menos), pero olvida a sus grandes benefactores. ¿Qué sabemos sobre Homero, Tales, Pitágoras, Demócrito…? Más aún, ¿qué sabemos sobre los arquitectos de las catedrales antiguas o sobre Shakespeare? Los grandes hombres del pasado son desconocidos, incluso aunque hayamos recibido sus obras y disfrutado de sus abundantes bendiciones».

No sabemos de él con seguridad, en efecto, ni las fechas de su nacimiento ni de su muerte; se le denomina «de Alejandría» —la ciudad fundada por Alejandro Magno en la desembocadura del Nilo en el año 331 a.C.— porque es la única ciudad con la que se le puede asociar con seguridad. Probablemente fue educado en Atenas, en la Academia de Platón, uno de los principales centros matemáticos del siglo IV a.C., y seguramente el único en el que pudo haber reunido los conocimientos que aglutinó en los Elementos. Cuando la situación política convirtió Atenas en un lugar complicado para vivir y trabajar, se habría marchado a Alejandría. La Alejandría de los Ptolomeos, en donde la filosofía fue un tanto marginada, mientras que florecieron las ciencias y la literatura, en las que los sucesores de Alejandro estaban más interesados. Los Elementos —que algunos datan en torno al 325 a.C.— fueron dedicados a Ptolomeo I Sóter, quien se supone fundó la célebre Biblioteca de Alejandría, cuyo segundo bibliotecario, por cierto, fue Eratóstenes (c. 276-196 a.C.), quizá el más grande de los antiguos geógrafos; «un matemático entre los geógrafos», entre cuyas aportaciones científicas se encuentra una técnica para medir la circunferencia de la Tierra.

Teorema de Pitágoras en una traducción de los Elementos de Euclides al árabe impresa por la Typographia Medica de Roma en 1594.

Aparentemente, mientras trabajaba en Alejandría, Euclides decidió compilar y sistematizar todos los conocimientos matemáticos realizados hasta entonces, seguramente incluidos muchos en libros que no nos han llegado (sólo ha sobrevivido un tratado matemático completo —Sobre la esfera en movimiento— anterior a los Elementos, debido a un contemporáneo de Euclides, aunque más mayor, Autólico de Pitania). Fruto de aquella decisión fueron los Elementos. No hay, en mi opinión, momento superior en la historia del pensamiento griego que el de la composición de esta obra, la obra matemática por excelencia, en la que con la precisión, elegancia y saber del cirujano mejor dotado, se compone un acabado edificio de proposiciones matemáticas a partir de un grupo previamente establecido de definiciones y axiomas, que se combinan siguiendo las reglas de la lógica.

Se trata de una obra formada por trece libros, o capítulos. Los seis primeros dedicados a la geometría plana elemental, los tres siguientes a la teoría de los números (incluyendo una demostración de la infinitud de los números primos), el décimo a los inconmesurables y los tres últimos a la geometría de los cuerpos sólidos (Euclides concluyó que los únicos poliedros posibles eran los ya citados tetraedro, cubo, octaedro, dodecaedro e icosaedro, dotados, respectivamente, de 4, 6, 8, 12 y 20 caras iguales).

Euclides da la bienvenida a estudiantes en la puerta del Círculo en el que Tartaglia está rodeado por Aritmética, Geometría, Música, Astronomía y otras disciplinas matemáticas. Un cañón que se ha disparado muestra las trayectorias definidas por Tartaglia. En el círculo más alejado se sienta Filosofía. En la banda, en la mano de Platón se lee: «Nadie que no sea experto en Geometría puede entrar aquí», mientras Aristóteles se adelanta para recibir a los estudiantes. Lámina de Nova scientia (Venecia, 1537) de Niccolò Tartaglia.

Merece la pena leer las primeras líneas de este libro grandioso, en las que se encuentra su núcleo básico, sus auténticos pilares fundacionales, aquello que parece tan evidente que tendemos a pensar que son las verdades, los elementos irreductibles de la naturaleza, y, en consecuencia, acaso de nuestro esquema mental también. A partir de ellos, ya sólo resta combinarlos y comenzar a elaborar y a enumerar proposición tras proposición.

Retrato del matemático Fray Luca Pacioli y joven desconocido, de Jacopo de Barbari (primer cuarto del siglo XVI), Museo de Capodimonte (Nápoles).

Euclides, Elementos:

DEFINICIONES

1. Un punto es lo que no tiene partes.

2. Una línea es una longitud de anchura.

3. Los extremos de una línea son puntos.

4. Una línea recta es aquella que yace por igual respecto de los puntos que están en ella.

5. Una superficie es lo que sólo tiene longitud y anchura.

6. Los extremos de una superficie son líneas.

7. Una superficie plana es aquella que yace por igual respecto de las líneas que están en ella.

8. Un ángulo plano es la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta.

9. Cuando las líneas que comprenden el ángulo son rectas el ángulo se llama rectilíneo.

10. Cuando una recta levantada sobre otra recta forma ángulos adyacentes iguales entre sí, cada uno de los ángulos iguales es recto y la recta levantada se llama perpendicular a aquella sobre la que está.

11. Ángulo obtuso es el (ángulo) mayor que un recto.

12. Ángulo agudo es el (ángulo) menor que un recto.

13. Un límite es aquello que es extremo de algo.

14. Una figura es lo contenido por uno o varios límites.

15. Un círculo es una figura plana comprendida por una línea [que se llama circunferencia] tal que todas las rectas que caen sobre ella desde un punto de los que están dentro de la figura son iguales entre sí.

16. Y el punto se llama centro del círculo.

17. Un diámetro del círculo es una recta cualquiera trazada a través del centro y limitada en ambos sentidos por la circunferencia del círculo, recta que también divide el círculo en dos partes iguales.

18. Un semicírculo es la figura comprendida entre el diámetro y la circunferencia por él cortada. Y el centro del semicírculo es el mismo que el del círculo.

19. Figuras rectilíneas son las comprendidas por rectas, triláteras las comprendidas por tres, cuadriláteras las comprendidas por cuatro, multiláteras las comprendidas por más de cuatro rectas.

20. De entre las figuras triláteras, triángulo equilátero es la que tiene los tres lados iguales, isósceles la que tiene sólo dos lados iguales, y escaleno la que tiene los tres lados desiguales.

21. Además, de entre las figuras triláteras, triángulo rectángulo es la que tiene un ángulo recto, obtusángulo la que tiene un ángulo obtuso, acutángulo la que tiene los tres ángulos agudos.

22. De entre las figuras cuadriláteras, cuadrado es la que es equilátera y rectangular, rectángulo la que es rectangular pero no equilátera, rombo la que es equilátera pero no rectangular, romboide la que tiene los ángulos y lados opuestos iguales entre sí, pero no es equilátera ni rectangular; y llámense trapecios las demás figuras cuadriláteras.

23. Son rectas paralelas las que estando en el mismo plano y siendo prolongadas indefinidamente en ambos sentidos, no se encuentran una a otra en ninguno de ellos.

POSTULADOS

1. Postúlese el trazar una línea recta desde un punto cualquiera hasta un punto cualquiera.

2. Y el prolongar continuamente una recta finita en línea recta.

3. Y el describir un círculo con cualquier centro y distancia.

4. Y el ser todos los ángulos rectos iguales entre sí.

5. Y que si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente encontrarán en el lado por el que están los (ángulos) menores que dos rectos.

NOCIONES COMUNES

1. Las cosas iguales a una misma cosa son también iguales entre sí.

2. Y si se añaden cosas iguales a cosas iguales, los totales son iguales.

3. Y si de cosas iguales se quitan cosas iguales, los restos son iguales.

4. Y las cosas que coinciden entre sí son iguales entre sí.

5. Y el todo es mayor que la parte.

Con respecto a la geometría, durante prácticamente dos milenios se aceptó la idea de que la geometría contenida en los Elementos, hoy denominada «euclidiana», era la única posible. Sería en el siglo XIX cuando se demostró que el quinto postulado, del que se deduce que «por un punto exterior a una recta sólo se puede trazar otra línea recta en su plano, que pase por el punto y que nunca llegue a encontrarse con la primera línea», no es el único imaginable, siendo posibles otros que dan origen a las que en la actualidad se denominan «geometrías no euclidianas», surgidas de los trabajos de Nicolai Lobachevski (1793-1856), János Bolyai (1802-1860) y Bernhard Riemann (1826-1866).

Independientemente de sus contenidos o del hecho de que sea la primera obra matemática fundamental que ha llegado hasta nosotros, quiero señalar que —y dejando de lado a obras religiosas como la Biblia— los Elementos de Euclides ha sido seguramente el libro de texto que más influencia ha ejercido en la historia de la humanidad. Copiado y editado miles de veces (la primera edición impresa apareció en Venecia —en latín, bajo el título Praeclarissimus liber elementorum Euclides, traducida probablemente del árabe por Alejandro de Bath [c. 1260] y revisada por Giovanni Campano de Novara [c. 1260]— en 1482), hasta hace no muchos años ha formado parte de los textos clásicos de enseñanza de muchas escuelas secundarias a lo largo y ancho del planeta. Y, ya fuese en las aulas o fuera de ellas, la claridad de sus demostraciones dejó su impronta en generaciones y generaciones de jóvenes. Una impronta que sirvió al pensamiento en general, a características tan humanas como son las artes de la expresión, el razonamiento y la comunicación. Y, claro está, también a la ciencia y a los científicos. Y entre éstos a los mejores. Como Bertrand Russell y Albert Einstein, quienes dejaron constancia en sus respectivas autobiografías de lo mucho que debían a Euclides. «A la edad de once años —escribió Russell en el primer volumen de sus memorias—, comencé Euclides, con mi hermano como tutor. Este fue uno de los grandes sucesos de mi vida, tan deslumbrante como el primer amor. No había imaginado que existiese en el mundo algo tan delicioso. Después de haber aprendido la quinta proposición, mi hermano me dijo que esta era considerada generalmente difícil, pero yo no encontré ningún tipo de dificultad. Fue la primera vez que se me ocurrió la idea de que acaso tuviese alguna inteligencia.»

Portada (anotada) de los Elementos de Euclides en griego (Basilea, 1533). Edición preparada por el teólogo protestante Simon Grynaeus, profesor de griego en la Universidad de Basilea.

Primera edición impresa de los Elementos de Euclides: Praeclarissimus liber elementorum Euclides (1482).

Casi a la misma edad, Einstein experimentó una impresión similar, como escribió en su autobiografía (1949):

A la edad de doce años experimenté un segundo asombro de naturaleza muy distinta [el primero fue con una brújula]: fue con un librito sobre geometría euclídea del plano, que cayó en mis manos al comienzo de un curso escolar. Había allí asertos como, por ejemplo, la intersección de las tres alturas de un triángulo en un punto, que, aunque en modo alguno evidentes, podían probarse con tanta seguridad que parecían estar a salvo de toda duda. Esta claridad, esta certeza, ejerció sobre mí una impresión indescriptible. El que hubiera que aceptar los axiomas sin demostración no me inquietaba; para mí era más que suficiente poder construir demostraciones sobre esos postulados cuya validez no se me antojaba dudosa. Recuerdo, por ejemplo, que el teorema de Pitágoras me lo enseñó uno de mis tíos, antes de que el sagrado librito de geometría cayera en mis manos. Tras arduos esfuerzos logré probar el teorema … Solamente necesitaba probar aquello que no me parecía evidente… Esta concepción primitiva, sobre la que seguramente descansa también la famosa cuestión kantiana en torno a la posibilidad de «juicios sintéticos a priori», se basa naturalmente en que la relación entre esos conceptos geométricos y los objetos de la experiencia… estaba allí presente de modo inconsciente. Si bien parecía que a través del pensamiento puro era posible lograr un conocimiento seguro sobre los objetos de la experiencia, el milagro descansaba en un error. Mas para quien lo vive por primera vez, no deja de ser maravilloso que el hombre sea siquiera capaz de lograr, en el pensamiento puro, un grado de certidumbre y pureza como el que los griegos nos mostraron por primera vez en la geometría.

Además de mostrar la atracción que podía ejercer sobre algunos espíritus e inteligencias la estructura y rigor lógico de la matemática euclidiana, el anterior texto de Einstein plantea con claridad el problema de la relación de la matemática con las ciencias naturales, al que ya he aludido. En principio, no parece que sea posible, por muy tentadora que resulte la idea, lograr un conocimiento seguro de los objetos de la experiencia, esto es, de la naturaleza, a través del pensamiento puro, encarnado en estructuras y razonamientos matemáticos. La matemática es, sí, un instrumento universal de conocimiento, pero tiene sus límites.

Sucede, sin embargo, que no todos están de acuerdo sobre cuáles son tales límites. O si existen realmente. Y en este punto es oportuno mencionar al científico británico Paul Dirac (1902-1984), uno de los físicos más destacados del siglo XX (entre sus aportaciones se encuentra una de las formulaciones más fecundas y elegantes de la mecánica cuántica, y la ecuación relativista del electrón, de la que surgió, como consecuencia casi inevitable, la predicción de la existencia de la antimateria). Dirac no compartía totalmente la opinión de Einstein, según la cual es un error pensar que es posible lograr, de manera sistemática, un conocimiento seguro sobre los objetos de la experiencia mediante el pensamiento matemático puro. Para él, en su estudio de los fenómenos naturales el físico tiene dos métodos para progresar: uno, el de experimento y observación, y otro, el de razonamiento matemático. El primero es, escribió en un artículo publicado en 1938-1939 («The relation between mathematics and physics» [«La relación entre matemáticas y física»]), «simplemente la reunión de datos selectos», mientras que el segundo «nos permite inferir resultados de experimentos que no se han realizado». «No existe —añadía— razón lógica por la que el segundo método tenga que ser posible, pero se ha demostrado en la práctica que funciona con notable éxito. Esto debe adscribirse a alguna cualidad matemática en la naturaleza, una cualidad que el observador ocasional de la naturaleza no sospecharía, pero que sin embargo desempeña un importante papel en el esquema de la misma.»

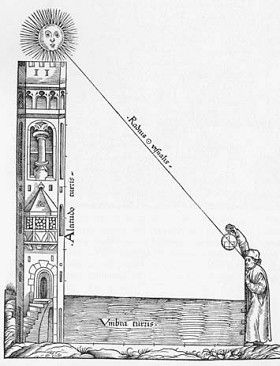
La matemática como ciencia práctica: utilizando la geometría para determinar la altura de una torre. Ilustración tomada de Johannes Stöffler (1452-1531), Elucidatio fabrica ususque astrolabii («Una explicación de la construcción y uso del astrolabio», Tubinga, 1512).

«La matemática y las artes militares», lámina de Walter Ryff, Der mathematischen und mechanischen Künst (Nuremberg, 1547).

«Cualidad matemática en la naturaleza», puede querer decir, claro está, cualquier cosa; por ejemplo que el universo está constituido de tal manera que la matemática es un instrumento útil para describir su estructura. Pero para Dirac semejante manifestación era demasiado trivial. «La conexión entre la matemática y la descripción del universo —señaló— es más profunda que esto… La matemática pura y la física están relacionadas cada vez más estrechamente, aunque sus métodos continúan siendo diferentes. Se puede describir la situación diciendo que el matemático practica un juego en que él mismo inventa las reglas, mientras que el físico practica un juego en el que la naturaleza proporciona las reglas, pero que según transcurre el tiempo se hace cada vez más evidente que las reglas que el matemático encuentra interesantes son las mismas que las que ha escogido la naturaleza. Es difícil predecir cuáles serán los resultados de todo esto. Posiblemente, las dos materias se unificarán en última instancia, teniendo entonces su aplicación física toda rama de la matemática pura, cuya importancia en la física será, por otra parte, proporcional al interés que tenga en la matemática.» Y añadía: «Actualmente, nos encontramos, por supuesto, muy lejos de este nivel, incluso con relación a algunas de las cuestiones más elementales».

Lo que Dirac estaba diciendo es, con otras palabras, que en su opinión en última instancia no es, no será, cierta la creencia generalmente aceptada de que la física se distingue de la matemática porque en aquélla es preciso seleccionar, eliminar, relaciones matemáticas para las que no encontramos correlatos en la naturaleza; la creencia de que las leyes de las ciencias naturales son un subconjunto de las leyes y estructuras matemáticas. Parece que Dirac pensaba —es, ciertamente, un pensamiento arriesgado— que las ciencias de la naturaleza y la matemática coinciden, de alguna manera, realmente, pero que todavía no se han descubierto todos los fenómenos naturales a los que aguarda su estructura matemática.

Pero dejemos estas especulaciones y volvamos al desarrollo histórico de la matemática.

A pesar de todas sus virtudes, novedades y aparente perfección, los Elementos de Euclides no agostaron el universo de los problemas matemáticos. Todo lo contrario: tras esa inmortal obra, la matemática fue haciéndose más poderosa y variada, logrando que el historiador de la ciencia se sienta avergonzado ante la sola idea de intentar resumir su desarrollo. Puedo, no obstante, superar tal vergüenza, en tanto que, lo repito una vez más, lo que yo pretendo en este libro es únicamente resaltar algunas ideas relativas a la ciencia —en este capítulo a la matemática—, en sí misma y en lo que su papel como instrumento de conocimiento se refiere. Citaré, a modo de ejemplo, sin ninguna pretensión de completitud, algunos nombres. Nombres como el de Diofanto de Alejandría (c. 200-284), con quien nació verdaderamente —no importa que, por supuesto, se puedan citar muchos predecesores—, alrededor de 600 años después de Euclides, una ciencia nueva y especialmente importante: el álgebra. En un libro que tituló Arithmetica (escrito, parece, hacia el año 250), Diofanto estudió la resolución exacta de algunas ecuaciones, avanzando, asimismo, en una dirección básica para el álgebra, la de la introducción de abreviaturas (notación algebraica). Todavía hoy llamamos a algunas ecuaciones «diofánticas».

Un nuevo salto, esta vez todavía mayor, de 1.200 años, nos llevaría al Renacimiento, a personajes como Niccolò Tartaglia (c. 1499-1557), que enseñó matemáticas en Verona y Venecia, tradujo Euclides al italiano (la primera traducción que se le hizo a esta lengua) y Arquímedes al latín, descubriendo (1535), entre otras aportaciones, un método que hacía posible resolver ecuaciones cúbicas, método que Girolamo Cardano (1501-1576) divulgó en su Artis magnae, sive de regulis algebraicis, 1545 (El gran arte, sobre las reglas algebraicas), traicionando la confidencia que le había hecho su colega y compatriota.

Pero siendo importantes, imprescindibles realmente, para que la matemática pudiera continuar progresando, aportaciones como las anteriores son menores cuando se comparan con las de tres gigantes del siglo XVII y comienzos del XVIII: René Descartes (1596-1650), Isaac Newton (1642-1727) y Gottfried Wilhelm Leibniz (1646-1716).

Descartes creó la geometría analítica, también denominada «geometría cartesiana», en la que los problemas geométricos pueden traducirse a forma algebraica. Se trataba de un método extremadamente poderoso para resolver problemas geométricos y, a la postre, también dinámicos (el problema del movimiento de los cuerpos), un método que conservamos más de tres siglos después.

En más de un sentido, la contribución de Descartes preparó el camino para el gran descubrimiento de Newton y Leibniz: el del cálculo diferencial (o infinitesimal) e integral, el universo de las derivadas y las integrales; un instrumento incomparable para la indagación matemática y física, al que me referiré de nuevo en el próximo capítulo, dedicado a Newton.

El cálculo infinitesimal a la manera de Leibniz propició la revolución analítica que se introdujo en la matemática europea durante la segunda mitad del siglo XVIII, gracias a los esfuerzos de, especialmente, Leonhard Euler (1707-1783) y Joseph Louis Lagrange (1736-1813). Éste avanzó sustancialmente en la dirección de reducir la mecánica, el estudio de los movimientos, al análisis, en lo que se vendría a denominar mecánica analítica. Se la llamó analítica porque sus principales características eran la manipulación formal de ecuaciones, el empleo de un método formal, o algebraico, esto es, analítico. Frente al enfoque «sintético», visual, newtoniano, los analistas negaban la necesidad de deducciones físicas o geométricas, argumentando que el enfoque intuitivo de la escuela sintética daba lugar a inconsistencias dentro del análisis: así, para llevar una mayor «pureza algebráica» a la teoría de límites, que tantos problemas planteó a Newton, la dotaron de definiciones abstractas libres de cualquier artificio heurístico. Se abrió de esta manera un camino por el que transitaron, entre muchos otros, Carl Friedrich Gauss (1777-1855), SiméonDenis Poisson (1781-1840), Augustin Cauchy (1789-1857), Karl Gustav Jacobi (1804-1851), William Rowan Hamilton (1805-1865) o Henri Poincaré (1854-1912).

Otro avance fundamental, éste ya durante el siglo XIX, es el de la teoría de grupos. Y ahí el nombre más destacado es del francés Évariste Galois (1811-1832), que se dio cuenta de que el problema de desarrollar una teoría general de las ecuaciones algebraicas está regido en cada caso particular por un cierto grupo de sustituciones, en el cual se reflejan las propiedades más importantes de la ecuación considerada. Este descubrimiento, que los sucesores de Galois, y en particular Camille Jordan (1838-1922), esclarecerían y desarrollarían, tiene consecuencias que afectan a un área más vasta de la matemática que la teoría de resolución de ecuaciones. Como señaló en 1895 el gran matemático noruego Sophus Lie (1842-1899): «El gran alcance de la obra de Galois se deriva de este hecho: que su teoría, tan original, de las ecuaciones algebraicas es una aplicación sistemática de dos nociones fundamentales como son la de grupo e invariante… la noción de invariante es evidente en los trabajos de Vandermonde, Lagrange, Gauss, Ampère y Cauchy. Por el contrario, es Galois el primero, me parece, que introdujo la idea de grupo; y en todo caso, él es el primer matemático que ha profundizado en las relaciones existentes entre las ideas de grupo y de invariante». Ideas que en más de un sentido encontraron uno de sus momentos culminantes cuando en 1872, Felix Klein (1849-1925) pronunció su conferencia inaugural como nuevo catedrático de la Universidad de Erlangen. Conferencia que tituló «Consideraciones comparativas sobre las investigaciones geométricas modernas», y que nosotros conocemos como, simplemente, «El programa de Erlangen», en el que definió la geometría de la manera siguiente: «Dado un conjunto de cualquier número de dimensiones, y un grupo de transformaciones entre sus elementos, se llama geometría al estudio de las propiedades de aquel conjunto que son invariantes respecto de las transformaciones de este grupo». De esta forma, el estudio de la geometría se reducía al de todos los grupos de transformación imaginables, que son, por supuesto, infinitos.

Es difícil apreciar el extraordinario papel que, desde que fueron introducidas y sistematizadas, ha desempeñado en la ciencia —en la matemática y en la física, especialmente— la teoría de grupos, así como la noción de invariancia y la, estrechamente ligada a ella, de simetría (en matemática se dice que existe una simetría cuando un conjunto determinado mantiene su configuración al ser sometido a una cierta transformación).

La idea de simetría es particularmente atractiva. Nos indica una cualidad o propiedad común, constante, que subyace detrás de las apariencias. En tanto que uno de los objetivos preferentes de la ciencia es precisamente identificar regularidades (acaso sea el único objetivo real, puesto ¿qué es una ley científica sino la expresión de una regularidad, de algo que se conserva?), es natural que los científicos reciban con especial agrado a cualquier simetría.

El primer principio de simetría importante conscientemente descubierto en la física fundamental fue la invariancia (o simetría) de Lorentz. En este proceso la invariancia fue un descubrimiento secundario, pero Hermann Minkowski se encargó enseguida de dar la vuelta al procedimiento, requiriendo que las ecuaciones fuesen invariantes. Einstein quedó tan impresionado con las poderosas consecuencias físicas de los principios de simetría que trabajó para ampliar la invariancia de Lorentz, lo que le llevó, junto al principio de equivalencia, a la teoría de la relatividad general. Se puede decir, por consiguiente, que Einstein inició el principio —o el «movimiento»— de que la simetría dicta las interacciones, una idea que desempeñó un papel esencial en la física teórica del siglo XX.

Una de las luces, en efecto, que han iluminado la investigación teórica en la física de altas energías se encuentra en los principios de simetría (de todo tipo, como la simetría partícula-antipartícula, y no únicamente clásicos como la homogeneidad espacial o temporal). Steven Weinberg (1933-), uno de los físicos teóricos más destacados de la segunda mitad del siglo XX ha escrito en este sentido: «Cada vez está más claro que el grupo de simetría de la naturaleza es la cosa más profunda que podemos entender en la actualidad sobre la naturaleza. Me gustaría sugerir aquí algo de lo que no estoy realmente seguro pero que es al menos una posibilidad: que especificar el grupo de simetría de la naturaleza puede ser todo lo que necesitemos decir acerca del mundo físico, más allá de los principios de la mecánica cuántica».

Desde este punto de vista, al nivel más profundo todo lo que existiría serían simetrías y respuestas a simetrías. La propia materia se disuelve y el universo se nos aparece como una gran representación de conjuntos (técnicamente grupos) de simetrías.

Claro que también es posible defender ideas en principio opuestas. Animado por los resultados a los que llegaba en sus estudios sobre la relación existente entre actividad óptica, estructura cristalina y la composición química de compuestos orgánicos (el ácido tartárico en especial), Louis Pasteur escribió en 1874 que el «universo es una estructura asimétrica y estoy convencido de que la vida, tal y como nosotros la conocemos, es un resultado directo de la asimetría del universo o de las consecuencias que ello entraña».

De hecho, la física de los últimos tiempos ha desarrollado un concepto que se amolda bastante bien a la idea de Pasteur. Me refiero al concepto de ruptura de simetría, cuya introducción en la física teórica ha sido comparada con la «demolición» de las esferas celestes realizada por Copérnico y Kepler.

Expuesto de una manera elemental, las rupturas de simetrías son procesos mediante los cuales, en determinadas circunstancias o en momentos concretos de la historia del universo, las simetrías que hasta entonces se verificaban se rompen, dando origen a nuevos fenómenos o fuerzas. El ejemplo paradigmático en este sentido es el de las interacciones. En la actualidad vemos cuatro fuerzas diferentes, pero en el comienzo y primeros instantes de vida del universo habría existido una única fuerza; al irse expandiendo y en consecuencia enfriando el universo, se habría ido «desintegrando» aquella fuerza en las cuatro que conocemos. La física teórica dispone desde hace tiempo de teorías en las que tres de las cuatro fuerzas han sido unificadas en el sentido anterior. Primero se desarrolló (Steven Weinberg y Abdus Salam [1967-1968] con aportaciones de otros físicos, Sheldon Glashow en particular) la teoría electrodébil, que unificaba la interacción débil y la electromagnética; más tarde vino la denominada teoría estándar, que incluía también a la interacción fuerte. Todavía no se ha resuelto el problema de la gran unificación, que tenga en cuenta también la fuerza gravitacional, aunque existen teorías candidatas, como la de supercuerdas. Otros procesos de ruptura espontánea de simetrías especialmente importantes son aquellos que contribuyen a explicar (mediante un mecanismo denominado de Anderson-Higgs) las diversas masas de las partículas que aparecen en el modelo estándar.

Regresando a la idea de Pasteur, tendríamos que en cierto sentido habría tenido razón: parece inevitable aceptar que la vida, en cualquiera de sus formas, sólo es posible cuando existen regiones en las que la temperatura no es excesivamente alta. Pero ha sido precisamente el enfriamiento cósmico el responsable de la ruptura de la gran simetría que imperó en los primeros instantes del universo. En este, restringido, sentido vida y asimetría aparecen como distintos aspectos de una misma realidad.

Aunque no es una caracterización completamente correcta (pensemos, por ejemplo, en la topología, que se ocupa de, por decirlo de alguna forma, relaciones), la matemática tiene mucho que ver con la cuantificación. Ahora bien, en principio parece que sólo se puede cuantificar aquello que es finito, no lo infinito. Sin embargo, esta idea es errónea, aunque llevó mucho tiempo a los matemáticos comprender bien el sentido de tal error, lo que no quiere decir, de todas maneras, que la noción de «infinito» no figurase entre sus constructos.

En efecto, ya en la primera mitad del siglo VII, el astrónomo indio Brahmagupta (598-670), definió el infinito como el número cuyo denominador es cero; se utiliza para él el símbolo ∞ (introducido, parece, por el matemático inglés John Wallis [1616-1703] en 1655).

Aunque en una discusión más completa no podría olvidarse a Bernardus Bolzano (1781-1848), autor de un tratado (publicado póstumamente en 1850, sobre Paradoxien des Unendlichen (Paradojas del infinito), fue realmente Georg Cantor (1845-1918) quien, a finales del siglo XIX, se dio cuenta de que hay, por expresarlo de alguna forma, muchos infinitos, sentando así las bases de la teoría de los conjuntos y de los números transfinitos. La idea que subyace en esta nueva matemática es la de contar los elementos de dos conjuntos poniéndolos en correspondencia, uno a uno, sin repetición ni omisión. De esta manera, es inmediato ver que hay igual cantidad de números naturales (1, 2, 3, 4…) que de números pares o impares. Asimismo, todo segmento de una recta contiene el mismo número —infinito— de puntos que cualquier otro segmento de una línea recta; también —fue el primer descubrimiento revolucionario de Cantor— hay tantos puntos en todo el plano como en una recta. Ocurre, sin embargo, que estos últimos infinitos no son de la misma naturaleza que el infinito de los números enteros (… −3, –2, –1, 0, 1, 2, 3…): es el infinito de los números irracionales (aquellos que no se pueden expresar como cociente de dos enteros). Nos vemos conducidos así a hablar de «números cardinales», el número de elementos que tiene un conjunto: para conjuntos finitos, su número cardinal (o «potencia») es el número usual de sus elementos, mientras que para conjuntos infinitos es preciso introducir nuevos términos; Cantor utilizó la primera letra del alfabeto hebreo, «aleph», seguida del subíndice cero —ℵ₀—, para denotar el número cardinal del conjunto de los naturales.

Este número tiene propiedades que desde la lógica habitual, aristotélica, parecen paradójicas:

A cualquier conjunto cuyos elementos se pueden poner en correspondencia uno-a-uno con el conjunto de los naturales, Cantor lo denominó «numerable». Ya he indicado que los números pares y los impares son numerables, pero es posible demostrar que también lo es el conjunto de los enteros. Lo mismo sucede con los racionales. Un número racional p/q se define mediante una pareja —(p, q)— de enteros, por tanto la cantidad de racionales será ℵ₀², pero esto es igual, recordemos, a ℵ₀.

Sin embargo, no ocurre otro tanto con los números reales (que podemos considerar como números decimales con una cantidad ilimitada de cifras decimales). La demostración de que hay más números reales que enteros o naturales no es inmediata, pero Cantor logró probarlo, y asignó a ese nuevo número cardinal la letra c.

Se trataba, obviamente, de un mundo completamente nuevo. Un mundo sorprendente para las categorías habituales dentro de la lógica tradicional de lo finito, un mundo que condujo al descubrimiento de nuevos y fecundos continentes matemáticos, como el de la «teoría de conjuntos», que se instaló de manera profunda en el cuerpo de la matemática del siglo XX.

De una forma un tanto general, pero no por ello menos real, se puede decir de ese siglo XIX, y más aún de su segunda mitad, en el que se descubrieron todas las posibilidades que escondía el concepto de infinito, que fue una época extraordinariamente fructífera para la matemática, no importa que en ella se sembraran las semillas que al germinar mostraron que algunas de las esperanzas que había generado eran infundadas. Y es que lo verdaderamente importante en ciencia no es que se cumplan nuestras expectativas, sino descubrir aquello que «realmente es»; esto es, encontrar la Verdad. Una verdad que con frecuencia suele entrar en conflicto con nuestras ideas más firmemente establecidas.

En todos estos aspectos, al igual que en lo que se refiere al desarrollo más tradicional de la matemática, el siglo XIX fue, ya digo, extraordinario, haciendo que asome una sonrisa en nuestros rostros cuando recordamos manifestaciones como la que realizó Denis Diderot («L’interprétation de la nature» [«La interpretación de la naturaleza»]) en el siglo XVIII:

Nos encontramos en medio de una gran revolución en las ciencias. Las formas en que se están estudiando en la actualidad la ética, literatura, historia natural y física experimental me convencen de que antes de que hayan pasado otros cien años, no será ya posible encontrar tres grandes matemáticos [géomètres] en Europa. Se producirá en esta ciencia un abrupto alto y permanecerá allí donde los Bernoullis, los Eulers, los Maupertuises, los Clairauts, los Fontaines y los d’Alemberts la dejaron… En los años venideros sus trabajos se mantendrán como las pirámides de Egipto, combinaciones de enormes masas y densos jeroglíficos que nos inspiran un aterrador sentimiento del poder y recursos de los hombres que las construyeron.

El camino de generalización abierto por matemáticos como Galois y Cantor continuaría, cada vez con fuerza creciente. En 1899, en el umbral del nuevo siglo, David Hilbert (1862-1943), publicaba un libro, Grundlagen der Geometrie (Fundamentos de la geometría), en el que axiomatizaba de manera completa la geometría, demostrando así su carácter puramente formal, carácter que ya habían adquirido el álgebra y el análisis. Al hacer hincapié en que incluso en una rama de las matemáticas tan aparentemente empírica como la geometría se podía eliminar el nivel intuitivo-empírico, Hilbert se convirtió en el principal exponente de una de las tres corrientes que caracterizaron a la investigación matemática de las primeras décadas del siglo XX: el formalismo, o escuela axiomática, que compartió protagonismo con otras dos, el intuicionismo, asociada al nombre del holandés Luitzen Brouwer (1881-1967), y el logicismo, cuya manifestación más señalada son los tres tomos de Bertrand Russell y Alfred North Whitehead (1861-1947), Principia Mathematica (1910, 1912, 1913). En esta obra sus autores pretendían demostrar que toda la matemática se puede basar en la lógica; esto es, que los conceptos de todas las teorías matemáticas, al igual que los métodos de prueba e inferencia, se podrían formular dentro del contexto de la lógica (señalemos que para Russell lógica y aritmética estaban estrechamente ligadas: «La transición de la lógica a la aritmética —escribió en un ensayo titulado “Is mathematics purely linguistic?” [“¿Es la matemática puramente lingüística?”, 1950 o 1951]— es tan gradual que nadie puede decir dónde termina una y comienza la otra, así que estamos obligados a considerar la lógica matemática y la aritmética como una sola materia»).

Desgraciadamente, ni siquiera en el reino de la matemática se cumplen pretensiones tan aparentemente racionales. A pesar de los logros innegables alcanzados en Principia Mathematica, a la postre no logró alcanzar su meta. El propio Russell comenzó, algunos años más tarde, a dar señales de que su fe reduccionista disminuía; él, que tan apasionadamente había defendido la visión logicista y apriorística de la matemática, pasó a sostener la tesis opuesta, empirista, según la cual la matemática no era diferente a, por ejemplo, las ecuaciones de Maxwell del electromagnetismo: «ambas —manifestó en 1924— se aceptan debido a que se observa que algunas de sus consecuencias lógicas son ciertas».

La respuesta negativa a las esperanzas de los logicistas —y también de los formalistas— sorprendería, creo yo, tanto a ellos como a los intuicionistas. Y lo hizo porque fue inesperada. Para comprender su novedad me detendré un momento en uno de esos momentos históricos que se dan de vez en cuando en las actividades humanas, sean científicas o no: la conferencia que pronunció David Hilbert (un formalista, recordemos, no un logicista) en el Segundo Congreso Internacional de Matemáticos, celebrado en París, del 6 al 12 de agosto de 1900. Su título, «Mathematische Probleme», aunque habitualmente es citada como «Sobre los problemas futuros de las matemáticas».

David Hilbert en 1912, en una de las postales de profesores que se vendían en Gotinga.

Los pasajes que me interesan no se encuentran en ninguno de los célebres 23 problemas que Hilbert trató en aquella ocasión, sino en la parte introductoria. Recordaba allí el catedrático de Gotinga que los «antiguos nos dieron los primeros ejemplos de… demostraciones de imposibilidad», demostraciones como la de que en un triángulo rectángulo isósceles la hipotenusa y el lado del ángulo recto se encuentran en una relación irracional. Señalaba, asimismo, que en «la matemática moderna, la cuestión de la imposibilidad de ciertas soluciones desempeña un papel preponderante», haciendo posible resolver antiguos y difíciles problemas, tales como la demostración del axioma de las paralelas, la cuadratura del círculo y la resolución mediante radicales de la ecuación de quinto grado, «aunque en un sentido completamente diferente al que se buscaba primitivamente», al mostrar su imposibilidad.

De estos resultados, que habían desafiado a los matemáticos durante siglos, surgió la convicción que, señalaba Hilbert, «compartirá ciertamente todo matemático, pero de la que hasta el momento nadie ha construido prueba alguna… de que todo problema matemático determinado debe ser a la fuerza susceptible de una solución rigurosa, ya sea mediante una respuesta directa de la cuestión planteada, o bien demostrando la imposibilidad de la solución». Y en este punto, añadía: «¿Es este axioma de la posibilidad de resolver todo problema una propiedad característica y distintiva del pensamiento matemático, o será acaso una ley general del modo de existencia de nuestro entendimiento; a saber, que todas las cuestiones que se plantea nuestro entendimiento son susceptibles de ser resueltas por él?».

Lo que seguramente Hilbert tenía en mente era que no se había podido demostrar que todo problema matemático, toda formulación o proposición matemática, pudiese ser resuelta en el sentido afirmativo o negativo, pero yo no dudo de que él estaba convencido que sería posible demostrar lo uno o lo otro. Sin embargo, resultó que no fue, que no es, eso, ni lo uno ni lo otro, aunque si somos cuidadosos al leer la manifestación de Hilbert, veremos que el desarrollo al que me voy a referir no negaba —todo lo contrario, reafirmaba— que «todas las cuestiones que se plantea nuestro entendimiento son susceptibles de ser resueltas por él».

Ese desarrollo, que alteró profunda, dramáticamente, las creencias más firmemente establecidas en el pensamiento científico (no sólo matemático), constituyendo en más de un sentido el golpe de gracia para la matemática como sistema inductivo-empírico o apriorístico, para el programa logicista al igual que para el formalista (que insistía en la necesidad de axiomatizar la lógica, en un sistema formal no contradictorio), vino de la mano de un lógico nacido en Brünn, Moravia, que murió, envuelto en las grises y amargas nieblas de la demencia, al otro lado del Atlántico, en Princeton, cuyo Institute for Advanced Study le había acogido en 1939. Se llamaba Kurt Gödel (1906-1978).

En 1931 se publicó el artículo más famoso de Gödel y quizá de toda la historia de la lógica: «Über formal unentscheidbare Sätze der Principia mathematica und verwandter System» («Sobre sentencias formalmente indecidibles de Principia Mathematica y sistemas afines»). En él se demostraba, en primer lugar, que todos los sistemas formales de la matemática clásica son incompletos, es decir, que para cada uno de ellos puede construirse una sentencia indecidible (tal que ni ella ni su negación es deducible), y que esta incompletitud es inevitable (por muchos axiomas que añadamos, los sistemas formales siguen siendo incompletos). En segundo lugar, Gödel mostró que es imposible probar la consistencia de un sistema formal de la matemática clásica. En otras palabras, demostró que no es posible lograr un reduccionismo completo en los sistemas matemáticos, ya que existen sentencias de las que no podemos saber si son o no ciertas, y sistemas cuya consistencia no es posible verificar.

Los resultados de Gödel producen, a mí al menos, una gran admiración por la creatividad de su autor, pero también una profunda sensación de desamparo. Ya ni siquiera es posible encontrar seguridad en el único lugar donde creíamos que existía, en la matemática. Claro que tal vez ese mismo resultado se pueda interpretar como algo que humaniza a la matemática, que nos permite dejar abierta la puerta para justificar la incertidumbre y el compromiso ante la imposibilidad de encontrar una respuesta incontrovertible.

Por otra parte, lo que sobre todo muestra el resultado de Gödel es que, cito la expresión hilbertiana por tercera vez: «todas las cuestiones que se plantea nuestro entendimiento son susceptibles de ser resueltas por él». El propio Gödel era de esta opinión. En una carta que dirigió a David Plummer el 31 de julio de 1967, manifestaba que había construido sus teoremas de incompletitud no para establecer limitaciones en el poder del razonamiento humano, sino más bien para demostrar «que la clase de razonamiento necesario en matemáticas no puede ser mecanizado completamente», reafirmando de esta forma el papel del intelecto humano en la investigación matemática. Debido a su creencia en que la mente humana no «es estática, sino que se desarrolla constantemente», tenía confianza en que continuarían apareciendo nuevas ideas matemáticas. Son, en este sentido, reveladoras las siguientes manifestaciones, incluidas en un suplemento que añadió en 1964 a un artículo titulado «What is Cantor’s continuum problem?» («¿Cuál es el problema del continuo de Cantor?»), publicado inicialmente en 1947: «Pero, a pesar de lo remotos que se encuentran de la experiencia sensorial, nosotros poseemos algo así como una percepción también de los objetos de la teoría de conjuntos, como se ve del hecho de que la verdad de los propios axiomas se nos hace evidente. No veo ninguna razón de por qué debamos tener menos confianza en este tipo de percepción, esto es, en la intuición matemática, que en la percepción sensorial, que nos induce a construir teorías físicas y a esperar que futuras percepciones sensoriales estén de acuerdo con ellas, y, más aún, a creer que una cuestión no decidible ahora tiene sentido y puede ser decidida en el futuro».

Howard P. Robertson, Eugene Wigner, Hermann Weyl, Kurt Gödel, Isidor Rabi, Albert Einstein, Rudolf Ladenburg, Robert Oppenheimer y G. M. Clemence, en el Institute for Advanced Study de Princeton en 1949.

Ideas muy similares expresó hace unos años el físico y matemático británico Roger Penrose en un libro titulado The Emperor’s New Mind (La nueva mente del emperador; 1989). En él, Penrose defendía la idea de que existen enunciados que podemos ver que son seguros, aunque como consecuencia de los resultados obtenidos por Gödel en 1931 no podamos asignarles la categoría de «verdaderos». Y de ahí concluía, platónicamente, que «la noción de verdad matemática va más allá del concepto global de formalismo. Hay algo absoluto e “infuso” en la verdad matemática… [que] va más allá de las simples construcciones humanas». Palabras estas que recuerdan a otras que escribió Arthur Schopenhauer (1788-1860) en uno de sus manuscritos berlineses: «Cada cual sólo conoce de verdad aquello que ha captado intuitivamente, lo que sabe in abstracto supone una simple asignación al saldo de su conocimiento intuitivo».

En cualquier caso, los resultados de Gödel, esa pérdida, aparente al menos, de certidumbre que revelan, no ha impedido que continúe progresando la investigación matemática. Muestra de semejante progreso es, por ejemplo, el descubrimiento de los denominados objetos fractales, entes geométricos que pueden tener dimensiones «intermedias», como 3/2 o logaritmo neperiano de 2 dividido por logaritmo neperiano de 3, algo realmente extraordinario teniendo en cuenta que estamos acostumbrados a entes geométricos de dimensión 3 (volúmenes), 2 (áreas), 1 (líneas) o 0 (puntos). Estos nuevos objetos, junto a otros como los sistemas (no lineales) caóticos (aquellos que dependen fuertemente de las condiciones iniciales), o la irresistible introducción de los ordenadores, prometen un futuro abierto para la matemática, desde luego, y, con su ayuda, también para otras disciplinas científicas. Sin olvidar el que ha sido posible, finalmente, resolver viejos problemas que tenía planteada la matemática. Así ha ocurrido, en efecto, con una conjetura que el matemático y jurista francés Pierre de Fermat (1601-1665) propuso en 1637, en el margen de su ejemplar del Libro II de la Arithmetica de Diofanto; el denominado «Último teorema de Fermat», que afirma que si n es un entero mayor que 2, la ecuación xn + yn = zn no tiene solución si x, y, z son enteros positivos. Fue en septiembre de 1994, cuando el matemático británico, afincado en Princeton, Andrew Wiles (1953), logró demostrar definitivamente la conjetura de Shimura-Taniyama-Weil, que implicaba la verificación del teorema de Fermat.

1 La matemática, instrumento universal de conocimiento: de Euclides a Gödel

1
La matemática, instrumento universal de conocimiento: de Euclides a Gödel