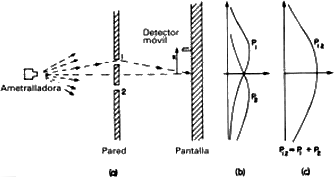
6.1 Experimento de interferencia con balas.
Para tratar de entender el comportamiento cuántico de los electrones, compararemos y contrastaremos su comportamiento, en un montaje experimental concreto, con el comportamiento más familiar de partículas tales como balas y con el comportamiento de ondas tales como las ondas de agua. Consideremos primero el comportamiento de las balas en el montaje experimental mostrado esquemáticamente en la figura 6.1. Tenemos una ametralladora que dispara un chorro de balas. No es una ametralladora muy buena, pues las balas se dispersan (aleatoriamente) sobre una extensión angular bastante grande, tal como se indica en la figura. Frente a la ametralladora tenemos una pared (constituida por una lámina acorazada) que tiene dos agujeros del tamaño suficiente para permitir el paso de una bala. Detrás de la pared hay una pantalla (digamos una pared gruesa de madera) que «absorberá» las balas cuando incidan en ella. Delante de la pantalla tenemos un objeto que llamaremos un «detector» de balas. Podría ser una caja que contenga arena. Cualquier bala que entre en el detector quedara frenada y almacenada. Cuando lo deseemos, podemos vaciar la caja y contar el número de balas que han sido recogidas. El detector puede moverse de un lado a otro (en lo que denominaremos la dirección x).

6.1 Experimento de interferencia con balas.
Con este aparato podemos encontrar experimentalmente la respuesta a la pregunta: «¿Cuál es la probabilidad de que una bala que pasa a través de los agujeros de la pared llegue a un punto de la pantalla situado a una distancia x del centro?». En primer lugar, ustedes deben darse cuenta de que tenemos que hablar de probabilidad, porque no podemos decir categóricamente dónde irá a parar cada bala concreta. Una bala que incida por casualidad en uno de los agujeros puede rebotar en los bordes del mismo y terminar en cualquier parte. Por «probabilidad» entendemos las posibilidades de que la bala llegue al detector, que podemos medir contando el número de balas que llegan al detector en un intervalo de tiempo dado y tomando luego el cociente entre este número y el número total de balas que inciden en la pantalla durante este tiempo. O, si suponemos que la ametralladora dispara siempre al mismo ritmo durante las medidas, la probabilidad que buscamos es simplemente proporcional al número de balas que llegan al detector en un intervalo de tiempo estándar.
Para nuestros propósitos actuales nos gustaría imaginar un experimento algo idealizado en el que las balas no son balas reales, sino que son balas indestructibles, que no pueden partirse en dos. En nuestro experimento encontramos que las balas siempre llegan en porciones, y cuando encontramos algo en el detector, se trata siempre de una bala entera. Si el ritmo al que dispara la ametralladora se hace muy lento, encontramos que en cualquier instante dado o bien no llega nada o bien llega una y sólo una exactamente una bala a la pantalla. Además, el tamaño de la porción no depende del ritmo de disparo de la ametralladora. Diremos: «Las balas llegan siempre en porciones idénticas». Lo que medimos con nuestro detector es la probabilidad de llegada de una porción. Y medimos la probabilidad como una función de x. El resultado de tales medidas con este aparato (aún no hemos hecho el experimento, de modo que en realidad estamos imaginando el resultado) se representa en la gráfica dibujada en la parte (c) de la figura 6.1. En la gráfica representamos la probabilidad hacia la derecha y x en vertical, de modo que la escala x se ajusta al diagrama del aparato. Llamaremos a esta probabilidad P12 porque las balas pueden haber atravesado el agujero 1 o el agujero 2. Ustedes no se sorprenderán de que P12 sea alta cerca del centro de la gráfica y se haga pequeña si x es muy grande. Ustedes pueden preguntarse, sin embargo, por qué P12 tiene su valor máximo en x = 0. Podemos entender este hecho si repetimos nuestro experimento después de tapar el agujero 2 y lo volvemos a repetir mientras está tapado el agujero 1. Cuando el agujero 2 está tapado, las balas sólo pueden pasar a través del agujero 1, y obtenemos la curva marcada P1 en la parte (b) de la figura. Como ustedes esperarían, el máximo de P1 ocurre en el valor de x que está alineado con la ametralladora y el agujero 1. Cuando el agujero 1 está cerrado, obtenemos la curva simétrica P2 dibujada en la figura. P2 es la distribución de probabilidad para las balas que pasan a través del agujero 2. Comparando las partes (b) y (c) de la figura 6.1, encontramos el importante resultado de que
P12= P1+ P2 (6.2)
Las probabilidades simplemente se suman. El efecto cuando ambos agujeros están abiertos es la suma de los efectos con cada agujero abierto por separado. Llamaremos a este resultado una observación de «ausencia de interferencia», por una razón que verán más adelante. Hasta aquí lo relativo a las balas. Ellas llegan en porciones, y su probabilidad de llegada no muestra interferencia.