
4.3 Máquina simple para levantar pesos.
La conservación de la energía sólo puede entenderse si disponemos de las fórmulas para todas sus formas. Quiero discutir la fórmula para la energía gravitatoria cerca de la superficie de la Tierra, y quiero derivar esta fórmula de una manera que no tiene nada que ver con la historia, sino que es simplemente una línea de razonamiento concebida para esta lección concreta a fin de ofrecerles una ilustración del hecho notable de que muchas cosas acerca de la naturaleza pueden extraerse de unos pocos hechos y por razonamiento riguroso. Es una ilustración del tipo de trabajo en que se ven envueltos los físicos teóricos. Está estructurado siguiendo un excelente razonamiento del señor Carnot sobre la eficiencia de las máquinas de vapor[3].
Consideremos máquinas para levantar pesos: máquinas que tienen la propiedad de que levantan un peso mediante el descenso de un segundo peso. Hagamos también una hipótesis: que no hay nada semejante a un movimiento perpetuo en estas máquinas de levantar pesos. (De hecho, el que no hay movimiento perpetuo en absoluto es un enunciado general de la ley de la conservación de la energía). Debemos tener cuidado al definir el movimiento perpetuo. Hagámoslo, en primer lugar, para las máquinas de levantar pesos. Si, una vez que hemos elevado y bajado muchos pesos y restituido la máquina a la condición original, encontramos que el resultado neto consiste en haber levantado un peso, entonces tenemos una máquina de movimiento perpetuo porque podemos utilizar dicho peso levantado para mover alguna otra cosa. Esto es, siempre y cuando la máquina que levantó el peso sea devuelta a su condición original exacta, y que además sea completamente autocontenida: que no haya recibido la energía para levantar el peso de alguna fuente externa, como los bloques de Bruce.
Una máquina de levantar pesos muy sencilla se muestra en la figura 4.3. Esta máquina levanta pesos de tres unidades de «fuerza». Colocamos tres unidades en un plato de una balanza, y una unidad en el otro plato. Sin embargo, para hacer que realmente funcione debemos quitar un peso pequeño del plato izquierdo. Recíprocamente, podríamos levantar un peso de una unidad bajando un peso de tres unidades si hacemos una pequeña trampa quitando un pequeño peso del otro plato. Por supuesto, nos damos cuenta de que en cualquier máquina de levantar pesos real debemos añadir algo extra para hacerla funcionar. Pasaremos esto por alto, por el momento. Las máquinas ideales, aunque no existen, no requieren nada extra. Una máquina que realmente usamos puede ser, en cierto modo, casi reversible: es decir, si levantásemos un peso de tres bajando un peso de uno, entonces también levantaríamos la misma altura el peso de uno bajando el peso de tres.

4.3 Máquina simple para levantar pesos.
Imaginemos que hay dos clases de máquinas, las que no son reversibles, que incluyen todas las máquinas reales, y las que son reversibles, que por supuesto no son realmente alcanzables por muy cuidadosos que seamos en nuestro diseño de los engranajes, brazos, etc. Supondremos, sin embargo, que existe tal cosa una máquina reversible que hace descender una unidad de peso (un kilo o cualquier otra unidad) una unidad de distancia, y al mismo tiempo levanta un peso de tres unidades. Llamemos Máquina A a esta máquina reversible. Supongamos que esta máquina reversible particular levanta el peso de tres unidades una distancia X. Supongamos además que tenemos otra máquina, la Máquina B, que no es necesariamente reversible, que también hace descender un peso unidad una unidad de distancia pero que eleva tres unidades de peso a una distancia Y. Podemos ahora probar que Y no está más alto que X; es decir, es imposible construir una máquina que levante un peso a una altura mayor que la que sería levantado por una máquina reversible. Veamos por qué. Supongamos que Y fuera mayor que X. Tomemos un peso de una unidad y hagámoslo descender una altura unidad con la Máquina B, lo que hace que se eleve el peso de tres unidades a una distancia Y. Entonces podríamos bajar el peso desde Y hasta X, obteniendo potencia libre, y utilizar luego la Máquina A reversible, funcionando al revés, para hacer descender el peso de tres unidades una distancia X y elevar el peso de una unidad a una altura unidad. ¡Esto volvería a situar el peso de una unidad donde estaba antes, y dejaría ambas máquinas listas para ser utilizadas de nuevo! Tendríamos entonces movimiento perpetuo si Y estuviera más alto que X, pero habíamos supuesto que el movimiento perpetuo era imposible. Con estas hipótesis deducimos que Y no está más alto que X, de modo que, de todas las máquinas que pueden ser diseñadas, la máquina reversible es la mejor.
Podemos ver también que todas las máquinas reversibles deben levantar el peso exactamente a la misma altura. Supongamos que B fuese también realmente reversible. El argumento de que Y no está más alto que X sigue siendo, por supuesto, igual de bueno que lo era antes, pero también podemos seguir nuestro argumento al revés, utilizando las máquinas en el orden contrario, y probar que X no está más alto que Y. Esta es una observación muy notable porque nos permite analizar la altura a la que diferentes máquinas van a levantar algo sin mirar el mecanismo interior. Inmediatamente sabemos que si alguien construye un sistema de palancas enormemente elaborado que levanta tres unidades de peso una cierta distancia al tiempo que hace descender una unidad de peso en una distancia unidad, y lo comparamos con una balanza simple que hace lo mismo y es fundamentalmente reversible, su máquina no levantará más alto, sino probablemente a menos altura. Si su máquina es reversible, sabemos también exactamente a qué altura levantará. Para resumir: cualquier máquina reversible, independientemente de cómo opere, que baja un kilogramo un metro y con ello eleva un peso de tres kilogramos, lo eleva siempre la misma distancia, X. Esta es evidentemente una ley universal de gran utilidad. La siguiente pregunta es, por supuesto, ¿cuánto vale X?
4.4 Una máquina reversible.
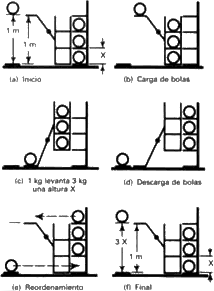
Supongamos que tenemos una máquina reversible que va a levantar esta distancia X, con la misma proporción de pesos tres a uno. Coloquemos tres bolas en una estantería fija, como se muestra en la figura 4.4. Una bola se mantiene en una plataforma a una distancia de un metro sobre el nivel del suelo. La máquina puede levantar tres bolas, haciendo descender una bola una distancia 1. Ahora bien, hemos dispuesto que la estantería móvil que sostiene las tres bolas tiene un suelo y dos baldas más, exactamente espaciadas una distancia X, y, además, que las baldas de la estantería fija también están espaciadas una distancia X, (a). En primer lugar hacemos rodar las bolas horizontalmente desde la estantería fija a las baldas de la estantería móvil, (b), y supongamos que esto no necesita energía porque no cambiamos la altura. Entonces entra en acción la máquina reversible: baja la bola individual al suelo y levanta la estantería móvil una distancia X, (c). La estantería móvil está dispuesta ingeniosamente de modo que dichas bolas están de nuevo niveladas con las baldas fijas. Entonces descargamos las bolas de la estantería móvil en la fija, (d); habiendo descargado las bolas, podemos devolver la máquina a su situación original. Ahora tenemos tres bolas en las tres baldas superiores y una bola en el suelo. Pero lo curioso es que, en cierto modo, no hemos levantado dos de ellas en absoluto porque, después de todo, antes ya había bolas en las baldas 2 y 3. El efecto neto resultante ha sido el de levantar una bola a una distancia 3X. Ahora bien, si 3X excediera de un metro, podríamos bajar la bola para devolver la máquina a la situación inicial, (f), y podríamos volver a poner en marcha el aparato. Por lo tanto, 3X no puede ser mayor que un metro, pues si lo fuera podríamos tener movimiento perpetuo. Análogamente, podemos probar que un metro no puede ser mayor que 3X haciendo que toda la máquina funcione al revés, puesto que es una máquina reversible. Por lo tanto, 3X no es ni mayor ni menor que un metro, y descubrimos así, mediante puro razonamiento, la ley según la cual X = 1/3 de metro. La generalización es clara: un kilogramo desciende una cierta distancia al operar una máquina reversible; luego la máquina puede elevar p kilogramos a esta misma distancia dividida por p. Otra forma de poner el resultado es que tres kilogramos multiplicado por la altura elevada, que en nuestro problema era X, es igual a un kilogramo multiplicado por la distancia descendida, que es un metro en este caso. Si tomamos todos los pesos y los multiplicamos por las alturas a las que están inicialmente sobre el nivel del suelo, dejamos operar la máquina, y luego volvemos a multiplicar todos los pesos por todas las nuevas alturas, no habrá cambio. (Tenemos que generalizar el ejemplo en el que movíamos sólo un peso al caso en el que, cuando bajamos uno, elevamos varios pesos diferentes, pero esto es fácil).
La suma de los productos de los pesos por sus alturas se denomina energía potencial gravitatoria: es la energía que tiene un objeto debido a su posición en el espacio con respecto a la Tierra. Así, la fórmula para la energía gravitatoria, siempre que no estemos demasiado lejos de la Tierra (la fuerza se debilita a medida que subimos más alto) es
Energía potencial gravitatoria de un objeto = peso × altura (4.5)
Esta es una bella línea de razonamiento. El único problema es que quizá no sea verdadera. (Después de todo, la naturaleza no tiene que ir a la par con nuestro razonamiento). Por ejemplo, quizá el movimiento perpetuo sea de hecho posible. Algunas de las hipótesis pueden ser falsas, o quizá hayamos cometido un error en el razonamiento, de modo que siempre es necesario comprobarlo. De hecho, experimentalmente resulta ser verdadero.
El nombre genérico de la energía que tiene que ver con la posición con respecto a alguna otra cosa se denomina energía potencial. En este caso particular, por supuesto, la llamamos energía potencial gravitatoria. Si en lugar de trabajar contra fuerzas gravitatorias es contra fuerzas eléctricas contra las que estamos trabajando, si estamos «elevando» cargas alejándolas de otras cargas mediante un montón de palancas, entonces la energía contenida se denomina energía potencial eléctrica. El principio general es que el cambio en la energía es la fuerza multiplicada por la distancia que se desplaza dicha fuerza; en general
Cambio en energía = fuerza × distancia a lo largo de la que actúa la fuerza (4.6)
Volveremos a muchos de estos otros tipos de energía a medida que avancemos en el curso.
4.7 Plano inclinado.
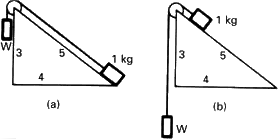
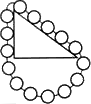
El principio de la conservación de la energía es muy útil para deducir lo que sucederá en diversas circunstancias. En la escuela secundaria aprendimos muchas leyes sobre poleas y palancas utilizadas de diferentes maneras. Podemos ahora ver que todas estas «leyes» son la misma, y que no había necesidad de memorizar 75 reglas para descubrirla. Un ejemplo simple lo constituye un plano inclinado liso que es, afortunadamente, un triángulo rectángulo de lados tres-cuatro-cinco (figura 4.7). Colguemos un peso de un kilogramo en el plano inclinado con una polea, y en el otro extremo de la polea colguemos un peso W. Queremos saber cuánto debe pesar W para equilibrar el peso de un kilogramo en el plano inclinado. ¿Cómo podemos descubrir la respuesta? Si decimos que está exactamente equilibrado, el sistema es reversible y por lo tanto puede subir y bajar, y podemos considerar la situación siguiente. En la situación inicial, (a), el peso de un kilogramo está en el extremo inferior del plano inclinado y el peso W está arriba. Una vez que W se ha deslizado hacia abajo de modo reversible, tenemos un peso de un kilogramo en la parte superior y el peso W ha descendido una distancia igual a la longitud del plano inclinado, (b), es decir, cinco metros, desde el nivel en el que estaba antes. Hemos elevado el peso de un kilogramo sólo tres metros y hemos hecho descender cinco metros el peso de W kilogramos. Por lo tanto, W = 3/5 de kilogramo. Nótese que dedujimos esto a partir de la conservación de la energía, y no a partir de componentes de fuerzas. La astucia, sin embargo, es relativa. Puede deducirse de un modo que es incluso más brillante, descubierto por Stevinus y grabado en su tumba. La figura 4.8 explica que tiene que ser 3/5 de kilogramo, porque la cadena no desliza y no da vueltas. Es evidente que la parte más baja de la cadena está equilibrada por sí misma, de modo que la tracción de los cinco pesos en un lado debe compensar la tracción de los tres pesos en el otro, o cualquiera que sea la proporción de los brazos. Mirando este diagrama ven ustedes que W debe ser 3/5 de kilogramo. (Si ustedes consiguen un epitafio como este en su tumba, están en el buen camino).
4.8 El epitafio de Stevinus.
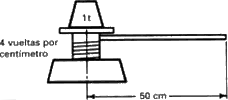
Ilustremos ahora el principio de la energía con un problema más complicado, el tornillo elevador mostrado en la figura 4.9 Para girar el tornillo, que tiene un paso de rosca de 4 vueltas por centímetro, se utiliza una manivela de medio metro de longitud. Nos gustaría saber cuánta fuerza habría que aplicar a la manivela para levantar una tonelada (1.000 kilogramos).
4.9 Un tornillo elevador.
Si queremos elevar la tonelada un centímetro, pongamos por caso, debemos dar cuatro vueltas completas a la manivela. Cuando ésta da una vuelta completa recorre aproximadamente 3,14 metros. Por lo tanto, la manivela debe recorrer un total de 12,5 metros, y si utilizásemos un sistema de poleas, etc., estaríamos levantando la misma tonelada con un peso menor W desconocido aplicado al extremo de la manivela. Así es como encontramos que W es aproximadamente 0,8 kilogramos. Esto es un resultado de la conservación de la energía.
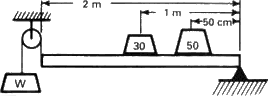
4.10 Barra con pesos apoyada en un extremo.
Tomemos ahora el ejemplo algo más complicado mostrado en la figura 4.10. Una varilla o barra de 2 metros de longitud está apoyada en un extremo. En mitad de la barra hay un peso de 30 kilogramos, y a una distancia de medio metro del apoyo hay un peso de 50 kilogramos. ¿Qué fuerza debemos aplicar hacia arriba en el extremo libre de la barra para mantenerla equilibrada, suponiendo que el peso de la propia barra es despreciable? Imaginemos que ponemos una polea en un extremo y colgamos un peso de la polea. ¿Cuál tendría que ser el peso W para mantener la barra equilibrada? Supongamos que el peso desciende una distancia arbitraria —para hacerlo fácil, supongamos que desciende 10 centímetros—, ¿a qué altura deberían subir los dos pesos de carga? El centro se eleva 5 centímetros, y el punto que está a un cuarto de la distancia desde el extremo fijo se eleva 2,5 centímetros. Por lo tanto, el principio de que la suma de las alturas multiplicadas por los pesos no cambia nos dice que el peso W multiplicado por 10 centímetros hacia abajo, más 30 kilogramos multiplicados por 5 centímetros hacia arriba, más 50 kilogramos multiplicados por 2,5 centímetros tiene que sumar cero:
−10W + (5)(30) + (2,5)(50) = 0; W = 27,5 Kg (4.11)
Así pues, debemos colgar un peso de 27,5 kilogramos para equilibrar la barra. De esta forma podemos calcular las leyes del «equilibrio»: la estática de puentes complicados, y demás. Este tratamiento se denomina principio de los trabajos virtuales, porque para aplicar este argumento tuvimos que imaginar que la estructura se mueve un poco; incluso si en realidad no se está moviendo o ni siquiera es móvil. Utilizamos el pequeñísimo movimiento imaginario para aplicar el principio de conservación de la energía.