¿Cuánto cable hará falta?

¿Cuánto cable hará falta?
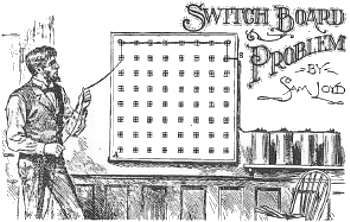
Para mostrar cuántas buenas ideas para acertijos pueden recogerse «de paso», les plantearé un problemita que se me pidió resolviera el otro día. Encontré a un electricista, que había inventado una especie de tablero, tratando de descubrir la manera más económica de pasar un fino cable de cobre por todos los puntos de contacto de su invento. El tablero era una cuestión elaborada, formada por varios cientos de puntos, pero 64 son suficientes para ilustrar nuestro problema.
El problema consiste en encontrar la más pequeña cantidad de cable que vaya desde el punto B hasta el centro del pequeño cuadrado marcado A. El cable debe pasar por los centros de los 64 cuadraditos. Cada cuadrado tiene una pulgada de lado y están espaciados de modo que sus centros estén a tres pulgadas de distancia entre sí. Cada vez que el cable describe un giro, es necesario enrollarlo alrededor de un ángulo del cuadrado, operación que demanda dos pulgadas de cable. No se permite realizar conexiones en diagonal.
Suponiendo que se necesiten dos pulgadas de cable para ir desde B hasta el centro del cuadrado más próximo, ¿puede usted determinar la menor longitud posible que hace falta para ir de B a A?