Es irónico que, en el mismo acertijo en que Loyd fustiga a «Alex el listo», quien piensa que todo lo sabe, el viejo maestro caiga en un grave error.

Tal como lo explica meticulosamente Henry Dudeney en Amusements in Mathematics, sólo los rectángulos con lados en ciertas proporciones pueden ser transformados en cuadrados por medio del método de la escalera. En este caso, los lados del rectángulo guardan la proporción de 3 a 4, lo que no permite la transformación deseada.

Dudeney presenta una limpia solución en cinco partes. No se ha descubierto nunca una solución en cuatro partes.

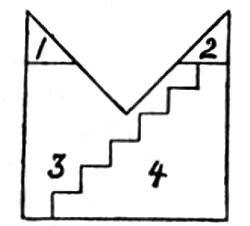
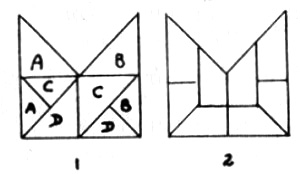
Incluso el viejo acertijo de la mitra de Loyd, que consiste en cortar la mitra en cuatro piezas de la misma forma y tamaño, sólo puede resolverse gracias a la poco satisfactoria suposición de que las piezas que llevan la misma letra, figura 1, están unidas por los ángulos y por lo tanto… ¡pueden considerarse una sola pieza! Loyd también publicó la más legítima disección en ocho piezas que muestra la fig. 2.

[M.G.]