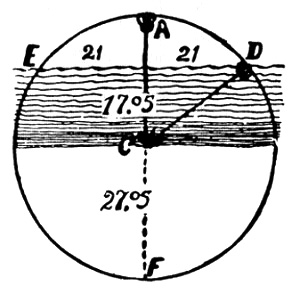
Dice Euclides: «Cuando dos cuerdas de arco se intersecan en el interior de un círculo, el producto de las partes de una será igual al producto de las partes de la otra». En la siguiente ilustración la superficie del agua forma la cuerda de un arco, y como cada parte de esta cuerda es de 21 pulgadas, el producto es 441 pulgadas.

El tallo del nenúfar forma la mitad de la otra cuerda, y como su altura por encima del agua forma una parte de la cuerda, esa parte, 10 pulgadas, multiplicada por la otra parte debe dar las mismas 441 pulgadas que se obtienen a partir del producto de las partes de la otra cuerda. De modo que dividimos 441 por 10, y obtenemos 44,1 pulgadas como medida de la otra parte de esa cuerda. Sumando 10 y 44,1, obtenemos la medida 54,1 como longitud de la cuerda desde A a F, que es el diámetro del círculo. Debemos dividirlo por la mitad para obtener el radio: 27,05. Como la flor se erguía a 10 pulgadas por encima de la superficie del agua, debemos deducir esas 10 pulgadas para obtener la profundidad del lago, que sería de 17,05 pulgadas.