
Figura 3.1. Mundo III de Karl Popper.
Los dos primeros capítulos se ocupaban del mundo físico y de las reglas matemáticas que utilizamos para describirlo, de lo notablemente precisas que son y lo extrañas que parecen a veces. En este tercer capítulo hablaré acerca del mundo mental y, en particular, sobre la relación que guarda con el mundo físico. Supongo que el obispo Berkeley habría pensado que, en cierto sentido, el mundo físico emerge de nuestro mundo mental, mientras que el punto de vista científico más general consiste en que la mentalidad es, de algún modo, una característica de algún tipo de estructura física.
Popper introdujo un tercer mundo llamado el mundo de la cultura (figura 3.1). Veía este mundo como un producto de la mentalidad y, por ello, utilizaba una jerarquía de mundos como se ilustra en la figura 3.2. En esta imagen, el mundo mental está relacionado en cierta manera —¿emerge de?— con el mundo físico y, de algún modo, la cultura surge de la mentalidad.

Figura 3.1. Mundo III de Karl Popper.

Figura 3.2.
Ahora quiero considerar las cosas de manera un poco diferente. Más que entender la cultura como algo que surge de nuestra mentalidad, como hizo Popper, prefiero creer que los mundos están conectados como se muestra en la figura 3.3. Más aún, mi «Mundo III» no es en realidad el mundo de la cultura sino el mundo platónico de las ideas —en particular la verdad matemática absoluta—. De esta forma, la disposición de la figura 1.3, que ilustra la dependencia profunda del mundo físico con respecto a leyes matemáticas exactas, está incorporada en nuestra ilustración.
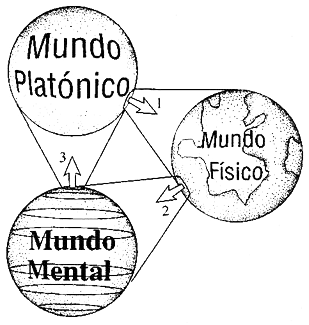
Figura 3.3. Tres Mundos y tres Misterios.
Gran parte de este capítulo estará dedicada a la relación que se establece entre todos estos mundos diferentes. Me parece que hay un problema fundamental con la idea de que la mentalidad surge de lo físico: es algo que preocupa a los filósofos por muy buenas razones. Los conceptos que tratamos en física son materia, objetos masivos, partículas, espacio, tiempo, energía, cosas físicas y demás. ¿Cómo puede ser que nuestras sensaciones, nuestra percepción de la rojez, o de la felicidad, tengan algo que ver con la física? Creo que esto es un misterio.
Podemos considerar las flechas que conectan los diferentes mundos en la figura 3.3 como misterios. En los dos primeros capítulos discutí la relación que existe entre las matemáticas y la física (Misterio 1), y cité el comentario de Wigner con respecto a esta relación. La consideraba muy extraordinaria y yo también lo hago. ¿A qué se debe que el mundo físico parezca obedecer leyes matemáticas de una forma extremadamente precisa? Y no solo eso, sino que las matemáticas que parecen tener el control de nuestro mundo físico son excepcionalmente fructíferas y potentes simplemente como matemáticas. Creo que esta relación es un profundo misterio.
En este capítulo examinaré el Misterio 2: el misterio de la relación entre el mundo físico y el mundo de la mentalidad. Pero, en relación con esto, tendremos también que considerar el Misterio 3: ¿qué subyace a nuestra capacidad de acceder a la verdad matemática? Cuando me referí al mundo platónico en los dos primeros capítulos, estaba hablando principalmente acerca de las matemáticas y de los conceptos matemáticos que uno tiene que invocar para describir el mundo físico. Uno tiene la sensación de que las matemáticas que son necesarias para describir estos problemas están ahí fuera.
Existe también, sin embargo, la sensación de que estas construcciones matemáticas son productos de nuestra mentalidad, es decir, que las matemáticas son un producto de la mente humana. Uno puede pensar las cosas de este modo, pero no es así realmente como el matemático considera la verdad matemática; y tampoco es esta mi forma de verla. Por ello, aunque hay una flecha que une el mundo mental y el mundo platónico, no pretendo indicar que esta, o de hecho cualquiera de estas flechas, significa que uno de estos mundos emerge simplemente de los otros. Aunque quizá en algún sentido están emergiendo, las flechas pretenden simplemente representar el hecho de que existe una relación entre los diferentes mundos.
Más importante es el hecho de que la figura 3.3 representa tres prejuicios propiamente míos. Uno de ellos es que el mundo físico entero puede, en principio, describirse en términos matemáticos. No estoy diciendo que todas las matemáticas puedan ser utilizadas para describir la física. Lo que afirmo es que, si uno escoge las partes correctas de las matemáticas, estas describen el mundo físico de forma muy precisa y, por ello, el mundo físico se comporta de acuerdo con las matemáticas. Así pues, existe una pequeña parte del mundo platónico que engloba nuestro mundo físico. Tampoco estoy diciendo que todos los elementos del mundo físico tengan su correspondencia en el mundo mental; más bien estoy sugiriendo que no existen objetos mentales flotando ahí fuera que no estén basados en la física. Este es mi segundo prejuicio. Existe un tercer prejuicio según el cual, en mi visión de las matemáticas, al menos en principio, cualquier objeto individual en el mundo platónico es accesible, en cierto sentido, a nuestra mentalidad. Algunas personas podrían preocuparse por este tercer prejuicio —de hecho, pueden sentirse inquietos por los tres prejuicios—. Tengo que decir que, solo después de haber dibujado este diagrama, me di cuenta de que reflejaba estos tres prejuicios personales míos. Volveré a él al final del capítulo.
Permítanme decir algo ahora sobre la consciencia humana. En particular, ¿es esta una cuestión sobre la que deberíamos pensar en términos de explicación científica? Mi punto de vista personal es decididamente que sí deberíamos hacerlo. En particular, tomo muy en serio la flecha que une el mundo físico con el mundo mental. En otras palabras, estamos ante el reto de comprender el mundo mental en términos del mundo físico.
He resumido algunas características del mundo físico y el mundo mental en la figura 3.4.
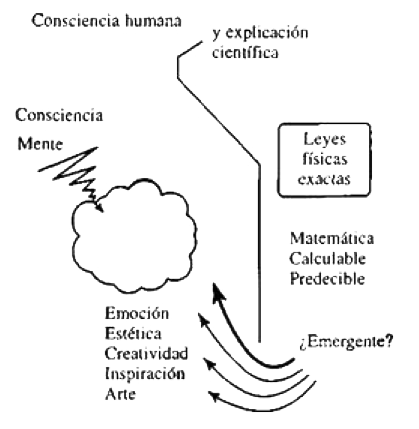
Figura 3.4.
En el lado derecho tenemos aspectos del mundo físico: este es percibido como si estuviera gobernado por leyes físicas y matemáticas precisas, como se discutió en los dos primeros capítulos. En el lado izquierdo situamos la consciencia, que pertenece al mundo mental, y palabras como alma, espíritu, religión y demás, aparecen con frecuencia. En la actualidad, se prefieren explicaciones científicas para las cosas. Más aún, se tiende a pensar que sería posible, en principio, introducir cualquier descripción científica en un ordenador. En consecuencia, si uno tiene un modelo matemático de algo, debería ser capaz, en principio, de programarlo en un ordenador. Esto es algo contra lo que argumentaré enérgicamente en este capítulo, a pesar de mi sesgo fisicalista.
Los términos utilizados para describir las leyes físicas en la figura 3.4 son predecible, calculable —estos tienen que ver con el hecho de si existe o no determinismo en nuestras leyes físicas y si podríamos o no utilizar un ordenador para simular la acción de estas leyes—. Por un lado, existe la opinión de que cualidades mentales como la emoción, la estética, la creatividad, la inspiración y el arte son ejemplos de cosas que serían difíciles de ver emergiendo de algún tipo de descripción computacional. En el extremo científico opuesto, algunas personas dirían: «nosotros somos simples ordenadores; quizá no sepamos cómo describir estas cosas aún, pero, de algún modo, si supiéramos el tipo correcto de cálculos que habría que realizar, seríamos capaces de describir todas las cualidades mentales enumeradas en la figura 3.4». A menudo se utiliza la palabra emergencia para describir este proceso. Estas cualidades emergen, según estas personas, como resultado del tipo correcto de actividad computacional.
¿Qué es la consciencia? No sé cómo definirla. Pienso que no es este el momento de intentar definir la consciencia, puesto que no sabemos qué es. Creo que es un concepto físicamente accesible; pese a todo, definirlo sería probablemente definir la cosa equivocada. Sin embargo, voy a describirla hasta cierto grado. Me parece que hay al menos dos aspectos diferentes en la consciencia. Por un lado, existen manifestaciones pasivas de la consciencia, que implican conocimiento. Utilizo esta categoría para incluir elementos como la percepción del color, de la armonía, el uso de la memoria, y así sucesivamente. Por otro lado, están sus manifestaciones activas, que implican conceptos como el libre albedrío y la realización de acciones voluntarias y conscientes. La utilización de tales términos refleja aspectos diferentes de nuestra consciencia.
Aquí me concentraré principalmente en aquello que implica la consciencia de un modo esencial. Es diferente de los aspectos pasivo y activo de la consciencia, y quizá está en algún lugar entre ambos. Me refiero al uso del término comprensión, o quizá intuición directa, que a menudo es una palabra más adecuada. No voy a definir ninguno de estos términos; no sé lo que significan. Existen otros dos términos que tampoco entiendo: conocimiento e inteligencia. Entonces, ¿por qué estoy hablando sobre cosas que no sé lo que significan realmente? Probablemente se debe a que soy un matemático y los matemáticos no pensamos tanto acerca de estos conceptos. No necesitamos definiciones precisas de los elementos que estamos manejando, con tal de que podamos decir algo sobre las relaciones entre ellos. El primer punto clave aquí es que opino que la inteligencia es algo que requiere comprensión. Utilizar el término inteligencia en un contexto en el que negamos que esté presente cualquier comprensión me parece poco razonable. De un modo análogo, comprender sin ningún conocimiento es también algo absurdo: comprender requiere algún tipo de conocimiento. Este es el segundo punto clave. De ello se deduce que la inteligencia requiere conocimiento. Aunque no estoy definiendo ninguno de estos términos, me parece razonable insistir sobre estas relaciones entre ellos.
Se podrían adoptar diversos puntos de vista acerca de la relación entre pensamiento consciente y computación. He resumido en la tabla 3.1 cuatro aproximaciones al conocimiento, que he designado A, B, C y D.
| A | Todo pensamiento es computación; en particular, las sensaciones de conocimiento consciente son producidas por la mera ejecución de cálculos apropiados. |
| B | La consciencia es una característica de la acción física del cerebro; y, mientras que cualquier acción física puede ser simulada computacionalmente, la simulación computacional no puede por sí misma producir consciencia. |
| C | La acción física apropiada del cerebro produce consciencia, pero esta acción física no puede siquiera ser propiamente simulada computacionalmente. |
| D | La consciencia no puede ser explicada en términos físicos, computacionales, o cualesquiera otros términos científicos. |
El punto de vista que llamo A, a veces denominado inteligencia artificial fuerte (IA fuerte) o funcionalismo (computacional), afirma que todo pensamiento es simplemente la realización de ciertos cálculos y, en consecuencia, si uno realiza los cálculos apropiados, el resultado será el conocimiento.
He designado como B al segundo punto de vista y, según este, en principio, sería posible simular la actividad de un cerebro cuando su propietario es conocedor de algo. La diferencia entre A y B es que, aunque dicha actividad puede ser simulada, esa mera simulación no podría en sí misma, según B, tener ningún sentimiento o ningún conocimiento —hay algo más, que quizá tiene que ver con la construcción física del objeto—. Por eso, un cerebro compuesto de neuronas y similares podría ser conocedor, mientras que una simulación de la actividad de dicho cerebro no sería conocedora. Este es, hasta donde puedo alcanzar, el punto de vista defendido por John Searle.
A continuación está mi propia manera de ver las cosas, que he llamado C. Estoy de acuerdo con B, hay algo en la actividad física del cerebro que provoca conocimiento —en otras palabras, hay algo en la física a lo que tenemos que dirigirnos—, pero esta actividad física es algo que ni siquiera puede ser simulado computacionalmente. No hay ninguna simulación que pudiera realizarse de dicha actividad. Esto requiere que exista algún factor en la actividad física del cerebro que esté más allá de la computación.
Finalmente, siempre existe el punto de vista D, según el cual es un error considerar estas cuestiones en términos de ciencia. Quizá el conocimiento no pueda ser explicado en términos científicos.
Yo soy un defensor del punto de vista C. Existen, sin embargo, diversas variedades de C. Está lo que podría denominarse C débil y C fuerte. C débil propone que, de algún modo, con la física conocida, bastaría solo con mirar con mucho cuidado para encontrar ciertos tipos de actividad que están más allá de la computación. Cuando digo «más allá de la computación», tengo que ser un poco más explícito, como lo seré en un instante. Según C débil, no hay nada que necesitemos buscar fuera de la física conocida para encontrar la actividad no computacional apropiada. C fuerte, por el contrario, requiere que exista algo fuera de la física conocida; nuestra comprensión física es inadecuada para la descripción del conocimiento. Es incompleta, y, como ustedes habrán deducido del capítulo 2, yo sí creo que nuestra imagen física es incompleta, como indiqué en la figura 2.17. Desde el punto de vista de la C fuerte quizá la ciencia futura explicará la naturaleza de la consciencia, pero la ciencia actual no lo hace.
Incluí algunas palabras en la figura 2.17 que no comenté en ese momento, en particular, el término computable. En la imagen estándar, uno se encuentra con física básicamente computable en el nivel cuántico, y el nivel clásico es, probablemente, computable, aunque hay cuestiones técnicas sobre cómo pasar desde sistemas discretos computables a sistemas continuos. Es un punto importante pero permítanme que no me ocupe aquí de ello. De hecho, me parece que los defensores de la C débil tendrán que encontrar algo en estas incertidumbres, algo que no pueda explicarse en términos de una descripción computable.
Para pasar del nivel cuántico al nivel clásico en la imagen convencional, introducimos el procedimiento que he llamado R, y que es una operación completamente probabilista. Lo que tenemos entonces es computabilidad junto con aleatoriedad. Voy a argumentar que esto no es suficiente: necesitamos algo diferente, y esta nueva teoría, que construye un puente entre estos dos niveles, tiene que ser una teoría no computable. Diré algo más sobre lo que entiendo por este término en un momento.
Esta es mi versión de la C fuerte: buscamos la no computabilidad en la física que forma un puente entre los niveles cuántico y clásico, lo cual es pedir bastante. Estoy diciendo que no solo necesitamos una nueva física, sino que también necesitamos una nueva física que sea relevante para la actividad del cerebro.
En primer lugar, abordemos la cuestión de si es plausible o no que exista algo más allá de la computación en nuestra comprensión. Permítanme exponerles un bonito ejemplo de un sencillo problema de ajedrez. En la actualidad, los ordenadores juegan muy bien al ajedrez. Sin embargo, cuando el problema de ajedrez que se muestra en la figura 3.5 fue planteado al ordenador más potente disponible en su época, el ordenador Pensamiento Profundo, este hizo una jugada muy estúpida.

Figura 3.5. Blancas juegan y hacen tablas: fácil para los seres humanos, pero ¡Pensamiento Profundo capturó la torre! (Problema planteado por William Hartston, tomado de un artículo de Jane Seymore y David Norwood en New Scientist, núm. 1889 pag. 23, 1993.
En esta posición de ajedrez, las piezas blancas están superadas en número por las negras: existen dos torres negras extra y un alfil negro. Esto debería constituir una enorme ventaja, si no fuera por el hecho de que una barrera de peones protege a todas las piezas negras. Así, todo lo que las blancas tienen que hacer es pasearse detrás de su barrera de peones blancos, y no hay posibilidad de perder la partida. Sin embargo, cuando se le presentó esta posición a Pensamiento Profundo, instantáneamente capturó la torre negra, abrió la barrera de peones y quedó en una posición irremediablemente perdida.
La razón de que hiciera eso es que había sido programado para calcular un cierto número de jugadas por anticipado y contar luego las piezas, o algo similar. En este ejemplo, ese no era el camino más adecuado. Por supuesto, si hubiera seguido calculando una jugada tras otra, y otra, algunas veces más, habría sido capaz de hacerlo. La cuestión es que el ajedrez es un juego computacional. En este caso, el jugador humano ve la barrera de peones y comprende que es impenetrable. El ordenador no tenía esa comprensión —simplemente computaba un movimiento tras otro—. Así pues, este ejemplo ilustra la diferencia que existe entre la mera computación y la cualidad de la comprensión.
He aquí otro ejemplo (figura 3.6). Es muy tentador capturar la torre negra con el alfil blanco, pero lo correcto es hacer como si el alfil blanco fuera un peón y utilizarlo para crear otra barrera de peones. Una vez que le hayamos enseñado a reconocer barreras de peones, el ordenador podrá ser capaz de resolver el primer problema pero fracasará en el segundo porque necesita un nivel de comprensión mayor.

Figura 3.6. Blancas juegan y hacen tablas: de nuevo fácil para los humanos, pero un ordenador normal que juege al ajedrez capturará la torre. (De un test de Turing por William Hartson y David Norwood).
Ustedes podrían pensar, no obstante, que con suficiente cuidado sería posible programar todos los niveles de comprensión posibles. Bien, quizá pueda hacerse con el ajedrez. El problema está en que el ajedrez es un juego computacional y, por eso, en última instancia, sería posible calcular todas las posibilidades hasta el final con un ordenador suficientemente potente. Esto supera la capacidad de los ordenadores actuales pero, en principio, sería posible. De todas formas, uno tiene la sensación de que en la comprensión hay algo más que la computación directa. Ciertamente, el modo en que enfocamos estos problemas de ajedrez es muy diferente de como lo hace un ordenador.
¿Podemos construir un argumento más fuerte a favor de que hay realmente algo en nuestra comprensión que es diferente de la computación? Sí podemos. No quiero consumir mucho tiempo en este argumento, aunque es la piedra básica de toda la discusión. Pero tengo que dedicarle un poco de tiempo, aunque el argumento pueda hacerse algo técnico. Las doscientas primeras páginas de Las sombras de la mente estaban dedicadas a tratar de mostrar que no hay cabos sueltos en el argumento que voy a ofrecerles.
Déjenme decir algo sobre computaciones. Las computaciones son lo que hace un ordenador. Los ordenadores reales tienen una capacidad de almacenamiento limitada pero voy a considerar un ordenador idealizado, una máquina de Turing, que difiere de un ordenador ordinario de propósito general solo en el hecho de que posee un espacio de almacenamiento ilimitado y puede seguir computando indefinidamente sin cometer errores y sin gastarse siquiera. Permítanme dar un ejemplo de computación. Una computación no tiene por qué involucrar simple aritmética sino que puede incluir también la realización de operaciones lógicas. Veamos un ejemplo:
Encontrar un número que no sea la suma de tres números cuadrados.
Por un número entiendo un número natural, tal como 0, 1, 2, 3, 4, 5, … y por números cuadrados, los números 02, 12, 22, 32, 42, 52, … He aquí cómo debería hacerlo usted: es una manera muy estúpida, pero ilustra lo que podemos entender por una computación. Empezamos con 0 y comprobamos si es la suma de tres números cuadrados. Buscamos todos los cuadrados que son menores o iguales que 0 y solo encontramos 02. Por consiguiente, solo podemos ensayar: 0 = 02 + 02 + 02; que resulta ser cierto y, por ello, 0 es la suma de tres cuadrados. A continuación ensayamos con 1. Escribimos todas las formas posibles de sumar todos los números cuyos cuadrados son menores que, o igual a uno y vemos si podemos sumar tres de ellos para obtener 1. Podemos hacerlo: 1 = 02 + 02 + 12. Podemos seguir de esta forma más bien tediosa, como se indica en la tabla 3.2, hasta que llegamos al número 7, donde podemos comprobar que no existe ninguna forma de sumar tres cuadrados de 02, 12 y 22 en cualquier combinación para que resulte el número 7 —todas las posibilidades se muestran en la tabla—. Así pues, 7 es la respuesta: es el número más pequeño que no es la suma de tres números cuadrados. Este ha sido un ejemplo de un cálculo.
| Ensayo 0 | cuadrados ≤ 0 | 02 | 0 = 02 + 02 + 02 |
| Ensayo 1 | cuadrados ≤ 1 | 02, 12 | 1 = 02 + 02 + 12 |
| Ensayo 2 | cuadrados ≤ 2 | 02, 12 | 2 = 02 + 12 + 12 |
| Ensayo 3 | cuadrados ≤ 3 | 02, 12 | 3 = 12 + 12 + 12 |
| Ensayo 4 | cuadrados ≤ 4 | 02, 12, 22 | 4 = 02 + 02 + 22 |
| Ensayo 5 | cuadrados ≤ 5 | 02, 12, 22 | 5 = 02 + 12 + 12 |
| Ensayo 6 | cuadrados ≤ 6 | 02, 12, 22 | 6 = 12 + 12 + 12 |
| Ensayo 7 | cuadrados ≤ 7 | 02, 12, 22 | 7 ≠ 02+ 02+ 02 7 ≠ 02+ 02+ 12 7 ≠ 02+ 02+ 22 7 ≠ 02+ 12+ 12 7 ≠ 02+ 12+ 22 7 ≠ 12+ 12+ 12 7 ≠ 12+ 12+ 22 7 ≠ 12+ 22+ 22 7 ≠ 22+ 22+ 22 |
En este ejemplo hemos tenido suerte porque el cálculo llegó a término, mientras que existen ciertos cálculos que no terminan nunca. Por ejemplo, supongamos que modifico ligeramente el problema:
Encontrar un número que no sea la suma de cuatro números cuadrados.
Existe un famoso teorema debido a Lagrange, un matemático del siglo XVIII, que demuestra que todo número puede expresarse como la suma de cuatro cuadrados. Por tanto, si procedemos de un modo mecánico para encontrar dicho número, el ordenador, simplemente, seguirá funcionando sin parar y nunca encontrará una respuesta. Esto ilustra el hecho de que existen algunas computaciones que no terminan.
La demostración del teorema de Lagrange es bastante complicada, así que he aquí otro teorema más fácil que, ¡espero todos puedan apreciar!
Encontrar un número impar que sea la suma de dos números pares.
Ustedes podrían programar su ordenador para llevarlo a cabo y el ordenador seguiría funcionando incesantemente porque sabemos que, cuando sumamos dos números pares, siempre obtenemos un número par.
Hay aquí un ejemplo esencialmente más complicado:
Encontrar un número par mayor que 2 que no sea la suma de dos números primos.
¿Termina alguna vez esta computación? La creencia general es que no lo hace, pero esto es una mera conjetura, conocida como la conjetura de Goldbach, y es tan difícil que nadie sabe con certeza si es verdadera o no. Así pues, hay (probablemente) tres cálculos que no se detienen: uno fácil, uno difícil y un tercero que es tan difícil que nadie sabe todavía si realmente se detiene o no.
Planteémonos ahora la siguiente pregunta:
¿Están utilizando los matemáticos algún algoritmo computacional (llamémosle A) para convencerse de que ciertas computaciones no terminan?
Por ejemplo, ¿tenía Lagrange algún tipo de programa de ordenador en su cabeza, que finalmente le llevó a la conclusión de que todo número es la suma de cuatro cuadrados? Ustedes no necesitan siquiera ser Lagrange: ustedes simplemente tienen que ser alguien que pueda seguir el argumento de Lagrange. Nótese que yo no estoy interesado en la cuestión de la originalidad, sino solamente en la cuestión de la comprensión. Por eso es por lo que he expresado la pregunta de la forma anterior: convencerse significa crear comprensión.
El término técnico para un enunciado de la naturaleza de los que estamos considerando es el de Π1-sentencia. Una Π1-sentencia es una afirmación de que cierta computación especificada no termina. Para apreciar el argumento que sigue, solo necesitamos pensar en sentencias de esta naturaleza. Quiero convencerles de que no existe tal algoritmo A. Para comprobar esto, necesito hacer una generalización. Tengo que hablar sobre computaciones que dependen de un número natural n.
Veamos algunos ejemplos:
Encontrar un número natural que no sea la suma de n números cuadrados.
Hemos visto por el teorema de Lagrange que si n es cuatro, o más, la computación no tiene fin. Pero si n es menor o igual que tres, entonces sí se para.
La siguiente computación es:
Encontrar un número impar que sea la suma de n números pares.
No importa cuál sea n —eso no va a ayudarle en absoluto—. El cálculo no se detiene para ningún valor de n.
Para la extensión de la conjetura de Goldbach, tenemos:
Encontrar un número par mayor que 2 que no sea la suma de tres o menos números primos.
Si la conjetura de Goldbach es verdadera, entonces esta computación no se detendrá para ningún n (distinto de 0 y 1). En cierto sentido, cuanto mayor es n, más fácil es esto. De hecho, creo que existe un valor suficientemente grande de n para el que se sabe que la computación es interminable.
El punto importante es que estos tipos de computación dependen del número natural n. Esto es, de hecho, fundamental para el famoso argumento conocido como argumento de Gödel. Lo discutiré en una forma debida a Alan Turing, pero utilizaré su argumento de un modo ligeramente diferente. Si a ustedes no les gustan los argumentos matemáticos, pueden desconectar por un momento: lo importante es el resultado. En cualquier caso, el argumento no es muy complicado, ¡tan solo algo confuso!
Los cálculos que actúan sobre un número n son básicamente programas de ordenador. Ustedes pueden hacer una lista de programas de ordenador y asignar un número, digamos p, a cada uno de ellos. De este modo ustedes introducen en su ordenador de propósito general algún número p y el ordenador empieza a funcionar, realizando dicha computación p-ésima aplicada a cualquier número n que ustedes hayan seleccionado. El número p se escribe como subíndice en nuestra notación. Así pues, hago una lista de dichos programas de ordenador, o computaciones, que actúan sobre el número n, colocándolos uno detrás de otro.
C0(n), C1(n), C2(n), C3(n), …, Cp(n), …
Vamos a suponer que ésta es una lista de todas las posibles computaciones C(n) y que podemos encontrar algún modo efectivo de ordenar estos programas de ordenador, de modo que el número p designe al p-ésimo programa en la ordenación. Entonces, Cp(n) representa el p-ésimo programa aplicado al número natural n.
Supongamos ahora que disponemos de algún procedimiento computacional, o algorítmico (A) que puede actuar sobre un par de números (p, n), y tal que, cuando dicho procedimiento llega a un final, nos proporciona una demostración válida de que la computación C(n) no termina. El algoritmo A no siempre funcionará necesariamente, en el sentido de que puede haber algunas computaciones C(n) que sean interminables cuando A(p,n) tampoco termina. Pero quiero insistir en que A no comete errores y, por eso, si A(p,n) sí termina, Cp(n) no lo hace. Tratemos de imaginar que los matemáticos humanos actúan de acuerdo con algún procedimiento computacional A cuando formulan (o siguen) cierta demostración matemática rigurosa de una proposición matemática (digamos, de una Π1-sentencia). Supongamos que también se les permite conocer qué es A y que ellos creen que es un procedimiento válido. Vamos a tratar de imaginar que A engloba todos los procedimientos a disposición de los matemáticos humanos para demostrar convincentemente qué computaciones no se detienen. El procedimiento A empieza considerando la letra p para seleccionar el programa de ordenador, y luego considera el número n para descubrir sobre qué número debe actuar. Entonces, si el procedimiento computacional A llega a término, ello implica que la computación C(n) no termina. Así pues:
si A(p,n) se para, entonces C(n) no se para. (1)
En esto consiste el trabajo de A: proporciona la forma de convencerse incuestionablemente de que ciertas computaciones no terminan.
Supongamos ahora que ponemos p = n. Esto puede parecer algo curioso. Es el famoso procedimiento conocido como procedimiento diagonal de Cantor y no hay nada erróneo en usarlo. Entonces llegamos a la conclusión de que:
si A(n,n) se para, entonces Cn(n) no se para.
Pero ahora, A(n,n) depende solo de un número y, por ello, A(n,n) debe ser uno de los programas de ordenador C(n), puesto que la lista es exhaustiva para computaciones que actúan sobre una única variable n. Supongamos que el programa de ordenador que es idéntico a A(n,n) viene designado por k. Entonces,
A(n,n) = Ck(n).
Ahora hacemos n = k y encontramos que:
A(k,k) = Ck(k).
Entonces, consideramos el enunciado (1) y concluimos que: si A(k,k) se para, entonces Ck(k) no se para.
Pero A(k,k) es lo mismo que Ck(k). Por consiguiente, si Ck(k) se para, entonces no se para. Eso significa que no se para: es pura lógica. Pero aquí está la trampa: esta computación particular no se para y, si creemos en A, entonces también debemos creer que Ck(k) no se para. Pero A tampoco se para y, por tanto, no sabe que Ck(k) no se para. Por consiguiente, el procedimiento computacional no puede, después de todo, englobar la totalidad del razonamiento matemático para decidir que ciertas computaciones no se paran —es decir, para establecer la verdad de Π1-sentencia—. Esto es lo esencial del argumento de Gödel-Turing en la forma en que lo necesito.
Ustedes pueden cuestionarse la fuerza global de este argumento. Lo que afirma claramente es que la intuición matemática no puede ser codificada en forma de alguna computación de la que podamos saber que es correcta. Las personas discuten a veces sobre esto pero a mí me parece que es una implicación clara. Es interesante leer lo que Turing y Gödel decían acerca de este resultado. He aquí la afirmación de Turing:
«En otras palabras, si se espera que una máquina sea infalible, no puede ser también inteligente. Existen varios teoremas que dicen casi exactamente eso. Pero estos teoremas no dicen casi nada sobre cuánta inteligencia puede ser mostrada si una máquina no tiene pretensiones de infalibilidad».
Por eso, su idea era que los argumentos tipo Gödel-Turing pueden ser reconciliados con la idea de que los matemáticos son esencialmente ordenadores si los procedimientos algorítmicos de acuerdo con los que actúan, para discernir la verdad matemática, son básicamente inválidos. Podemos restringir la atención a enunciados aritméticos, por ejemplo, (Π1-sentencias, que constituyen un tipo muy restrictivo de enunciados). Creo que Turing pensaba que la mente humana utiliza algoritmos, pero que dichos algoritmos son simplemente erróneos —esto es, son realmente inválidos—. Yo encuentro que esta es una posición bastante poco plausible, especialmente porque uno no está interesado aquí en cómo podría obtener inspiración, sino simplemente en cómo podría seguir un argumento y comprenderlo. Me parece que la postura de Turing no es muy encomiable. Según mi esquema, Turing habría sido una persona del tipo A.
Veamos lo que pensaba Gödel. En mi esquema, él era una persona del tipo D. Así, incluso si Turing y Gödel tenían la misma evidencia ante sí, ambos llegaban a conclusiones esencialmente opuestas. De todas formas, aunque Gödel no creía que la intuición matemática pudiera reducirse a computación, no fue capaz de descartar rigurosamente esta posibilidad. He aquí lo que decía:
«Por otra parte, sobre la base de lo que se ha demostrado hasta ahora, sigue siendo posible que pueda existir (e incluso sea empíricamente descubierta) una máquina capaz de demostrar teoremas que, de hecho, sea equivalente a la intuición matemática, pero que no puede probarse que sea así, ni puede probarse que produzca solo teoremas correctos de la teoría de números finitos».
Su argumento era que existe una escapatoria para el uso directo del argumento de Gödel-Turing como refutación del computacionalismo (o funcionalismo), a saber: que los matemáticos podrían estar utilizando un procedimiento algorítmico que es válido pero del que no podemos saber con seguridad que es válido. Así pues, era la parte cognoscible la que Gödel pensaba que constituía una escapatoria, y era la parte válida aquella por la que se decidió Turing.
Mi opinión es que ninguna de estas es un posible desarrollo del argumento. Lo que dice el teorema de Gödel-Turing es que si se encuentra que un procedimiento algorítmico (para establecer Π1-sentencias) es válido, entonces uno puede mostrar inmediatamente algo que se sale de ello. Pudiera ser que estemos utilizando un procedimiento algorítmico del que no puede saberse que es válido y podría haber algún tipo de dispositivo de aprendizaje que nos permita desarrollar esta capacidad. Estos temas, y muchos otros, son tratados ad nauseam en mi libro Las sombras de la mente. No quiero entrar aquí en estas digresiones, solo mencionaré dos puntos.
¿Cómo podría haber aparecido este supuesto algoritmo? En el caso de los seres humanos, presumiblemente tendría que haber sido resultado de la selección natural, o, en el caso de los robots, habría sido construido por IA (Inteligencia Artificial) deliberada. No entraré en detalle en estos argumentos sino que simplemente los ilustraré con dos dibujos de mi libro.
El primer dibujo tiene que ver con la selección natural (figura 3.7).

Figura 3.7. Para nuestros ancestros remotos, una capacidad específica para hacer matemáticas sofisticadas difícilmente puede haber sido una ventaja selectiva, pero sí pudo haberlo sido perfectamente una capacidad para comprender.
Ustedes pueden ver que el matemático no está en una posición muy cómoda desde el punto de vista de la selección natural porque hay un tigre de dientes afilados dispuesto a saltar sobre él. Por el contrario, sus primos, en la otra parte del dibujo, están cazando mamuts, construyendo casas, recogiendo cosechas y otras labores. Estas actividades implican comprensión pero no son específicas de las matemáticas. Así pues, es posible que la cualidad de la comprensión fuera la causa por la que fuimos seleccionados, pero no es posible que lo fueran los algoritmos específicos para hacer matemáticas.
El otro dibujo tiene que ver con la construcción IA deliberada y hay una pequeña historia en mi libro acerca de un experto en IA del futuro que mantiene una discusión con el robot (figura 3.8).
Figura 3.8. Ignacio Almirante se enfrenta al Joven Cibersistema Matemático. Las primeras 200 páginas de Las sombras de la mente están dedicadas a responder a las críticas respecto a la utilización del argumento de Gödel-Turing. La esencia de estos nuevos argumentos está contenida en el diálogo entre la persona I.A. y su robot.
El argumento completo dado en el libro es algo largo y complicado —no creo que sea necesario entrar aquí en ello—. Mi uso original del argumento de Gödel-Turing había sido atacado por todo tipo de personas desde todo tipo de ángulos diferentes y era necesario responder a todos esos ataques. Traté de resumir la mayoría de estos nuevos argumentos presentados en Las sombras de la mente, en la discusión que la persona IA mantiene con su robot.
Permítanme volver a la cuestión de lo que está pasando. El argumento de Gödel se refiere a enunciados particulares sobre números. Lo que Gödel nos dice es que ningún sistema de reglas computacionales puede caracterizar las propiedades de los números naturales. Pese al hecho de que no hay forma computacional de caracterizar los números naturales, cualquier niño sabe lo que son. Todo lo que hacemos es mostrar al niño números diferentes de objetos, como se ilustra en la figura 3.9, y, al cabo de cierto tiempo, puede abstraer la noción de número natural a partir de estos ejemplos concretos.
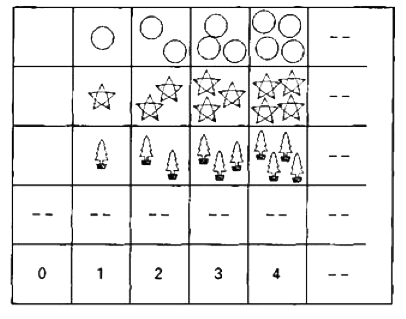
Figura 3.9. La noción platónica de un número natural puede ser abstraída por un niño a partir de tan sólo unos pocos ejemplos simples.
No damos al niño un conjunto de reglas computacionales, lo que estamos haciendo es capacitar al niño para comprender qué son los números naturales. Yo diría que el niño es capaz de establecer algún tipo de contacto con el mundo platónico de las matemáticas. Algunas personas no son partidarias de esta manera de hablar sobre la intuición matemática pero, de todas formas, me parece que uno tiene que adoptar alguna posición de esta naturaleza acerca de lo que está sucediendo. De algún modo, los números naturales están ya ahí, existiendo en algún lugar del mundo platónico, y tenemos acceso a dicho mundo a través de nuestra capacidad para ser conocedores de cosas. Si fuéramos simplemente ordenadores electrónicos, no tendríamos dicha capacidad. Las reglas no son los factores que nos capacitan para comprender la naturaleza de los números naturales, como muestra el teorema de Gödel. Comprender qué son los números naturales es un buen ejemplo del contacto con el mundo platónico.
Así pues, lo que estoy diciendo, con más generalidad, es que la comprensión matemática no es algo computacional, sino algo bastante diferente que depende de nuestra capacidad de ser conocedores de cosas. Algunas personas podrían decir: «Bien, todo lo que usted afirma haber demostrado es que la intuición matemática no es computacional. Eso no dice mucho sobre otras formas de consciencia». Pero me parece que esto ya es bastante. Es poco razonable trazar una línea entre la comprensión matemática y cualquier otro tipo de comprensión. Eso es lo que yo estaba tratando de ilustrar con mi primer dibujo (figura 3.7). La comprensión no es específica de las matemáticas. Los seres humanos desarrollan esta habilidad de comprensión general y no es una habilidad computacional porque la comprensión matemática no lo es. Tampoco trazo una línea divisoria entre la comprensión matemática y la consciencia humana en general. Por eso, aunque dije que no sé qué es la consciencia humana, me parece que la comprensión humana es un ejemplo de ella, o, al menos, es algo que la requiere. Tampoco voy a trazar una línea entre la consciencia humana y la consciencia animal. Aquí podría tener dificultades con diferentes conjuntos de personas. Me parece que los seres humanos son muy similares a muchos otros tipos de animales y, aunque podemos tener una comprensión de las cosas algo mejor que algunos de nuestros primos, en cualquier caso ellos también poseen algún tipo de comprensión, y por eso deben tener también conocimiento.
Por consiguiente, la no-computabilidad en algún aspecto de la consciencia y, específicamente, en la comprensión matemática, sugiere fuertemente que la no-computabilidad debería ser una característica de toda la consciencia. Esta es mi hipótesis.
Ahora bien, ¿qué entiendo por no-computabilidad? He hablado mucho sobre ello pero debería dar un ejemplo de algo que sea no-computacional para mostrar qué quiero decir. Lo que voy a describirles es un ejemplo de lo que a menudo se denomina un modelo de Universo de juguete —es el tipo de actividades que ocupan a los físicos cuando no pueden pensar en nada mejor que hacer— y, ¡no es una actividad tan fútil! Lo propio de un modelo de juguete es que no pretende ser un modelo real del Universo, puede reflejar algunas de sus características pero no pretende ser tomado en serio como un modelo del Universo real. Este modelo de juguete concreto no pretende, ciertamente, ser tomado en serio en este sentido. Se presenta solo para ilustrar un determinado aspecto.
En este modelo, existe un tiempo discreto que corre 0, 1, 2, 3, 4, … y el estado del Universo en cualquier instante viene dado por un conjunto poliomino. ¿Qué es un conjunto poliomino? Algunos ejemplos se ilustran en la figura 3.10.
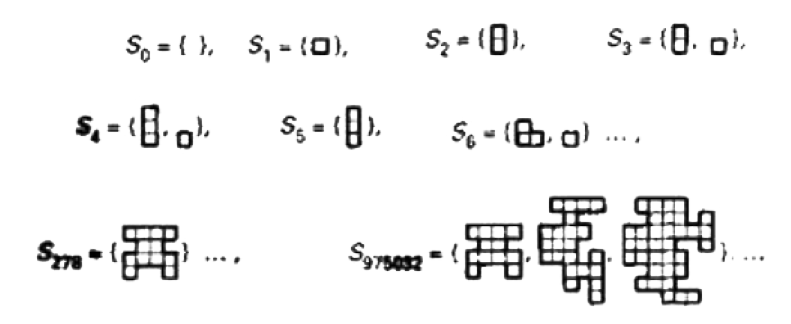
Figura 3.10. Un modelo de juguete no computable para el Universo. Los diferentes estados de este Universo de juguete determinista pero no computable están dados en términos de pares de conjuntos finitos de poliominos. Si el primer conjunto del par tesela el plano, la evolución temporal procede con un aumento del orden numérico del primer conjunto, mientras que el segundo marca el tiempo. Cuando el primer conjunto no tesela el plano, los dos se permutan antes de que la evolución continúe. Seria algo así como: (S0, S0), (S0, S1), (S1, S1), (S2, S1), (S3, S1), (S4, S1), …, (S278, S251), (S251, S278), (S252, S279), …
Un poliomino es una colección de cuadrados, todos ellos pegados a lo largo de aristas diversas para dar lugar a alguna forma plana. Estoy interesado en conjuntos de poliominos. Ahora, en este modelo de juguete, el estado del Universo en un instante viene dado por dos conjuntos finitos independientes de poliominos. En la figura 3.10 expongo una lista completa de todos los posibles conjuntos finitos de poliominos, enumerados S0, S1, S2, … de alguna forma computacional. ¿Cuál es la evolución, o la dinámica, de este ridículo Universo? Empezamos en el instante cero, con los conjuntos de poliominos (S0, S0), y luego continuamos con otro par de conjuntos de poliominos de acuerdo con cierta regla precisa. Esta regla depende de si es posible o no utilizar un conjunto de poliominos dado para teselar el plano entero utilizando solamente los poliominos de dicho conjunto.
La pregunta entonces es: ¿es posible cubrir el plano entero sin dejar huecos o sin que haya solapamientos utilizando solo los poliominos del conjunto dado? Supongamos ahora que el estado del Universo del modelo de juguete en cierto instante es el par de conjuntos de poliominos (Sq, Sr). La regla para la evolución de este modelo consiste en que, si es posible teselar el plano con los poliominos de Sq, entonces pasamos al siguiente Sq+1, lo que da el par (Sq+1, Sr) en el próximo instante de tiempo. Si no es posible hacerlo, entonces debemos además permutar el par para obtener (Sr, Sq+1). Es un Universo pequeño muy simple y estúpido —¿qué pasa con él?—. Lo que sucede es que, aunque su evolución es enteramente determinista —les he proporcionado una regla determinista absoluta y muy clara acerca de cómo va a evolucionar el Universo— es no-computable. Se sigue de un teorema de Robert Berger que no hay ninguna operación de ordenador que pueda simular la evolución de este Universo porque no hay procedimiento decisorio computacional para decidir cuándo un conjunto de poliominos teselará el plano.
Esto ilustra el hecho de que computabilidad y determinismo son conceptos diferentes. Algunos ejemplos de teselados por poliominos se muestran en la figura 3.11.
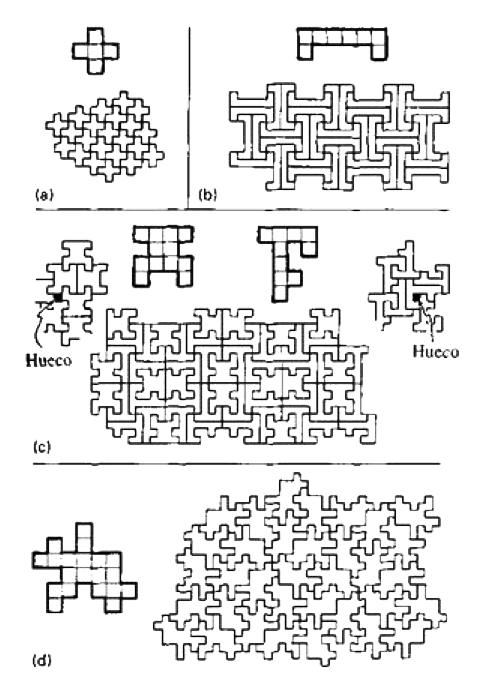
Figura 3.11. Diversos conjuntos de poliominos que teselarán el plano euclidiano infinito (si se permiten las teselas reflejadas). Sin embargo, ninguno de los poliominos del conjunto (c), por sí solo, teselará el plano.
En los ejemplos (a) y (b), estas formas pueden teselar un plano completo, tal como se ilustra. En el ejemplo (c), las formas de la izquierda o de la derecha por sí solas no pueden teselar un plano —en ambos casos dejan huecos—. Pero, tomadas juntas, pueden teselar el plano entero, como se ilustra en (c). El ejemplo (d) teselará también el plano —solo puede teselar el plano en la forma mostrada y esto ilustra lo complejos que pueden llegar a ser estos teselados.
No obstante, las cosas pueden empeorar. Permítanme mostrarles el ejemplo de la figura 3.12; de hecho, el teorema de Robert Berger depende de la existencia de conjuntos de teselas como este.
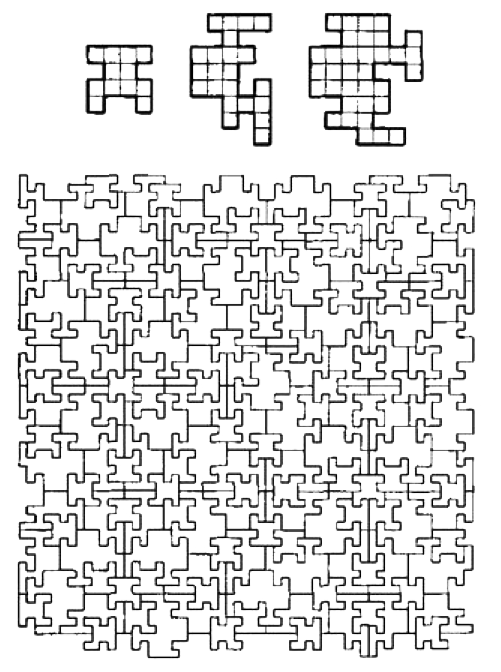
Figura 3.12. este conjunto de tres poliominos teselará el plano sólo de forma aperiódica.
Las tres teselas mostradas en la parte superior de la figura cubrirán el plano entero, pero no hay forma de hacer esto de tal modo que la figura se repita. Es siempre diferente a medida que sigamos avanzando y no es fácil ver lo que podemos hacer realmente con ello. Pero, en cualquier caso, puede hacerse y la existencia de teselados como estos entran en el argumento de Robert Berger a partir del cual se sigue que no hay programa de ordenador que pueda simular este universo de juguete.
¿Qué pasa con el Universo real? En el capítulo 2 he argumentado que en nuestra física está ausente algo fundamental. ¿Existe alguna razón derivada de la propia física para pensar que pudiera haber algo no-computable en dicha física ausente? Creo que hay algunas razones para creer esto: que la verdadera teoría de la gravitación cuántica podría ser no-computable. La idea no es en absoluto descabellada. Señalaré que la no-computabilidad es una característica de dos aproximaciones independientes a la gravedad cuántica. Lo que es característico de estas aproximaciones concretas es que involucran la superposición cuántica de espacio-tiempos tetradimensionales. Muchas otras aproximaciones involucran solo superposiciones de espacios tridimensionales.
La primera es el esquema de Geroch-Hartle para la gravedad cuántica, que resulta tener un elemento no-computable, ya que invoca un resultado, debido a Markov, que afirma que las cuatro variedades topológicas no son computacionalmente clasificables. No entraré en esta cuestión técnica, pero ello demuestra que esta característica de la no-computabilidad ha surgido ya de forma natural en los intentos de combinar la teoría general de la relatividad y la mecánica cuántica.
El segundo lugar donde ha surgido la no-computabilidad en una aproximación a la gravedad cuántica es en la obra de David Deutsch. Apareció en un borrador previo que distribuyó, pero luego, para mi pesar, cuando el artículo apareció en prensa, ¡el argumento no se encontraba por ninguna parte! Le pregunté acerca de ello y me aseguró que lo suprimió, no porque estuviese equivocado, sino porque no era relevante para el resto del artículo. Su punto de vista es que, en estas divertidas superposiciones de espacio-tiempos, uno tiene que considerar al menos la posibilidad de que algunos de estos Universos potenciales pudieran tener líneas cerradas de tipo tiempo (figura 3.13).
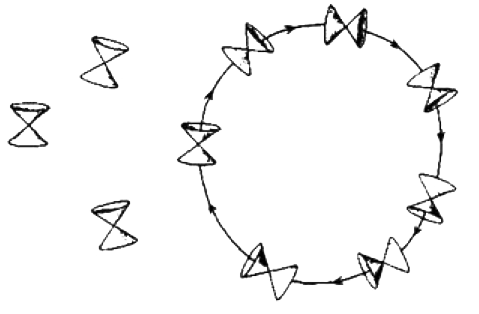
Figura 3.13. Con una inclinación suficientemente grande de los conos de luz, en el espacio-tiempo pueden darse líneas cerradas de tipo tiempo.
En ellos, la causalidad se ha vuelto loca, futuro y pasado se mezclan, y las influencias causales se cierran en círculos. Ahora bien, aunque estas líneas cerradas solo tienen que jugar un papel como hechos contrafácticos, como en el problema de comprobación de bombas del capítulo 2, siguen ejerciendo influencia en lo que sucede realmente. Yo no diría que este es un argumento claro, pero es, al menos, un indicio de que fácilmente podría haber algo de naturaleza no-computacional en la teoría correcta, si es que la encontramos alguna vez.
Quiero plantear otra cuestión. Resalté que el determinismo y la computabilidad son conceptos diferentes. Ello tiene que ver ligeramente con la cuestión del libre albedrío.
En discusiones filosóficas, el libre albedrío ha sido siempre considerado en términos de determinismo. En otras palabras: «¿está nuestro futuro determinado por nuestro pasado?», y otras cuestiones de esta naturaleza. Me parece que podrían plantearse otras muchas preguntas; por ejemplo: «¿está el futuro determinado computablemente por el pasado?» —esta es una cuestión diferente—.
Estas consideraciones plantean todo tipo de cuestiones diversas. Yo solo las plantearé —ciertamente no trataré de responderlas—. Siempre hay grandes discusiones acerca de hasta qué punto nuestras acciones están determinadas por nuestra herencia y nuestro ambiente. Y es extraño que no se mencione demasiado a menudo el papel de los elementos aleatorios. En cierto sentido, todas estas cosas están más allá de nuestro control. Ustedes podrían plantear la siguiente pregunta: «¿hay algo más, quizá una cosa denominada el yo, que es diferente de todas estas y que reside más allá de tales influencias?». Incluso asuntos legales tienen relevancia en el marco de una idea semejante. Por ejemplo, las cuestiones de derechos o responsabilidades parecen depender de las acciones de un yo independiente. Pero esto puede ser algo muy sutil. En primer lugar, existe la cuestión relativamente directa del determinismo y no-determinismo. El tipo normal de no-determinismo implica precisamente elementos aleatorios, pero eso no nos ayuda mucho. Estos elementos aleatorios siguen estando más allá de nuestro control. Podríamos tener en su lugar no-computabilidad, podríamos tener tipos de no-computabilidad de orden superior. En realidad es curioso que los argumentos del tipo de los de Gödel que he presentado pueden aplicarse de hecho en diferentes niveles. Pueden hacerlo en el nivel de lo que Turing llama máquinas oráculo: el argumento es realmente mucho más general que el que presenté más arriba. Por eso, uno tiene que considerar la cuestión de si podría o no existir algún tipo no-computabilidad de orden superior involucrado en la forma en que evoluciona Universo real. Quizá nuestras sensaciones de libre albedrío tengan algo que ver con esto.
He hablado del contacto con algún tipo de mundo platónico: ¿cuál es la naturaleza de este contacto platónico? Existen algunos tipos de palabras que parecerían involucrar elementos no-computables: juicio, sentido común, intuición, sensibilidad estética, compasión, moralidad… Creo que estas cualidades no son simples características de la computación. Hasta ahora, he hablado del mundo platónico principalmente en términos de matemáticas, pero hay otros elementos que uno también podría incluir. Platón argumentaría ciertamente que no sólo lo verdadero, sino también lo bueno y lo bello, son conceptos (platónicos) absolutos. Si existe algún tipo de contacto con los absolutos platónicos que nuestro conocimiento nos permite lograr, y que no puede explicarse en términos de comportamiento computacional, entonces creo que ésa es una cuestión importante.
¿Qué sucede con nuestros cerebros? La figura 3.14 muestra algo de un cerebro.
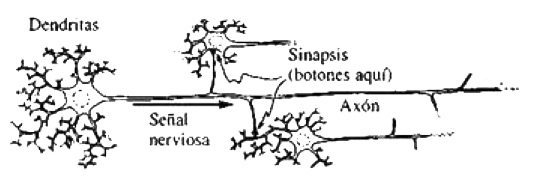
Figura 3.14. Un esbozo de una neurona, conectada a otras por medio de sinapsis.
Un constituyente principal del cerebro es su sistema de neuronas. Una parte importante de cada neurona es una fibra muy larga conocida como su axón. El axón se bifurca en ramas separadas en diversos lugares y cada una de estas ramas termina finalmente en una sinapsis. Estas sinapsis son las uniones donde las señales se transfieren desde cada neurona a (principalmente) otras neuronas por medio de sustancias químicas llamadas neurotransmisores. Algunas sinapsis son de naturaleza excitadora, con neurotransmisores que tienden a reforzar la activación de la neurona siguiente, y otras son inhibidoras, con tendencia a suprimir la activación de la siguiente neurona.
Podemos referirnos a la fiabilidad de una sinapsis al pasar mensajes de una neurona a la siguiente como la intensidad de la sinapsis. Si todas las sinapsis tuvieran intensidades fijas, el cerebro sería muy parecido a un ordenador, pero se da el caso de que estas intensidades sinápticas pueden cambiar y existen diversas teorías acerca de cómo cambian. Por ejemplo, el mecanismo de Hebb fue una de las primeras sugerencias para este proceso. La cuestión es, sin embargo, que todos los mecanismos que se han sugerido para inducir cambios son de naturaleza computacional, aunque con elementos probabilistas adicionales. Por eso, si tenemos algún tipo de regla probabilista-computacional que nos diga cómo cambian estas intensidades, entonces aún podremos simular la acción del sistema de neuronas y sinapsis mediante un ordenador (puesto que los elementos probabilistas también pueden ser fácilmente simulados computacionalmente) y obtener el tipo de sistema ilustrado en la figura 3.15.
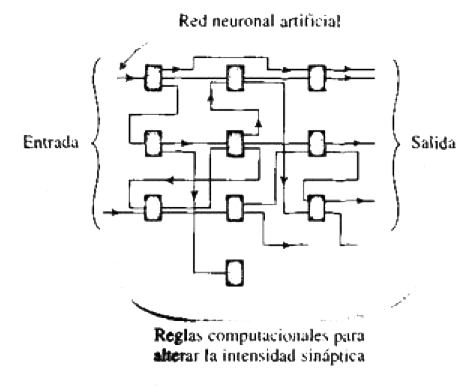
Figura 3.15.
Las unidades ilustradas en la figura 3.15, que podemos imaginar que son transistores, podrían desempeñar el papel de las neuronas en el cerebro. Por ejemplo, podemos considerar dispositivos electrónicos específicos conocidos como redes neuronales artificiales. En estas redes están incorporadas varias reglas concernientes a cómo cambian las intensidades de las sinapsis, normalmente para mejorar la calidad de alguna señal de salida. Pero las reglas son siempre de naturaleza computacional. Es fácil ver que esto debe ser así, por la muy buena razón de que estas cosas se simulan en ordenadores. Esa es la prueba: si uno es capaz de introducir el modelo en un ordenador, entonces es computable. Por ejemplo, Gerald Edelman tiene algunas sugerencias sobre cómo podría trabajar el cerebro que, según él, no son computacionales. ¿Cómo lo consigue? Edelman tiene un ordenador que simula todas estas sugerencias. Por eso, si hay un ordenador que se supone que lo simula, entonces es computacional.
Quiero abordar la cuestión siguiente: «¿qué están haciendo las neuronas individuales? ¿Están actuando simplemente como unidades computacionales?». Las neuronas son células y las células son estructuras muy elaboradas. De hecho, son tan elaboradas que, incluso si tuviéramos solo una de ellas, todavía podríamos seguir haciendo cosas muy complicadas. Por ejemplo, un paramecio, un ser unicelular, puede nadar hacia el alimento, alejarse del peligro, sortear obstáculos y, aparentemente, aprender por experiencia (figura 3.16).

Figura 3.16. Un paramecio. Nótense los cilios similares a pelos que son utilizados para nadar. Estos cilios forman las extremidades externas del citoesqueleto del paramecio.
Todas estas son cualidades que uno pensaría que requieren un sistema nervioso pero, ciertamente, el paramecio no tiene sistema nervioso. Lo mejor que podría pasar es que, ¡el paramecio fuera una neurona en sí mismo! Evidentemente no hay neuronas en un paramecio: hay solo una única célula. Una afirmación semejante podría hacerse para una ameba. La pregunta es, ¿cómo lo hace?
Una sugerencia es que el citoesqueleto —la estructura que, entre otras cosas, confiere su forma al paramecio— es lo que está controlando las acciones complejas de estos animales unicelulares. En un paramecio, los pequeños pelos, o cilios, que utiliza para nadar son los extremos del citoesqueleto, y están constituidos básicamente por pequeñas estructuras tubulares llamadas microtúbulos. El citoesqueleto está hecho de estos microtúbulos, además de actina y filamentos intermedios. Las amebas también se mueven, utilizando microtúbulos para impulsar sus pseudópodos.
Los microtúbulos son cosas extraordinarias. Los cilios, que los paramecios utilizan para nadar, son básicamente haces de microtúbulos. Además, los microtúbulos están fuertemente involucrados en la mitosis, es decir, en la división celular. Esto es cierto para los microtúbulos de las células ordinarias pero no, aparentemente, para las neuronas: las neuronas no se dividen y esto puede ser una diferencia importante. El centro de control del citoesqueleto es una estructura conocida como el centrosoma, cuya parte más prominente, el centriolo, consiste en dos haces de microtúbulos que forman una «T» separada. En una fase crítica, cuando el centrosoma se divide, cada uno de los dos cilindros del centriolo genera otro, de modo que se forman dos centriolos que luego se separan, y cada uno de ellos parece arrastrar un haz de microtúbulos con él. Estas fibras de microtúbulos conectan de algún modo las dos partes del centrosoma dividido con las hebras de ADN separadas en el núcleo de la célula y, entonces, dichas hebras de ADN se separan. Este proceso inicia la división celular.
Esto no es lo que sucede en las neuronas, porque las neuronas no se dividen, de modo que los microtúbulos deben de estar haciendo alguna otra cosa. ¿Qué están haciendo en las neuronas? Bien, probablemente montones de cosas, incluyendo el transporte de moléculas neurotransmisoras dentro de la célula, pero una actividad en la que sí parecen estar involucrados es en la determinación de las intensidades de las sinapsis. En la figura 3.17 se muestra una ampliación de una neurona y una sinapsis, donde también se indican las posiciones aproximadas de los microtúbulos, así como de las fibras de actina. Una forma posible de que los microtúbulos afectaran a la intensidad de la sinapsis es que tuvieran influencia en la naturaleza de una espina dendrítica (figura 3.17).
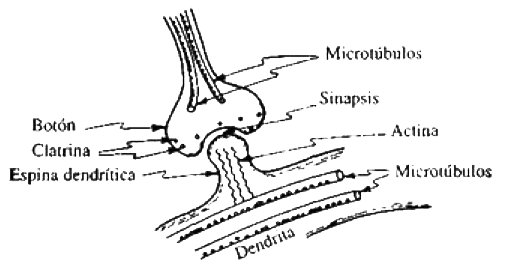
Figura 3.17. Las clatrinas (y las terminaciones de microtúbulos) se encuentran en los botones sinápticos del axón y parecen estar involucradas en la afectación de la intensidad de las sinapsis. Esto podría ocurrir por medio de los filamentos de actina en las espinas dendríticas.
Tales espinas aparecen en muchas sinapsis y, aparentemente, pueden crecer o contraerse o sufrir algún otro cambio en su naturaleza. Tales cambios pueden ser inducidos por alteraciones en la actina que hay en su interior —la actina es un constituyente esencial del mecanismo de la contracción muscular—. Los microtúbulos vecinos podrían influir fuertemente en esta actina que, a su vez, podría influir en la forma o las propiedades dieléctricas de la conexión sináptica. Existen al menos otras dos formas diferentes en las que los microtúbulos podrían estar implicados e influir en las intensidades de las sinapsis. Ciertamente están implicados en el transporte de sustancias químicas neurotransmisoras que transportan la señal de una neurona a la siguiente. Son los microtúbulos los que las llevan a lo largo de los axones y dendritas y, de este modo, su actividad influiría en la concentración de dichas sustancias químicas en el extremo del axón y las dendritas. Esto, a su vez, podría influir en la intensidad de la sinapsis. Otra influencia del microtúbulo podría manifestarse en el crecimiento y la degeneración neuronal, al alterar la propia red de conexiones neuronales.
¿Qué son los microtúbulos? En la figura 3.18 se muestra un esbozo de uno de ellos.
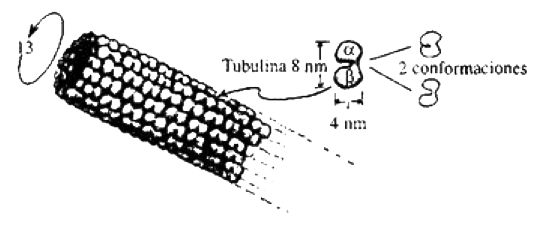
Figura 3.18. Un microtúbulo es un tubo hueco, que consiste normalmente en trece columnas de dímeros de tubulina. Cada molécula de tubulina parece ser susceptible de (al menos) dos conformaciones.
Son pequeños tubos hechos de proteínas llamadas tubulinas. Son interesantes en varios aspectos. Las proteínas de tubulina parecen tener (al menos) dos estados, o conformaciones, diferentes, y pueden cambiar de una conformación a la otra. Aparentemente, pueden ser enviados mensajes a lo largo de los tubos. De hecho, Stuart Hameroff y sus colegas tienen ideas interesantes sobre el modo de enviar señales a lo largo de los tubos. Según Hameroff, los microtúbulos pueden comportarse como autómatas celulares y a lo largo de ellos pueden ser enviadas señales complicadas. Consideremos las dos conformaciones diferentes de cada tubulina como algo que representa los «0» y los «1» de un ordenador digital. Así, un único microtúbulo podría por sí solo comportarse como un ordenador, y tenemos que tener esto en cuenta si estamos considerando lo que hacen las neuronas. Cada neurona no solo se comporta como un interruptor sino que, más bien, implica muchos, muchos microtúbulos, y cada microtúbulo podría estar haciendo cosas muy complicadas.
Aquí es donde entran mis propias ideas. Pudiera ser que la mecánica cuántica sea importante para comprender estos procesos. Una de las cosas que más me interesa de los microtúbulos es que son tubos. Al ser tubos, existe una posibilidad razonable de que sean capaces de aislar lo que está sucediendo en su interior frente a la actividad aleatoria en el entorno. En el capítulo 2 afirmé que necesitamos alguna forma nueva de física RO y, si esta nueva física va a ser relevante, debe haber movimientos de masas en superposiciones cuánticas que estén bien aislados del entorno. Muy bien pudiera ocurrir que, dentro de los tubos, se produzca algún tipo de actividad cuántica coherente a gran escala, algo parecido a un superconductor. Un movimiento de masa significativo estaría involucrado solo cuando su actividad empezara a acoplarse a las conformaciones de tubulina (tipo Hameroff) y entonces el comportamiento de autómata celular estaría en sí mismo sometido a superposición cuántica. El tipo de situaciones que podrían tener lugar se ilustra en la figura 3.19.
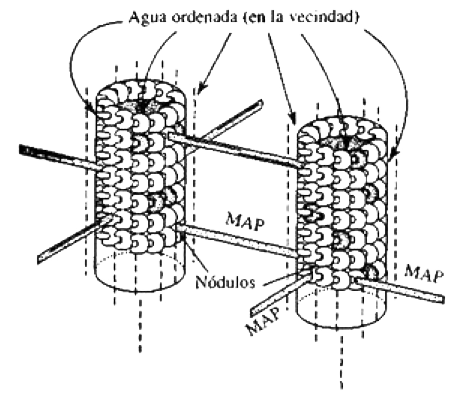
Figura 3.19. sistemas de microtúbulos dentro de (colecciones de) neuronas podrían mantener actividad cuántica coherente a gran escala, y las ocurrencias RO individuales constituirían sucesos conscientes. Se necesita un aislamiento eficaz para esta actividad, posiblemente por agua ordenada que rodea los microtúbulos. Un sistema de interconexiones microtúbulos-proteinas adecuadas (MAP) podría sintonizar esta actividad, fijando los microtúbulos en nódulos.
Como parte de esta imagen tendría que haber algún tipo de oscilación cuántica coherente que ocurriera dentro de los tubos y que necesitara extenderse sobre áreas muy amplias del cerebro. Hace bastantes años, Herbert Frohlich presentó algunas sugerencias generales de este tipo, dando alguna plausibilidad al hecho de que elementos de esta naturaleza pudieran formar parte de los sistemas biológicos. Los microtúbulos parecen ser un buen candidato para las estructuras dentro de las cuales podría tener lugar esta actividad coherente cuántica a gran escala. Cuando utilizo el término gran escala, deben recordar ustedes que en el capítulo 2 describí el enigma EPR y los efectos de la no-localidad cuántica que muestran que efectos que están ampliamente separados no pueden ser considerados independientes entre sí. Efectos no-locales como este ocurren en mecánica cuántica y no pueden entenderse en términos de hechos separados unos de otros: está teniendo lugar algún tipo de actividad global.
Creo que la consciencia es algo global. Por consiguiente, cualquier proceso físico responsable de la consciencia tendría que presentar un carácter esencialmente global. La coherencia cuántica es idónea a este respecto. Para que sea posible semejante coherencia cuántica a gran escala, necesitamos un alto grado de aislamiento, tal como el que podrían suministrar las paredes de los microtúbulos. Sin embargo, también necesitamos algo más cuando empiezan a involucrarse las conformaciones de tubulina. Este necesario aislamiento adicional del entorno podría ser proporcionado por agua ordenada en el exterior inmediato de los microtúbulos. El agua ordenada (que se sabe que existe en células vivas) sería también probablemente un ingrediente importante de cualquier oscilación coherente cuántica que tuviera lugar dentro de los tubos. Aunque es bastante pedir, quizá no sea totalmente irrazonable que todo esto pudiera darse.
Las oscilaciones cuánticas dentro de los tubos tendrían que estar acopladas de alguna forma con la acción de los microtúbulos, a saber, la actividad de autómata celular de la que habla Hameroff; pero ahora su idea tiene que combinarse con la mecánica cuántica. Así pues, debemos tener, no solo actividad computacional en el sentido ordinario, sino también computación cuántica que implica superposiciones de diferentes acciones de este tipo. Si esa fuera toda la historia, aún seguiríamos en el nivel cuántico. En un cierto momento, el estado cuántico podría enmarañarse con el entorno. Entonces saltaríamos al nivel clásico de una forma aparentemente aleatoria, de acuerdo con el procedimiento r usual de la mecánica cuántica. Esto no es bueno si queremos que intervenga una no-computabilidad genuina. Para ello tienen que manifestarse los aspectos no-computables de RO, y eso requiere un aislamiento excelente. Por ello, afirmo que necesitamos algo en el cerebro que tenga un aislamiento suficiente para que la nueva física RO tenga una oportunidad de jugar un papel importante. Lo que necesitaríamos es que estas computaciones microtubulares superpuestas, una vez que se ponen en marcha, estuvieran suficientemente aisladas para que esta nueva física entrara realmente en juego.
Por eso, la imagen que yo tengo es que, durante algunos instantes, estas computaciones cuánticas continúan y permanecen aisladas del resto del material el tiempo suficiente —quizá algo del orden de casi un segundo— para que criterios del tipo de los que estoy hablando dominen sobre los procedimientos cuánticos estándar, intervengan los ingredientes no computacionales y obtengamos algo esencialmente diferente de la teoría cuántica estándar.
Por supuesto, hay mucha especulación en muchas de estas ideas. Pese a todo, ofrecen una posibilidad genuina de una imagen mucho más específica y cuantitativa de la relación entre la consciencia y los procesos biológicos que la que han suministrado otros enfoques. Podemos al menos empezar a hacer un cálculo de cuántas neuronas tendrían que estar involucradas para que esta acción RO pudiera llegar a ser relevante. Lo que se necesita es alguna estimación de T, la escala de tiempo de la que hablé hacia el final del capítulo 2. En otras palabras, suponiendo que los sucesos conscientes están relacionados con tales ocurrencias RO, ¿cuál estimamos que es T? ¿Cuánto tiempo requiere la consciencia? Hay dos tipos de experimentos, ambos asociados con Libet y sus asociados, que resultan relevantes para estas ideas. Uno de ellos trata con el libre albedrío, o consciencia activa; el otro trata con la sensación, o la consciencia pasiva.
Primero, consideremos el libre albedrío. En los experimentos de Libet y Kornhuber se le pide a un sujeto que presione un botón en un instante enteramente dejado a su voluntad. Se colocan electrodos en la cabeza del sujeto para detectar la actividad eléctrica del cerebro. Se hacen muchas pruebas repetidas y los resultados se promedian (figura 3.20.a). El resultado global es que existe algún indicio claro de tal actividad eléctrica aproximadamente un segundo antes del instante en que el sujeto cree que toma la decisión real. Por ello, la libre voluntad parece implicar algún tipo de retardo temporal, del orden de un segundo.
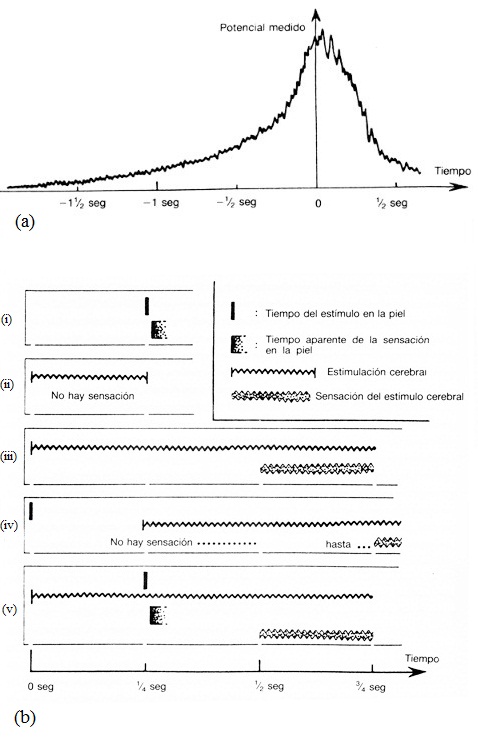
Figura 3.20.
(a) Experimento de Kornhuber, posteriormente repetido y refinado por Liber y sus colegas. La decisión de flexionar el dedo parece tomarse en el instante 0, pero la señal precursora (promediada sobre muchos ensayos) sugiere un preconocimiento de la intención de flexionar.
(b) Experimento de Libet. (i) El estímulo de la piel parece ser percibido aproximadamente en el momento real del estímulo. (ii) Un estímulo cortical de menos de medio segundo no es percibido. (iii) Un estímulo cortical de más de un segundo es percibido a partir de medio segundo en adelante. (iv) Tal estímulo subcortical puede enmascarar retroactivamente un estímulo previo en la piel, lo que indica que la consciencia del estímulo aún no había tenido lugar realmente en el momento del estímulo subcortical. (v) Si un estímulo en la piel se aplica inmediatamente después de semejante estímulo cortical, entonces la consciencia dérmica es remitida hacia atrás pero la consciencia cortical no lo es.
Más notables son los experimentos pasivos, que son más difíciles de realizar. Parecen sugerir que se necesita aproximadamente medio segundo de actividad en el cerebro antes de que una persona llegue a ser pasivamente consciente de algo (figura 3.20.b). En estos experimentos existen formas de bloquear la experiencia consciente de un estímulo en la piel, ¡hasta, aproximadamente, medio segundo después de que este estímulo haya ocurrido realmente! En aquellos casos en los que el procedimiento de bloqueo no se efectúa, el sujeto cree que la experiencia del estímulo en la piel ha ocurrido en el instante real de dicho estímulo. Pese a todo, podría haber sido bloqueado incluso medio segundo después del instante real del estímulo.
Estos son experimentos muy intrigantes, en especial cuando se consideran conjuntamente. Sugieren que la voluntad consciente parece necesitar aproximadamente un segundo, y que la sensación consciente necesita aproximadamente medio segundo. Si imaginamos que la consciencia es algo que hace algo, entonces se nos presenta casi una paradoja. Necesitamos medio segundo antes de hacernos conscientes de algún suceso. Entonces tratamos de invocar a nuestra consciencia para hacer algo con ella. Necesitamos otro segundo para que nuestra libre voluntad haga ese algo. En resumen, necesitamos aproximadamente un total de un segundo y medio. Por eso, si algo requiere una respuesta conscientemente voluntaria, necesitaríamos aproximadamente un segundo y medio antes de que realmente pudiéramos hacer uso de ella. Personalmente encuentro eso bastante difícil de creer. Consideremos, por ejemplo, la conversación ordinaria. Creo que, aunque buena parte de la conversación podría ser automática e inconsciente, el hecho de que se necesite un segundo y medio para dar una respuesta consciente me parece muy extraño.
Yo considero esto como indicio de que muy bien podría haber algo en nuestra forma de interpretar tales experimentos que presuponga que la física que estamos utilizando es básicamente física clásica. Recordemos el problema de comprobación de bombas donde hablábamos de hechos contrafácticos y el hecho de que los sucesos contrafácticos pudieran tener influencia sobre cosas, incluso si no ocurrieron realmente.
El tipo ordinario de lógica que utilizamos tiende a fallar si no somos cuidadosos. Tenemos que tener en cuenta cómo se comportan los sistemas cuánticos, y podría suceder que algo curioso esté ocurriendo en estas medidas de tiempo debido a la no-localidad cuántica y los hechos contrafácticos cuánticos. Es muy difícil entender la no-localidad cuántica dentro del marco de la teoría especial de la relatividad. Mi opinión personal es que, para comprender la no-localidad cuántica, necesitaremos una teoría radicalmente nueva. Esta nueva teoría no será simplemente una ligera modificación de la mecánica cuántica sino algo tan diferente de la mecánica cuántica estándar como la teoría general de la relatividad es diferente de la gravedad newtoniana. Tendría que ser algo con un marco conceptual completamente diferente. En esta imagen, la no-localidad cuántica estaría incorporada en la teoría.
En el capítulo 2 se mostró que la no-localidad es algo que, aunque muy enigmático, puede describirse matemáticamente. Permítanme mostrarles la imagen de un triángulo imposible en la figura 3.21.
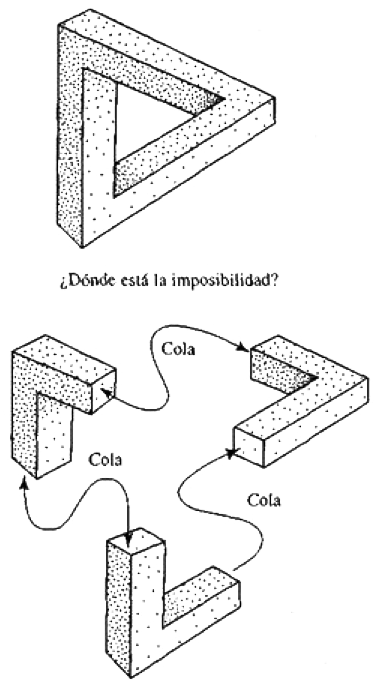
Figura 3.21. Triángulo imposible. La imposibilidad no puede localizarse; pese a todo, puede definirse en términos matemáticos precisos como una abstracción de las reglas de encolado subyacentes a su construcción.
Ustedes podrían preguntarse: «¿Dónde está la imposibilidad?». ¿Pueden ustedes localizarla? Ustedes pueden tapar partes diversas de la imagen y, sea cual sea el fragmento del triángulo que tapen, la imagen se hace repentinamente posible. Por eso ustedes no pueden decir que la imposibilidad está en algún lugar concreto en la imagen: la imposibilidad es una característica de la estructura completa. De todos modos, existen formas matemáticas precisas para hablar de tales cosas. Esto puede hacerse descomponiendo la imagen, volviéndola a encolar y extrayendo ciertas ideas matemáticas abstractas de la estructura global y detallada del encolado. La noción de cohomología es la noción apropiada en este caso. Esta noción nos proporciona un medio de calcular el grado de imposibilidad de esta figura. Este es el tipo de matemática no-local que muy bien podría estar implicada en nuestra nueva teoría.
¡No hay que suponer que sea un accidente el que la figura 3.21 se parezca a la figura 3.3! El dibujo de la figura 3.3 fue realizado deliberadamente para resaltar un elemento de paradoja. Hay algo característicamente misterioso en la forma en que estos tres mundos se interrelacionan —en donde cada uno de ellos parece casi emerger de una pequeña parte de su predecesor—. Pese a todo, como sucede con la figura 3.21, con comprensión adicional quizá seamos capaces de entender o incluso resolver parte de este misterio. Es importante reconocer los rompecabezas y los misterios cuando se presentan. Pero el solo hecho de que suceda algo muy enigmático no significa que nunca seremos capaces de comprenderlo.