
Figura 1.1.
El título de este libro es Lo grande, lo pequeño y la mente humana, y el tema de este primer capítulo es lo grande. Los capítulos 1 y 2 están dedicados a nuestro Universo físico, que voy a representar muy esquemáticamente mediante la esfera de la figura 1.1. Sin embargo, en ellos no se va a describir con detalle qué es lo que hay en uno u otro lugar de nuestro Universo, sino más bien quiero concentrarme en la comprensión de las leyes reales que rigen el comportamiento del mundo.

Figura 1.1.
Una de las razones por las que he decidido dividir las descripciones de las leyes físicas en dos capítulos: lo grande y lo pequeño, es que las leyes que determinan el comportamiento del mundo a gran escala y las que rigen su comportamiento a pequeña escala parecen muy diferentes. El hecho de que parezcan ser tan diferentes, y de que quizá tengamos algo que ver con esta aparente discrepancia, es fundamental para el tema del capítulo 3, y aquí es donde interviene la mente humana.
Dado que voy a hablar acerca del mundo físico en términos de las teorías físicas que subyacen a su comportamiento, también tendré que decir algo sobre otro mundo, el mundo platónico de las ideas y, concretamente, sobre su papel como mundo de la verdad matemática. Uno puede muy bien adoptar el punto de vista de que el mundo platónico contiene otras ideas, tales como la Bondad y la Belleza, pero aquí solo me interesaré por los conceptos platónicos de las matemáticas. Para algunas personas resulta difícil concebir que este mundo tenga una existencia independiente. Preferirán considerar los conceptos matemáticos como meras idealizaciones de nuestro mundo físico y, desde esta perspectiva, el mundo matemático se concebiría como algo que emerge del mundo de los objetos físicos (figura 1.2).
Figura 1.2.
Pero no es así como yo concibo las matemáticas, ni creo que la mayoría de los matemáticos y los físicos matemáticos tengan esa idea del mundo. Lo conciben de un modo bastante diferente, como una estructura gobernada de manera precisa y de acuerdo con leyes matemáticas intemporales. Por eso encuentran más apropiado considerar el mundo físico como algo que emerge del intemporal mundo de las matemáticas, tal como se ilustra en la figura 1.3. Esta imagen tendrá importancia en el tema del capítulo 3, y también subyace a mucho de lo que diré en los capítulos 1 y 2.
Figura 1.3.
Uno de los aspectos más importantes sobre el comportamiento del Universo es que parece estar basado en las matemáticas hasta un grado de precisión extraordinario. Cuanto mejor entendemos el mundo físico, y más profundamente sondeamos en las leyes de la naturaleza, más nos parece que la realidad física se evapora hasta que nos quedamos solo con las matemáticas. Cuanto mejor entendemos las leyes de la física, más nos vemos abocados a este ámbito de las matemáticas y de los conceptos matemáticos.
Observemos las escalas con las que tenemos que tratar en el Universo y también el papel de nuestro lugar en él. Puedo resumir todas estas escalas en un único diagrama (figura 1.4).
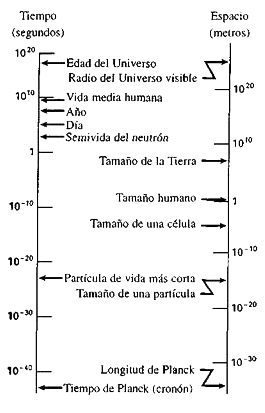
Figura 1.4. Escalas de tamaño y de tiempo en el Universo.
En el lado izquierdo se muestran las escalas de tiempo y en el lado derecho están las correspondientes escalas de distancias. En la parte inferior del diagrama, a la izquierda, se encuentra la escala de tiempo más corta que tiene sentido físico. Esta escala de tiempo es de, aproximadamente, 10−43 segundos y suele conocerse como escala de tiempo de Planck o cronón. Este intervalo de tiempo es mucho más corto que cualquier otro fenómeno experimentado en la física de partículas. Por ejemplo, las partículas de vida más corta, llamadas resonancias, existen durante unos 10−23 segundos. Más arriba en el diagrama, a la izquierda, se muestran el día y el año y, en la parte superior, la edad actual del Universo.
En el lado derecho del gráfico aparecen las distancias correspondientes a estas escalas de tiempo. La longitud que corresponde a la escala de tiempo de Planck (un cronón) es la unidad fundamental de longitud, llamada longitud de Planck. Los conceptos de tiempo y de longitud de Planck aparecen de forma natural cuando tratamos de combinar las teorías físicas que describen lo grande y las que definen lo pequeño, o, lo que es lo mismo, combinar la teoría general de la relatividad de Einstein, que se ocupa de la física de lo muy grande, con la mecánica cuántica, que describe la física de lo muy pequeño. Cuando se unen estas teorías, estas longitudes y tiempos de Planck resultan ser fundamentales. La traducción desde el eje izquierdo hasta el eje derecho del diagrama se hace mediante la velocidad de la luz, de modo que los tiempos pueden traducirse en distancias preguntando a qué distancia podría viajar una señal luminosa en ese intervalo temporal.
Los tamaños de los objetos físicos representados en el diagrama abarcan desde 10−15 metros (el tamaño característico de las partículas) hasta 1027 metros (el radio del Universo observable en la actualidad, que es aproximadamente la edad del Universo multiplicada por la velocidad de la luz). Resulta curioso advertir el lugar donde nos encontramos nosotros en el diagrama, la escala humana. Puede verse que, con respecto a las dimensiones espaciales, estamos más o menos en el centro de la gráfica. Somos enormes comparados con la longitud de Planck; incluso si se nos compara con el tamaño de las partículas somos muy grandes. Pese a todo, en la escala de distancias del Universo observable somos minúsculos. De hecho, somos mucho más pequeños comparados con esta escala que grandes comparados con las partículas. Por otro lado, con respecto a las dimensiones temporales, ¡el tiempo de una vida humana es casi tan largo como el del Universo!
Es habitual hablar de la naturaleza efímera de la existencia pero, cuando se considera la duración de una vida humana tal como se muestra en el diagrama, puede comprobarse que esta no es en absoluto breve: ¡vivimos más o menos tanto como el propio Universo! Por supuesto, esto solo es cierto mirando a escala logarítmica, pero eso es lo más práctico cuando estamos interesados en rangos tan enormes. Para decirlo de otro modo, el número de veces que la duración de una vida humana iguala la edad del Universo es muchísimo menor que el número de tiempos de Planck, o incluso de vidas medias de las partículas de vida más corta, que equivalen a una vida humana. Así pues, somos estructuras muy estables en el Universo. Por lo que se refiere a los tamaños espaciales, estamos prácticamente en el medio: no experimentamos directamente ni la física de lo muy grande ni la de lo muy pequeño. Estamos exactamente entre ambas. De hecho, en una escala logarítmica, todos los seres vivos, desde las simples células hasta los árboles y las ballenas, están aproximadamente en el mismo tamaño intermedio.
¿Qué tipo de física se aplica en estas escalas diferentes? Permítanme introducir el diagrama que resume el conjunto de la física (figura 1.5). Por supuesto, he tenido que dejar fuera algunos detalles, como son ¡todas las ecuaciones! Pero están indicadas las teorías básicas esenciales que utilizan los físicos.

Figura 1.5.
El punto clave es que, en física, utilizamos dos tipos de procedimientos muy diferentes. Para describir el comportamiento a pequeña escala utilizamos la mecánica cuántica, que he descrito como el nivel cuántico en la figura 1.5. Se acusa a la mecánica cuántica de ser poco nítida e indeterminista, pero esto no es cierto. Mientras permanezcamos en este nivel, la teoría cuántica es determinista y precisa. En su forma más familiar, la mecánica cuántica implica el uso de la ecuación conocida como ecuación de Schrödinger, que rige el comportamiento del estado físico de un sistema cuántico —lo que se denomina su estado cuántico— y esta es una ecuación determinista. He utilizado la letra U para describir esta actividad en el nivel cuántico. La indeterminación en mecánica cuántica aparece solo cuando realizamos lo que se denomina hacer una medida y eso implica amplificar un suceso desde el nivel cuántico al nivel clásico. Posteriormente, en el capítulo 2, ampliaré estas ideas.
A gran escala utilizamos la física clásica, que es completamente determinista; estas leyes clásicas incluyen las leyes del movimiento de Newton; las leyes de Maxwell para el campo electromagnético, que incorporan la electricidad, el magnetismo y la luz; y las teorías de la relatividad de Einstein, la teoría especial, que trata con velocidades grandes, y la teoría general, que trata con campos gravitatorios grandes. Estas leyes se aplican de forma muy exacta a gran escala.
Solo como una nota a la figura 1.5, se puede ver que he incluido un comentario sobre computabilidad en física cuántica y clásica. Esto no tiene relevancia en este capítulo ni en el capítulo 2, pero sí la tendrá en el capítulo 3, y allí volveré a la cuestión de la computabilidad.
En el resto de este capítulo me interesaré principalmente por la teoría de la relatividad de Einstein: en concreto, por el funcionamiento de la teoría, su extraordinaria precisión y algo sobre su elegancia como teoría física. Pero consideremos primero la teoría newtoniana.
La física de Newton permite, como la relatividad, utilizar una descripción espacio-temporal. Esta fue formulada de forma precisa por primera vez por Cartan para la teoría de la gravedad de Newton, algún tiempo después de que Einstein hubiera presentado su teoría general de la relatividad. La física de Galileo y Newton se representa en un espacio-tiempo para el que existe una coordenada de tiempo global, que aquí se muestra dirigida hacia la parte superior del diagrama (figura 1.6).
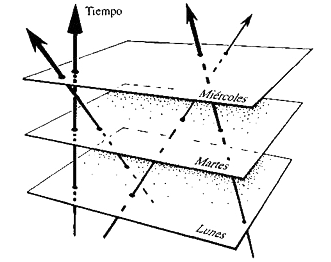
Figura 1.6. Espacio-tiempo galileano: las partículas en movimiento uniforme se representan por líneas.
Para cada valor constante del tiempo, existe una sección espacial que es un espacio tridimensional euclidiano, aquí representado como un plano horizontal. Una característica esencial de la imagen del espacio-tiempo newtoniano es que estos cortes espaciales, a través del diagrama, representan momentos de simultaneidad.
Así pues, todo lo que ocurre el lunes a mediodía yace en un corte horizontal a través del diagrama espacio-temporal; todo lo que sucede el martes a mediodía yace en el siguiente corte mostrado en el diagrama, y así sucesivamente. El tiempo cruza el diagrama espacio-temporal y las secciones euclidianas se suceden una tras otra a medida que el tiempo avanza. Todos los observadores, independientemente de cómo se muevan a través del espacio-tiempo, pueden ponerse de acuerdo acerca del instante en el que ocurren los sucesos, porque todos utilizan los mismos cortes temporales para medir el paso del tiempo.
En la teoría especial de la relatividad de Einstein tenemos que adoptar una imagen diferente. En dicha teoría, la imagen espacio-temporal es absolutamente esencial: la diferencia clave es que el tiempo ya no tiene el carácter universal que posee en la teoría newtoniana. Para apreciar la diferencia entre ambas teorías es necesario entender una parte esencial de la teoría de la relatividad, a saber, aquellas estructuras conocidas como conos de luz.
¿Qué es un cono de luz? Un cono de luz está dibujado en la figura 1.7. Imaginemos un destello de luz que tiene lugar en cualquier punto y en algún instante —es decir, en un suceso en el espacio-tiempo— y las ondas luminosas que viajan hacia fuera a partir de este suceso, la fuente del destello, a la velocidad de la luz.
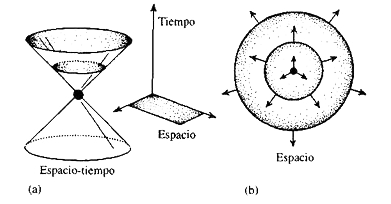
Figura 1.7. Representación de la historia de un destello luminoso en términos de propagación en (a) el espacio-tiempo y (b) el espacio.
En una imagen puramente espacial (figura 1.7.b), podemos representar las trayectorias de las ondas luminosas en el espacio como una esfera que se expande a la velocidad de la luz. Ahora podemos traducir este movimiento de las ondas luminosas en un diagrama espacio-temporal (figura 1.7.a) en el que el tiempo corre hacia la parte superior del diagrama y las coordenadas espaciales se refieren a desplazamientos horizontales, lo mismo que sucedía en la situación newtoniana de la figura 1.6. Por desgracia, en la imagen espacio-temporal completa (figura 1.7.a) solo podemos representar dos dimensiones espaciales horizontalmente en el diagrama, porque el espacio-tiempo de nuestra imagen es solo tridimensional. Ahora vemos que el destello está representado por un punto (suceso) en el origen y que las trayectorias subsiguientes de los rayos luminosos (ondas) intersectan los planos espaciales horizontales en círculos cuyos radios aumentan hacia la parte superior del diagrama a la velocidad de la luz. Puede verse que las trayectorias de los rayos luminosos forman conos en el diagrama espacio-temporal. El cono de luz representa así la historia de este destello luminoso: la luz se propaga desde el origen a lo largo del cono de luz, lo que significa a la velocidad de la luz, hacia el futuro. Los rayos luminosos también pueden llegar al origen a lo largo del cono de luz del pasado —esa parte del cono de luz se conoce como el cono de luz pasado y toda información llevada al observador por las ondas luminosas llega al origen a lo largo de este cono—.
Los conos de luz describen las estructuras más importantes del espacio-tiempo. En particular, representan los límites de la influencia causal. La historia de una partícula en el espacio-tiempo se representa por una línea que viaja hacia arriba en el diagrama espacio-temporal, y esta línea tiene que estar dentro del cono de luz (figura 1.8). Esta es simplemente otra forma de decir que una partícula material no puede viajar más rápido que la luz. Ninguna señal puede viajar desde el interior al exterior del cono de luz futuro y, por eso, el cono de luz representa los límites de la causalidad.
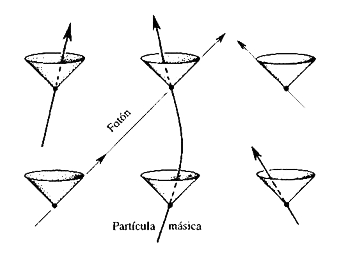
Figura 1.8. Ilustración del movimiento de una partícula en el espacio-tiempo de la relatividad especial, que se conoce como espacio-tiempo de Minkowski o geometría de Minkowski. Los conos de luz en los diferentes puntos del espacio-tiempo están alineados y las partículas solo pueden viajar en el interior de sus conos de luz futuros.
Existen algunas propiedades geométricas significativas en relación con los conos de luz. Consideremos dos observadores que se mueven a velocidades diferentes en el espacio-tiempo. A diferencia del caso de la teoría newtoniana, donde los planos de simultaneidad son los mismos para todos los observadores, no hay simultaneidad absoluta en la relatividad. Los observadores que se mueven a velocidades diferentes dibujan sus propios planos de simultaneidad como secciones diferentes en el espacio-tiempo, como se ilustra en la figura 1.9.
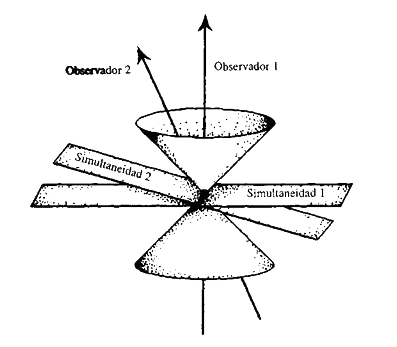
Figura 1.9. Ilustración de la relatividad de la simultaneidad según la teoría especial de la relatividad de Einstein. Los observadores 1 y 2 están en movimiento uno con respecto al otro en el espacio-tiempo. Sucesos que son simultáneos para el observador 1 no son simultáneos para el observador 2 y viceversa.
Hay una forma perfectamente definida de pasar desde un plano a otro mediante lo que se conoce como una transformación de Lorentz, y estas transformaciones constituyen lo que se denomina el grupo de Lorentz. El descubrimiento de este grupo fue un ingrediente esencial en el hallazgo de la teoría especial de la relatividad de Einstein. El grupo de Lorentz puede entenderse como un grupo de transformaciones (lineales) espacio-temporales que dejan invariante un cono de luz.
También podemos apreciar el grupo de Lorentz desde un punto de vista ligeramente diferente. Como he resaltado, los conos de luz son las estructuras fundamentales del espacio-tiempo. Imaginen un observador situado en algún lugar en el espacio, mirando al Universo. Lo que ese observador ve son los rayos de luz que proceden de las estrellas y entran en sus ojos. Según el punto de vista espacio-temporal, los sucesos que observa son las intersecciones de las líneas-de-universo de las estrellas con su cono de luz pasado, como se ilustra en la figura 1.10.a.
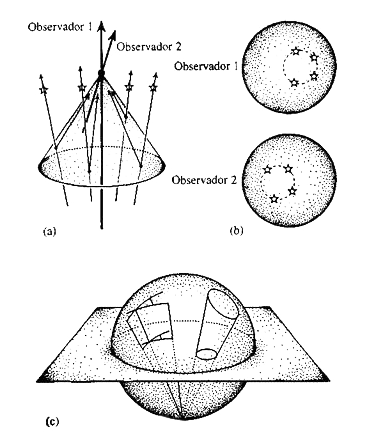
Figura 1.10. Ilustración de las observaciones celestes hechas por los observadores 1 y 2.
(a) Los observadores 1 y 2 ven estrellas a lo largo del cono de luz pasado. Los puntos donde las estrellas cortan el cono de luz se indican por puntos negros. Las señales luminosas se propagan desde las estrellas hasta los observadores a lo largo del cono de luz tal como se ilustra. El observador 2 se mueve en el espacio-tiempo a cierta velocidad con respecto al observador 1.
(b) Ilustración de la posición de las estrellas en el cielo tal como las ven el observador 1 y el observador 2 cuando coinciden en un mismo punto del espacio-tiempo.
(c) Una buena manera de representar la trasformación del cielo de un observador a otro es mediante una proyección estereográfica: los círculos se transforman en círculos y los ángulos se conservan.
Observen a lo largo de su cono de luz pasado las posiciones de las estrellas en puntos concretos. Dichos puntos parecen estar situados en la esfera celeste que le rodea. Situemos ahora otro observador, que se mueve a alta velocidad con respecto al primero, y que pasa muy cerca de él en el momento en que ambos miran al cielo. Este segundo observador percibe las mismas estrellas que el primero, pero encuentra que están situadas en posiciones diferentes en la esfera celeste (figura 1.10.b) —este es el efecto conocido como aberración—. Existe un conjunto de transformaciones que nos permite calcular la relación entre lo que cada uno de estos observadores ve en su esfera celeste. Individualmente, estas transformaciones hacen corresponder una esfera a otra esfera. Pero es una transformación de un tipo muy especial. Transforma círculos exactos en círculos exactos y conserva los ángulos. Así, si una figura en el cielo parece un círculo para el primer observador, entonces también debe parecer un círculo para el otro observador.
Existe una manera muy bella de describir cómo funciona esto y la ilustro para mostrar que hay una elegancia particular en las matemáticas que suelen subyacer a la física en el nivel más fundamental. La figura 1.10.c muestra una esfera con un plano dibujado que pasa por su ecuador. Podemos dibujar figuras en la superficie de la esfera y luego examinar cómo se proyectan en el plano ecuatorial desde el polo sur, tal como se ilustra. Este tipo de proyección se conoce como proyección estereográfica y tiene algunas propiedades bastante extraordinarias. Círculos en la esfera se proyectan en círculos exactos en el plano, y los ángulos que forman entre sí curvas en la esfera se proyectan en ángulos exactamente iguales en el plano. Como discutiré más extensamente en el capítulo 2 (compárese con la figura 2.4), esta proyección nos permite etiquetar los puntos de la esfera mediante números complejos (números que incluyen la raíz cuadrada de −1), números que también se utilizan para etiquetar los puntos del plano ecuatorial, junto con el infinito, para conferir a la esfera la estructura conocida como esfera de Riemann.
Para aquellos que estén interesados, la transformación de aberración es:
y, como es bien conocido para los matemáticos, esta función transforma círculos en círculos y conserva los ángulos. Las funciones de este tipo se conocen como transformaciones de Möbius. Para nuestros propósitos presentes, simplemente necesitamos señalar la admirable sencillez de la fórmula (de aberración) de Lorentz cuando se escribe en términos de un parámetro complejo u.
Un punto sorprendente acerca de esta forma de considerar dichas transformaciones es que, según la teoría especial de la relatividad, la fórmula es muy sencilla, mientras que, si expresáramos la correspondiente transformación de aberración según la mecánica newtoniana, la fórmula sería mucho más complicada. A menudo resulta que, cuando descendemos a los fundamentos y desarrollamos una teoría más exacta, las matemáticas resultan ser más sencillas, incluso si la apariencia formal es más complicada en primera instancia. Este punto importante queda ejemplificado en el contraste entre la teoría de la relatividad de Galileo y la de Einstein.
Así pues, en la teoría especial de la relatividad tenemos una teoría que, en muchos aspectos, es más sencilla que la mecánica newtoniana. Desde el punto de vista de las matemáticas, y en particular desde el punto de vista de la teoría de grupos, es una estructura mucho más amable. En la teoría especial de la relatividad, el espacio-tiempo es plano y todos los conos de luz están alineados regularmente, tal como se ilustra en la figura 1.8. Ahora bien, si damos un paso más allá hasta la teoría general de la relatividad de Einstein, es decir, la teoría del espacio-tiempo que tiene en cuenta la gravedad, la imagen parece a primera vista bastante retorcida: los conos de luz son un caos (figura 1.11).
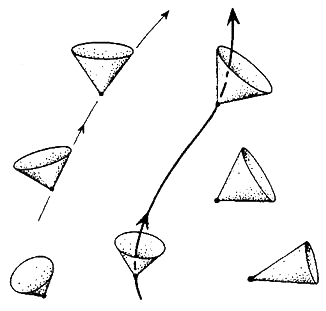
Figura 1.11. Una imagen del espacio-tiempo curvo.
Con todo, he venido señalando que, a medida que desarrollamos teorías cada vez más evolucionadas, las matemáticas se hacen más simples. Pero veamos lo que ha sucedido aquí: yo tenía una porción muy elegante de las matemáticas que se ha hecho horriblemente complicada. Este tipo de cosas sucede, ustedes tendrán que seguir conmigo algún tiempo hasta que reaparezca la simplicidad.
Permítanme recordarles los ingredientes fundamentales de la teoría de la gravedad de Einstein. Un ingrediente básico se denomina principio de equivalencia de Galileo. En la figura 1.12.a muestro a Galileo inclinado en lo alto de la Torre de Pisa y dejando caer piedras grandes y pequeñas.
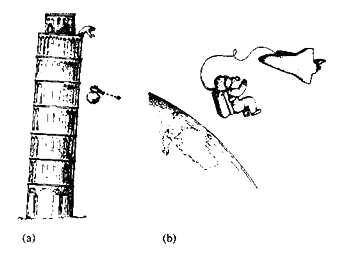
Figura 1.12.
(a) Galileo arrojando dos piedras (y una videocámara) desde la Torre inclinada de Pisa.
(b) El astronauta observa que el vehículo espacial se mantiene frente a él, aparentemente sin ser afectado por la gravedad.
Ya hiciera o no realmente este experimento, Galileo comprendió muy bien que, si se ignoran los efectos de la resistencia del aire, las dos piedras llegarán al suelo en el mismo instante. Si uno de ustedes estuviera sentado en una de estas piedras mirando a la otra mientras caen juntas, observaría que la otra piedra se mantiene frente a él (he situado una videocámara fijada a una de las piedras para realizar la observación). Hoy día, con los viajes espaciales, este es un fenómeno muy familiar —recientemente hemos visto un astronauta de origen inglés paseando por el espacio— y, como sucede con la piedra grande y la piedra pequeña, la nave espacial se mantiene junto al astronauta —este es exactamente el mismo fenómeno que el principio de equivalencia de Galileo—.
Así, si se considera la gravedad de la forma correcta, es decir, en un sistema de referencia en caída, esta parece desaparecer directamente ante nuestros ojos. Esto es, de hecho, correcto; pero la teoría de Einstein no nos dice que la gravedad desaparezca: solo nos dice que la fuerza de la gravedad desaparece. Queda algo, y ese algo es el efecto de marea de la gravedad.
Permítanme introducir algunos elementos matemáticos más, pero no muchos. Tenemos que describir la curvatura del espacio-tiempo y esto se consigue mediante un objeto conocido como un tensor que yo he denominado Riemann en la siguiente ecuación. En realidad se denomina tensor de curvatura de Riemann, pero yo no les voy a decir qué es, solo que está representado por una R mayúscula con varios índices adheridos a su pie, que se indican por los puntos. El tensor de curvatura de Riemann consta de dos partes. Una de las partes se denomina curvatura de Weyl y la otra, curvatura de Ricci, y tenemos la ecuación (esquemática):
Riemann = Weyl + Ricci
R… = cW… + cR…g…
Formalmente, cW… y cR… son los tensores de curvatura de Weyl y Ricci, respectivamente, y g… es el tensor métrico.
La curvatura de Weyl mide eficazmente el efecto de marea. ¿Qué es el efecto de marea? Recordemos que, desde el punto de vista del astronauta, parece como si la gravedad hubiera sido abolida, aunque esto no es del todo cierto. Imaginemos que el astronauta está rodeado por una esfera de partículas que están inicialmente en reposo con respecto a él. En un primer momento, las partículas se mantienen aproximadamente en sus posiciones pero pronto empezarán a acelerarse debido a las ligeras diferencias en la atracción gravitatoria que ejerce la Tierra en los diferentes puntos de la esfera. (Nótese que estoy describiendo el efecto en lenguaje newtoniano, pero por ahora es suficiente). Estas ligeras diferencias hacen que la esfera original de partículas se distorsione hasta mostrar una configuración elíptica, como se ilustra en la figura 1.13.a.
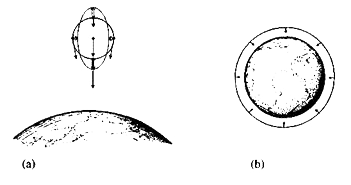
Figura 1.13.
(a) El efecto de marea. Las flechas dobles muestran la aceleración relativa.
(b) Cuando la esfera rodea un cuerpo material (aquí rodea la Tierra) hay una aceleración neta hacia dentro.
Esta distorsión se debe en parte a la atracción ligeramente mayor que ejerce la Tierra sobre aquellas partículas más próximas a ella y la menor atracción que ejerce sobre aquellas que están más alejadas, y en parte también a que, en los lados izquierdo y derecho de la esfera, la atracción de la Tierra actúa ligeramente hacia dentro. Esto hace que la esfera se distorsione y se convierta en un elipsoide. Se denomina efecto de marea por la muy buena razón de que si se reemplaza la Tierra por la Luna y la esfera de partículas por la Tierra con sus océanos, entonces la Luna produce el mismo efecto gravitacional sobre la superficie de los océanos que el que la Tierra produce en la esfera de partículas: la superficie del mar más próxima a la Luna es atraída hacia ella, mientras que la que está en el lado opuesto de la Tierra es, de hecho, empujada lejos de ella. El efecto hace que la superficie del mar se abombe en los lados próximo y lejano de la Tierra y es la causa de las dos mareas altas que ocurren cada día.
Los efectos de la gravedad, desde el punto de vista de Einstein, consisten simplemente en este efecto de marea. Está definido esencialmente por la curvatura de Weyl, es decir, la parte cW… de la curvatura de Riemann. Esta parte del tensor de curvatura conserva el volumen: es decir, si se calculan las aceleraciones iniciales de las partículas de la esfera, el volumen de la esfera y el volumen del elipsoide en el que se transforma son inicialmente iguales.
La parte restante de la curvatura se conoce como curvatura de Ricci y tiene un efecto reductor del volumen. A partir de la figura 1.13.b puede verse que, si en lugar de estar en la parte inferior del diagrama, la Tierra estuviera dentro de la esfera de partículas, el volumen de la esfera de partículas se reduciría a medida que las partículas se aceleraran hacia dentro. La cantidad de esta reducción de volumen es una medida de la curvatura de Ricci. La teoría de Einstein nos dice que esta curvatura en un punto del espacio está determinada por la cantidad de materia presente dentro de una pequeña esfera centrada aproximadamente en dicho punto. En otras palabras, la densidad de materia, adecuadamente definida, en un punto del espacio nos dice cómo se aceleran las partículas hacia dicho punto. La teoría de Einstein es casi la misma que la de Newton cuando se expresa de este modo.
Así es como Einstein formuló su teoría de la gravedad: se expresa en términos de los efectos de marea, que son medidas de la curvatura espacio-temporal local. Es crucial que tengamos que pensar en términos de la curvatura de un espacio-tiempo tetra-dimensional. Esto se mostraba esquemáticamente en la figura 1.11: consideramos las líneas que representan las líneas-de-universo de partículas y las formas en que estas trayectorias son distorsionadas como una medida de la curvatura del espacio-tiempo. Así pues, la teoría de Einstein es esencialmente una teoría geométrica del espacio-tiempo tetradimensional —es una teoría de extraordinaria belleza desde una perspectiva matemática—.
La historia del descubrimiento por Einstein de la teoría general de la relatividad contiene una moraleja importante. Fue formulada en su totalidad por primera vez en 1915. No estaba motivada por ninguna necesidad de describir o explicar ciertas observaciones sino por diversos desiderata estéticos, geométricos y físicos. Los ingredientes clave eran el principio de equivalencia de Galileo, ejemplificado por la caída de piedras de diferentes masas (figura 1.12), y las ideas de la geometría no euclidiana, que es el lenguaje natural para describir la curvatura del espacio-tiempo. No existía un trabajo de observación en 1915. Una vez que la relatividad general estuvo formulada en su forma final, se advirtió que había tres pruebas derivadas de la observación que debían apoyar la teoría. El perihelio de la órbita de Mercurio avanza, o gira, de una forma que no podía ser explicada por la influencia gravitatoria newtoniana de los otros planetas: la teoría general de la relatividad predice exactamente el avance observado. Las trayectorias de los rayos luminosos son curvadas por el Sol, y esta fue la razón de la famosa expedición para observar el eclipse de 1919, dirigida por Arthur Eddington y que encontró un resultado coherente con la predicción de Einstein (figura 1.14.a).
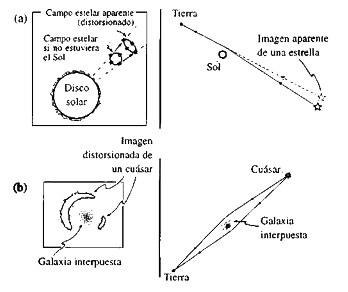
Figura 1.14.
(a) Efectos observacionales directos de la gravedad sobre la luz según la relatividad general. La curvatura de Weyl del espacio-tiempo se manifiesta como una distorsión del campo estelar lejano, en este caso debida al efecto de curvatura de la luz en el campo gravitatorio del Sol. Una figura circular de estrellas se distorsionaria en una figura elíptica.
(b) El efecto de curvatura de la luz de Einstein es ahora una herramienta importante en la astronomia observacional. La masa de la galaxia interpuesta puede ser estimada a partir de la medida de la distorsión que provoca en la imagen de un cuásar lejano.
La tercera prueba era la predicción de que los relojes se hacen más lentos en un potencial gravitatorio: es decir, un reloj próximo al suelo atrasa con respecto a un reloj situado en lo alto de una torre. Este efecto también ha sido medido experimentalmente. Estas nunca fueron, sin embargo, pruebas muy impresionantes: los efectos eran siempre muy pequeños y varias teorías diferentes podrían haber dado los mismos resultados.
Ahora la situación ha cambiado drásticamente: en 1993, Hulse y Taylor recibieron el Premio Nobel por una extraordinaria serie de observaciones. La figura 1.15.a muestra el púlsar binario conocido como PSR 1913+16: consiste en un par de estrellas de neutrones, cada una de las cuales, de enorme densidad, tiene una masa aproximadamente igual a la del Sol pero solo unos pocos kilómetros de diámetro.
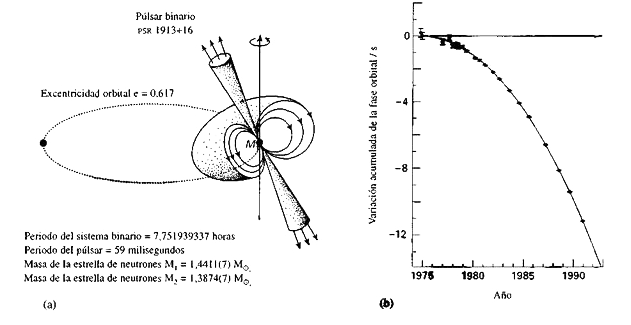
Figura 1.15.
(a) Representación esquemática del púlsar binario PSR 1913+16. Una de las estrellas de neutrones es un púlsar de radio. La señal de radio se emite a lo largo de los polos del dipolo magnético que no está alineado con el eje de rotación de la estrella de neutrones. Se observan pulsos muy precisos cuando el estrecho haz de radiación barre la visual del observador. Las propiedades de las dos estrellas de neutrones han sido obtenidas a partir de un cronometraje muy preciso de los tiempos de llegada de los pulsos utilizando (y verificando) efectos que solo están presentes en la teoría general de la relatividad de Einstein.
(b) El cambio de la fase de los tiempos de llegada de los pulsos procedentes del púlsar binario PSR 1913+16, comparado con el cambio esperado debido a la emisión de radiación gravitatoria por el sistema binario de estrellas de neutrones (línea continua).
Las estrellas de neutrones describen órbitas extremadamente elípticas alrededor de su centro de gravedad común. Una de ellas genera un campo magnético muy intenso que hace que las partículas que son arrastradas a su alrededor emitan una radiación intensa que viaja hasta la Tierra, a unos 30.000 años-luz de distancia, donde es observada como una serie de pulsos bien definidos. Se han realizado todo tipo de observaciones muy precisas de los tiempos de llegada de dichos pulsos. En particular, han podido calcularse todas las propiedades de las órbitas de las dos estrellas de neutrones así como todas las correcciones minúsculas debidas a la teoría general de la relatividad.
Existe, además, una característica que es absolutamente exclusiva de la relatividad general, y que no está presente en ningún caso en la teoría newtoniana de la gravedad: los objetos que están en órbita uno alrededor del otro irradian energía en forma de ondas gravitatorias. Estas son similares a ondas de luz, aunque son ondulaciones en el espacio-tiempo en lugar de ser ondulaciones en el campo electromagnético. Estas ondas absorben energía del sistema a un ritmo que puede ser exactamente calculado según la teoría de Einstein, y este ritmo de pérdida de energía del sistema de estrellas de neutrones binarias coincide muy exactamente con las observaciones, como se ilustra en la figura 1.15.b, que muestra la aceleración del período orbital de las estrellas de neutrones, medida durante 20 años de observación. Estas señales pueden cronometrarse de forma tan precisa que, al cabo de 20 años, se sabe que la teoría es correcta con una precisión equivalente a una parte en 1014. Esto hace de la relatividad general la teoría científica comprobada con más exactitud.
Hay una moraleja en esta historia: las motivaciones de Einstein para dedicar ocho o más años de su vida al desarrollo de la teoría general de la relatividad no eran ni producto de la observación ni de la experimentación. A veces, se argumenta: «Los físicos buscan pautas en sus resultados experimentales y luego encuentran alguna bonita teoría que coincide con ellas. Quizá esto explica por qué las matemáticas y la física trabajan tan bien juntas».
Pero, en este caso, las cosas no fueron así. La teoría fue desarrollada originalmente sin tener que responder a ninguna observación: la teoría matemática es muy elegante y está físicamente muy bien motivada. La cuestión es que la estructura matemática está precisamente allí, en la naturaleza, y la teoría existe realmente allí, en el espacio: no ha sido impuesta a la naturaleza por nadie. Este es uno de los puntos esenciales de este capítulo. Einstein revelaba algo que ya estaba presente. Más aún, no era simplemente algún elemento menor de física lo que descubrió: es lo más fundamental que tenemos en nuestro Universo, la propia naturaleza del espacio y del tiempo.
He aquí un caso muy claro, remite de nuevo a mi diagrama original concerniente a la relación entre el mundo de las matemáticas y el mundo físico (figura 1.3). En la teoría general de la relatividad tenemos cierto tipo de estructura que realmente subyace al comportamiento del mundo físico de una forma extraordinariamente precisa. Estas características fundamentales de nuestro mundo no suelen descubrirse observando cómo se comporta la naturaleza, aunque esto es obviamente muy importante. Uno tiene que estar preparado para desechar teorías que pudieran atraer por muchas otras razones pero que no encajan con los hechos. En esta tenemos una teoría que sí encaja con los hechos con una precisión extraordinaria. La exactitud corresponde aproximadamente a un número de cifras doble que el que se obtiene en la teoría newtoniana; en otras palabras, se sabe que la teoría general de la relatividad es correcta hasta una parte en 1014, mientras que la teoría newtoniana solo es exacta hasta una parte en 107. Esta mejora equivale al aumento que tuvo lugar entre el siglo XVII y nuestros días de la precisión con que se sabía que era correcta la teoría newtoniana. Newton sabía que su teoría era válida hasta, aproximadamente, una parte en 1.000, mientras que ahora se sabe que es exacta hasta una parte en 107.
La teoría de la relatividad general de Einstein es solo una teoría, por supuesto. ¿Qué sucede con la estructura del mundo real? Existen tres tipos de modelo estándar que se deducen de la teoría de Einstein y estos tipos están definidos por un parámetro, que es, de hecho, el denotado por k en la figura 1.16.
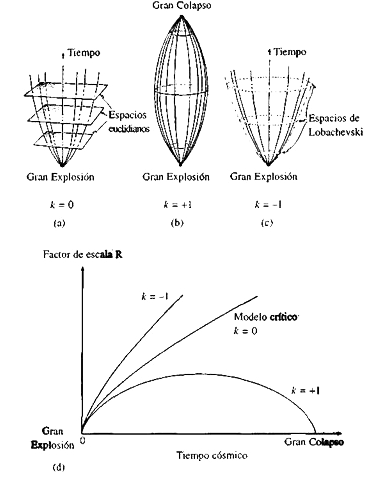
Figura 1.16.
(a) Imagen espacio-temporal de un Universo en expansión con secciones espaciales euclidianas (se muestran dos dimensiones espaciales): k = 0.
(b) Como en (a) pero para un Universo en expansión (y posterior contracción) con secciones espaciales esféricas: k = +1.
(c) Como en (a) pero para un Universo en expansión con secciones espaciales de Lobachevski: k = −1.
(d) Dinámica de los tres diferentes tipos de modelos de Friedman.
Existe otro parámetro que aparece a veces en discusiones cosmológicas y que se conoce como la constante cosmológica. Einstein consideraba que la introducción de la constante cosmológica en las ecuaciones de la relatividad general había sido el mayor error de su vida, y por eso yo también la dejaré fuera. Si nos vemos obligados a traerla de nuevo…, bien, entonces tendremos que convivir con ella.
Suponiendo que la constante cosmológica es cero, los tres tipos de Universo que están descritos por la constante k se ilustran en la figura 1.16.
En el diagrama, k toma los valores 1, 0 y −1, porque todas las demás propiedades de los modelos se han escrito en la escala conveniente. Una forma más apropiada hubiera sido hablar de la edad o la escala del Universo, y entonces tendríamos un parámetro continuo; pero, cualitativamente, los tres modelos diferentes pueden considerarse definidos por la curvatura de las secciones espaciales del Universo. Si las secciones espaciales son planas, tienen curvatura cero y k = 0 (figura 1.16.a). Si las secciones espaciales están curvadas positivamente, lo que significa que el Universo se cierra sobre sí mismo, entonces k = +1 (figura 1.16.b). En todos estos modelos, el Universo tiene un estado inicial singular, la Gran Explosión, que marca su comienzo. Pero en el caso k = +1, el Universo se expande hasta un tamaño máximo y luego se comprime de nuevo hasta un Gran Colapso. Como alternativa, existe el caso k = −1, en el que el Universo se expande para siempre (figura 1.16.c). El caso k = 0 es la frontera límite entre los casos k = 1 y k = −1. He mostrado las relaciones radio-tiempo para estos tres tipos de Universo en la figura 1.16.d. El radio puede considerarse como cierta escala típica en el Universo, y puede verse que solo en el caso k = +1 se concentra hasta un Gran Colapso, mientras que, en los otros dos, el Universo se expande indefinidamente.
Quiero considerar el caso k = −1 con algo más de detalle: es quizá el más difícil de entender de los tres. Existen dos razones para estar interesado particularmente en esta situación. Una razón es que, si se toman al pie de la letra las observaciones existentes en este momento, es el modelo preferido. Según la teoría general de la relatividad, la curvatura del espacio está determinada por la cantidad de materia presente en el Universo y no parece haber suficiente para cerrar la geometría del Universo. Ahora bien, pudiera ser que haya un montón de materia oscura y oculta que todavía no conocemos. En este caso, el Universo podría ser uno de los otros modelos; pero si no hay una gran cantidad de materia extra, mucha más de la que creemos que debe estar presente dentro de las imágenes ópticas de las galaxias, entonces el Universo tendría k = −1. La otra razón es que, ¡este es el modelo que yo prefiero! Las propiedades de las geometrías k = −1 son particularmente elegantes.
¿Qué aspecto tienen los universos k = −1? Sus secciones espaciales tienen lo que se conoce como geometría hiperbólica o de Lobachevski. Para obtener una imagen de una geometría de Lobachevski lo mejor es observar uno de los grabados de Escher. De su serie denominada Límites circulares: el Límite circular IV se muestra en la figura 1.17.

Figura 1.17. Límite circular IV de M.C. Escher © 1988 Cordon. Art-Baarn-Holland. Todos los derechos reservados. (Representación de una espacio de Lobachevski).
Esta es la descripción del Universo de Escher: ¡comprueben que está llena de ángeles y demonios! Un aspecto a señalar es que parece como si las figuras se amontonasen hacia el borde del límite circular. Esto ocurre debido a que esta representación del espacio hiperbólico está dibujada en una hoja de papel plano ordinario; en otras palabras, en el espacio euclidiano. Lo que ustedes tienen que imaginar es que todos los demonios son en realidad de la misma forma y tamaño, de modo que, si ustedes vivieran en este Universo cerca del borde del diagrama, les parecerían exactamente iguales que los que están en el centro. Esta imagen proporciona alguna idea de lo que sucede en la geometría de Lobachevski: a medida que caminan desde el centro hacia el borde, ustedes tienen que imaginar que, debido al modo en que ha tenido que distorsionarse la imagen geométrica, la geometría real allí es exactamente la misma que en el centro, de modo que la geometría que les rodea sigue siendo la misma independientemente de cómo se muevan.
Este es quizá el ejemplo más sorprendente de una geometría bien definida. Pero la geometría euclidiana es, a su manera, igual de notable. La geometría euclidiana proporciona una maravillosa ilustración de la relación entre las matemáticas y la física. Esta geometría es una parte de las matemáticas pero los griegos la consideraban también una descripción del modo de ser del mundo. En realidad, resulta ser una descripción extraordinariamente precisa de la forma real del mundo: no absolutamente exacta, porque la teoría de Einstein nos dice que el espacio-tiempo está ligeramente curvado de diversas formas, pero, en cualquier caso, es una descripción del mundo extremadamente fiel. En otro tiempo, la gente se preocupaba por saber si otras geometrías eran posibles o no.
En particular, se interesaban por lo que se conoce como quinto postulado de Euclides, que puede reformularse como el enunciado según el cual, si existe una línea recta en un plano y hay un punto exterior a esa recta, entonces existe una única paralela a dicha línea que pasa por ese mismo punto. Se pensaba que esto quizá podría demostrarse a partir de los otros axiomas más obvios de la geometría euclidiana; pero resulta que no es posible, y de ello surgió la noción de geometría no euclidiana.
En las geometrías no euclidianas, los ángulos de un triángulo no suman 180°. Este es otro ejemplo en el que uno piensa que las cosas van a hacerse más complicadas porque, en la geometría euclidiana, los ángulos de un triángulo sí suman 180° (figura 1.18.a). Pero luego se ve que, en la geometría no euclidiana, si se toma la suma de los ángulos de un triángulo y se resta de 180°, esta diferencia es proporcional al área del triángulo.
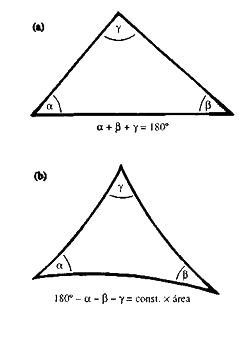
Figura 1.18.
(a) Un triángulo en el espacio euclidiano.
(b) Un triángulo en el espacio de Lobachevski.
En la geometría euclidiana, el área de un triángulo es algo complicada de escribir en términos de ángulos y longitudes. En la geometría no euclidiana de Lobachevski existe esta fórmula maravillosamente simple, debida a Lambert, que hace posible calcular el área del triángulo (figura 1.18.b). De hecho, Lambert obtuvo su fórmula antes de que se descubriera la geometría no euclidiana, ¡y esto es algo que nunca he acabado de entender!
Hay aquí otro punto muy importante que se refiere a los números reales. Estos son absolutamente fundamentales para la geometría euclidiana. Fueron introducidos esencialmente por Eudoxo en el siglo IV a. de C. y aún están con nosotros. Son los números que describen toda nuestra física. Como veremos más adelante, los números complejos también son necesarios, pero están basados en los números reales.
Examinemos otro de los grabados de Escher para ver cómo funciona la geometría de Lobachevski.
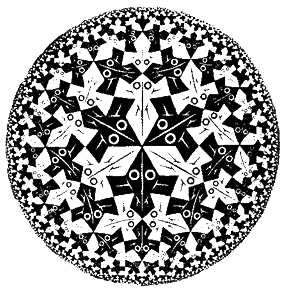
Figura 1.19. Límite circular I de M.C. Escher © 1988 Cordon. Art-Baarn-Holland. Todos los derechos reservados.
La figura 1.19 es incluso más bonita que la figura 1.17 para entender esta geometría, porque las líneas rectas son más obvias, están representadas por arcos de círculo que cortan los límites en ángulos rectos. Por ello, si ustedes fueran personas lobachevskianas y vivieran en esta geometría, lo que ustedes considerarían una línea recta sería uno de estos arcos. Podemos verlas claramente en la figura 1.19: algunas son líneas rectas euclidianas que pasan por el centro del diagrama pero todas las demás son arcos curvos. Algunas de estas líneas rectas se muestran en la figura 1.20.
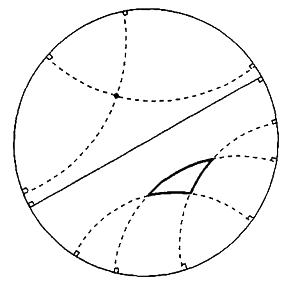
Figura 1.20. Aspectos de la geometría de un espacio de Lobachevski (hiperbólico) como el ilustrado por Límite circular I.
En este diagrama he marcado un punto que no se encuentra en la línea recta (diámetro) que cruza el diagrama. La población lobachevskiana puede trazar dos (y más) líneas independientes paralelas al diámetro que pasan por dicho punto, tal como he indicado. Así pues, el postulado de las paralelas se viola en esta geometría. Además, ustedes pueden dibujar triángulos y calcular la suma de los ángulos de los triángulos para calcular sus áreas. Esto puede darles alguna idea de la naturaleza de la geometría hiperbólica.
Déjenme poner otro ejemplo. Dije que yo prefiero la geometría hiperbólica lobachevskiana. Una de las razones es que su grupo de simetrías es exactamente el mismo que el que ya hemos encontrado, a saber, el grupo de Lorentz, el grupo de la relatividad especial, o el grupo de simetría de los conos de luz de la relatividad. Para ver qué es esto, he dibujado un cono de luz en la figura 1.21 pero con algunas piezas extra. He tenido que suprimir una de las dimensiones espaciales para representarlo en el espacio tridimensional.
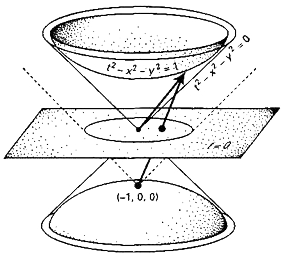
Figura 1.21. Espacio de Lobachevski insertado como una rama hiperboloide en el espacio-tiempo de Minkowski. La proyección estereográfica le hace corresponder el disco de Poincaré, cuya frontera es el círculo dibujado en el plano t = 0.
El cono de luz está descrito por la ecuación usual mostrada en el diagrama:
t2 − x2 − y2 = 0.
Las superficies en forma de cuenco que se muestran arriba y abajo están situadas a una distancia unidad del origen en esta geometría minkowskiana. (Distancia en la geometría minkowskiana es realmente tiempo, el tiempo propio que es medido físicamente por relojes en movimiento). Así pues, estas superficies representan la superficie de una esfera para la geometría minkowskiana. Resulta que la geometría intrínseca de la esfera es realmente una geometría lobachevskiana (hiperbólica). Si consideramos una esfera ordinaria en el espacio euclidiano, podemos girarla y el grupo de simetrías es el grupo de rotaciones de la esfera. En la geometría de la figura 1.21, el grupo de simetrías es el asociado con la superficie mostrada en el diagrama; en otras palabras, con el grupo de Lorentz de rotaciones. Este grupo de simetrías describe cómo se transforman el espacio y el tiempo cuando se mantiene fijo un punto concreto en el espacio-tiempo: rotando el espacio-tiempo de diferentes maneras. Vemos ahora, con esta representación, que el grupo de simetrías del espacio lobachevskiano es esencialmente idéntico al grupo de Lorentz.
La figura 1.21 ilustra una versión minkowskiana de la proyección estereográfica mostrada en la figura 1.10.c. El equivalente al polo sur es ahora el punto (−1, 0, 0), y proyectamos puntos de la superficie superior en forma de cuenco en la superficie plana en t = 0, que es la análoga al plano ecuatorial en la figura 1.10.c. Mediante este procedimiento, proyectamos todos los puntos de la superficie superior en el plano t = 0. Todos los puntos proyectados están dentro de un disco en el plano t = 0, que se suele denominar disco de Poincaré. Así es precisamente como surgen los diagramas del límite circular de Escher: la superficie hiperbólica (lobachevskiana) ha sido aplicada en el disco de Poincaré. Además, esta aplicación se comporta del mismo modo que la proyección de la figura 1.10.c: conserva ángulos y círculos, y todo resulta geométricamente de una forma muy bella. Bien, quizá me he dejado llevar por mi entusiasmo, ¡me temo que esto es lo que les pasa a los matemáticos cuando se encariñan con algo!
El punto intrigante es que, cuando uno se deja llevar por un tema como la geometría del problema anterior, el análisis y los resultados tienen una brillantez que los sostiene, mientras que los análisis que no poseen esta elegancia matemática se quedan en nada. Hay algo particularmente elegante en la geometría hiperbólica. Sería muy bonito, al menos para las personas como yo, que el Universo estuviese construido también de este modo. Déjenme decir que tengo otras razones para creer que esto es así. A muchas otras personas no les gustan estos universos hiperbólicos abiertos: frecuentemente, prefieren universos cerrados, tales como los ilustrados en la figura 1.16.b, que son bonitos y confortables. Está bien; los universos cerrados siguen siendo muy grandes. Por otro lado, a muchos otros les gustan los modelos planos (figura 1.16.a) porque existe un cierto tipo de teoría del Universo primitivo, la teoría inflacionaria, que sugiere que la geometría del Universo tendría que ser plana. Debería decir que yo no creo en estas teorías.
Los tres tipos estándar de modelo del Universo se conocen como modelos de Friedman y se caracterizan porque son muy, muy simétricos. Son inicialmente modelos en expansión, pero en todo instante el Universo es perfectamente uniforme en todas partes. Esta hipótesis está incorporada en la estructura de los modelos de Friedman y se conoce como principio cosmológico. Dondequiera que uno esté, el universo de Friedman tiene la misma apariencia en todas direcciones. Resulta que nuestro Universo actual es así hasta un grado notable. Si las ecuaciones de Einstein son correctas, y yo he mostrado que la teoría concuerda con la observación hasta un grado extraordinario, entonces nos vemos obligados a tomar en serio los modelos de Friedman. Todos estos modelos tienen este rasgo molesto, conocido como la Gran Explosión, donde todo falla, exactamente, en el comienzo. El Universo es infinitamente denso, infinitamente caliente y así sucesivamente; algo ha ido fallando en la teoría. De todas maneras, si se acepta que esta fase muy caliente y muy densa tuvo lugar realmente, podemos hacer predicciones sobre cuál debería ser hoy el contenido térmico del Universo y una de estas afirma que, en el momento actual, dicho contenido debería consistir en un fondo uniforme de radiación de cuerpo negro a nuestro alrededor. Precisamente este tipo de radiación fue descubierto por Penzias y Wilson en 1965. Las observaciones más recientes del espectro de esta radiación, que se conoce como radiación de fondo cósmico de microondas, hechas por el satélite COBE, muestran que tiene un espectro de cuerpo negro con extraordinaria precisión (figura 1.22).
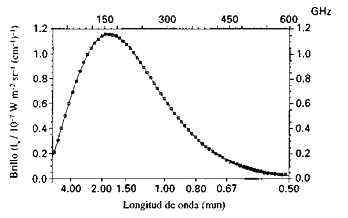
Figura 1.22. Acuerdo exacto entre las medidas de COBE del espectro de la radiación de fondo cósmico de microondas y la naturaleza térmica esperada de la radiación de la Gran Explosión (línea continua).
Todos los cosmólogos interpretan la existencia de esta radiación como evidencia de que nuestro Universo pasó por una fase densa y caliente. Esta radiación nos está diciendo, por consiguiente, algo sobre la naturaleza del Universo primitivo; no nos está diciendo todo, sino que algo parecido a la Gran Explosión tuvo lugar. En otras palabras, el Universo debe de haber sido muy parecido a los modelos ilustrados en la figura 1.16.
Hay otro descubrimiento muy importante hecho por el satélite COBE, y es que, aunque la radiación de fondo cósmico de microondas es notablemente uniforme y todas sus propiedades pueden ser explicadas de forma matemáticamente muy bella, el Universo no es en absoluto uniforme. Existen minúsculas pero reales irregularidades en la distribución de la radiación en el cielo. De hecho, esperábamos que estas minúsculas irregularidades estuvieran presentes en el Universo primitivo: al fin y al cabo, nosotros estamos aquí para observar el Universo y, ciertamente, no somos solo una mancha uniforme. El Universo es probablemente más parecido a las imágenes ilustradas en la figura 1.23. Para mostrar mi imparcialidad, estoy utilizando como ejemplos tanto un universo abierto como uno cerrado.
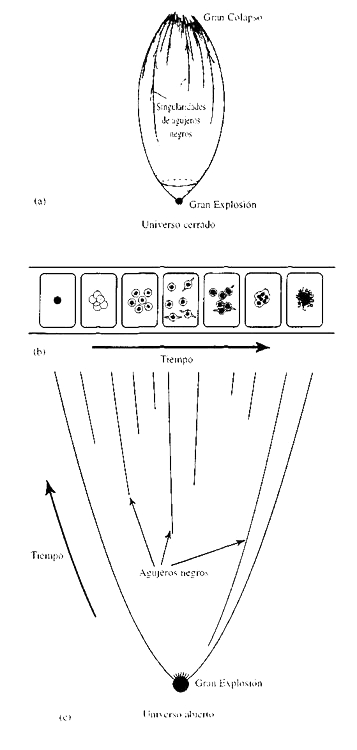
Figura 1.23.
(a) Evolución de un modelo cerrado del mundo con la formación de agujeros negros, a medida que objetos de diferentes tamaños alcanzan los puntos finales de su evolución. Puede preciarse que se espera que haya un horrible caos en el Gran Colapso.
(b) Película de la secuencia de sucesos ocurridos en (a).
(c) Evolución de un modelo abierto que muestra la formación de agujeros negros en diferentes instantes.
En el Universo cerrado, las irregularidades se desarrollarán para formar estructuras observables reales —estrellas, galaxias y demás— y, al cabo de un tiempo, aparecerán agujeros negros a partir del colapso de estrellas, mediante la acumulación de masa en los centros de las galaxias y así sucesivamente. Todos estos agujeros negros tienen centros singulares, muy parecidos a una Gran Explosión invertida. Sin embargo, no es tan simple como eso. Según la imagen que hemos desarrollado, la Gran Explosión inicial es un estado bonito, simétrico y uniforme, pero el punto final del modelo cerrado es un caos horrible, en el que todos los agujeros negros llegan eventualmente a juntarse para producir una increíble confusión en el Gran Colapso final (figura 1.23.a). La evolución de este modelo cerrado está ilustrada esquemáticamente en las secuencias mostradas en la figura 1.23.b. En el caso de un modelo de universo abierto, los agujeros negros siguen formándose: sigue habiendo una singularidad inicial y aparecen singularidades en los centros de los agujeros negros (figura 1.23.c).
Resalto estas características de los modelos de Friedman para mostrar que hay una gran diferencia entre lo que parece que vemos en el estado inicial y lo que esperamos encontrar en el futuro remoto. Este problema está relacionado con una ley fundamental de la física conocida como segunda ley de la termodinámica.
Podemos entender la segunda ley de la termodinámica mediante un ejemplo sencillo de la vida cotidiana. Imaginemos un vaso de vino situado en el borde de una mesa: podría caer de la mesa, romperse en pedazos y quedar el vino salpicado sobre la alfombra (figura 1.24).
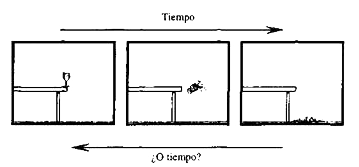
Figura 1.24. Las leyes de la mecánica son reversibles con respecto al tiempo; pese a todo, la ordenación temporal de una escena desde el fotograma derecho al izquierdo es algo que nunca se experimenta, mientras que desde el fotograma izquierdo al derecho resulta perfectamente normal.
No hay nada en la física newtoniana que nos diga que no puede suceder el proceso inverso. Sin embargo, esto no se observa nunca: nunca vemos vasos de vino que se recomponen por sí solos y que el vino sea extraído de la alfombra y entre en el vaso recompuesto. Por lo que concierne a las leyes detalladas de la física, un sentido del tiempo es exactamente tan bueno como el otro. Para entender esta diferencia necesitamos la segunda ley de la termodinámica, que nos dice que la entropía del sistema aumenta con el tiempo. Esta magnitud, llamada entropía, es menor cuando el vaso está sobre la mesa que cuando está hecho pedazos en el suelo. De acuerdo con la segunda ley de la termodinámica, la entropía del sistema ha aumentado. Hablando en términos muy generales, la entropía es una medida del desorden de un sistema. Para expresar este concepto de forma más precisa tenemos que introducir el concepto de espacio de fases.
Un espacio de fases es un espacio de un enorme número de dimensiones, y cada punto de este espacio multidimensional describe las posiciones y los momentos de todas las partículas que constituyen el sistema bajo consideración. En la figura 1.25 hemos seleccionado un punto concreto en este enorme espacio de fases, un punto que representa dónde están situadas todas las partículas y cómo se están moviendo. Conforme evoluciona el sistema de partículas, el punto se desplaza hacia algún otro lugar en el espacio de fases y yo lo he mostrado serpenteando de un lugar a otro en este espacio.
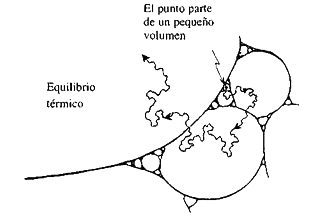
Figura 1.25. La segunda ley de la termodinámica en acción: a medida que el tiempo evoluciona, el punto en el espacio de fases entra en compartimentos de volumen cada vez mayor. En consecuencia, la entropía aumenta continuamente.
Esta línea serpenteante representa la evolución ordinaria del sistema de partículas. Aún no hay entropía allí. Para tener entropía tenemos que dibujar pequeñas burbujas alrededor de regiones en donde amontonamos aquellos estados diferentes que uno no puede distinguir. Esto puede parecer algo confuso: ¿qué es lo que se entiende por no puede distinguir? ¿Depende de quién está mirando y con qué cuidado mira?
Bien, una de las cuestiones algo delicadas de la física teórica consiste en decir exactamente lo que se entiende por entropía. Esencialmente, lo que se quiere decir es que uno tiene que agrupar estados de acuerdo con lo que se conoce como granulado grueso, es decir, de acuerdo con aquellas cosas que uno no puede distinguir. Uno toma todos los estados que, digamos, yacen en esta región del espacio de fases, los amontona, considera el volumen de dicha región del espacio de fases, toma el logaritmo del volumen y lo multiplica por la constante conocida como constante de Boltzmann, y eso es la entropía. Lo que nos dice la segunda ley de la termodinámica es que la entropía aumenta, realmente algo bastante estúpido: todo consiste en que, si el sistema empieza en una caja minúscula y se le permite evolucionar, se acomodará a cajas cada vez más grandes. Es muy probable que esto suceda porque, si uno considera el problema cuidadosamente, las cajas más grandes son extraordinariamente más grandes que las cajas pequeñas vecinas. Por ello, si uno se encuentra en una de las cajas grandes, no hay prácticamente ninguna posibilidad de que vuelva a una caja más pequeña. Eso es todo lo que hay. El sistema simplemente vaga por el espacio de fases en cajas cada vez mayores. Esto es lo que nos afirma la segunda ley. ¿O no es así?
En realidad, esta es solo la mitad de la explicación. La ley nos dice que, si conocemos el estado del sistema ahora, podemos prever su estado más probable en el futuro. Pero nos dará una respuesta completamente errónea si tratamos de utilizar el mismo argumento hacia atrás. Supongamos que el vaso está en el borde de la mesa. Podemos preguntar: ¿Cuál es la forma más probable en la que pudo haber llegado allí? Si ustedes utilizan el argumento que acabamos de presentar hacia atrás, concluirán que lo más probable es que empezara como un gran amasijo en la alfombra y que luego saltó por sí solo desde la alfombra y se recompuso en la mesa. Evidentemente no es esta la explicación correcta: la explicación correcta es que alguien lo puso allí. Y dicha persona lo puso allí por alguna razón, que a su vez era debida a alguna otra razón y así sucesivamente. La cadena de razonamiento se remonta cada vez más atrás hasta estados cada vez menores de entropía en el pasado. La curva física correcta es la real ilustrada en la figura 1.26 (no la retrodicha): la entropía disminuye, y disminuye, y disminuye en el pasado.
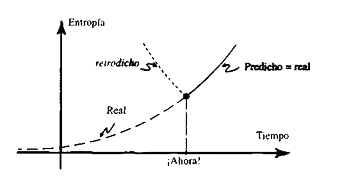
Figura 1.26. Si utilizamos el argumento representado en la figura 1.25 en el sentido contrario del tiempo retrodecimos que la entropía también debería aumentar en el pasado, a partir de su valor actual. Esto está en franca contradicción con la observación.
La razón de que la entropía aumente en el futuro se explica por la acomodación a cajas cada vez mayores; la razón de que se reduzca en el pasado es algo completamente diferente. Debe de haber habido algo que la hizo disminuir en el pasado. ¿Qué pudo ser? A medida que retrocedemos en el tiempo, la entropía se hace cada vez más pequeña hasta que, finalmente, terminamos en la Gran Explosión.
Debe de haber habido algo muy, muy especial en la Gran Explosión, pero qué fue exactamente es una cuestión controvertida. Una teoría popular, en la que dije que no creía pero con la que simpatiza mucha gente, es la idea del universo inflacionario. Esta idea consiste en que el Universo es tan uniforme a gran escala debido a algo que se supone que ha tenido lugar en las fases muy tempranas de su expansión. Se supone que una tremenda expansión tuvo lugar cuando el Universo tenía solo unos 10−36 segundos y la idea es que, independientemente del aspecto que tuviera en aquellas etapas muy tempranas, si se expande en un factor enorme de aproximadamente 1060, entonces, parecerá plano. De hecho, esta es una razón que justifica la popularidad del Universo plano.
Pero, tal como está, el argumento no hace lo que se le supone: lo que cabría esperar en este estado inicial, si fuera escogido al azar, sería una horrible mescolanza y, si se expande esta mescolanza en este factor enorme, sigue siendo una completa mescolanza. De hecho, parece cada vez peor cuanto más se expande (figura 1.27).
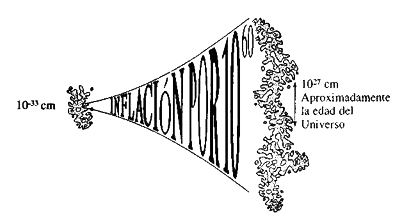
Figura 1.27. Ilustración del problema de la inflación de irregularidades genéricas en el Universo primitivo.
Por eso, el argumento por sí mismo no explica por qué el Universo es tan uniforme. Necesitamos una teoría que describa cómo fue realmente la Gran Explosión. No sabemos cuál es esta teoría pero sabemos que tiene que involucrar una combinación de física a gran escala y a pequeña escala. Tiene que involucrar tanto la física cuántica como la física clásica. Además, afirmaré que entre las implicaciones de la teoría debe estar que la Gran Explosión era tan uniforme como observamos que lo es ahora. Quizá semejante teoría termine produciendo un universo hiperbólico de Lobachevski, como la imagen que yo prefiero, pero no insistiré en ello.
Volvamos de nuevo a las imágenes de los universos cerrado y abierto (figura 1.28). Ahora he incluido una imagen de la formación de un agujero negro, que será bien conocida para los expertos. La materia que se colapsa en un agujero negro produce una singularidad, y eso es lo que representan las líneas oscuras en los diagramas espacio-temporales del Universo.
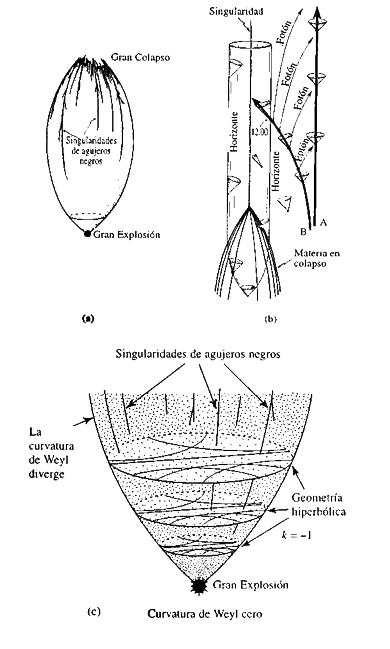
Figura 1.28.
(a) La historia entera de un Universo cerrado que empieza con una Gran Explosión uniforme de baja entropía con Weyl = 0 y termina con un Gran Colapso de alta entropía —que representa la coalescencia de muchos agujeros negros— con Weyl → ∞.
(b) Agujero negro.
(c) La historia de un Universo abierto, empezando de nuevo en una Gran Explosión uniforme de baja entropía con Weyl = 0.
Quiero introducir una hipótesis que yo llamo la hipótesis de curvatura de Weyl. Esto no es una consecuencia de ninguna teoría conocida. Como he dicho, no sabemos cuál es la teoría, porque no sabemos cómo combinar la física de lo muy grande y de lo muy pequeño. Cuando descubramos dicha teoría, una de sus consecuencias debería ser esta característica que yo he llamado hipótesis de curvatura de Weyl. Recordemos que la curvatura de Weyl es esa pequeña parte del tensor de Riemann que provoca distorsiones y efectos de marea. Por alguna razón que todavía no entendemos, en las inmediaciones de la Gran Explosión, la combinación apropiada de teorías debe dar como resultado que el tensor de Weyl sea esencialmente cero, o más bien que esté limitado por un valor muy pequeño. Esto nos daría un Universo como el que se muestra en la figura 1.28.a o 1.28.c, y no como el de la figura 1.29.
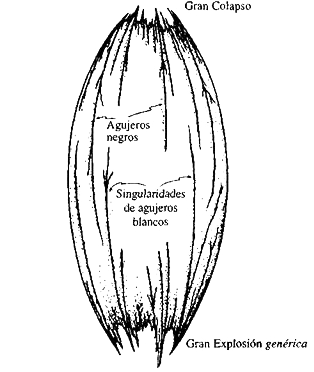
Figura 1.29. Si se elimina la ligadura Weyl = 0, entonces tenemos también una Gran Explosión con alta entropía, con Weyl → ∞. Un universo semejante estaría plagado de agujeros blancos, y no habría segunda ley de la termodinámica, lo que está en franca contradicción con la experiencia.
La hipótesis de curvatura de Weyl tiene asimetría temporal y se aplica solo a las singularidades de tipo pasado y no a las singularidades futuras. Si la misma flexibilidad de permitir que el tensor de Weyl sea general, que he aplicado al futuro, se aplicara también al pasado del Universo en el modelo cerrado, terminaríamos con un Universo de apariencia horrible, con tanta mezcla en el pasado como en el futuro (figura 1.29). Esto no se parece nada al Universo en que vivimos.
¿Cuál es la probabilidad de que, puramente por azar, el Universo tuviera una singularidad inicial que se pareciera siquiera remotamente a esto? La probabilidad es menor que una parte en 1010123. ¿De dónde procede esta estimación? Se deriva de una fórmula de Jacob Beckenstein y Stephen Hawking relativa a la entropía de los agujeros negros y, si se aplica en este contexto particular, se obtienen numerosas respuestas. Depende de lo grande que sea el Universo pero, si se adopta mi Universo favorito, el número es, de hecho, infinito.
¿Qué dice esto sobre la precisión que debe estar implicada en la puesta en marcha de la Gran Explosión? Es realmente muy, muy extraordinaria. He ilustrado la probabilidad en un dibujo del Creador, que apunta con una aguja minúscula al punto del espacio de fases que representa las condiciones iniciales a partir de las que debe haber evolucionado nuestro Universo si tiene que parecerse remotamente al Universo en que vivimos (figura 1.30).

Figura 1.30. Para producir un universo parecido al Universo en que vivimos, el Creador tendría que apuntar a un volumen absurdamente minúsculo del espacio de fases de universos posibles: como mucho a 1/1010123 del Universo entero. (¡La aguja y el punto señalado no están dibujados a escala!).
Para apuntar, el Creador tiene que localizar dicha punta en el espacio de fases con una precisión de una parte en 1010123. Si yo pusiera un cero en cada partícula elemental del Universo, seguiría sin poder escribir todo el número. Es un número inimaginable.
He estado hablando de precisión, de cómo encajan las matemáticas y la física con precisión extraordinaria. He hablado también sobre la segunda ley de la termodinámica, que a menudo se considera como una ley bastante difusa —se refiere a aleatoriedad y a azar— y, pese a todo, hay algo muy preciso oculto bajo esta ley. Tal como se aplica al Universo, tiene que ver con la precisión con la que fue fijado el estado inicial. Esta precisión debe de tener algo que ver con la unión de la teoría cuántica y la relatividad general, una teoría que no tenemos. En el próximo capítulo, sin embargo, diré algo sobre el tipo de cosas que deberían estar implicadas en una teoría semejante.