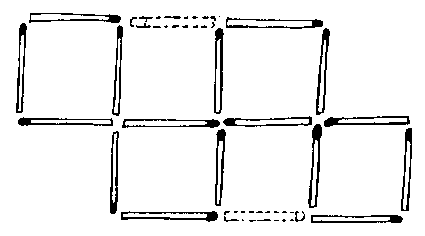
Facilita mucho la resolución de este «clásico» de los rompecabezas con cerillas (que, curiosamente, poca gente logra resolver) el caer en la cuenta de que hay 16 cerillas (casi nadie se molesta en contarlas, y son demasiadas para captar su número a golpe de vista), lo que significa que, al igual que en el problema 8, los cuatro cuadrados no pueden tener ningún lado común, puesto que entonces sobrarían tantas cerillas como lados hubiera compartidos por dos cuadrados adyacentes; por lo tanto, los cuatro cuadrados sólo se pueden tocar por los vértices, como en la figura.

Moraleja: Cuenta las cerillas antes de usarlas.