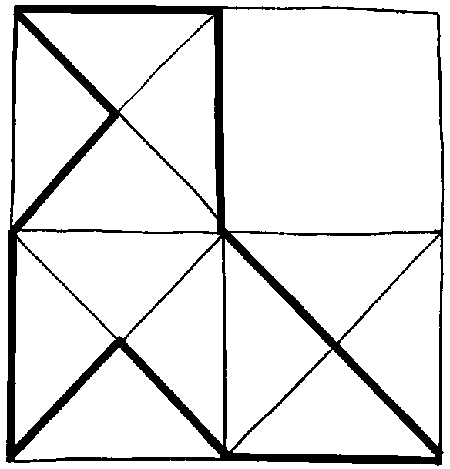
Por cada uno de los segmentos que confluyen en un vértice del sobre, el lápiz puede «llegar» a ese punto o «marcharse» de él. Como hay dos vértices en los que confluyen tres segmentos (el 4 y el 5), uno de ellos tiene que ser el punto inicial del recorrido del lápiz y el otro el punto final, puesto que si el punto inicial fuera otro cualquiera, el lápiz tendría que llegar-salir-llegar tanto al punto 4 como al 5, es decir, tendría que haber dos puntos finales del recorrido (pues una vez el lápiz ha llegado al punto 3 o al 4 por segunda vez ya no le quedan caminos por donde volver a salir), lo cual es imposible.
Una vez establecido esto, no es difícil dibujar el sobre de un solo trazo según distintos recorridos, por ejemplo, 4-5-2-3-1-2-4-3-5 ó 4-3-5-4-2-3-1-2-5.

Moraleja: No pierdas el tiempo intentando resolver por tanteo lo que puede someterse al implacable escrutinio de la lógica.