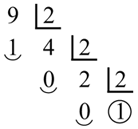
Con lo aprendido hasta ahora y unos minutos de práctica tienes más que suficiente para dominar las variantes más usuales del nim; pero si quieres ser infalible en cualquiera de sus modalidades concebibles tendrás que convertirte en un pequeño ordenador, es decir, tendrás que operar con números binarios.
¿Qué son los números binarios? Bien, un ingenioso de la era de la informática no puede ignorar este tema, así que, aunque no te interese especialmente lograr el dominio absoluto del nim, harás bien en enterarte.
Decimos que utilizamos el sistema de numeración decimal porque en los números, tal como los escribimos habitualmente, las cifras representan potencias sucesivas de 10, en sentido creciente de derecha a izquierda. Así, 532 significa que tenemos 2 unidades, 3 decenas y 5 centenas (decenas de decenas); expresado de forma más matemática: 532 = 5 x 102 + 3 x 10 + 2.
Para expresar los números en sistema decimal (o, lo que es lo mismo, «en base diez») nos basta con diez cifras, que representan los números del uno al nueve más el cero, puesto que al llegar al diez lo expresamos como una unidad de segundo orden (una decena); por eso lo escribimos así, 10: la cifra de la derecha (0) indica que no hay ninguna unidad «suelta», mientras que la segunda cifra a partir de la derecha (1) indica que tenemos una unidad de segundo orden, es decir, una decena (puesto que la base es diez). Si la base fuese cinco en lugar de diez (cosa que probablemente habría ocurrido de tener los hombres una sola mano en vez de dos), el número 13, por ejemplo, significaría que tenemos 3 unidades y 1 «cinquena», es decir, equivaldría a ocho (y a lo mejor dejaría de ser un número aciago).
En base dos sólo son necesarias dos cifras, el 1 y el 0; 2 en base 2, naturalmente, es 10 (1 pareja y O unidades); tres es 11 (1 pareja y 1 unidad); cuatro es 100 (1 pareja de parejas, O parejas y O unidades); cinco es 101, etc.
Para pasar un número cualquiera a la base dos, o, lo que es lo mismo, al sistema binario hay que descomponerlo en potencias de 2, lo cual es más fácil de hacer que de explicar. Por ejemplo, 9 =23+ 1 (23=2 x 2 x 2 = 8), luego 9 en binario será 1001 (los dos ceros intermedios indican que no hay ningún 22 ni ningún 2, es decir, ninguna pareja ni pareja de parejas: sólo una unidad y una «pareja de parejas de parejas»). En la práctica lo haríamos así:
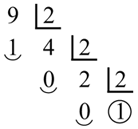
El último cociente es la primera cifra de la izquierda, a la que siguen los restos de las sucesivas divisiones en orden inverso. Otro ejemplo:
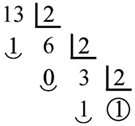
Trece en base dos en 1101 (23+22+ 1=8+ +4+ 1).
¿Por qué usan los ordenadores el sistema binario en vez del decimal, que es mucho más compacto (un número grande, en base dos, requiere un montón de ceros y unos)? Muy sencillo: porque en vez de dedos tienen conmutadores electrónicos, susceptibles de hallarse en dos estados distintos (como el interruptor de una lámpara, que puede estar encendida o apagada). Haciendo corresponder el 0 a uno de los estados y el 1 al otro y combinando entre sí miles de conmutadores se puede realizar, en sistema binario, todo tipo de operaciones a las velocidades vertiginosas de los impulsos eléctricos. Para nuestra mayor comodidad, luego los ordenadores traducen los resultados en números decimales (o en palabras), pero todo su «discurso interior» se desarrolla en el sistema binario; lo que en la jerga de la informática se denomina el «lenguaje máquina» se basa en un alfabeto elemental de sólo dos signos.
Este preámbulo no era imprescindible para jugar al nim, pero sí para manejarse en el mundo moderno.
Volviendo al juego: la estrategia binaria para ganar siempre al nim, en cualquiera de sus variantes, es la siguiente: escribimos en base dos el número de fichas de cada fila, los disponemos uno sobre otro como para hacer una suma y sumamos cada columna. Por ejemplo, en el caso del nim tradicional, de tres filas de 5, 4 y 3 fichas, tendríamos:
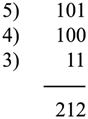
Pues bien, si todas las columnas suman números pares o ceros estamos ante una situación perdedora; si alguna de las columnas da una suma impar, la situación no es perdedora, luego es ganadora, pues haciendo una jugada adecuada podemos convertirla en perdedora para el otro jugador. En el caso que nos ocupa vemos que la columna del centro suma 1, luego la situación es ganadora para el que le toca jugar, cosa que ya sabíamos por el análisis anterior, pues hemos visto que quitando dos fichas de la fila de tres se tiene la victoria asegurada.
Comprobémoslo por el sistema binario: quitando dos fichas de la fila de tres queda la formación 5-4-1, que en base dos da:
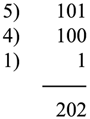
Todas las sumas de las columnas dan par o cero, luego la situación es perdedora para el que tiene que jugar ahora, cosa que ya sabíamos. Por cierto, si el paciente lector se molesta en comprobarlo, verá que la única forma de convertir la situación inicial 5-4-3 en perdedora es pasar a 5-4-1, pues es la única que no da ninguna suma impar al aplicarle la prueba binaria.