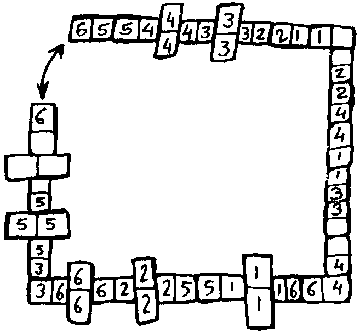
Cualquier jugador de dominó sabe que con las 28 fichas se puede formar una (mejor dicho, muchas distintas) cadena ininterrumpida siguiendo las reglas del juego. Lo que pocos saben es que cualquiera de estas cadenas se puede cerrar sobre sí misma como la de la figura, lo que equivale a decir que todas las cadenas posibles tienen el mismo número en sus dos extremos.
No, desconfiado lector, no intentes construir todas las cadenas posibles para comprobar si mi afirmación es cierta: suponiendo que pudieras hacer una por minuto, tardarías unos quince millones de años en completar tu inútil tarea, pues hay casi ocho billones de combinaciones posibles (exactamente, 7 959 229 931 520). Y digo que la tarea sería inútil, amén de fatigosa, porque, sin necesidad de llevar a cabo una comprobación exhaustiva, se puede demostrar la cerrabilidad de todas las cadenas por la vía lógica.
Para facilitar la comprensión del asunto, quitemos primero todas las dobles, con lo que nos quedarán 21 fichas en las que cada número se repite 6 veces y en 6 fichas distintas. Como es una cantidad par, y los números iguales se agrupan por parejas, sea cual sea el número que en un momento dado de la construcción de la cadena aparezca en el extremo, habrá otra ficha que lo contenga, y la cadena podrá continuar hasta que se acaben las fichas. Y como la cadena se forma adosando dos a dos números iguales y cada número se repite las mismas veces, en ambos extremos de la cadena tiene que haber el mismo número.
¿Aún no lo ves claro, obtuso lector? Bien, supongamos que en los extremos de la cadena hay números distintos, por ejemplo un 5 y un 3. Todos los cincos del interior de la cadena van por parejas (ya que la cadena se forma precisamente adosando números iguales), luego dentro de la cadena hay un número par de cincos… más uno que tenemos en el extremo, nos da un número total de cincos impar (y lo mismo pasa con los treses);> pero como sabemos que cada número se repite seis veces, esto es imposible, luego en los extremos de la cadena no puede haber números distintos;> por lo tanto, tiene que haber números iguales que, a modo de broche, permitan cerrar la cadena adosándolos entre sí. (Las fichas dobles que hemos quitado al principio para simplificar las podemos insertar, una vez formada la cadena, entre cualquier par de fichas que contengan el mismo número).
