EJERCICIO 14

Una demostración de que 90 grados equivalen a 89 grados:

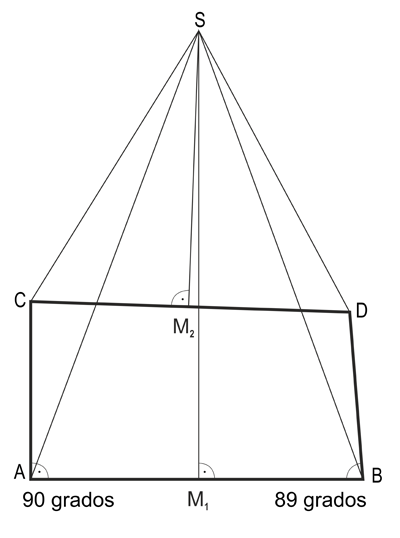
En un tramo AB se traza a la izquierda un tramo AC perpendicular al primero y a la derecha un tramo BD de la misma longitud, pero con un ángulo de 89 grados con respecto a AB. Así obtenemos el rectángulo un poco «oblicuo» ABCD.

Ahora trazamos la mediatriz sobre AB y CD, es decir, la línea perpendicular que pasa por el punto central de cada tramo. Dado que AB y CD no son paralelas, estas mediatrices tampoco son paralelas entre sí, sino que se cruzan en algún punto que llamaremos S.

Ahora unimos el punto S con A, B, C y D, tal como vemos en el dibujo (que no está hecho a escala) y examinamos las congruencias:

1. AS = BS, pues S se halla en la mediatriz de AB.
2. CS = DS, pues S se halla en la mediatriz de CD.
3. Por tanto, el triángulo ASC es congruente con BSD, pues ambos tienen iguales los tres lados (AC era por definición igual a BD).
4. Por consiguiente, el ángulo CAS es igual al ángulo DBS. Además, el ángulo SAM₁ es igual al ángulo SBM₁, pues S se halla en la mediatriz de AB.

En resumen, tenemos que:

90° = CAS + SAM₁ = DBS + SBM₁ = 89°

¿Dónde está el error?

Solución »»