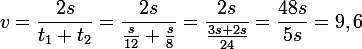Soluciones

[Solución ejercicio 1]

Si cuatro personas ocupan un metro cuadrado, cada una dispone de un área de 50 por 50 centímetros, lo que todavía se puede soportar. Aplicado a la superficie del lago de Costanza, en él cabrían 2.100 millones de personas, es decir, ¡un tercio de la humanidad!

<<

[Solución ejercicio 2]

A partir de 23 personas la probabilidad de que dos cumplan años el mismo día es superior al 50%.

El truco consiste en calcular la probabilidad de que todos los cumpleaños caigan en fechas distintas. Entre dos personas, la probabilidad de que B cumpla años en un día distinto que A es de ³⁶⁴/₃₆₅. Si se añade una persona, entonces C cumplirá años en una fecha distinta que A y B en 363 de 365 casos. Y así sucesivamente… De modo que multiplicamos

hasta que el resultado sea inferior a ¹/₂. Esto ocurre cuando hay 23 personas. A partir de este número, la probabilidad de que todos los cumpleaños caigan en un día distinto es inferior al 50%, lo que significa que hay una probabilidad de más del 50% de que dos personas cumplan años el mismo día.

<<

[Solución problema capítulo 3]

Las 10 máquinas terminan la tarea en 9 minutos

<<

[Solución ejercicio 3]

Hay exactamente tanta agua en el whisky como whisky en el agua.

La solución se puede calcular mediante la regla de tres, pero también se puede hallar por deducción lógica. Después de la operación hay la misma cantidad de líquido en ambos vasos, de modo que tiene que haber exactamente tanta agua en el whisky como whisky en el agua.

<<

[Solución ejercicio 4]

La velocidad media no es la media aritmética de las dos velocidades (10 km/h), sino

(Esta es la llamada media armónica de las dos velocidades).

Aclaración: si el trayecto a A a B mide s kilómetros, el corredor recorre la distancia, en la ida (a 12 km/h), conforme a la ecuación t = s / v , en el tiempo

En la vuelta la recorre (a 8 km/h) en más tiempo, a saber

La velocidad media se calcula dividiendo la distancia total entre el tiempo total, es decir,

<<

[Solución ejercicio 5]

Se dan 420 besos y 315 veces se aprietan las manos. (Ojo: suponemos que las parejas se van a casa juntas y por tanto los que las forman no se despiden entre sí).

<<

[Solución ejercicio 6]

Ninguno tiene razón. Los tres argumentos pueden ser plausibles y no existe ningún método «justo» para determinar quién ha ganado una elección de este tipo.

<<

[Solución ejercicio 7]

Si en el 55 % de los hogares solo vive una persona, en el 45 % restante viven por lo menos dos. Si fueran exactamente dos personas, entonces en 100 hogares habitarían en total 145 personas (55 + 2 · 45) y la proporción de personas que viven solas sería de alrededor del 38 %. En realidad es todavía más reducida, pues existen hogares en que viven más de dos personas.

<<

[Solución ejercicio 8]

La probabilidad de que al menos uno reciba el abrigo que le pertenece es del 63,3%.

El número de posibles entregas de n abrigos es n! («n factorial», es decir, el producto de 1 · 2 · 3 · … · n). La pregunta es: ¿en cuántas de estas llamadas permutaciones existe como mínimo un «punto fijo», es decir, un espectador que recibe su propio abrigo? Reflexionando un poco se ve que el número f_n de permutaciones sin punto fijo de n abrigos se puede calcular a partir de f_n–1 y f_n–2:

f_n = (n − 1) · (f_n−1 + f_n−2)

Si se calculan estos números, empezando por f_n−1 y f_n−2, con 6 abrigos la proporción de permutaciones sin punto fijo ya es de alrededor del 36,7 % y apenas varía para números más grandes (la proporción es de 1/e, siendo e el número de Euler, del que ya se ha hablado repetidamente en el libro). Esto significa que la probabilidad de que al menos uno reciba el abrigo que le pertenece es del 63,3 %.

<<

[Solución ejercicio 9]

<<

[Solución ejercicio 10]

Dado que los fumadores mueren antes, son menos los miembros de este grupo que llegan a cumplir 65 años de edad. Por eso, el grupo de los no fumadores está «sobreenvejecido» y su riesgo de muerte es en total más alto.

También en este caso estamos ante una típica paradoja de Simpson. La tabla muestra que en todos los grupos de edad los no fumadores tienen más probabilidades de sobrevivir. El conjunto, en el que los fumadores parecen salir mejor parados, está distorsionado: son en general menos los fumadores que alcanzan los 65 años de edad que los no fumadores. Por eso, el grupo de los no fumadores es en promedio mayor que el de los fumadores y por esta sencilla razón y ninguna otra su riesgo de muerte es en total más alto.

<<

[Solución ejercicio 11]

Si el tramo que recorre Hasselhoff sobre la arena es s₁ y el que nada en el agua es s₂, el socorrista necesita en total el tiempo siguiente:

Con ayuda del teorema de Pitágoras se puede calcular el tiempo correspondiente para cada punto x en el que el socorrista se lanza al agua. Esto nos da una función t(x) cuyo valor mínimo podemos determinar.

Resultado: lo mejor es que corra hasta casi llegar al punto en que el tramo sobre el agua es más corto, o para ser exactos: debería lanzarse al agua 7,8 metros antes.

<<

[Solución ejercicio 12]

Con las fichas se puede salvar cualquier distancia.

También en este caso nos servimos de un truco: imaginemos que colocamos la segunda ficha debajo de la primera, luego la tercera debajo de la segunda, de manera que toda la estructura todavía se mantenga en pie. Si una ficha tiene una anchura de dos unidades, la segunda hay que introducirla debajo de la primera desplazada en una unidad. Las demás fichas se colocan con un desplazamiento de ¹/₂, ¹/₃, ¹/₄ de unidad y así sucesivamente. El aumento es cada vez menor, según la fórmula

pero la serie no tienen límite, de modo que con las fichas se puede salvar cualquier distancia.

<<

[Solución ejercicio 13]

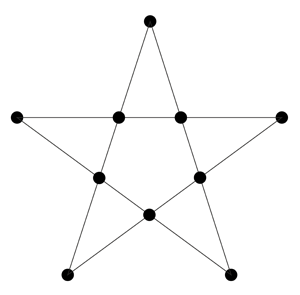
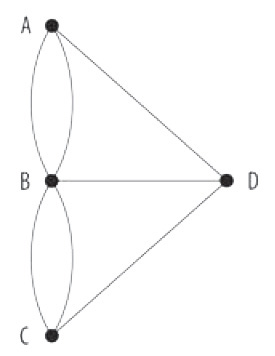
Este paseo dominical es imposible.

Para resolver el problema podemos representar las cuatro orillas A, B, C y D en forma de punto y cada puente en forma de línea que une los puntos correspondientes:

¿Podemos dibujar este gráfico con una sola línea sin levantar el lápiz del papel? Si esto fuera posible, como máximo debería haber dos puntos de los que parte un número impar de líneas (el punto de partida y el de llegada). En todos los demás puntos, por cada línea de acceso hay también una línea de salida. En el gráfico, sin embargo, de todos los puntos sale un número impar de líneas, de manera que el paseo dominical es imposible.

<<

[Solución ejercicio 14]

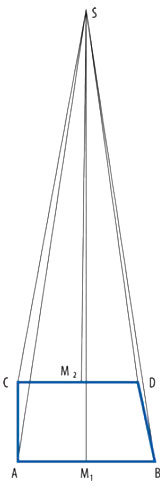
El error está en el dibujo. El punto S debería estar mucho más arriba y se saldría de la página. Así que presentamos aquí un gráfico con un ángulo recto y otro de unos 80 grados: el principio es el mismo. Se ve claramente que el triángulo BDS se halla «fuera» y con ello invalida toda la argumentación:

<<

[Solución ejercicio 15]

«La frecuencia de los tubos es inversamente proporcional al cuadrado de su longitud», y esto significa:

Si la frecuencia ha de ser dos veces mayor, el tubo ha de tener la longitud inicial dividida entre la raíz cuadrada de 2.

<<

[Solución ejercicio 16]

Los datos dan lugar a un sistema de ecuaciones con dos incógnitas. Si k es la edad del niño y m la de la madre, tenemos que

Podemos despejar la incógnita m en ambas ecuaciones

y sustituirla, obteniendo

La solución da una edad del niño negativa: −9 meses.

<<

[Solución ejercicio 17]

El radio de un círculo es la circunferencia dividida entre 2π. Si se alarga la cinta 1 metro, el radio crece ¹/_2π = 0,16 metros. Por tanto, la cinta se separa 16 centímetros de la superficie alrededor del globo, dejando espacio suficiente para que pase el ratón.

<<