Juez: Acusado, se le acusa de haber ofrecido en venta una droga, concretamente crack, a un agente de policía vestido de paisano en marzo de 2002 en el cruce de la calle 40 con la 8ª avenida.

Acusado: Eso ya lo he reconocido.

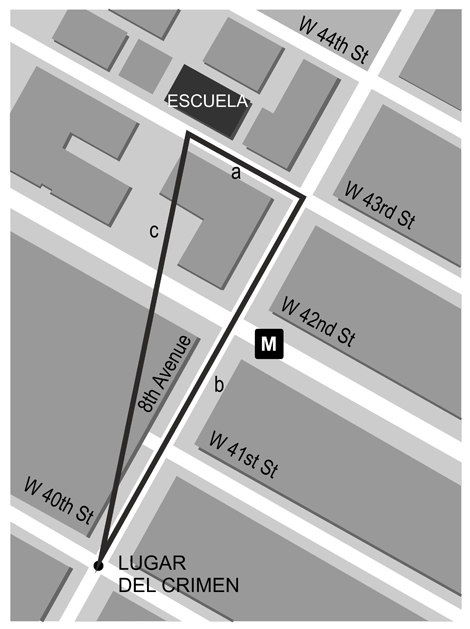
Juez: Pero hoy se trata de dilucidar si cometió usted un delito especialmente grave. Con arreglo al artículo 220 del Código Penal, el caso debe considerarse especialmente grave si el delito se comete en un recinto escolar o dentro de un radio de mil pies a la redonda de una escuela. Tengo aquí un plano de la ciudad donde está marcado el lugar en que fue usted detenido y la escuela más cercana, el colegio de Enseñanza Primaria Holy Cross, que se halla a tres manzanas de distancia. ¿Qué distancia hay exactamente entre los dos puntos?

Defensora: Del expediente de instrucción se desprende que la policía envió a un agente que midió la distancia recorriéndola a pie. Primero fue por la calle 43 y la 8ª avenida y midió 1.294 pies. Después tomó el atajo por el aparcamiento entre los edificios y la distancia fue de 1.091 pies. Este fue el camino más corto posible, y mide más de 1.000 pies, por lo que no se dan las condiciones para considerarlo un delito especialmente grave.

Fiscal: ¡Protesto, Señoría! Se trata de la distancia entre el lugar del crimen y la escuela, y eso no se mide enviando a un agente a que la recorra. Hay que medir la distancia en línea recta. ¿Tal vez recuerden ustedes el teorema de Pitágoras? Este teorema permite calcular la longitud de la hipotenusa de un triángulo rectángulo, siempre que se conozca la longitud de los otros dos lados, los llamados catetos.

Acusado: ¿Nos va a dar ahora una lección de mates, o qué?

Fiscal: Por suerte, las calles de Nueva York suelen cruzarse en ángulos rectos, de modo que tenemos aquí un caso muy sencillo, que podemos resolver incluso sin necesidad de un plano. (Señala el plano dispuesto sobre un caballete.) El tramo de la calle 43 que va de la escuela a la 8ª avenida, que es el lado a del triángulo dibujado en el plano, mide 490 pies. Las tres manzanas de la 8ª avenida entre las calles 43 y 40, el lado b, miden 764 pies. Para calcular la distancia c, que es la distancia en línea recta entre la escuela y el lugar del crimen, hemos de calcular la raíz cuadrada de la suma de los cuadrados de los catetos… (Escribe sobre un rotafolio situado junto al plano.) Para c tenemos

c = √a² + b² = √490² + 764²

= √240.100 + 583.696 = √823.796 ≈ 908

908 pies, es decir, claramente menos de 1.000. Por tanto, sí se dan las circunstancias de un delito especialmente grave.

Acusado: Distancia en línea recta, ¡no me haga reír! ¿Así que los alumnos vienen volando por el aire para comprarme drogas? (Su abogada defensora le propina una ligera patadita debajo de la mesa.)

Defensora: Señoría, este artículo tiene por objeto proteger a los niños de las actividades de los camellos interponiendo una distancia. La prueba práctica del agente de policía ha demostrado que el camino a pie, cualquiera que sea el itinerario, mide más de 1.000 pies, y por tanto se cumple la norma de protección.

Juez: ¿O sea que pretende usted que la distancia dependa de si hay edificios de por medio o no? ¿Tenemos entonces que comprobar cada vez si los edificios en cuestión estaban abiertos al público y el horario en que lo estaban y si era posible pasar por ellos para acortar la distancia?

Fiscal: Por cierto que hay numerosos precedentes en los que siempre se aplicó el teorema de Pitágoras, es decir, el criterio de la distancia en línea recta. Por ejemplo, en el Estado de Indiana, donde las tiendas de bebidas alcohólicas han de situarse a cierta distancia mínima de cualquier iglesia.

Acusado: ¡Ahí, ahí, esos son los peores traficantes!

Juez (golpeando con el martillo sobre la mesa): ¡Silencio! He decidido: se rechaza el recurso del acusado y se confirma la sentencia de la instancia inferior. El sentido de la ley es trazar un círculo alrededor de las escuelas en cuyo interior los niños deben estar protegidos de toda amenaza del narcotráfico. No es razonable que haya que tener en cuenta el estado de edificación del barrio en que se halla la escuela. La distancia de 1.000 pies, por tanto, debe interpretarse, conforme a lo estipulado por el teorema del señor Pitágoras, como la línea recta entre dos puntos. Se levanta la sesión.

EL TEOREMA MATEMÁTICO MÁS CONOCIDO

Aunque en este caso (auténtico) seguramente habría sido más fácil medir la distancia entre la escuela y el lugar del crimen sobre el mismo plano, el teorema de Pitágoras es tan conocido y elemental que se emplea incluso en la jurisprudencia. En otro caso judicial se aplicó cuando un preso se opuso a que le encerraran junto con otro preso en la misma celda, alegando que el mal olor del retrete le molestaba. Con ayuda del teorema de Pitágoras se midió la distancia en línea recta entre la litera superior y el retrete.

A la pregunta de, «ante un triángulo rectángulo, ¿Cuánto es a² + b²?», casi todas las personas responden espontáneamente «c²». El porcentaje de aquellos que son capaces de explicar también esta ecuación será probablemente mucho menor.

El origen del teorema no se conoce; lo único que se sabe es que no lo descubrió Pitágoras. Ya se utilizaba en el antiguo Egipto, donde existía el gremio de los «harpedonaptas», que trazaban perpendiculares con las llamadas cuerdas de doce nudos. En India se empleaban cuerdas similares, y también en China y Babilonia se conocían los llamados «triples pitagóricos», es decir, grupos de tres números enteros que obedecen al teorema de Pitágoras.

El famoso teorema, sin embargo, como ya se ha dicho, no procede de Pitágoras, el fundador de la hermandad que lleva su nombre (véase capítulo 9). Fue Euclides quien bautizó el teorema con el nombre del antiguo matemático y filósofo en su libro Los elementos, una recopilación de los teoremas geométricos de su época.

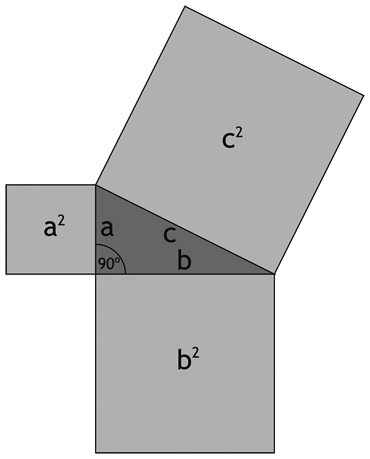
El teorema de Pitágoras habla de los tres lados de un triángulo rectángulo. «El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos». Otra de esas frases horribles del colegio, pero no hace falta memorizar cuál de los lados es la hipotenusa (ni cómo se escribe). «a² + b² = c²» es más fácil de recordar y con c se designa siempre el lado más largo del triángulo.

La ecuación se puede resolver despejando cualquiera de los lados a, b o c, lo que significa que si se conocen dos lados (y, por supuesto, uno de los ángulos, el recto) se puede calcular la longitud del tercer lado. Hay una generalización del teorema para todo tipo de triángulos, pero habría que usar las funciones angulares del seno y el coseno, lo que nos lleva a un nivel superior de la ciencia matemática. Sin embargo, el teorema también se aplica a muchas otras figuras geométricas. Un ejemplo lo tenemos en este mismo libro, en el capítulo 17. Un truco que casi siempre ayuda: si quiere demostrar usted algo en relación con una figura geométrica, descompóngala de alguna manera en triángulos rectángulos y aplique entones el teorema de Pitágoras.

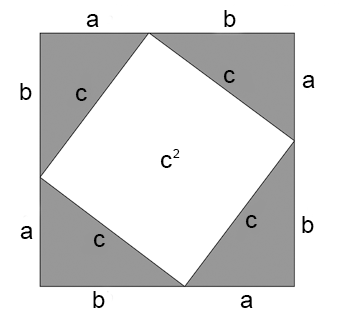
El teorema mismo se puede demostrar de cientos de maneras distintas; en un solo libro están recopiladas nada menos que 370. La que más me gusta es una demostración que mezcla geometría y álgebra. Hay que confeccionar (con papel o en la imaginación) cuatro triángulos rectángulos iguales y formar con ellos la siguiente figura:

Se obtiene un cuadrado de lado a + b que encierra en su interior otro cuadrado (vacío) de lado c. Si se comprende que con cada dos triángulos se puede formar un rectángulo de superficie a × b, entonces resulta que el cuadrado grande es igual a la suma del cuadrado pequeño y los cuatro triángulos, o sea

El primer miembro de la ecuación se resuelve fácilmente conforme a la conocida fórmula binomial (véase el apéndice).

Ahora solo queda restar 2ab de cada miembro de la ecuación y ¡ahí está!, el teorema de Pitágoras.

UNA MIRADA AL HORIZONTE

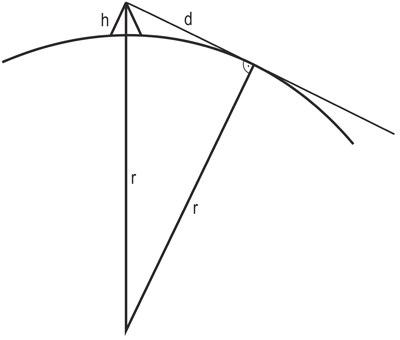
Para terminar veremos una aplicación del teorema que permite calcular la distancia del horizonte cuando se mira, por ejemplo, desde una cumbre de 1.000 metros de altitud hacia el mar.

Si la Tierra fuera plana, nuestra mirada podría alcanzar en principio hasta el infinito, pero en una esfera su alcance está limitado por la curvatura de la superficie. Nuestra mirada «roza» la superficie terrestre en el punto más alejado, y la línea recta entre el ojo y el horizonte es una tangente sobre la esfera, que por tanto forma un ángulo recto con el radio del planeta en ese punto. Así que ya tenemos un triángulo rectángulo en el que aparece el radio terrestre r, la altitud h desde la que miramos y el alcance d de nuestra vista. Así que podemos aplicar directamente el teorema de Pitágoras despejando la incógnita d²:

El radio de la esfera terrestre mide unos 6.400 kilómetros y la altitud h, en nuestro ejemplo, 1.000 metros. En la ecuación, por tanto, h² es insignificante en comparación con 2rh y para pequeñas alturas se puede ignorar (otra de esas típicas «licencias» asombrosamente frecuentes en el por lo demás tan preciso mundo de la matemática):

Así que si miramos desde la montaña de 1.000 metros de altitud hacia el horizonte, nuestra vista alcanza hasta unos 113 kilómetros de distancia. En Hawái hay un monte de 4.000 metros de altitud muy cerca del mar, el Mauna Kea, y según la ecuación la vista alcanza desde la cumbre hasta el doble de distancia, es decir, 226 kilómetros.

También podemos utilizar valores menores en la misma ecuación, por ejemplo la altura de los ojos de una persona que está en la playa. Suponiendo que es de 1,60 metros, es decir, 0,0016 kilómetros, el horizonte que ve se halla a tan solo 4,5 kilómetros de distancia.

EN LAS CALLES DE MANHATTAN

EL TEOREMA MATEMÁTICO MÁS CONOCIDO

UNA MIRADA AL HORIZONTE