Placa a bordo de las Pioneer 10 y 11. Cortesía de NASA/JPL.
Es tranquilizador saber que si alguna vez detectamos una transmisión involuntaria de alguna civilización extraterrestre, contaremos con ciertas herramientas matemáticas para enfrentarnos a semejante reto. Pero, desde el punto de vista criptográfico, resulta mucho más interesante cuando el intento de comunicación es voluntario. Para comunicarse voluntariamente con otra especie inteligente, el lenguaje natural no es la mejor elección, y son diferentes los enfoques que nuestros científicos se han planteado para intentar que la humanidad se haga entender.
A principios de la década de los setenta, se realizó el primer intento serio por parte de la comunidad científica de comunicarse con posibles inteligencias allende nuestro Sistema Solar. Estaban a punto de ser lanzadas dos nuevas sondas de la exitosa serie Pioneer de la NASA, las Pioneer 10 y 11, dos naves gemelas diseñadas para embarcarse en una ambiciosa misión de reconocimiento del Sistema Solar exterior. Sus altas velocidades iban a hacer de ellas los primeros objetos creados por el hombre destinados a escapar para siempre del Sistema Solar y adentrarse en lo más profundo del espacio interestelar. Este hecho sin precedentes sugirió la idea de que estas naves, como si fueran botellas lanzadas por un náufrago, llevaran en su interior un mensaje destinado a aquellos seres que pudieran un día encontrarlas.
La idea original provino de un periodista del Christian Science Monitor llamado Eric Burgess, que asistió a los tests finales de la Pioneer 10 en la cámara de vacío. Mirándola a través de los cristales de la cámara, se la imaginó como el primer emisario de la humanidad a las estrellas. Esa nave podría llevar un mensaje: «una vez existió un planeta llamado Tierra en el cual evolucionó una especie inteligente que pudo pensar más allá de su tiempo y más allá de su Sistema Solar». Con esta idea se dirigió al profesor Carl Sagan, entonces director del Laboratorio de Estudios Planetarios de la Universidad de Cornell. Sagan se entusiasmó con la idea y se puso inmediatamente en contacto con la oficina de proyectos de la Pioneer 10. Afortunadamente, la sugerencia fue acogida por el equipo de la Pioneer con igual entusiasmo y dieron luz verde a la iniciativa.
Se decidió así incorporar a bordo un mensaje grabado en una placa metálica de aluminio anodizado en oro, que en las condiciones del espacio tendría una durabilidad de cientos de millones de años. La opción que finalmente se tomó para el mensaje interestelar no fue ningún tipo de texto, escrito en alguna clase de caracteres codificados, sino que fue de tipo pictórico. Es decir, un dibujo. Sagan, junto con esposa Linda Salzman Sagan (quien fue de hecho la mano que realizó los dibujos) y el profesor Frank Drake de la Universidad de Cornell (el mismo Frank Drake del proyecto Ozma), se encargaron de diseñar una placa de 15 × 23 cm que iría sujeta al soporte de la antena de la nave, y cuyo diseño daría la vuelta al mundo:
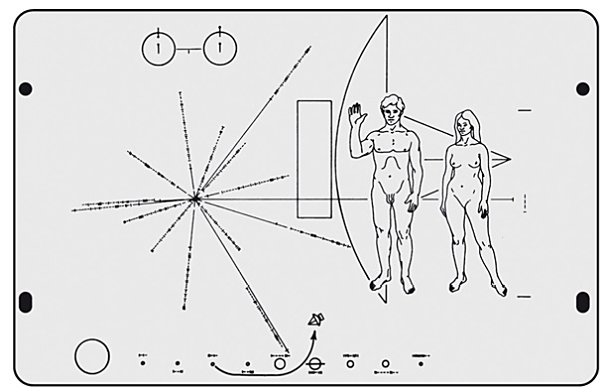
Placa a bordo de las Pioneer 10 y 11. Cortesía de NASA/JPL.
El dibujo mostraba en primer plano a una pareja humana de rasgos raciales indeterminados, a fin de que fuera representativa de toda la humanidad. Como gesto de amistad, el hombre saludaba con una mano en alto al posible alienígena que viera el dibujo en un futuro remoto. Tras ellos había un esbozo de la antena de la Pioneer, a fin de dar una idea del tamaño de los seres humanos representados. Se representaron ambos sexos para mostrar que el sistema de procreación de nuestra especie (como el de buena parte de la vida en la Tierra) es la reproducción sexual, aunque la pareja no se cogía de las manos a fin de no parecer un ser de cuatro piernas y dos cabezas.
En la parte superior vemos dos dibujos en forma de esferas que simbolizan la transición entre dos estados del átomo de hidrogeno, el más abundante del Universo. Como vimos, esta transición emite una onda de radio con una longitud de onda de 21 cm, que da la escala de las dimensiones en el dibujo. Así, a la derecha de los seres humanos, figura el símbolo | − − −, equivalente a 1000 (la línea vertical representa un 1 y la horizontal un 0) que en el sistema numérico binario corresponde al 8 del sistema decimal. Es decir, esas cuatro rayitas junto a los seres humanos indican que la altura de éstos es 8 veces 21 cm, o sea unos 168 cm.
Debajo figura una representación esquemática de nuestro Sistema Solar, que muestra cómo la sonda Pioneer parte del tercer planeta. Junto a cada planeta figura un número en binario que da la distancia de los planetas al Sol, aunque ahora la escala no es ya la longitud de 21 cm, sino una longitud mucho mayor: la décima parte del radio de la órbita de Mercurio. Así, junto a la Tierra vemos que figura el símbolo | | − | −, o lo que es lo mismo, 11010, que en binario es el número 26. Es decir, la Tierra está 2,6 veces más lejos del Sol que Mercurio.
Por último, la «estrella» de líneas a la izquierda es un diagrama de la posición y los ritmos de catorce púlsares, en relación con la Tierra y el centro de la Galaxia, para indicar la localización de nuestro planeta. Los períodos de cada púlsar están dados por un número binario a lo largo de cada línea, y la longitud de la línea debe dar una idea de la distancia de cada púlsar a la Tierra. Como ya hemos visto, el período de un púlsar es muy preciso y tan característico como una huella dactilar, aunque debido a que se van frenando muy poco a poco, aumenta lentamente con el tiempo. La idea era que, de esta manera, si los receptores de la placa conseguían identificar algunos de los púlsares y calculando cómo habían aumentado sus períodos de pulsación, podrían determinar además cuánto hacía que fue mandada la nave. Por último, la posición del centro de la Galaxia está representada por una quinceava línea horizontal que sale hacia la derecha y pasa por detrás de los dos seres humanos.
Irónicamente, esta iniciativa de un mensaje de buena voluntad entre civilizaciones levantó un enorme revuelo de opiniones enfrentadas dentro de nuestra civilización sobre que un pequeño grupo decidiera por toda la humanidad el contenido del mensaje, sobre el «riesgo» de revelar a extraterrestres hostiles nuestra situación en la Galaxia o sobre el escaso contenido científico del mensaje. Pero las más airadas fueron, en el seno de la tolerante sociedad estadounidense, las relativas a la ¡desnudez de la pareja! y llegaron a recibirse encendidas cartas sobre «pornografía científica» y el envío de «obscenidades a las estrellas». Incluso periódicos como el Chicaco Sun Times o el Inquirer de Filadelfia retocaron en sus ediciones la imagen de la placa para que no se mostraran los genitales. A pesar de las críticas, las naves Pioneer 10 y 11 fueron lanzadas desde Cabo Cañaveral el 3 de marzo de 1972 y el 6 de abril de 1973, respectivamente, llevando consigo su mensaje a las estrellas.
Pero las viejas Pioneer no son las únicas embajadoras de nuestra especie. Otras dos veteranas se atreven también a desafiar los fríos del espacio interestelar portando otro mensaje. Se trata de las dos naves Voyager, también destinadas a alejarse para siempre del Sistema Solar. La primera nave en salir fue la Voyager 2, que fue lanzada desde Cabo Cañaveral el 20 de agosto de 1977. La Voyager 1 fue lanzada dos semanas después, el 5 de septiembre, en una trayectoria más rápida y corta, por lo que pese a ser la segunda en salir, sería la primera en llegar a Júpiter. Viajando a una velocidad de 63.000 km/h, se convirtió en el objeto más rápido fabricado por la humanidad. En febrero de 1998 alcanzó y rebasó a la Pioneer 10 y hoy día ostenta otro récord: es nuestra nave a mayor distancia de la Tierra.
Dado el enorme éxito de público que, pese a todo, supuso el mensaje de las Pioneer, cuando las naves Voyager se proyectaron, la NASA planeó incorporar también en estas naves un mensaje a los posibles seres extraterrestres que las pudieran encontrar. El director del proyecto Voyager le pidió a Carl Sagan que organizara de nuevo la tarea de colocar un mensaje a bordo de las sondas. El comité dirigido por Sagan diseñó esta vez un mensaje más ambicioso, rico y complejo, una especie de cápsula de tiempo que contara la historia de nuestro mundo. Esta vez, en lugar de en una placa, el mensaje se grabó en un disco fonográfico de oro. Para protegerlo, el disco se encapsuló bajo una cubierta con instrucciones grabadas para su funcionamiento, así como los mismos diagramas de la transición del hidrógeno y de los períodos de púlsares que iban en la placa de las Pioneer.
El disco contiene, codificada, una enorme variedad de sonidos, incluyendo música de diferentes culturas, sonidos de la naturaleza, saludos en todas las lenguas humanas y 115 imágenes, constituidas por dibujos, diagramas científicos y fotografías de la Tierra, tanto en blanco y negro como en color (por supuesto, la NASA no permitió incluir la fotografía de ningún desnudo). En definitiva, una selección que daría buena idea de la diversidad de vida y culturas del planeta, y de la ciencia y conocimientos de la humanidad…
… Si el receptor conseguía descifrarlo. Porque, como vimos, una inteligencia no humana podría tener problemas para comprender las imágenes bidimensionales y los colores, y por tanto para entender el mensaje (los problemas de comprensión no se limitan a los alienígenas: ¡muy pocos científicos consiguieron descifrar los diagramas de la placa de las Pioneer sin ayuda!). Entonces, ¿por qué se eligieron este tipo de formatos para los mensajes de las Pioneer y Voyager? La respuesta es que en realidad no se cree que estas naves sean nunca interceptadas, dado lo inconmensurablemente enorme y vacío que es el espacio interestelar y lo absurdamente remotas que son las posibilidades de que encuentren algún planeta. No digamos ya uno habitado por una civilización.
Disco Los Sonidos de la Tierra de las Voyager, cubierta de protección con instrucciones de reproducción y una selección de las imágenes que éste lleva.
El verdadero destinatario de estos mensajes es la humanidad. Su función real es estimular el espíritu humano de exploración, hacernos concebir la esperanza de que es posible el contacto con otras civilizaciones de nuestra Galaxia. Hay algo profundamente humano en el intento, en el mero hecho de intentar esta comunicación, en dejar esa huella nuestra imperecedera para la posteridad. Hasta cierto punto colma nuestras ansias de perdurar. Hemos escrito con letra pequeña en el gran lavabo de la Galaxia «La humanidad estuvo aquí». Y ¿quién sabe?, es posible incluso que seamos nosotros mismos los que, un día, en un futuro lejano, leamos estos mensajes de cuando nuestra civilización era joven y todavía no conocía los viajes interestelares.
Cero cero cero cero cero cero uno cero uno cero… ¿perdón?, ¿cómo?, ¿qué no entiende lo que le digo? Pues lo que acaba de leer no es otra cosa que la primera frase del mensaje de radio destinado a otras civilizaciones más famoso del mundo: el radiomensaje de Arecibo, emitido a las estrellas en 1974 desde el observatorio de Arecibo, Puerto Rico, donde como recordaremos está emplazado el radiotelescopio más sensible del mundo.
En 1974 se había realizado la obra faraónica de poner un nuevo recubrimiento reflectante a esta antena de 305 metros de diámetro, con lo que se incrementaba su sensibilidad. También se le había añadido un nuevo transmisor, de medio millón de watios de potencia. De repente, con esta combinación, la antena estaba capacitada para emitir una señal de radio que podría ser millones de veces más intensa que la emisión del Sol en la misma frecuencia. Es decir, con potencia suficiente para ser fácilmente detectada incluso desde el otro extremo de la Galaxia. Si la antena emitía tal señal, cualquiera que estuviera mirando hacia el Sistema Solar en esas frecuencias podría detectar con facilidad la señal de radio y distinguir claramente el planeta Tierra.
Por ese motivo, se pensó que la ceremonia inaugural de la remodelación del radiotelescopio, además de en palabras de políticos y en canapés, consistiera en la emisión de una señal de radio a las estrellas que contuviera un mensaje de nuestro mundo. Así, el día de la ceremonia, el sábado 16 de noviembre de 1974, a la una del mediodía hora local, la antena del radiotelescopio apuntó hacia el cúmulo de estrellas M13 en la constelación de Hércules, y comenzó a radiar su mensaje. La emisión, que duró poco menos de tres minutos, consistió en dos tipos distintos de «pitidos» de radio de frecuencias en torno a 2.380 MHz, que representaban unos y ceros (los ceros tenían una frecuencia ligeramente por debajo de ese valor y los unos, ligeramente por encima). Al mismo tiempo que el mensaje interestelar se radiaba, los cerca de doscientos asistentes a la ceremonia podían escucharlo (convenientemente transformado a frecuencias audibles) a través de los altavoces. Cuando éstos empezaron a sonar, buena parte del público salió al exterior a mirar cómo la inmensa antena emitía su grito a las estrellas. Cuando el mensaje concluyó, había lágrimas en algunos ojos. El mensaje que había provocado semejante emoción era éste:
En total, 1.679 bits de información, expresados aquí como caracteres numéricos. ¿Pero qué quiere decir todo ese montón de unos y ceros, cómo descifrar este mensaje? La solución la encontramos en las matemáticas, y ese número, el 1.679, tiene la clave para iniciar el proceso de descifrado, pues 1.679 es un número un tanto especial: es el producto de los números primos 23 y 73. Para entender qué tiene esto de especial, comparémoslo con el número natural que le sigue en orden, el 1.680. Este otro número es igual a 16 × 105, o a 15 × 112, o a 35 × 48, o a 21 × 80 o a 30 × 56…, es decir, existen diferentes maneras de representarlo como el producto de dos números enteros (concretamente, hay 19 maneras). Pero 1.679 sólo puede representarse como el producto de esos dos números primos, 23 y 73.
A partir de este hecho, el receptor deberá ser capaz de deducir que el cúmulo de ceros y unos que ha recibido se tiene que representar como una matriz bidimensional de 23 × 73 elementos. Es decir, que es una imagen. Y en efecto, cuando ordenamos la anterior serie de números de manera que en cada renglón haya sólo 23 dígitos, obteniendo un «texto» con 73 renglones, podemos ver que en su interior los unos y ceros forman una imagen (para realzarla, he mostrado los unos en negrita):
Radiomensaje de Arecibo de 1974.
Junto a ella, a su derecha, vemos la imagen que surge si pintamos de negro los bits de valor uno y de blanco los de valor cero. Posiblemente, a simple vista seamos ya capaces de reconocer algunas cosas en esta imagen, pero su contenido total de información es bastante alto, y merece la pena que nos detengamos a estudiar en de-talle este famoso ejemplo de mensaje interestelar, tan imitado en algunos aspectos por mensajes posteriores. En la cabecera de la imagen aparece un convenio para representar los números del 1 al 10 en binario. Es importante que éste quede claro para que se entienda el resto del mensaje: el píxel negro de abajo del todo de cada número sólo representa el inicio del número, pero no contiene ningún valor numérico. Sobre él se sitúa el verdadero número binario (siempre con negro = 1 y blanco = 0), de forma que 
representa el número binario 10, es decir, el 2 decimal. Por comodidad, el número no se representa de forma indefinida hacia arriba, sino que se puede truncar en dos o más filas consecutivas (pero siempre situándose sobre el píxel de referencia), de manera que el último, el 
, corresponde al número binario 1010, es decir, al 10 decimal.
Una vez entendido este criterio numérico, es fácil leer en la siguiente parte del mensaje los números 1, 6, 7, 8 y 15. Con un poco de imaginación se puede adivinar que se trata de los números atómicos de los elementos hidrógeno, carbono, nitrógeno, oxígeno y fósforo (H, C, N, O, P). Es decir, los elementos más abundantes en la composición de los seres vivos. A continuación se muestran, en forma de números, una serie de curiosos dibujos que resultan ser fórmulas químicas de especial importancia. Por ejemplo, el primer dibujo, 
, corresponde a cinco números: 7, 5, 0, 1 y 0. Si asumimos que esos cinco números representan proporciones de los cinco elementos anteriores, en el mismo orden que aparecen, vemos que se trata de la molécula H7C5O1, es decir, la desoxirribosa. Bajo ella está el fosfato (
= 0, 0, 0, 4, 1; o lo que es lo mismo, O4P), bajo ella de nuevo la desoxirribosa y bajo ella otra vez el fosfato. Y esa misma cadena de cuatro moléculas aparece también en el margen derecho de la imagen. En medio de ambas cadenas, como en un bocadillo, hay otras cuatro moléculas que, siguiendo el mismo criterio, corresponden a la adenina (H4C5N5), timina (H5C5N2O2), citosina (H4C4N3O) y guanina (H4C5N5O), o sea, las bases nitrogenadas del dna. Es decir, lo que representa ese conjunto de iconos es la estructura básica del DNA:
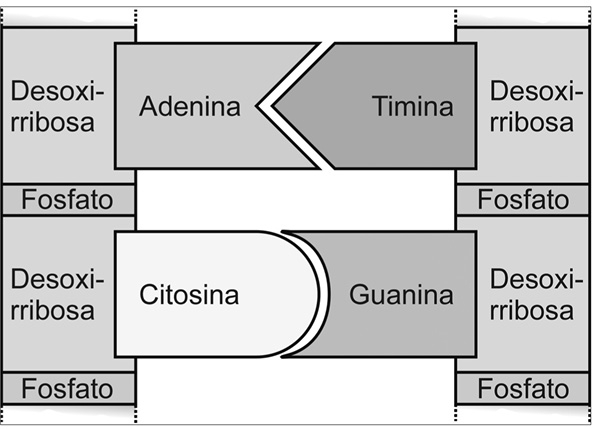
Estructura del DNA y complementariedad de las bases, representada en el radiomensaje de Arecibo.
Lo siguiente que podemos ver es una representación gráfica de la doble hélice del DNA, que arranca como continuación de esta estructura, lo que da a entender que ésa es la composición química de la doble hélice. En medio de ella, cortándola por la mitad, aparece un nuevo y enorme número en binario, del orden de los 4.300 millones, que indica la cantidad de nucleótidos que constituyen el DNA.
El dibujo de la molécula del DNA termina sobre la cabeza de una figura que representa a un ser humano, flanqueada por dos números en binario (en esta ocasión tumbados hacia la derecha). El de su derecha es un número muy grande, del orden de los 4.000 millones, que corresponde a la población humana el día en que se envió la señal. El de su izquierda indica la altura de la figura humana: 14. ¿Pero 14 qué? En ningún sitio se ha definido aún ninguna unidad de longitud ¿cuál deberá tomar la inteligencia que decodifique el mensaje? La única de la que puede echar mano es la propia longitud de onda de la señal. Vimos que su frecuencia de emisión era de 2.380 MHz. Como en una onda se cumple que su velocidad (en este caso, la de la luz) es igual al producto de su frecuencia por su longitud de onda, el lector puede fácilmente calcular que la longitud de onda es de 12,6 cm. Es decir, que la altura del ser humano del mensaje es 14 veces 12,6 cm: unos 176 cm.
Justo debajo del dibujo de la persona figura un esquema del Sistema Solar, con el Sol a la izquierda, dando la idea de que el quinto y sexto planeta (Júpiter y Saturno) son los más grandes, y que el tercero (la Tierra) tiene una especial importancia para nosotros. De hecho, el ser humano está justo sobre él. Por último está un dibujo esquemático de la antena de Arecibo, emitiendo su señal, y bajo ella otro número binario (en esta ocasión tumbado hacia la izquierda), el 2.430, que indica el diámetro de la antena: 2.430 × 12,6 cm = 306 metros.
En definitiva, una enorme cantidad de información apretada en muy poco espacio, que presenta obvias dificultades de interpretación (no a todos se nos ocurrirían los pasos aquí explicados, ni queda claro cómo diferenciar lo que son números de lo que no lo son, ni sus arbitrarios cambios de dirección). Pero además hay en este mensaje asunciones implícitas que probablemente pasaron desapercibidas durante su elaboración. Por ejemplo, en el dibujo de la antena de Arecibo, entresacado en la siguiente imagen, queda claro a nuestros ojos que lo remarcado con un cuadrado es una línea en diagonal:
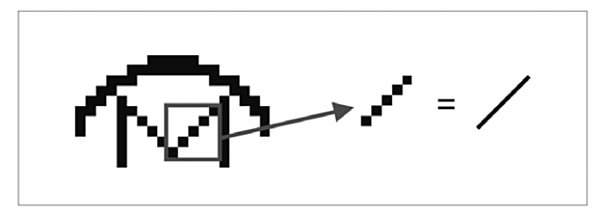
Pero ambas imágenes nos parecen equivalentes porque tenemos en nuestro córtex visual neuronas «identificalíneas» que, como ya vimos, no se dedican a otra cosa más que a encontrar de manera automática alineaciones. En realidad, ambas cosas son muy distintas, y la imagen de la izquierda no es más que un conjunto de cinco cuadrados negros dispuestos en una peculiar formación.
Otra asunción implícita está en la manera de reordenar los unos y ceros del mensaje. Para empezar, podríamos haber reordenado los 1.679 elementos en una matriz bidimensional 73 × 23, en vez de en una 23 × 73, con lo que habríamos obtenido una imagen como ésta:
Radiomensaje de Arecibo de 1974, reordenado.
que para nuestros ojos resulta ser un sin sentido (¿aunque quizá no para unos ojos alienígenas?). En realidad, este problema de elegir entre dos posibles reordenaciones se podría haber evitado fácilmente si el número de bits que se hubiera enviado hubiera sido el cuadrado de un único número primo, trabajando con una imagen cuadrada en vez de rectangular. Por ejemplo, sólo avanzando dos números naturales más se hubiera llegado al número 1.681, que resulta ser 41 × 41.
Pero aun así, tanto en un caso como en otro, hemos asumido que los elementos se disponen rellenando ordenadamente de un lado a otro una fila, hasta que se llena, y luego continuamos en la siguiente en la misma dirección hasta que se vuelve a llenar, etc.; es decir, de forma análoga a como escribimos. Y aunque es cierto que ordenando así los elementos se simplifican mucho las cosas cuando trabajamos con índices y matrices en matemáticas o en programación, esa forma de ubicar píxeles en una imagen no deja de ser una mera asunción que se hace. Éste no tiene por qué ser el orden natural para otra civilización, sobre todo si no ha desarrollado matemáticas matriciales. Quizá para ellos resulte más lógico hacerlo en zigzag (como los textos antiguos en bustrofedón), o en espirales (como en el disco de Festo, por seguir con las analogías de textos escritos). O quizá, aunque tengan representaciones bidimensionales análogas a nuestras imágenes, no las representen dentro de estructuras rectangulares o cuadradas, sino quizá en círculos, triángulos, hexágonos, o quizá incluso en tres dimensiones…
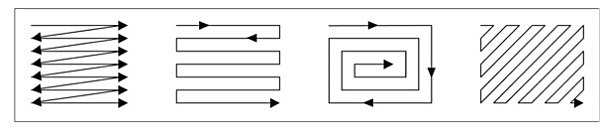
Diferentes formas de emplazar píxeles en una imagen bidimensional rectangular. A la izquierda, la usada en la codificación de la imagen de Arecibo.
Por si ello fuera poco, además, la civilización alienígena que detecte la señal deberá tener la suerte de recibirla toda de una sola vez, para tener alguna posibilidad de descifrarla. Por desgracia, el mensaje de Arecibo no se envió repetidamente (recordemos lo que vimos sobre las características que debería tener una señal de llamada), sino una única vez; con solo que se perdieran un simple bit de información, los receptores ya no contarían con la mágica cifra de 1.679 bits que les permitiría deducir que lo que han recibido es una imagen y comenzar el proceso de descifrado. Los habitantes de M13 van a tener que estar muy atentos dentro de 25.000 años.
Pese a sus defectos, el mensaje de Arecibo nos ha mostrado una de las claves que se debe tener en cuenta para obtener éxito en nuestros intentos de comunicación con otras inteligencias: el uso de números como base del mensaje. Como vimos cuando definimos el proceso de comunicación, para que sea posible un intercambio de información entre dos inteligencias, hay de contar con un código compartido por ambas partes. Un lenguaje común. Pero ¿es posible elaborar un lenguaje de intercambio con una civilización extraterrestre, completamente alienígena en absolutamente todos los aspectos? Hay científicos que creen que sí, si para ello se parte de bases comunes sobre las que desarrollar ese lenguaje. ¿Y qué podemos tener en común con ellos?
Por supuesto, la primera cosa que compartimos son las leyes naturales; tanto ellos como nosotros vivimos en el mismo Universo, y estamos sometidos a las mismas leyes de la naturaleza. Incluirlas de algún modo en la elaboración de un lenguaje de comunicación aumenta las probabilidades de que éste sea entendible (esta consideración ya aparecía, como hemos visto, en el mensaje de Arecibo, aunque de una forma bastante naíf). La otra es las matemáticas (y la lógica), gracias a su cualidad platónica de conocimiento universal. La razón entre el perímetro y el diámetro de una circunferencia es siempre el mismo número (pi), sea cuál sea el tamaño de esa circunferencia. Y 41 es un número primo, independientemente de las culturas, ideologías o civilizaciones. Precisamente a través de la lógica y las matemáticas será como se elabore una estructura y gramática para ese lenguaje.
Y aquí es donde surge el primer pero. Porque si bien es obvio que los seres vivientes de todo el Universo estamos sometidos a las mismas leyes de la naturaleza, no queda tan claro que las civilizaciones extraterrestres compartan con nosotros las matemáticas. No ya los tipos de matemáticas que hacemos los humanos (geometría, análisis, álgebra…), sino el mero concepto de matemáticas en sí. Tal vez seamos la única especie inteligente del Universo que las ha desarrollado. Quizá la famosa universalidad de las matemáticas no sea más que un mito, después de todo.
De nuevo, la única guía que tenemos para estimar las posibilidades de que inteligencias extraterrestres posean algún tipo de matemáticas es volver los ojos a la vida animal de nuestro mundo. Por supuesto, no vamos a buscar en nuestros compañeros de planeta la posesión de ningún tipo de matemáticas en el sentido estricto (¿exceptuando quizá a los delfines?), sino ver cómo andan de fuertes en los conceptos fundamentales que son las bases con las que hemos construido las matemáticas: espacio, conjuntos, números, distancia…
Y las perspectivas son alentadoras. Para empezar, muchos animales, al mostrarles dos montones distintos de comida, se dan cuenta de cuál es el más grande, y por supuesto van a comérselo. Tal vez esto le parezca al lector una obviedad, pero ha de tener en cuenta que la noción mayor que es un concepto matemático legítimo.
Más aún. En la naturaleza encontramos numerosos animales (roedores, monos, aves y un largo etcétera) que muestran poseer la habilidad aritmética más elemental: saben contar. Las gallinas saben cuántos huevos tiene su puesta. Y se puede entrenar a las ratas de laboratorio para que cuenten estímulos externos (como toques de silbato o destellos de luz) y que respondan tocando un pulsador sólo después de un número determinado de éstos. Es un resultado general de tales experimentos que estos animales contadores son capaces de discriminar con gran precisión entre cantidades pequeñas, si bien pierden esta habilidad cuando se enfrentan a cantidades grandes muy similares. Aunque si estas cantidades grandes son lo suficientemente distintas, consiguen distinguirlas. Así, en pruebas realizadas con palomas entrenadas para que picoteen un número determinado de veces a cambio de una recompensa, se ha visto que diferencian consistentemente 4 picotazos de 5 picotazos, pero fallan a la hora de discriminar entre 49 y 50; sin embargo, distinguen sin problemas 40 de 50.
Rizando más el rizo, encontramos animales que pueden efectuar operaciones elementales con números enteros a niveles sorprendentes. La chimpancé Sheba fue entrenada para que identificara correctamente cantidades enteras con ¡los caracteres arábigos numerales correspondientes! Es decir, que entendía perfectamente que por ejemplo el símbolo escrito 4 representaba la cantidad de cuatro objetos, cualesquiera que fueran. En un experimento se la dejó en una habitación donde había naranjas guardadas en dos lugares distintos. Sheba debía ir a ambos lugares, ver las naranjas que había en cada uno de ellos, y después indicar el numeral correspondiente a la suma de ambas cantidades. Lo que hizo correctamente en todas las ocasiones, demostrando que, además de contar, tiene la capacidad de sumar. Pero las habilidades de Sheba van más allá; se ha demostrado que incluso es capaz de sumar entre sí directamente caracteres numerales, es decir, que al mostrarle dos caracteres escritos (por ejemplo 3 y 2), señala consistentemente el numeral correspondiente a la suma (en este ejemplo, el 5). De todas formas, los chimpancés son los parientes más cercanos al hombre, y estos llamativos resultados se han conseguido tras un entrenamiento intensivo. ¿Qué encontraremos en parientes más lejanos que no hayan sido entrenados?
Para estudiar las capacidades de realizar operaciones matemáticas de los animales al natural, podemos echar mano de su perplejidad ante operaciones matemáticas erróneas. En un interesante experimento de los investigadores Hauser y Carey, a un grupo de macacos salvajes se les mostraba dos berenjenas (unos objetos que resultaban novedosos e interesantes para ellos) que luego se ponían sobre una plataforma tapadas por una pantalla. Después se retiraba la pantalla y en algunos casos se les mostraba las dos berenjenas, mientras que en otros se les mostraba sólo una berenjena (la otra se había escamoteado de detrás de la pantalla), o tres (se había añadido a escondidas otra). En las ocasiones en que aparecía un número erróneo de berenjenas en la plataforma, los monos mostraban extrañeza y el tiempo en que se quedaban mirando con perplejidad la plataforma era mucho mayor que en el caso en que el número de berenjenas era el correcto. Es decir, se daban cuenta de que 1 + 1 debe ser igual a 2.
El experimento se repitió también con la sustracción: tras mostrarles dos berenjenas y ponerlas tras la pantalla, se extraía después de detrás de la pantalla una de ellas de manera ostentosa. En las ocasiones en que al retirar la pantalla había dos berenjenas, el tiempo de observación fue de nuevo mucho mayor que en el caso en que había el número correcto de berenjenas (o sea, una). Es decir, que estos macacos salvajes se daban también cuenta de que el resultado correcto de la operación 2 − 1 debía ser 1. Este tipo de experimentos se ha repetido con idénticos resultados con los tamarinos, unos pequeños monos del nuevo mundo emparentado con los titís, mucho más alejados genéticamente de nosotros.
Grupo de macacos acicalándose: unos parientes cercanos con sorprendentes habilidades aritméticas.
En resumen, numerosos animales manifiestan, tanto en pruebas de laboratorio como en su comportamiento natural, las habilidades aritméticas más básicas (contar, sumar y restar). Esta convergencia evolutiva entre especies tan diversas indica que existe una presión selectiva a favor de la adquisición de esas capacidades matemáticas elementales. Y es que, de hecho, saber contar, sumar y restar ofrece una clara ventaja a la especie que sabe hacerlo. Un simple ejemplo basta para darnos cuenta. Imaginemos esta escena: un animal de regreso a su madriguera ve entrar en ella una manada de cuatro lobos. Ante esta amenaza se quedará fuera, expectante a que los depredadores se marchen. Según vayan saliendo éstos, si el animal posee habilidades aritméticas, en su cerebro se dará un proceso análogo al siguiente: «Bueno, han entrado cuatro y ahora sale uno, ya quedan tres. ¡Ah, ahora sale otro!, todavía quedan dos. Otro más sale ¡ya sólo queda uno! ¡Bien!, ahí sale otro más, el último. Ya no queda ninguno, puedo entrar en mi madriguera». Mientras que si no las posee, el proceso será más bien algo como: «Bueno, ha entrado un grupo de lobos. ¡Ahora sale uno! Esperemos un poco más. ¡Ahí sale otro! vale, ya quedan menos. ¡Otro más sale! Bueno, pues yo creo que ya se han ido todos. Voy a entrar a mi madriguera», con el trágico desenlace que todos imaginamos. De esta forma, se selecciona la supervivencia de los animales con capacidad para contar, sumar y restar.
En cuanto a otros conceptos físico-matemáticos básicos como el espacio, la distancia o la noción de mayor o menor que, cualquier animal que posea un análogo mental de estos conceptos tendrá una obvia ventaja frente a los que no lo posean, por ejemplo a la hora de anticiparse un depredador al movimiento de su presa (o viceversa), elegir la fruta que proporcione más alimento o calcular distancias en un salto arriesgado. La existencia de esta presión selectiva, y la consecuente convergencia evolutiva que produce en distintos animales, es un fuerte respaldo a que conceptos matemáticos similares existan en la mente de seres extraterrestres inteligentes, y apoya el uso de las matemáticas para la elaboración de un lenguaje de comunicación.
Pero si los beneficios de la aritmética elemental son evidentes, no todos los conceptos matemáticos proporcionan ventajas selectivas, por lo que la probabilidad de que compartamos con otros animales o con inteligencias extraterrestres otras nociones matemáticas es menor. Por ejemplo, los humanos sabemos contar, sumar y restar pequeñas cantidades prácticamente de forma innata, pero nos vemos obligados a memorizar las tablas de multiplicar, debido a que no ha habido ninguna presión selectiva que favorezca poseer esa habilidad. Por ese motivo, la capacidad de multiplicar números tenemos que construirla posteriormente a partir de las otras bases matemáticas que sí poseemos.
Es relevante contar aquí un interesante resultado obtenido mediante algoritmos genéticos. Un algoritmo genético es un programa de ordenador cuyo funcionamiento se optimiza a partir de un proceso de «selección darwiniana» análogo al que se produce en la naturaleza. El programa se ve enfrentado a un problema, a partir del cual produce una respuesta. El programa crea programas hijo, copias de sí mismo, pero con ligeras modificaciones, introducidas al azar aquí o allá, para simular los procesos de mutaciones aleatorias que sufre el DNA de los seres vivos. Estos hijos se ven sometidos de nuevo ante el problema y producen su propia respuesta. Los que dan una respuesta más alejada de la esperada son borrados y sólo quedan los más óptimos, que serán los padres de la siguiente generación, y así sucesivamente. Cada vez, los programas de generaciones sucesivas se acercan más y más a un resultado ideal, como consecuencia de este proceso de selección darwiniana. En el caso que nos interesa, un programa de ordenador escrito por John R. Koza, de la Universidad de Stanford, se vio enfrentado a datos reales de coordenadas celes-tes de planetas en distintas épocas. La respuesta que se le pedía era una fórmula matemática que los predijera correctamente. Por supuesto, la primera fórmula generada no tenía pies ni cabeza. La siguiente generación producía fórmulas que eran una modificación al azar de la del programa padre, por ejemplo un x2 en el programa progenitor podía ser un x3 en uno de los programas hijo, o un (x + 1)2 en otro. De todos los programas hijo, sólo sobrevivían los que predecían algo mejor las posiciones orbitales, y pasaban a ser padres de la generación siguiente. En apenas una cincuentena de generaciones, se llegó a obtener un programa de ordenador cuyo resultado era exactamente la tercera ley de Kepler, escrita además según el formalismo de Newton.
¿Qué podemos concluir de esto? Que si en nuestra especie hubiera habido una presión selectiva para predecir las posiciones planetarias, si a lo largo de generaciones nos hubiera ido literalmente la vida en ello, seguramente contaríamos en la actualidad con las leyes de Kepler implementadas en nuestro cerebro de forma innata, de igual manera que contamos con la capacidad de sumar y restar. En resumen, que tal vez las matemáticas alienígenas compartan con nosotros la aritmética de números enteros, pero poca cosa más. Una conclusión que recuerda lo que defienden los matemáticos finitistas, de que el único conocimiento matemático válido es el que se puede deducir a partir de los números enteros. El matemático alemán Leopold Kronecker, cabeza de este movimiento, llegó incluso a decir que «los números naturales son cosa de Dios. El resto, es un invento humano».
Nuestra exploración de las habilidades matemáticas de los animales parece justificar que una civilización capaz de desarrollar radiotelescopios deba tener algún tipo de matemáticas. Quizá distintas de las nuestras, pero matemáticas al fin y al cabo, por lo que resulta una buena opción basar un lenguaje de comunicación interestelar en ellas. De hecho, posiblemente sea la única opción.
Usando este enfoque se han realizado varios intentos, el más prometedor de los cuales es Lincos, acrónimo de la expresión latina lingua cosmica, un lenguaje de comunicación interestelar que fue creado en 1960 por el matemático alemán Hans Freudenthal, y publicado en su libro Lincos; design of a language for cosmic intercourse. Lincos es en realidad una expansión de otro «idioma cósmico» anterior llamado astraglossa, inventado en 1953 por el matemático británico Lancelot Hogben. Astraglossa era un lenguaje formal diseñado para enseñar matemáticas a los hipotéticos alienígenas. Lincos en cambio es un lenguaje más rico y potente, con el cual incluso se pueden comunicar conceptos no matemáticos complejos.
Los fonemas de Lincos son señales de radio (o radioglifos, siguiendo la nomenclatura de Hogben): distintos «pitidos» con diferentes significados, los cuales deben ser deducidos por el receptor. La estructura de Lincos está diseñada de tal manera que sea una lengua que se enseña a sí misma. Y como el movimiento se demuestra andando, ¿qué mejor que aprender a chapurrear un poco de Lincos por nosotros mismos? Así que desempolvemos nuestro radiotelescopio, sintonicémoslo en la frecuencia adecuada y conectémoslo a un reproductor de radio para poder escuchar las lecciones del curso «aprenda Lincos en diez minutos».
La primera lección que recibiríamos en nuestro receptor sería la siguiente:
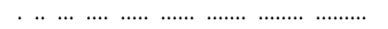
donde el símbolo · representa en realidad un «bip» elemental de radio, y los espacios en blanco, pausas. El tiempo avanzaría hacia la derecha, en el sentido de la lectura. Es decir, en nuestra radio esa señal sonaría como: bip, bipbip, bipbipbip, bipbipbipbip… Con poco esfuerzo, conseguiremos deducir que el contenido de la primera lección son los números naturales del 1 al 9. Es decir, esas señales «bip» representan números naturales, lo que por cierto se asemeja enormemente a la señal que Nicolas Tesla creía haber recibido de Marte.
Una vez entendemos esto, llega la segunda lección de Lincos. Suena así:
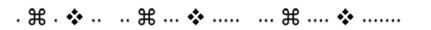
En esta ocasión, lo que hemos representado 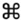por 
y por 
son dos nuevos tipos de pitidos de radio, que quizá suenen en nuestro receptor como «mooc» y «crack» respectivamente. Es decir, la primera frase de esta segunda lección de Lincos sería algo como «pip mooc pip crack pip pip». Para asegurar la comprensión de estas nuevas señales de radio, se hace necesario el envío de varios ejemplos, como se ha hecho aquí. Esta lección es un poco más difícil, pero merece la pena que el lector, antes de seguir leyendo, intente deducir el significado por sí mismo.
¿Lo ha conseguido? ¿Ha visto la relación? Si la intuición ha estado de su parte, habrá deducido que el radioglifo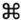 
representa la suma, o sea el signo +, y el radioglifo 
significa «igual a», es decir el signo =. Por tanto hemos aprendido ya dos nuevas palabras de Lincos. Pruebe ahora con la siguiente lección, e intente deducir el significado de otros dos nuevos radioglifos que aquí le presento. Tómese su tiempo:
¿Ya? Bien, partiendo de lo que ya hemos aprendido en la lección anterior, y usando simple lógica, se puede concluir fácilmente que estas dos nuevas «palabras» de Lincos, 
y 
, significan respectivamente los conceptos verdadero y falso (o correcto y erróneo). Una vez disponemos de estos dos conceptos, se puede enriquecer la conversación y resulta más fácil incluir nuevos conceptos, como en el ejemplo que sigue:
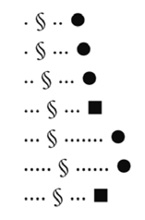
En este caso, contando con los conceptos de verdadero y falso, con un poco de esfuerzo, se puede deducir que el nuevo radioglifo § representa el concepto menor que. Terminaremos el curso con una última lección, en este caso puramente del campo de la lógica, introduciendo otras dos nuevas palabras de Lincos:
La solución, por supuesto, es que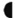 
y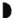 
representan respectivamente a las conjunciones y y o. Éste es el esquema propuesto por Freudenthal en su libro. Con sucesivas lecciones se introducen más definiciones, hasta que al final del libro se consigue un vocabulario tan completo que sirve para comunicar, no sólo conceptos matemáticos, sino cualquier tipo de información.
Sin embargo, el proceso es lento. Debido a que Freudenthal asume tan pocas cosas como punto de partida, es necesario comunicar un montón de información sobre el lenguaje y su funcionamiento antes de poder comenzar a comunicar información interesante. Para acelerar el proceso, el matemático Carl DeVito, junto al lingüista Richard Oehrle, pensaron en basar más el lenguaje en ciencia fundamental, a fin de dar un contexto en el que insertar las definiciones matemáticas de Lincos. Presentaron estas ideas en su artículo de 1990, «A language based on the fundamental facts of science». Asumieron como hechos científicos fundamentales que debería conocer cualquier civilización de constructores de radiotelescopios, saber contar, comprender los elementos químicos, conocer los puntos de fusión y ebullición de diferentes sustancias puras y las propiedades del estado gaseoso. Apoyándose en este presunto conocimiento común, es posible acelerar el proceso de aprendizaje del lenguaje y comunicar más pronto la información interesante. A partir de ello, desarrollaron su lenguaje de comunicación, una modificación de Lincos que me tomaré la licencia de llamar Lincos 2.0, dado que DeVito y Oehrle no bautizaron su lenguaje.
Otros trabajos en comunicación interestelar han surgido a raíz de Lincos. Mencionaré aquí los dos más interesantes. El primero es un concepto ciertamente novedoso, nacido de la capacidad computacional de los ordenadores. Se trata del envío de mensajes algorítmicos y lenguajes computables. La idea es mandar un algoritmo (un programa) cuya ejecución por parte de los receptores resulte en la enseñanza de conocimientos sobre nuestro mundo, y que les permita un nivel de interacción que sería imposible si la comunicación se basara únicamente en el intercambio de mensajes pasivos entre ellos y nosotros (dadas las distancias y tiempos que nos separan). Este es el caso del CosmicOS del ingeniero Paul Fitzpatrick del MIT. Por supuesto, este enfoque sumamente imaginativo asume, sin embargo, que la civilización receptora tiene que poseer capacidad computacional; para entender el mensaje, deben haber desarrollado algún equivalente a nuestros ordenadores, algo que nosotros tenemos desde hace sólo ocho décadas.
El otro es el desarrollo de «Lincos» visuales a la Arecibo, es decir, enviar imágenes por radio de una forma similar a la del mensaje de Arecibo, pero cuyo contenido sea una especie de lenguaje autodeducible como Lincos (solo que con caracteres escritos en lugar de radioglifos), que incluya también imágenes. Ésta es precisamente la opción que se eligió para la novela de Carl Sagan y posterior película Contact, donde dentro del mensaje de radio estaba encriptado, hoja tras hoja, todo un libro con símbolos, imágenes, diagramas y gráficos (las primeras lecciones tenían un asombroso parecido a las de nuestro curso de Lincos). Mensajes similares se han elaborado aquí y enviado ya a las estrellas. En 1999, se envió desde la antena de espacio profundo de Evpatoria (Ucrania) un mensaje, bautizado como Cosmic Call, dirigido a cuatro estrellas tipo Sol. El mensaje consistió en la emisión de 23 secuencias de radio, cada una de las cuales estaba formada por 16.129 pulsos. Todo el mensaje se transmitió tres veces a cada una de estas estrellas, durante un período de tres horas. En el 2003 se volvió a enviar el mismo mensaje (con pequeñas modificaciones) a otras cinco estrellas.
Al ver la curiosa cifra de 16.129, el lector atento inmediatamente se habrá preguntado si por medio anda algún número primo, y la respuesta en efecto es positiva. 16.129 es igual a 127 × 127, por tanto cada una de esas secuencias es en realidad una imagen cuadrada de 127 × 127 píxeles, es decir, una página del mensaje. Cuando estos pulsos se reordenan de forma similar a como se hizo con el mensaje de Arecibo, obtenemos páginas como éstas:
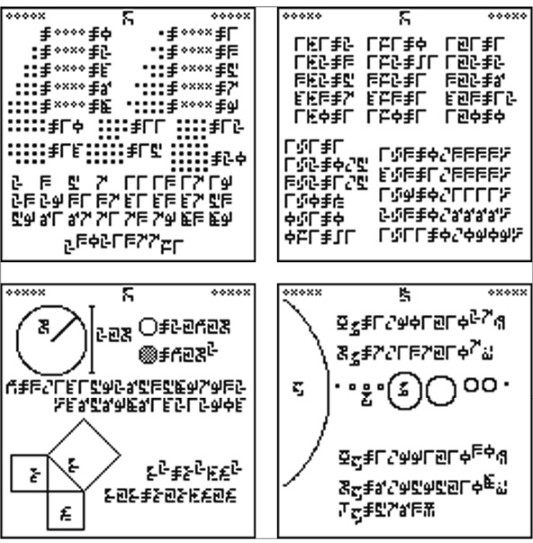
Páginas 1, 2, 5 y 11 del Cosmic Call de 1999. Cortesía de Yvan Dutil y Stephane Dumas.
Cada una de estas páginas se halla rodeada por un marco negro que aparece sólo si se ha decodificado correctamente. Como vemos, las primeras páginas son lecciones básicas de aritmética, y posteriormente se introducen conceptos más elaborados, como el teorema de Pitágoras o la forma del Sistema Solar. Por supuesto, los inconvenientes que tiene esta forma de enviar información son los mismos que tenía el mensaje de Arecibo: existen diferentes maneras de reordenar 16.129 elementos en una matriz 127 × 127; y atribuye además a los receptores del mensaje unas aptitudes visuales equivalentes a las nuestras.
Lincos, en cambio, no presupone ningún requisito sobre cómo percibe el mundo el receptor o sobre cuáles deben ser sus sentidos. Tan sólo que sean capaces de detectar ondas de radio con sus propios sensores, los cuales ya habrán diseñado ellos para sus sentidos. Tampoco existe ningún problema sobre cómo hay que ordenar los datos de la señal, pues su ordenación la da simplemente el orden temporal en que se reciben los diferentes radioglifos. Esta «universalidad» de Lincos frente a todos los demás medios de comunicación interestelar inventados predispone a los científicos a creer que si en alguna ocasión se recibe algún mensaje de nuestros vecinos galácticos, será algo análogo a Lincos.
Aun así, pese a ser un lenguaje lógico y fácilmente deducible, hay todavía una cuestión que destempla las espaldas a los que creemos factible la comunicación interestelar, y que enlaza con el tema con que abríamos este capítulo. Porque de nuevo topamos con que Lincos contiene una asunción implícita: a cada radioglifo se asocia un significado, algunos de ellos completamente abstractos; es por tanto un lenguaje simbólico. ¿Será Lincos entendible por una inteligencia que no tenga lenguaje simbólico? Aunque por otra parte ¿es posible una civilización tecnológica de seres inteligentes constructores de radiotelescopios y que no posean lenguaje simbólico?
En todo caso, aunque exista una incomprensión fundamental entre nuestra inteligencia y las inteligencias alienígenas, la mera detección de cualquier señal proveniente de una civilización extraterrestre, por indescifrable que fuera, será suficiente revulsivo para trastocar completamente nuestra sociedad y nuestra escala de valores, pues demostraría que no somos los únicos, que no somos la única posibilidad que tiene el Universo de conocerse a sí mismo, que hay alguien más.