Capítulo 9
Intermitencia relativa

El título del presente capítulo es más bien un concepto fractal que un dominio de aplicación. Volvemos, en efecto, a una aproximación que se ha hecho en varias de las aplicaciones. Al hablar de los errores a ráfagas, reprimíamos nuestra convicción de que entre dos errores el ruido subyacente se debilita, pero no cesa. Al discutir acerca de las distribuciones estelares, reprimíamos nuestro conocimiento de la existencia de una materia interestelar, que también puede ser que esté distribuida muy irregularmente. Y al hablar de las hojas de turbulencia, caíamos otra vez en el garlito, y tomábamos una imagen del régimen laminar en la que no pasa nada. Análogamente habríamos podido examinar la distribución de los minerales, sin introducir ninguna idea esencialmente nueva: las regiones en las que la concentración de oro o de cobre es suficientemente grande como para justificar la explotación minera están delimitadas por otras cuyo contenido en este metal se debilita, pero nunca llega a anularse. Ahora debemos llenar todos estos vacíos procurando no afectar demasiado las imágenes ya establecidas. Esbozaré ahora una manera de hacerlo, que va bien cuando el objeto y las intermisiones son de la misma naturaleza y sólo difieren en la intensidad. Para ello, me dejaré inspirar una vez más por las viejas matemáticas puras, calificadas de «inaplicables». Este capítulo será relativamente técnico y seco.

Definición de los dos grados de intermitencia

Por necesidades de contraste, nos conviene caracterizar los fenómenos que hemos considerado hasta ahora como «absolutamente intermitentes». El epíteto está motivado por el hecho de que en las intermitencias no pasa absolutamente nada: no hay energía de ruido, ni materia, ni disipación turbulenta. Además, todo lo que «ocurre» en un intervalo, un cuadrado o un cubo, se concentra por entero en una pequeña porción, que a su vez está contenida en un subconjunto al que llamamos «simple», esto es, un conjunto formado por un número finito de subintervalos, subcuadrados o subcubos, cuyas longitud, área o volumen total, se pueden hacer tan pequeños como se quiera. Yendo aún más lejos, diremos que la intermitencia es «degenerada» si todo ocurre en un solo punto. Por contraste, diremos que la intermitencia es «relativa» si no hay ningún conjunto simple en el que no pase nada, mientras que existe un conjunto simple en el que está contenido casi todo lo que pasa.

Medida fractal de Besicovitch

Permanezcamos dentro del contexto triádico original de Cantor, en el cual se divide [0,1] en tercios, éstos a su vez en tercios y así sucesivamente, y partamos de una masa distribuida sobre [0,1] con densidad uniforme e igual a 1. Borrar el tercio central divide esta masa en tres partes iguales a 1/2, 0 y 1/2, repartidas con densidades de 3/2, 0 y 3/2. Esto se generaliza fácilmente suponiendo que cada etapa divide la masa inicial en partes iguales, respectivamente, a p₁, p₂ y p₃, repartidas según las densidades 3p₁, 3p₂, y 3p₃ (satisfaciéndose, claro está, que 0 ≤ p_m < 1 y p₁ + p₂ + p₃ = 1). Cuando se haya repetido este procedimiento infinitas veces, la masa formará lo que llamaremos una medida de Besicovitch. ¿Qué podemos decir de ella? Para empezar, está claro que ningún intervalo abierto constituye una intermisión absoluta. En efecto, una tal intermisión tendría que incluir por lo menos un intervalo de longitud 3^−k, cuyas extremidades fueran múltiplos de 3^−k, y sabemos que cualquier intervalo de esta forma contiene una masa no nula. Sin embargo, cuando k es grande, dicha masa se hace sumamente pequeña, pues Besicovitch ha demostrado (aquí simplificamos su resultado) que casi toda la masa se concentra en 3^kD intervalos de longitud 3^−k, en los que se tiene:

D = −∑p_mlog₃p_m < 1

Cuando k aumenta, el porcentaje de intervalos no vacíos tiende a cero, mientras que la longitud total de éstos es aproximadamente igual a 3^k(D−1), y por lo tanto tiende también a cero. Cuando p₁ → 1/2, p₂ → 0, p₃ → 1/2, el conjunto de Besicovitch tiende hacia un polvo de Cantor; es fácil verificar que D tiende hacia la dimensión log 2/log 3 de este último conjunto.

Si en vez de dividir [0,1] en tercios, se divide en décimos, se obtiene el conjunto de los números reales entre 0 y 1 para los que las distintas cifras tienen las probabilidades p_m. Obsérvese que, formalmente, D es una «entropía» en el sentido de la termodinámica, o también una «información» en el sentido de Shannon (véase Billingsley 1965). Y lo que es más importante, D es una dimensión de Hausdorff-Besicovitch. Sin embargo, el conjunto de Besicovitch es abierto, mientras que todos los conjuntos estudiados anteriormente eran cerrados (la diferencia está relacionada con el contraste entre las intermitencias absoluta y relativa). Al generalizar la dimensión a conjuntos abiertos, se pierden muchas de sus propiedades, ¡entre las que hay algunas que tienen un interés práctico directo, y a las que habíamos empezado a acostumbramos! Por ejemplo, el exponente de homotecia del conjunto de Besicovitch no es D sino 1; sin embargo, el conjunto de los 3^kD segmentos en los que se concentra la masa es completamente homotético con exponente D.

Examinemos ahora el problema del condicionamiento, una vez se ha llevado a cabo la construcción de Besicovitch a lo largo de un número de etapas K, finito pero grande. Para ello, elijamos un «intervalo de prueba» al azar, de longitud 3^−k, donde k es menor que K; en casi todos los casos, este intervalo caerá fuera del conjunto en el que está concentrada casi toda la masa. Con respecto a la densidad media en [0,1], que ya sabemos que es igual a 1, la densidad en casi cualquier intervalo de prueba será casi despreciable. Su distribución será independiente del intervalo por el hecho de ser degenerada. Pero dividamos la densidad en el intervalo de prueba por su propia media. Encontraremos que la distribución de probabilidad de este cociente será también la misma en todas partes, y, además no degenerada. Todo ello está ilustrado en la Figura 151.

Caos multiplicativo: generalización aleatoria de la medida fractal de Besicovitch

Por muy sugerente que sea la construcción del párrafo anterior, aún hay que randonizarla. Se me han ocurrido varios métodos para hacer esto, a partir de unos trabajos de Kolmogorov, Obukhov y Yaglom (importantes, a pesar de algunos errores y ciertos aspectos discutibles). Para esbozar estos métodos, trabajemos en dos dimensiones y en división triádica. Cada nivel parte de una celdilla formada por nueve subceldillas, con una densidad inicial uniforme; después, las densidades correspondientes a las nueve subceldillas se multiplican por factores aleatorios, que siguen todos la misma distribución. La construcción varía según el grado de aleatoriedad que se desee. El caso mínimo consiste en fijar de antemano los valores de estos factores, dejando sólo al azar la distribución de los mismos entre las celdillas. En el caos multiplicativo de Mandelbrot 1974d,f, se eligen al azar los factores multiplicativos, independientemente unos de otros.

El caos multiplicativo de Mandelbrot 1972j va más allá, y es el propio proceso el que engendra la cascada.

P.S. Los caos multiplicativos y las medidas fractales introducidos en Mandelbrot 1972j, 1974d,f se hallan en vías de devenir muy importantes. El término que parece prevalecer es el de «medida multifractal».

LÁMINA 151. Escaleras diabólicas de Besicovitch

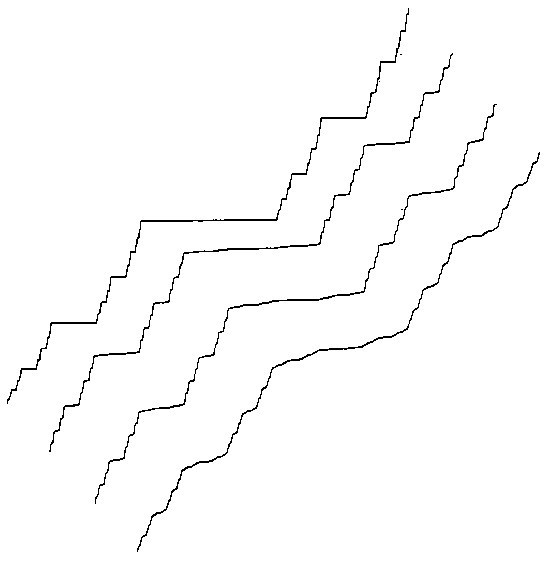
FIGURA 151

Bajo una escalera del diablo (véase la Figura 73), se ven tres escaleras de Besicovitch, cuya construcción se ha descrito en la pág. 148; aquí p₁ = p₃. Su característica más chocante, al compararla con la escalera del diablo, se puede observar si se divide la abscisa en un gran número de segmentitos. Ninguno corresponde a una marcha horizontal; sin embargo, una proporción muy grande del desplazamiento vertical tiene lugar en un desplazamiento horizontal muy pequeño, cuya dimensión fractal aumenta a medida que uno se aleja de la escalera de Cantor.