Volvamos ahora nuestra atención a otro gran problema clásico, muy vasto y mal explorado, del que sólo abordaremos los aspectos que hagan intervenir los objetos fractales y la noción de dimensión. Aun desde este punto de vista, el desarrollo no tendrá la amplitud que merece su importancia práctica y conceptual; nos limitaremos a algunas cuestiones que tienen el mérito de introducir temas nuevos de interés general, siendo el propio tema tratado en concreto en Mandelbrot 1967b, 1967k, 1972j, 1974d, 1974f, 1975f, 1976c, 1976o, y 1977b.

El estudio de la turbulencia tiene claramente cabida en un ensayo dedicado hasta el momento a la forma de la superficie terrestre, a la distribución de los errores extraños y a la de los objetos celestes. Ya desde 1950, von Weizsäcker y otros físicos habían barajado la posibilidad de explicar la génesis de las galaxias por un fenómeno turbulento a escala cósmica; sin embargo, la idea no pudo arraigar. Si vale la pena volver a pensar en ella en serio, es porque el estudio de las galaxias ha progresado, porque la teoría de la turbulencia se está metamorfoseando, y porque estoy en condiciones de proporcionar la base geométrica fractal que le hacía falta. Los trabajos de 1950 se referían, efectivamente, a la turbulencia homogénea, tal como fue descrita por Kolmogorov, Obukhov, Onsager y Weizsäcker, entre 1940 y 1948.

Era necesaria una audacia extrema para pretender explicar así un fenómeno sumamente intermitente —como las galaxias— mediante un mecanismo de turbulencia homogénea. Lo que ha variado desde entonces es que se ha reconocido universalmente que la turbulencia homogénea es una quimera, una aproximación cuya utilidad es menor de lo que se había pensado en un principio. Hoy se reconoce que una de las características de la turbulencia reside en su carácter violentamente «intermitente». Como todo el mundo sabe, el viento no sólo sopla siempre a ráfagas, sino que lo mismo ocurre a otras escalas. Así pues, he reanudado el esfuerzo unificador de von Weizsäcker buscando una relación entre dos intermitencias. La herramienta que propongo son, claro está, las fractales.

Su utilización para abordar la geometría de la turbulencia es inédita, pero es natural desde el punto de vista histórico, sobre todo si se tiene en cuenta el nexo entre los conceptos de fractal y de homotecia interna. En efecto, una variante algo vaga de la homotecia había sido concebida, precisamente con motivo de una teoría de la turbulencia, ni más ni menos que por nuestro Lewis Fry Richardson. Y una forma analítica de homotecia ha tenido sus primeros éxitos en la aplicación a la turbulencia de la mano de Kolmogorov y de Obukhov y Onsager. Como todo fluir viscoso, la corriente turbulenta en un fluido está caracterizada por una medida intrínseca de escala, el número de Reynolds, y los problemas de intermitencia son especialmente agudos cuando dicho número es muy grande, como ocurre sobre todo en los casos del océano y la atmósfera.

Sin embargo, el problema de la estructura geométrica del soporte de la turbulencia no se ha planteado hasta muy recientemente. En efecto, la imagen que uno se hace de este fenómeno sigue en general «congelada» en los términos en los que fue descrito por vez primera, hará unos cien años, por Boussinesq y Reynolds. El modelo consistió durante todo este tiempo en el flujo dentro de un tubo: cuando la presión corriente arriba es suficientemente débil, todo es regular y «laminar», cuando la presión es suficientemente grande, todo se hace, muy rápidamente, irregular y turbulento. En este caso prototípico, el soporte de la turbulencia es, por consiguiente, o «vacío», en el sentido de inexistente, o bien llena el tubo por completo, y ni en uno ni en otro caso hay razones para plantearse dudas al respecto. En un segundo caso, el de la estela que deja tras de sí un barco, por ejemplo, las cosas se complican: entre la estela, que es turbulenta, y el mar ambiente, que se supone laminar, hay una frontera; pero, aunque ésta sea muy irregular, es tan clara, que normalmente no parece razonable estudiarla independientemente, ni tampoco verdaderamente necesario tratar de definir la turbulencia mediante un criterio «objetivo». En un tercer caso, el de la turbulencia plenamente desarrollada en los fuelles de un órgano, las cosas son más sencillas aún, puesto que toda estructura de este tipo ya parece de por sí turbulenta —concepto siempre mal definido también—. Sin embargo, la manera de llegar a ello es un tanto curiosa (si hay que creer algunas leyendas tenaces). Se dice (espero que sólo sean murmuraciones) que cualquier fuelle de órgano es, por principio, inadecuado para el estudio de la turbulencia; espontáneamente, en vez de llenar todo el volumen que se le ofrece, la propia turbulencia parece «turbulenta», presentándose en bocanadas irregulares; sólo gracias a esfuerzos de redisposición gradual, se llega a estabilizar el conjunto, a la manera del tubo de Boussinesq-Reynolds.

Por este motivo, y sin poner en cuestión la importancia práctica de los tubos, soy de los que no se quedan tranquilos. ¿Es la «turbulencia de laboratorio» típica de la «turbulencia natural», y el fenómeno «turbulencia» es único? (aun sin tener en cuenta sus dos aspectos verdaderamente distintos, a saber, turbulento por oposición a laminar, y turbulento-disipativo en contraste con turbulento no disipativo). Para saberlo, habría que definir primero los términos, trabajo que parece como si nadie quisiera afrontar.

Propongo que se aborde esta definición indirectamente, invirtiendo el procedimiento habitual: partiendo de un concepto mal especificado de lo que es turbulento, intentaré primero establecer que la turbulencia natural muy avanzada, o su disipación, están «concentradas en», o «sostenidas por», conjuntos espaciales cuya dimensión es una fracción, del orden de magnitud D = 2,5. A renglón seguido, me aventuraré a proponer que se defina como turbulento a todo flujo cuyo soporte tenga una dimensión comprendida entre 2 y 3.

Las corrientes en el seno de los fluidos son fenómenos multidimensionales, donde las tres componentes de la velocidad son funciones dé las tres coordenadas espaciales y del tiempo, pero el estudio empírico ha de pasar, por el momento, por uno o varios «cortes» unidimensionales, constituyendo cada una de éstos la crónica de una de las componentes de la velocidad en un punto fijo. Para hacemos una idea intuitiva de la estructura del corte para una masa atmosférica desplazándose ante el instrumento, invirtamos los papeles y tomemos como «instrumento» un avión. Un avión muy grande sirve para ilustrar un nivel muy grosero del análisis; algunos rincones de la atmósfera parecen turbulentos con toda evidencia, y en ellos el avión es sacudido; en contraste, el resto parece laminar. Pero repitamos la prueba con un avión más pequeño: por una parte, éste «siente» arranques turbulentos allí donde el grande no los había sentido, y por otra, descompone cada sacudida del mayor en una ráfaga de sacudidas más débiles. Así pues, si un pedazo turbulento del corte se examina en detalle, puede observarse que presenta inserciones laminares, y así sucesivamente a medida que el análisis se va refinando.

Hablando de la configuración espacial, von Neumann 1949 observa que la turbulencia se concentra sin lugar a dudas «en un número asintóticamente creciente de choques cada vez más débiles». En nuestros cortes unidimensionales, cada choque aparecerá como un punto. Las distancias entre choques están limitadas por una escala interna no nula η, que depende de la viscosidad, pero que, a fin de facilitar la conceptualización, conviene imaginar como η = 0. Propongo que se añada a esto la idea de que los choques están infinitamente hojaldrados. De este modo se manifiesta, en nuestros cortes unidimensionales, el tipo de estructura cantoriana con la que ya nos hemos familiarizado, desde que apareció en el Capítulo 4 al tratar de los errores extraños. La diferencia estriba en lo siguiente: en los intervalos entre errores no había nada, mientras que en las intermisiones laminares, el flujo no se detiene, sino que simplemente se vuelve más regular que en otros lugares. Pero resulta evidente que hasta esta diferencia desaparecería si se considerara, además de los errores, el ruido físico que los produce. Esto sugiere que para construir un modelo de la turbulencia o del ruido hay que proceder por dos aproximaciones sucesivas. La primera supondrá que el flujo laminar es tan regular que es prácticamente uniforme, y por lo tanto despreciable, conduciéndonos de este modo al esquema cantoriano de dimensión menor que 3; la segunda aproximación supondrá que cualquier cubo del espacio contiene por lo menos algo de turbulencia. En estas condiciones, si no se tiene en cuenta la turbulencia allí donde su intensidad sea muy débil, uno espera reencontrar, poco más o menos, la primera aproximación. Remitamos pues esta segunda aproximación al Capítulo 9 y ocupémonos aquí de la primera.

Parece razonable exigir que las intersecciones del conjunto de turbulencia con una recta cualquiera tengan la estructura cantoriana que tenía el conjunto empleado para representar los errores extraños. Hemos de idear, pues, conjuntos que tengan intersecciones como ésas.

El estudio de la intermitencia de la turbulencia fue estimulado por Kolmogorov 1962 y Obukhov 1962, pero el primer modelo explícito fue el de Novikov y Stewart 1964. Dicho modelo descubre otra vez, independientemente, el principio de las cascadas de Fournier y de Hoyle, y, por lo tanto, vuelve a descubrir —sin saberlo— el camino trazado por Cantor. Si lo hubieran sabido, quizá nuestros autores se hubieran llevado un buen susto. Afortunadamente, yo me he dado cuenta de ello, y eso me ha llevado a desarrollos muy prometedores.

La idea es que el soporte de la turbulencia es engendrado por una cascada, de la que cada etapa parte de un remolino y da como resultado N sub-remolinos de un tamaño r veces menor, en cuyo seno se concentra la disipación. Está claro con ello que D = log N/log(1/r).

Esta dimensión D puede estimarse empíricamente, pero hasta hoy nadie ha afirmado seriamente haberla deducido de consideraciones físicas fundamentales. Al contrario, en el caso de la astronomía, Fournier y Hoyle encuentran razones para esperar que D = 1. Se sabe (págs. 100-101) que esto contradice el resultado empírico, pero parece que incluso una teoría falsa puede ser psicológicamente tranquilizadora.

Segunda novedad: en astronomía, D < 2, pero en turbulencia se ha de suponer N mucho mayor que 1/r, y la dimensión es de aproximadamente 2,5. De hecho, uno de los triunfos de las visiones fractales del universo y de la turbulencia habrá consistido en demostrar la necesidad de D < 2 en el primer caso, y D > 2 en el segundo, a partir del mismo hecho geométrico. En efecto, para evitar lo que se llamó «el cielo en llamas», en el Capítulo 6 era necesario que, al dirigir la mirada al azar, no se encontrara, con seguridad casi absoluta, ninguna fuente de luz, lo que implicaba que D < 2. Por el contrario, a fin de explicar el hecho de que la turbulencia está muy esparcida, es necesario en este caso que un corte hecho al azar tenga una probabilidad no nula de intersecar el soporte de la turbulencia, lo que implica que D > 2.

Comportamiento de la dimensión fractal frente a las intersecciones. Construcción de Cantor a varias dimensiones

La cascada de Novikov y Stewart es importante, pero conviene dar un paso atrás, como ya hemos hecho varias veces, y estudiar en detalle algunas construcciones no aleatorias cuya regularidad es excesiva, y en las que hay un punto central que juega un papel demasiado especial. La generalización de la construcción de Cantor se puede hacer de varias maneras, que conducen a resultados muy distintos. Tenemos un ejemplo en la «esponja fractal de Sierpinski-Menger» ilustrado en la Figura 145. En un segundo ejemplo, el mordisco con que se empieza el proceso es el veintisieteavo central, definido como un cubito concéntrico con el primero y de lado 1/3. A continuación se hace lo mismo con cada uno de los 26 cubitos que quedan, luego con los sub-cubos restantes, etc.

Lo que queda, si se sigue la construcción indefinidamente, es una especie de pedazo de Emmenthal evanescente. Se puede imaginar la forma que tendrían sus lonchas a partir de las que hemos entrevisto cuando describíamos el conjunto que quedaba fuera de los cráteres de la Luna, visto según la óptica de un pintor cubista. El volumen del objeto es nulo y está lleno de agujeros cuadrados de todos los tamaños, separados por tabiques infinitamente hojaldrados. Se comprueba fácilmente que tiene homotecia interna, y que su dimensión es igual a log 26/log 3. Podemos proponer una generalización inmediata: en lugar de sacar cada vez el veintisieteavo central, podemos sacar el cubo central de arista 1 − 2r; la dimensión se convierte entonces en

cuyo valor siempre es mayor que 2, pero se acerca más a este valor cuanto mayor es 1/r. La desigualdad D − 2 > 0 concuerda con la intuición de que nuestras «pastelerías» fractales son «más gruesas» que cualquier superficie ordinaria de dimensión 2.

Según un tercer método y en el caso triádico, los mordiscos son mayores. El primero de ellos deja en las esquinas del cubo inicial 8 cubitos de lado 1/3, continuándose la construcción de manera natural. Al final se tiene también un polvo de puntos inconexos. Sin embargo, la dimensión es igual a log 8/ log 3, que es menor que dos y mayor que uno. Desde el punto de vista geométrico, el polvo que se obtiene de esta manera es, sencillamente, el producto de tres polvos triádicos de Cantor unidimensionales (exactamente igual que un cuadrado es el producto de sus lados). Cambiemos ahora el método, de manera que los 8 cubitos que se dejan en cada etapa tengan una arista de longitud arbitraria r, con la única condición de que sea menor que 1/2. Al final se tiene siempre un polvo de puntos de dimensión idéntica a log 8/log(1/r), cantidad que es arbitraria, salvo en la limitación de que ha de ser menor que 3. Concuerda con la intuición el hecho de que un conjunto más rico que un polvo tenga una dimensión mayor que 0, pero es contrario a ella que un conjunto «menos conexo» que una línea tenga una dimensión mayor que 1. Pero este resultado no hace más que confirmar lo que ya sabemos desde que hemos estudiado los objetos celestes (construcción de Fournier-Charlier), a saber, que no hay ninguna relación entre conectividad y dimensión fraccionaria. Observemos no obstante, que, para obtener un polvo de dimensión mayor que 1, hemos recurrido a mordiscos cuya forma es sumamente especial. En ausencia de una ligadura geométrica como la que teníamos en el caso anterior, por ejemplo en el caso de construcciones regidas por el azar, es de esperar que se puedan entrever relaciones entre la dimensión y la conectividad. El problema queda pendiente.

Recordemos que también el universo de Fournier-Charlier puede ser considerado como una variante espacial de la construcción de Cantor.

La primera motivación para introducir formas estadísticas del polvo de Cantor está relacionada, como en los capítulos precedentes, con la búsqueda de un modelo más irregular, con la esperanza de que sus propiedades sean más realistas. Una nueva motivación procede del deseo de encontrar la relación entre conectividad y dimensión, uno de cuyos aspectos hemos discutido en la sección anterior. Sin más ambages, consideremos mordiscos completamente aleatorios y tridimensionales, generalizando de este modo el método que hemos empleado ya a propósito de los errores extraños y los cráteres circulares de la Luna. Lo más natural es determinar que los mordiscos sean bolas abiertas, esto es, interiores de esferas, siendo el valor esperado para el número de mordiscos con volumen superior a u igual a K(3 − D)/u³. La forma K(3 − D) para la constante del numerador se ha elegido de tal manera que el criterio buscado dependa de D: cuando la constante sea mayor que 3K, el conjunto que queda es casi con toda seguridad vacío (y D, que es negativo, no es una dimensión), mientras que para D > 0, el conjunto residual tiene una probabilidad no nula de ser no vacío, y en este caso, tiene una forma de homotecia interna de dimensión D. En particular, el volumen del conjunto que queda es siempre nulo; más concretamente, es casi seguro que una esfera de radio R, cuyo centro se haya escogido al azar, no interesectará al conjunto residual. Por consiguiente, es necesario tomar precauciones para evitar esta degeneración (¡no hay que olvidar la forma condicional del principio cosmográfico!); sabemos que una buena manera de hacerlo consiste en estudiar la geometría de este conjunto a partir de un origen que forme también parte del mismo.

He aquí lo que se obtiene: cuando D está cerca de 3, los mordiscos dejan un conjunto formado por «velos infinitamente hojaldrados». Sus intersecciones con planos o con superficies esféricas tienen la forma de filamentos infinitamente bifurcados como los que encontrábamos sobre la Luna, nuestras «lonchas de Emmenthal». Sus intersecciones con rectas, o con círculos (excepto por algunos detalles), son «ráfagas de errores extraños». Para los D menores, se tienen «hilos infinitamente ramificados», pero esta vez en el espacio y no en el plano. Por lo tanto, sus intersecciones con planos o con esferas son polvos de puntos, y sus intersecciones con rectas o círculos son, casi con toda seguridad, vacías. Cuando D es pequeño, todo el conjunto residual es un polvo; sus intersecciones con los planos y las rectas son, casi con toda seguridad, vacías.

P.S. Mordiscos espaciales y modelos de la distribución de las galaxias. El concepto de «lagunosidad de una fractal».

La Figura 111 señala que mi primer modelo de la distribución de las galaxias da lugar a grandes vacíos y regueros, y observa que esto estaría muy bien, pero sólo con la condición de que la intensidad de estos rasgos pueda ser atenuada. Con este fin, sólo he tenido que pasar lista a los polvos descritos en el párrafo anterior. Luego, eligiendo mordiscos cuya forma no es esférica, he identificado una nueva característica de las fractales, que he denominado «lagunosidad», y que es esencial desde entonces —por ejemplo en física. Véanse los capítulos 34 y 35 de Fractal Geometry of Nature.

Con todo, sigue siendo cierto que no puede haber una fractal sin grandes vacíos. Por esta razón, todos aquellos que creen en las fractales se han alegrado del descubrimiento bien conocido, a finales de 1982, de vacíos intergalácticos de tamaño «absolutamente imprevisto».

¿Son fractales las singularidades de la ecuación de Navier- Stokes? ¿Permitirá esto resolverlas por fin?

No se ha podido establecer aún ninguna relación lógica entre la teoría de la turbulencia homogénea de Kolmogorov y las ecuaciones de Navier-Stokes, que, según se cree, gobiernan el flujo de los fluidos, incluso cuando éste es turbulento. Ésta es, sin duda, la razón que explica por qué —entre los hidrodinamistas— la validación de las previsiones de Kolmogorov ha sido más bien fuente de malestar que de alegría. Se habría podido temer que la introducción de mi noción de homogeneidad fractal acentuara este divorcio, pero estoy convencido de que va a pasar lo contrario. Éstas son mis razones: se sabe que, muy a menudo, la física matemática consigue desbrozar un problema reemplazando sus soluciones por el esqueleto formado por sus singularidades; pero ése no ha sido el caso para las soluciones turbulentas de las ecuaciones de Navier, incluso después de Kolmogorov, y en mi opinión eso es lo que más ha contribuido a retrasar el estudio. Pienso que —gracias a unas características específicas de los objetos fractales, que no podemos detenemos a describir aquí—, por lo que se refiere a la naturaleza de dichas singularidades, esta laguna está muy cerca de ser llenada.

P.S. Precisé estas ideas en 1976c, formulando la conjetura de que las singularidades de las ecuaciones de Navier-Stokes y de Euler son fractales. Esta conjetura parece estar en camino de confirmarse, como se dice en el Capítulo 11 de Fractal Geometry of Nature

LÁMINA 145. Un queso en el espacio tridimensional: la esponja de Sierpinski-Menger

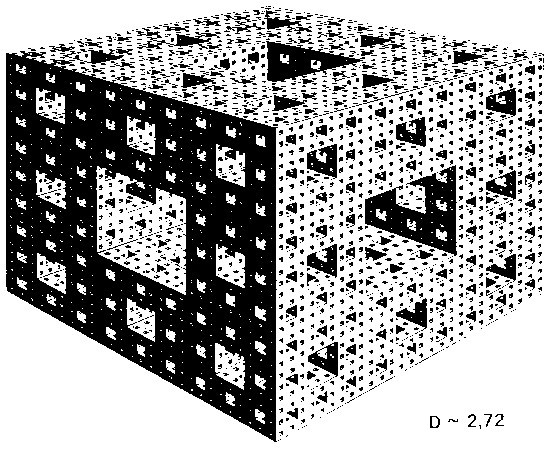
FIGURA 145

El principio del proceso de construcción es evidente. Si se aplica indefinidamente, se obtiene un objeto geométrico, conocido como esponja de Sierpinski-Menger, tal que cada una de sus caras exteriores, conocido como tapiz de Sierpinski, es una figura de área nula, mientras que el perímetro total de los agujeros es infinito. Obsérvese que las intersecciones del límite, con las medianas o con las diagonales del cubo inicial, son todas ellas conjuntos triádicos de Cantor. (Figura reproducida con la autorización del editor de «Studies in Geometry» de L. M. Blumenthal y K. Menger, © 1970 by W. H. Freeman and Co.).

Capítulo 8 La geometría de la turbulencia

Capítulo 8
La geometría de la turbulencia