Ahora que ya conocemos mejor el movimiento browniano ordinario, vamos a pasar a los vagabundeos sin bucles, a los que les está prohibido —por definición— pasar más de una vez por un mismo punto. Nos servirán de transición hacia las curvas brownianas fraccionarias, que simplemente tienen una tendencia a no volver atrás. Examinaremos finalmente las superficies brownianas, primero las ordinarias y después las fraccionarias, que nos proporcionarán un modelo de todo el relieve terrestre, y nos permitirán representar las costas.

Para empezar, dado un enrejado de puntos, en el plano o en el espacio (por ejemplo, aquéllos cuyas coordenadas son todas enteros), consideremos el vagabundeo que pasa de uno de estos puntos hacia uno de sus vecinos escogido al azar, de manera que aquéllos que no han sido visitados aún tienen la misma probabilidad de serlo en el instante siguiente, y los otros tienen probabilidad nula (están excluidos). En el caso degenerado de la recta, este vagabundeo continúa indefinidamente en una u otra dirección sin invertirse jamás. Pero en los casos no degenerados del plano o el espacio, el problema es muy interesante y muy difícil. Su importancia práctica en el estudio de los polímeros es, sin embargo, tan grande, que ha sido objeto de simulaciones muy detalladas.

El resultado que nos interesa es el siguiente, debido a Domb 1964-65 y descrito por Barber & Ninham 1970. Después de n pasos, la media cuadrática del desplazamiento R_n es del orden de magnitud de n elevado a la potencia 2/D. Esto sugiere claramente que en un círculo o una esfera de radio R alrededor de un sitio, debe esperarse encontrar aproximadamente R^D sitios más. ¡Qué tentador es sacar la conclusión de que este D es una dimensión! Sus valores son los siguientes: para la recta, D = 1; para el plano, D = 4/3; para el espacio ordinario, D = 5/3; y por fin, en un hiperespacio cuya dimensión tienda hacia infinito, el riesgo de que se forme un bucle disminuye y D − 2.

Parece una coincidencia que el D = 4/3 correspondiente al plano represente los datos de Richardson para las costas más accidentadas. De todas formas no hay por qué insistir más en ello, pues, en el caso de vagabundeos sin bucles, el principio cosmográfico, sobre cuya importancia ya hemos insistido bastante, no parece ser aplicable bajo ninguna de sus formas.

Comparemos, sin embargo, el comportamiento de M(R) para un vuelo de Lévy y para un vagabundeo sin bucles. La forma analítica es la misma, pero las razones en las que se basa son sumamente diferentes. En efecto, el vuelo de Lévy procede por saltos independientes, y D < 2 se debe a la presencia ocasional de valores muy grandes separando los distintos racimos. En un paseo aleatorio sin bucles los saltos tienen una longitud fija, y D < 2 se debe a que, por el mismo hecho de evitar las posiciones ocupadas con anterioridad, el movimiento adquiere una especie de persistencia.

Mi texto inédito acerca de las Formes Nouvelles du hasard dans les Sciences (retomado en parte en Mandelbrot y Wallis 1968 y en Mandelbrot 1973), bautiza estas causas con los nombres de Efecto de Noé y Efecto de José, respectivamente, honrando así a dos héroes bíblicos, el del Diluvio y el de las siete vacas gordas y las siete vacas flacas, respectivamente.

Vale la pena tomar en serio la historia bíblica de José. No cabe duda de que se refiere a un acontecimiento real, esto es, a una serie de crecidas y estiajes del Nilo, pues los niveles del Nilo son extraordinariamente persistentes, y lo mismo ocurre con muchos otros ríos. Hay que señalar este fenómeno porque vamos a utilizar largamente la descripción matemática que he dado de él en Mandelbrot 1965h y, con más detalles e ilustraciones, en Mandelbrot y Wallis 1968. Consiste en representar las riadas anuales del Nilo mediante los crecimientos de un cierto proceso estocástico, que se obtiene modificando el movimiento browniano escalar de la Figura 71, para suavizarlo y hacerlo menos irregular a cualquier escala. La intensidad del alisado, y por ende la de la persistencia de los crecimientos, depende de un solo parámetro; para el proceso correspondiente al valor H de este parámetro he propuesto el nombre de movimiento browniano fraccionario, que se denotará por B_H(t). Por convenio, el valor H = 0,5 corresponde al caso clásico, en el que no hay ninguna dependencia, mientras que la persistencia aumenta progresivamente a medida que H crece de 0,5 a 1. Así pues, las riadas anuales del Nilo, que están muy lejos de ser independientes, pueden ser representadas por los crecimientos anuales de un movimiento browniano fraccionario de parámetro H = 0,9. Para el Loira, H está más cerca de 0,5; para el Rhin, H = 0,5, salvo errores.

Todo esto es apasionante, pero no constituye más que una preparación para el estudio de las curvas en el plano. Allí también, es razonable tratar de generalizar el movimiento browniano de modo que su dirección tienda a persistir, sin perder su carácter de curva continua. (El Capítulo 6, muy al contrario, trata de romper la continuidad sin introducir la persistencia). Esto equivale a buscar, no la obligación, sino simplemente la tendencia, más o menos intensa, a que la trayectoria evite intersecarse a sí misma. Si se quiere, además, conservar la homotecia interna —como ya es regla en el presente Ensayo— lo más sencillo será que las dos coordenadas estén sometidas a movimientos brownianos fraccionarios, estadísticamente independientes y con el mismo parámetro H.

Las Figuras 124 a 126 representan tres ejemplos de curvas obtenidas de esta manera. Si hubiéramos dibujado cada una de las coordenadas en función del tiempo, su forma habría diferido poco de la de la Figura 57, mientras que en dos dimensiones el efecto de la elección de H es incomparablemente más acentuado. Para el primer trazado (Figura 124) H toma el valor 0,9, que ya hemos dicho que explica el Efecto José para el Nilo. Al tener así una tendencia muy fuerte a continuar en cualquier dirección en la que se haya metido, se ve claramente cómo nuestro punto se difunde mucho más rápidamente de lo que lo haría con un movimiento browniano normal; por ello, consigue evitar los bucles muy visibles. Hasta tal punto que —volviendo a una cuestión discutida en el Capítulo 2— nuestra curva daría a priori una imagen muy razonable de la forma de las costas menos irregulares.

Esto lo confirma además el valor de la dimensión fractal: la D del movimiento browniano fraccionario plano es 1/H. Con ello resulta ser mayor o igual que 1 —como ha de ser, intuitivamente, para una curva continua—. Además, el caso llamado «persistente» con H > 1/2 da una D inferior a 2, lo que intuitivamente concuerda también con el hecho de que dicha curva recubre el plano de una manera menos densa que el movimiento browniano ordinario. Así pues, en el caso específico de la Figura 124, se tiene D = 1/0,9 = 1,11. Para trazar las Figuras 125 y 126, se ha cambiado H, conservando la semilla de generador pseudoaleatorio ya utilizada en la Figura 124. Este procedimiento subraya el aumento progresivo de la irregularidad, que es consecuencia de la disminución de H; se ve también cómo la tendencia a evitar los bucles se debilita a medida que D aumenta. Por consiguiente, nuestra búsqueda de un modelo de costas no ha terminado aún; la reanudaremos dentro de unos instantes.

Señalemos que el movimiento browniano fraccionario escalar puede definirse también para 0 < H < 0,5, pero una curva cuyas dos coordenadas son tales funciones se difunde más lentamente que el movimiento browniano usual, volviendo constantemente sobre lo andado, y cubriendo el plano repetidas veces. Como en el caso H = 0,5, la dimensión fractal toma el mayor valor concebible en el plano, esto es, D = 2.

Veamos dónde estamos: hemos fracasado ya un par de veces en la búsqueda de un atajo que nos permitiera representar una costa sin preocuparnos por el relieve. Ya es hora de darse cuenta de que esta esperanza no era razonable, y de atacar el problema de las costas junto con el de todo el relieve en su conjunto. Dentro de poco construiremos un modelo que genera superficies estadísticamente idénticas a la representada en la Figura 128, pero tenemos que dar antes un último rodeo.

Como sabemos de sobra las dificultades que plantean los bucles, abordaremos el problema del relieve a través de unas curvas características, que no puedan tener ninguno. Si no tenemos en cuenta los salientes rocosos, nos convendrá utilizar los cortes verticales. La leyenda de la Figura 71 hace notar que un paseo aleatorio escalar ya da una idea de la forma de dichos cortes, una idea grosera, claro está, pero que no es en absoluto descabellada como primera aproximación. ¿No tendríamos, en nuestra caja de herramientas de constructores profesionales de modelos, una superficie aleatoria cuyos cortes verticales fueran movimientos brownianos? Hasta ahora no disponíamos de esta herramienta en nuestra caja, pero yo propongo que la introduzcamos: se trata de la función browniana de un punto, B(P), tal como se halla definida por Lévy 1948. Su inventor ha sabido describir maravillosamente sus principales aspectos, sin haber podido (¿o sin haber querido, quizá?) dibujarla; pero para aplicarla a casos concretos, es necesario hacerse una idea intuitiva de ella. Estoy convencido de que el dibujo abajo de la Figura 130 (inferior derecha) de este Ensayo es la primera muestra publicada de la misma.

Primera constatación: su parecido general con la superficie de la Tierra es real pero grosera, todo lo más es aproximado; sin embargo, nos anima a analizar más de cerca hasta qué punto hemos progresado en el estudio de las costas oceánicas, definidas como las curvas formadas por los puntos que se encuentran al nivel del mar. La figura 132, en la parte superior, nos presenta una gráfica obtenida de este modo; nos dan por fin el ejemplo tan buscado de curva carente prácticamente de puntos dobles que, por una parte, tiene una dimensión fractal superior a 1, y que, además, nos recuerda algún lugar del globo terrestre. En este caso concreto, la dimensión es 1,5, y la gráfica nos recuerda mucho al norte del Canadá, las Islas de la Sonda (el parecido aumenta si baja el nivel del mar, con lo que las islas se empequeñecen) o incluso (si el mar baja más aún) al mar Egeo.

El modelo es aplicable también a otros ejemplos, pero los datos de Richardson sugieren en general una D menor que 1,5. Es una pena, puesto que el valor 1,5 hubiera sido fácil de explicar: en efecto, en 1975b demostré que la función B(P) es una excelente aproximación para el relieve, el cual habría sido engendrado por una superposición de fallas rectilíneas independientes.

El modelo generador es el siguiente: se parte de una meseta horizontal, se la rompe a lo largo de una recta elegida al azar, y se introduce una especie de acantilado, una diferencia de nivel aleatoria entre ambos lados de la fractura; después se vuelve a comenzar, y se continua indefinidamente. Al proceder así, se está generalizando al caso del plano la construcción de Poisson indicada al final de la leyenda de la Figura 71. Se ve cómo el razonamiento comprende por lo menos un aspecto de la evolución tectónica, y cómo nos lleva a añadir B(P) a la lista de los azares primarios que hemos comentado en el Capítulo 3.

Sin embargo, al hacer esto, hemos de renunciar a un aspecto que hasta el momento había sido característico de estos azares, a saber, la independencia de sus partes. La discusión de este punto es inevitablemente técnica, y debe ser considerada como una digresión. Consideremos dos puntos, uno al Este y otro al Oeste de una sección Norte-Sur del relieve. Está claro que el conocimiento del relieve a lo largo de la sección reduce la indeterminación que existe en lo referente al punto del Este. Ahora bien, se puede demostrar que dicha indeterminación disminuye también si se conoce el relieve en el punto del Oeste. Si, por el contrario, la indeterminación no hubiera sido afectada, el probabilista habría dicho que el relieve es markoviano, cosa que habría expresado una cierta independencia entre las pendientes de uno y otro lado de la línea Norte-Sur. (Para el tipo irregular de superficies que nos interesan aquí, la idea de pendiente es peligrosa; pero aquí no hay ningún inconveniente en dejar este punto en suspenso). La influencia del relieve del Oeste sobre el relieve del Este expresa que el proceso generador manifiesta inevitablemente una fuerte dependencia global.

Desafortunadamente, repitámoslo, el D que se observa para las costas es en general distinto de 1,5, y ello nos obliga por lo tanto a proseguir nuestra búsqueda si queremos un modelo que tenga una validez más general. Hemos de buscar incluso en una dirección no habitual, pues en el Capítulo 2 me esforzaba por que se aceptara que D había de ser superior a 1, y de ahora en adelante, necesitamos hacerlo descender por debajo de 1,5. Para tener costas menos irregulares, nos hacen falta, por lo tanto, cortes verticales menos irregulares. Afortunadamente, las secciones anteriores de este capítulo nos han preparado bien para esta contingencia, pues dos posibilidades saltan a la vista.

En primer lugar, para tener un modelo de los cortes verticales, basta sustituir la función browniana usual por un ejemplo apropiado de las variantes fraccionarias introducidas más arriba. En efecto, hay superficies aleatorias B_H(P) cuyos cortes verticales son funciones B_H(t). Además, he puesto a punto unos algoritmos que permiten simularlas en un ordenador. La superficie tiene por dimensión 3 − H, y sus secciones planas —entre las que se cuentan las costas, las otras curvas de nivel y también los cortes verticales— tienen dimensión 2 − H todas ellas. No hay ya pues ninguna dificultad para obtener cualquier dimensión que los datos empíricos quieran exigir. Si se prevé D = 1,3, entonces será H = 0,7, valor que justifica nuestra Figura 128. Pero se conocen también ejemplos en los que H y D toman valores próximos a 1 (nuestra Figura 130, izquierda, recuerda la forma de los grandes macizos montañosos), y ocurre a veces que H es casi 0 y D casi 2 (nuestra Figura 130, superior derecha, recuerda las llanuras aluviales inundadas). Así pues, volviendo a la imagen ya utilizada de la caja de herramientas de confeccionar modelos, vemos cómo todas las funciones B_H(P) han de tener un lugar en ella.

Segunda posibilidad: partamos de la construcción de B(P) como superposición de fallas verticales rectilíneas, y acepillemos cada falla de modo que su pendiente aumente y disminuya de manera progresiva. Es posible obtener B_H(P) de esta manera, pero sólo a condición de imponer que el perfil de la falla tenga una cierta forma muy específica, y de la que no es necesario decir que, a priori, no es demasiado natural. Es decir, que la tectónica imaginaria subyacente no es ni muy convincente ni muy explicativa.

A modo de digresión, vamos a esbozar distintas fuerzas susceptibles de efectuar la acción uniformizadora que se traduce en el aumento de H. Con la esperanza de explicar la persistencia «josefina» de los niveles de los ríos, los ingenieros comenzaron por tener en cuenta el agua que pueden almacenar los depósitos naturales de una temporada a otra; se esperaba, por lo tanto, que las descargas anuales de un río variaran más lentamente que lo predicho por la hipótesis de independencia. No obstante, pude demostrar que la acepilladura de las crónicas implicada por este modelo simplificado es en exceso exclusivamente local. Si se tiende a invocar tales fuerzas uniformizadoras para explicar el modelo browniano fraccionario, serán necesarias un gran número de acepilladuras sucesivas, de escalas diferentes. Se podría, por ejemplo, representar el nivel del Nilo como una superposición aditiva de toda una serie de procesos independientes; primero un azar de orden uno, que diese cuenta de los depósitos naturales (ya citados), que no comportase más que interacciones de un año para otro; a continuación, un azar de orden dos, que se calificaría de microclima, y que variase más lentamente aún; luego un clima variable, y así sucesivamente. Desde el punto de vista puramente teórico, hay que seguir así hasta el infinito; pero el ingeniero se detendrá en las escalas de tiempo del orden de magnitud del horizonte (siempre finito) de un proyecto de control de las aguas.

Volviendo ahora al relieve, hay que empezar dándose cuenta (ya era hora) de que es inconcebible que los modelos brownianos funcionen bien globalmente, por la sencilla razón de que la Tierra es redonda. Es cierto que Lévy definió también una función browniana sobre la esfera, pero parece ser que tampoco nos conviene. (P.S. Véase sin embargo Mandelbrot 1977f y 1982f). Lo mejor es, pues, detenerse en las escalas intermedias, admitiendo que las diversas acepilladuras sufridas por el relieve en el curso de la historia geológica tienen unas escalas espaciales cuyo máximo corresponde al orden de magnitud de los continentes. Si se pensara que toda la Tierra corresponde a un único valor de H y de D, habría sido necesario añadir que las intensidades relativas de las distintas acepilladuras tienen un carácter universal; pero si se admite (de un modo más realista) que H varía de un lugar a otro, estas intensidades relativas tendrían, también, un carácter local.

Un nuevo test de la adecuación del modelo browniano fraccionario se obtiene al comparar las distribuciones teórica y empírica de las superficies proyectivas de las islas del océano, es decir, de las superficies medidas después de la proyección sobre una esfera terrestre ideal. Esta definición complicada es inevitable, pues no hay ninguna duda de que, exactamente igual que ocurre con el perímetro de una isla, su verdadera superficie es infinita (o, si se prefiere así, depende del patrón de medida), mientras que la superficie proyectiva S no plantea ningún problema conceptual. Además, la distribución de superficies relativas salta a la vista cuando se mira un mapa; es incluso más evidente que la forma de las costas (pensemos en el mar Egeo). No es pues sorprendente que se haya hecho un estudio estadístico del caso; se encuentra que la distribución de S tiene una homotecia interna, en otras palabras, es una distribución hiperbólica: Pr(S>s) = s^−B. Korcak había sacado la conclusión precipitada de que B = 0,5, pero yo encontré que era necesario un B más general. La simplicidad del resultado de Korcak llamó la atención de Maurice Fréchet; al escucharle se me ocurrió que para explicar este resultado sería suficiente con que el propio relieve tuviera también una homotecia interna, idea que acabó por conducirme al modelo browniano fraccionario del relieve.

Dicho modelo prevé que 2B = D = 2 − H. Si H es muy próximo a 1, las áreas son muy desiguales, en el sentido de que, por ejemplo, la 10.^a isla tiene una superficie casi despreciable en comparación con la de la isla mayor. La desigualdad disminuye con H. Observemos que el B correspondiente al relieve fractal con H = 0,7 cae cerca de los datos empíricos relativos al conjunto de la Tierra.

Los autores que han examinado las áreas de las islas han hecho naturalmente lo mismo con los lagos, y sus resultados merecen también ser estudiados. Resulta que la ley hiperbólica da una representación tan buena como para el caso de las islas. Por consiguiente, un análisis superficial podría llevarnos a la conclusión de que no hay nada nuevo. Sin embargo, si se reflexiona acerca de este problema, esta nueva confirmación parece demasiado buena para ser creíble, pues la definición de un lago no es ni con mucho tan simétrica como la de una isla oceánica. Mientras que estas últimas las hemos podido definir de manera que haya una en cualquier lugar donde el relieve lo exija, la presencia de un lago depende de muchos otros factores: por ejemplo, sólo queda retenido por su fondo si éste es impermeable, y su área (pensemos en el Mar Muerto o en el lago de Chad) varía con la lluvia, el viento y la temperatura ambiente. Además, los sedimentos de los lagos afectan el terreno, suavizando su forma. El hecho de que la homotecia interna sobreviva a todas estas influencias heteróclitas merece, por consiguiente, una explicación particular. Un pesimista se inquieta ante estas dificultades, pensando si no están aún a tiempo de volverse atrás y poner en duda algunos de los resultados obtenidos, como el referente a las islas; por el contrario, un optimista (como yo) saca sencillamente la conclusión de que todas las influencias, aparte de la del relieve, parecen ser completamente independientes de la superficie. (En efecto, el producto de un multiplicando aleatorio hiperbólico por un multiplicador casi completamente arbitrario resulta ser también hiperbólico).

Es de esperar, de todas formas, que algunos matemáticos se interesen algún día por la estructura de los fondos, aunque sólo sea para el caso browniano H = 0,5.

Gran parte de lo que se dijo en el Capítulo 2 acerca de las costas oceánicas se aplica también a las orillas de un río. Sin embargo, la analogía sólo puede ser aproximada. En efecto, habíamos sustituido la instantánea de una costa, que varía con el viento y las mareas, por la curva de nivel cero, que está completamente definida por el relieve. No se puede hacer nada parecido con la orilla de un río; ésta no sólo es función del relieve, sino también de la porosidad del suelo, y de la lluvia y el buen tiempo, no sólo en el instante de la observación, sino a lo largo de todo un período de tiempo muy difícil de determinar. Sin embargo, a pesar de esta cruel falta de permanencia, los sistemas fluviales, al igual que los lagos, resultan tener algunos aspectos muy sistemáticos; ¿no podría ser que, exactamente igual que la distribución de las superficies de los lagos imita la de los fondos del relieve, el sistema fluvial imite los caminos que sigue el agua sobre un terreno lo máximo de accidentado posible, exactamente después de un chaparrón? Creo que las cosas son efectivamente así, pero mi razonamiento no puede desarrollarse aquí. Contentémonos con esbozar (Figura 134) la más simple de dichas corrientes.

LÁMINA 124. Vuelo browniano fraccionario muy persistente

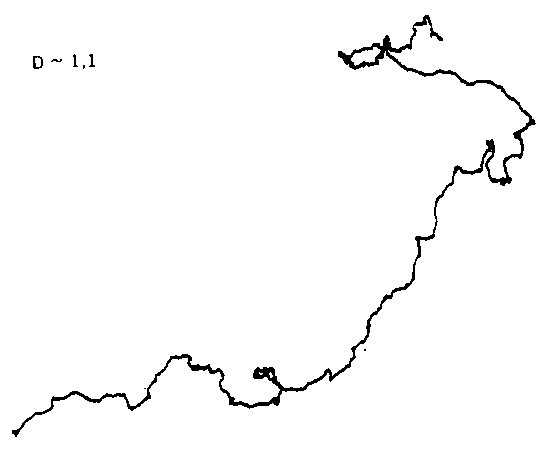
FIGURA 124

Este dibujo constituye un ejemplo de curva fractal, con homotecia estadística interna, cuya dimensión es D = 1/0,9 = 1,1, y en la que la tendencia a la formación de bucles —sin estar prohibida— está muy amortiguada, al haberle impuesto un grado de persistencia muy alto. En esta figura, y en las siguientes, los distintos grados de persistencia son mucho más aparentes que lo que habrían sido en gráficas que representaran la variación de las coordenadas escalares en función del tiempo. Si uno considera estas curvas como el resultado de superponer convoluciones grandes, medianas y pequeñas, en el caso que nos ocupa la intensidad de las últimas es tan débil que son apenas visibles.

LÁMINA 125. Vuelo browniano fraccionario medianamente persistente

FIGURA 125

Partiendo de la figura anterior y sin cambiar la semilla del simulador pseudoaleatorio, hemos aumentado la dimensión hasta D = 1/0,7 = 1,43. Esto equivale a decir que, sin cambiar ninguna de las distintas convoluciones, hemos aumentado la importancia relativa de las pequeñas y (en menor grado) de las medianas. Por esta razón, la tendencia a la formación de pequeños bucles está menos amortiguada, y resultan mucho más manifiestos. Sin embargo, la forma general subyacente se reconoce aún sin dificultad.

LÁMINA 126. Vuelo browniano fraccionario apenas persistente (próximo a un vuelo browniano)

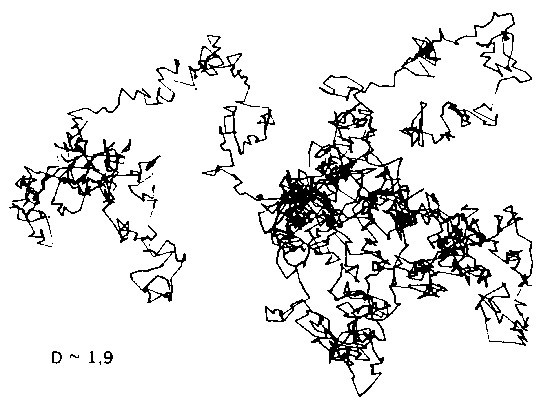
FIGURA 126

Aquí, siempre con la misma semilla, la dimensión se ha aumentado hasta D = 1/0,53, un poco menos de 1,9: se nota la proximidad del límite D = 2, que como ya sabemos corresponde al movimiento browniano normal. En el límite D = 2, se obtendría un modelo matemático del proceso físico de la Figura 57, donde las distintas convoluciones que se le añaden tienen todas la misma importancia relativa («espectro blanco»), por lo menos en media, puesto que el detalle cambia a menudo la muestra considerada. Por ejemplo, la «deriva» de baja frecuencia que dominaba las figuras en el caso de D próximo a 1, tiene una intensidad muy variable cuando D se aproxima mucho a dos; con la semilla utilizada aquí, la deriva es casi invisible; pero no ocurre lo mismo con otras semillas. Por ejemplo, podría ser que, hasta para D cercano a 1 la deriva sea mucho más fuerte que en la Figura 57; en este caso, sigue siendo manifiesta cuando D se acerca a 2.

LÁMINA 128. Vistas de un continente imaginario

FIGURA 128

Yo estaba buscando un modelo de la forma de las costas naturales, y era de esperar que al mismo tiempo serviría para representar el relieve terrestre y también la distribución de las superficies de las proyecciones de las islas sobre la esfera terrestre. Con este objeto, propuse una familia de procesos estocásticos que generan superficies aleatorias; dicha familia depende de un parámetro que se puede escoger arbitrariamente y que no es otra cosa que una dimensión fractal. Esta figura presenta diversos aspectos de una muestra característica, realizada con el ordenador, para la que se ha elegido el parámetro de modo que la dimensión de las costas, así como la de los cortes meridianos, sea D = 1,3. Se deduce de ahí que la dimensión de la superficie sea en total 2,3, de donde se tiene que la verdadera superficie de la isla es infinita, aunque su superficie proyectiva sea finita y positiva.

Para evaluar el grado de realismo del modelo en cuestión, he llevado a cabo distintas pruebas estadísticas «cuantitativas». Todas ellas han sido «positivas», pero en mi opinión esto no es lo más importante, pues la calidad de un modelo científico nunca es, en última instancia, una cuestión de estadística. En efecto, cualquier prueba estadística se limita a un pequeño aspecto de un fenómeno, mientras que lo que se pretende de un modelo es que represente una multiplicidad de aspectos, de los que difícilmente se podría adelantar una lista medio razonable. Para un geómetra, la mejor prueba es, en última instancia, la sensación que el ojo transmite al cerebro. Las gráficas dibujadas con el ordenador son una herramienta insuperable para este fin.

En la Figura 128 se ven diversas vistas de «mi isla» que corresponden a distintos niveles del océano (el procedimiento gráfico empleado sólo es útil bajo esta forma); creo que todas tienen un cierto aire realista, y hasta empiezo a preguntarme en qué lugar, o en qué película de un viaje, he visto otra vez la última de las vistas, con unos islotes como éstos al final de una península como la de la gráfica. Para colmo de suerte, el procedimiento gráfico elegido hace que, en el horizonte, el océano dé la impresión de espejear.

LÁMINA 130. Vistas de continentes imaginarios

FIGURA 130

Para ver si el ojo es tan sensible como digo a la dimensión D de las costas, repitamos el mismo test visual de la Figura 128 con «islas» fractales de otras dimensiones, pero construidas con la misma semilla de generador pseudoaleatorio. En relación a la isla de la Figura 128, se observan diferencias considerables en la importancia relativa de las convoluciones grandes, medianas y pequeñas.

El valor browniano D = 1,5 se halla ilustrado arriba a la izquierda.

Cuando D es demasiado próximo a 1, arriba a la derecha, los contornos de las islas son demasiado regulares, y el relieve presenta demasiadas caras planas inclinadas. Cuando D se acerca demasiado a 2, abajo, para dos niveles diferentes del Océano, los contornos de las islas son demasiado tortuosos, el relieve tiene demasiados picos y abismos al considerarlo en detalle, y es demasiado plano en su conjunto. (Cuando D tiende hacia 2, la costa tiende a llenar todo el plano).

No obstante, hasta las islas que corresponden a D > 1,3 y D < 1,3 nos hacen pensar en algo real; queda pues claro que la dimensión fractal del relieve no es la misma en todas partes; pero rara vez es menor que 1,1 o mayor que 1,5.

P.S. El valor D = 1,3 invocado por las Figuras de la 128 a la 132, se obtuvo comparando imágenes que carecían de detalle —debido a la imperfección de los medios gráficos de 1974—. Posteriormente, la mejora de los grafismos ha conducido a disminuir el valor de D, cosa muy afortunada, pues la Figura 41 sugería valores menores que 1,3.

P.P.S. Voss 1985 describe y compara diversos métodos de síntesis gráfica de paisajes fractales.

LÁMINAS 131 y 132. Costas imaginarias

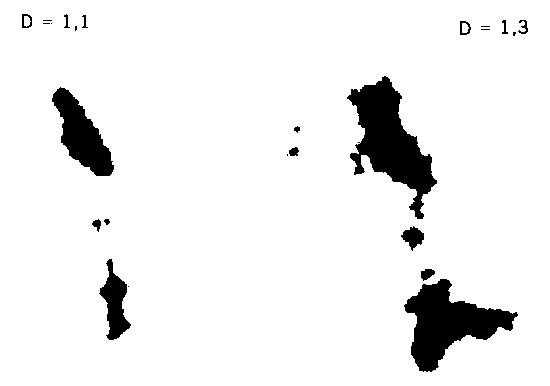
FIGURA 131

FIGURA 132

Las indicaciones de los relieves anteriores se confirman al mirar los siguientes mapas de costas (dibujados por medio de otro programa de ordenador). Cuando D tiende a 2, la costa tiende a llenar todo el plano, como la curva de Peano. Cuando D tiende a 1, la costa se hace demasiado regular para ser útil en geografía. Por el contrario, para D próximo a 1,3, es difícil examinar estas curvas artificiales sin tener la sensación de que se está mirando un atlas: la isla superior recuerda Groenlandia; dándole un cuarto de vuelta (de modo que los números de las páginas queden a la derecha), la isla de la izquierda nos recuerda África; dándole media vuelta, el conjunto nos recuerda Nueva Zelanda, con la isla Bounty incluida. Sucede lo mismo con cualquier otra semilla de generador, en tanto D permanezca cerca de 1,3; si D aumenta hasta 1,5, el juego se hace menos cómodo; cuando D aumenta más aún, el juego resulta mucho más difícil, y hasta imposible.

LÁMINA 134. Red de drenaje fluvial separada casi por doquier. Curva de Peano de las orillas

FIGURA 134

Es interesante considerar aquí otra vez el límite para ε → 0 de la Figura 47, y darle una interpretación de un tipo completamente distinto. Convengamos en decir que un relieve terrestre impermeable está perfectamente drenado a través de su frontera si ocurre que una gota de agua que caiga sobre él acaba siempre por alcanzar un punto de dicha frontera. Habrá puntos tales que, si dos gotas de agua caen al azar en su entorno, sus trayectorias se alejan inmediatamente la una de la otra, por lo menos temporalmente; estos puntos se llamarán de separación. Por ejemplo, un cono perfecto tiene un punto de separación, su vértice, mientras que una pirámide cuadrangular tiene cuatro rectas de separación. Los conos y las pirámides son objetos geométricos clásicos, muy regulares, mientras que nosotros estamos suponiendo que el relieve terrestre es fractal. Resulta, como vamos a demostrar dentro de poco, que los puntos de separación de un relieve natural pueden ser densos por doquier, y corresponder, por lo tanto, a una red de drenaje separada casi por doquier. Al pretender sólo demostrar una posibilidad y no intentar describir el propio relieve, nuestra ilustración se puede tomar la libertad de ser esquemática.

La cuenca será el interior de un cuadro, con los vértices orientados según los puntos cardinales. Las diagonales forman un curso de agua cruciforme, cuya rama principal alcanza el punto S, partiendo de muy cerca del punto N, y cuyas ramas laterales parten de muy cerca de los puntos E y O y desembocan en el centro; cada una de estas cuatro ramas drena un cuarto de la cuenca. En una segunda etapa, se hace una cruz en cada rama; en este estadio, la red consta de 16 secciones de curso de agua, cada una de las cuales tiene una longitud de 1/4 de la diagonal de la cuenca, y drena 1/16 de su superficie. Las fuentes de las ocho sub-ramas coinciden dos a dos (conviene excluirlas de la red, pues de lo contrario ésta tendría puntos dobles). Si se continúa indefinidamente la construcción iniciada ahí arriba, la longitud total de las orillas de todas las ramas habrá aumentado sin fin; el número total de las fuentes —que son puntos dobles (excluidos de la red)— será también infinito, y nuestra red se habrá acercado tanto como queramos a cualquier punto de la cuenca. Si se detiene la construcción después de un número finito de etapas, los afluentes se pueden clasificar en orden creciente, y se constata que su tendencia a la ramificación satisface una regla conocida por los especialistas, debida a Horton.

P.S. Las orillas del río y sus afluentes se unen en una curva que reúne dos puntos situados uno frente al otro en la desembocadura del río. Es una curva de Peano distinta de la curva de la Figura 49. Y recíprocamente, he hecho notar que cualquier curva de Peano puede ser interpretada como la orilla acumulada de un río.

¡Un monstruo ideado en 1890 fue domado en 1975!

Capítulo 7 Modelos del relieve terrestre

Capítulo 7
Modelos del relieve terrestre