En este capítulo, volvemos al estudio de un problema que nos es familiar. Me propongo demostrar que la teoría de la formación de las estrellas y las galaxias debida a Hoyle, el modelo descriptivo de Fournier d’Albe, y (lo que es aún más importante) los datos empíricos, sugieren unánimemente que la distribución de las galaxias en el espacio incluye una amplia zona de homotecia interna, en la que la dimensión fractal es próxima a D = 1. No cabe duda de que esta zona se acaba en las escalas pequeñas, justo antes de llegar a objetos con bordes bien precisos, como los planetas. Pero no es seguro si, a gran escala, esta zona se extiende hasta el infinito, o si, por el contrario se acaba con los cúmulos de galaxias (véase el ejemplo del ovillo de hilo comentado en el Capítulo 1), para seguir con una zona cuya dimensión aparente es D = 3. Según la respuesta a esta cuestión, que es muy controvertida, la zona en la que D < 3 será más o menos vasta, y el propio concepto de dimensión será más o menos útil.

El problema de la distribución de las estrellas, las galaxias, los cúmulos de galaxias, etc., fascina tanto al aficionado como al especialista, y ha sido objeto de un número considerable de publicaciones, pero ocupa un lugar marginal en relación con el conjunto de la astronomía y la astrofísica. Esto se debe sin duda a la falta de una buena teoría; ningún especialista pretende haber conseguido explicar por qué la distribución de la materia celeste es irregular y jerarquizada, como se observa a simple vista y confirma el telescopio. Esta característica es señalada en todos los textos, pero cuando se pasa a los desarrollos serios, la casi totalidad de los teóricos supone inmediatamente que la materia estelar está distribuida uniformemente. Otra explicación de esta resistencia a tratar de lo irregular es que no se sabía cómo describirlo geométricamente; todas las tentativas en este sentido habían tenido que reconocer alguna que otra deficiencia. Por esta razón, no quedaba más remedio que pedir a la estadística que decidiera entre la hipótesis de la uniformidad asintótica, muy bien conocida, y una hipótesis contraria, del todo vaga. ¿Hay que sorprenderse de que los resultados de unos tests tan mal preparados hayan sido tan poco concluyentes?

Para salirse de la rutina, ¿no sería útil intentar, una vez más, la descripción sin aguardar a la explicación? ¿No sería útil demostrar con un ejemplo que las propiedades que se desea encontrar en esta distribución son mutuamente compatibles, y todo ello en el seno de una construcción «natural», esto es, en la que no haya que ir metiendo todo aquello que se quiera obtener, y que no sea demasiado ad hoc, «hecha a medida»? En este capítulo, mediante la utilización de una generalización del movimiento browniano, vamos a demostrar que una construcción de este tipo es perfectamente posible, que parece fácil (después), y que inevitablemente echa mano de los conceptos de objeto y dimensión fractal. Estudiaremos a qué se parece una distribución sometida a un arracimamiento (siguiendo con el neologismo del Capítulo 4) ilimitado cuando se lo observa radialmente desde la Tierra; el resultado, que no es en absoluto evidente, no puede dejar de influir en la interpretación de los datos experimentales. El Capítulo 9 tratará de los objetos relativamente intermitentes e introducirá la materia interestelar; pero, por el momento, supondremos que el espacio entre las estrellas está vacío. (En publicaciones de carácter más técnico Mandelbrot, 1975u, 1979u, 1982f, muestro lo que este marco propuesto por mí aporta al estudio estadístico preciso del problema de la intermitencia galáctica).

Empezaremos examinando de cerca el concepto de densidad media global de la materia en el Universo. A priori, igual que la longitud de una costa, no parece que la densidad vaya a plantear problema alguno, pero, de hecho, las cosas empeoran enseguida y de una manera muy interesante. Entre los muchos procedimientos para definir y medir esta densidad, el más directo consiste en medir la masa M(R) contenida en una esfera centrada en la Tierra de radio R, evaluar después la densidad media definida por M(R)/[(4/3)πR³], hacer luego que R tienda a infinito y definir, finalmente, la densidad media global ρ como el límite al que forzosamente ha de tender la densidad media.

Desgraciadamente, la convergencia en cuestión deja mucho que desear: a medida que ha ido aumentando la profundidad del Universo alcanzada por los telescopios, la densidad de la materia no ha dejado de disminuir. Incluso ha variado de manera regular, manteniéndose aproximadamente proporcional a R^D⁻³, donde el exponente D es positivo y menor que 3, en realidad mucho más pequeño, del orden de magnitud de D = 1. Por lo tanto, la masa M(R) aumenta aproximadamente como R^D, fórmula que nos recuerda a la obtenida en el Capítulo 4 para el número de errores extraños en el lapso de tiempo R, y que nos da, por lo tanto, un primer indicio de que D pudiera muy bien ser una dimensión fractal.

La desigualdad D < 3 indica que, a medida que uno se va alejando de la Tierra, los objetos celestes se agrupan jerárquicamente, manifestando así el intenso arracimamiento del que hemos hablado. En los términos elocuentes de Vaucouleurs 1970 (cuya exposición me ha ayudado muchísimo y recomiendo vivamente), «el arracimamiento de las galaxias y, sin lugar a dudas, de todas las formas de la materia, es, según todos los métodos observables, la característica dominante de la estructura del Universo, sin ningún indicio de que haya una aproximación a la uniformidad; la densidad media de la materia decrece continuamente cuando se consideran volúmenes cada vez mayores… y las observaciones no dan ninguna razón para suponer que esta tendencia no continúe a distancias mucho mayores y densidades mucho más bajas».

Si la tesis defendida por Gérard de Vaucouleurs se confirma (no se puede ocultar que había suscitado reservas, pero parece ser cada vez más aceptada), lo más sencillo será suponer que D es constante. Pero, de todos modos, el Universo en su conjunto se comportaría como el ovillo de hilo comentado en el Capítulo 1: en una zona intermedia, su dimensión sería inferior a 3; a gran escala dicha dimensión sería, según que Vaucouleurs tuviera o no razón, inferior o igual a 3; y en cualquier caso, a muy pequeña escala, desde el punto de vista de la astronomía, se estaría tratando primero con puntos y luego con sólidos de bordes bien delimitados, con lo que D se haría igual a 0 primero, y luego a 3.

Por el contrario, la idea ingenua de que las galaxias se reparten en el Universo de modo prácticamente uniforme (esta idea se traduciría técnicamente en el hecho de que seguirían la distribución de Poisson) nos ahorraría la zona intermedia en que la dimensión está comprendida entre 0 y 3, dando simplemente las dimensiones 3, 0 y 3 (para escalas decrecientes). Si el modelo fractal con 0 < D < 3 sólo se aplica en una zona truncada por sus dos extremos, se podrá decir que, globalmente, el Universo tiene dimensión 3, pero con perturbaciones locales de dimensión inferior a 3 (exactamente igual que la teoría de la relatividad general afirma que, globalmente, el Universo es euclídeo, pero la presencia de materia lo hace localmente riemanniano).

Sea cual sea el valor de las sugerencias hechas hace un instante, conviene preguntarse bajo qué forma matemática —evitando contradecir la física, pero sin esperar que, por el momento, ésta nos pueda proporcionar alguna ayuda— se puede formalizar la idea de que la densidad aproximada de materia tienda hacia cero, anulándose la densidad global. La primera construcción que demuestra la compatibilidad de estas condiciones parece haber sido dada en 1907 por Edmund Edward Fournier d’Albe, un autor de trabajos de «ciencia ficción» disfrazados de ciencia, algunos de los cuales están a la espera de convertirse efectivamente en trabajos científicos. Presentaremos su modelo a partir del original, pues uno no puede fiarse de ninguna de las exposiciones (sarcásticas e incompletas) que se han hecho de él. Su extraña obra, Fournier 1907, sólo ha sobrevivido porque tuvo la suerte de llamar la atención de un astrónomo ya establecido, C.V. L. Charlier, en cuyas manos dio lugar a un modelo más general, pero en realidad menos útil, que describiremos dentro de poco. El principio de este modelo fue discutido por Borel 1922, pero luego cayó en el olvido, para ser reinventado de nuevo por Lévy 1930 y —lo que es más importante aún— por Hoyle 1953. Al igual que Fournier y Charlier, Paul Lévy intentaba evitar la paradoja del cielo en llamas, conocida como «paradoja de Olbers», que apasiona al aficionado y que vamos a tratar. Más tarde, Hoyle desarrolló su modelo de la génesis de las galaxias, que también analizaremos.

Considero conveniente centrar la exposición siguiente en el modelo de Fournier-Charlier, pero no se puede pretender mantenerlo hasta el final, pues es totalmente inverosímil, exactamente igual y por las mismas razones que lo era el conjunto de Cantor para los errores telefónicos: es excesivamente regular, y el origen terrestre desempeña un papel privilegiado en su construcción, cosa que resulta inaceptable, porque es contraria al principio cosmográfico —que también discutiremos.

Este último principio plantea un problema muy serio, pues no sólo es incompatible con el modelo de Fournier-Charlier-Hoyle, sino que también lo es con la idea de que la densidad media en una esfera de radio R tiende hacia 0 cuando R tiende a infinito. He demostrado, sin embargo, que dicha incompatibilidad matemática puede —por decirlo así— ser «exorcizada». Así pues, inmediatamente después de haber descrito el modelo de Fournier, afirmaré que el principio cosmográfico va más allá de lo razonable y de lo que sería de desear, y que debe ser modificado de un modo no por natural menos radical. Recomendaré que se adopte bajo una nueva forma más débil, que calificaré de condicional, postulando que dicho principio sólo vale para los observadores «verdaderos». En apariencia, esta nueva forma débil será sin duda inofensiva, y no cabe duda de que la mayoría de los astrónomos, no sólo la encontrarán aceptable, sino que se preguntarán qué es lo que puede aportar de nuevo; la habrían estudiado desde mucho tiempo atrás si les hubiera despertado el menor interés. Veremos cómo el principio cosmográfico condicional no implica ninguna hipótesis respecto a la densidad global. Para demostrar que permite que la densidad media se comporte como R^D⁻³ alrededor de cualquier observador verdadero, describiré una construcción explícita que, en cierto aspecto técnico, equivale a la sustitución injustificada de un problema de N cuerpos, que es irresoluble, por una combinación de problemas de dos cuerpos, que se puede resolver fácilmente; este procedimiento no pretende tener ninguna realidad cosmográfica, pero resuelve la paradoja que nos interesa. Por el camino, encontraremos muchas razones para interpretar D como una dimensión fractal.

Consideremos 5 puntos, como en la Figura 104, dispuestos en los cuatro vértices de un cuadrado y en su centro; añadámosles dos puntos más, situados respectivamente por encima y por debajo de nuestra hoja de papel, según la vertical del centro, y a la misma distancia de éste que los cuatro vértices del cuadrado inicial: los 7 puntos así obtenidos forman un octaedro regular centrado. Si se interpreta cada punto como un objeto celeste de base, o también como un «racimo de orden 0», el octaedro será considerado como un «racimo de orden 1». Se continúa la construcción del modo siguiente: un «racimo de orden 2» se obtiene aumentando un racimo de orden 1 en un factor 1/r = 7, y tomando cada uno de los 7 puntos así obtenidos como centro de una réplica del racimo de orden 1. Análogamente, un «racimo de orden 3» se obtiene aumentando uno de orden 2 en un factor 1/r = 7, y tomando cada uno de los 49 puntos así obtenidos como centro de una réplica del racimo de orden 1. Así pues, para pasar de un orden cualquiera al siguiente, se aumenta el número de puntos, y también el radio, en un factor 1/r = 7. Por consiguiente, si cada punto tiene la misma masa, que tomaremos como unidad, la función que da la masa M(R) contenida en una esfera de radio R oscila alrededor de la función representada por la recta M(R) = R. La densidad media en la esfera de radio R es aproximadamente proporcional a R⁻², la densidad media global se anula, y la dimensión, definida mediante M(R) ∝ R^D−3, es igual a 1. Partiendo de los racimos de orden 0 se puede también interpolar indefinidamente, por etapas sucesivas; la primera etapa sustituye cada uno de ellos por una imagen del racimo de orden 1, reducida en un factor 1/7, y así sucesivamente.

Se observa que las intersecciones del resultado con cada uno de los tres ejes de coordenadas, así como sus proyecciones sobre estos ejes, son polvos de Cantor, consistiendo cada etapa de su construcción en dividir [0,1] en 7 partes iguales y después arrancar la segunda, tercera, quinta y sexta.

Este Universo infinitamente interpolado y extrapolado tiene homotecia interna, y se le puede definir una dimensión de homotecia, a saber D = log 7/log 7 = 1. E incidentalmente, observamos este nuevo elemento: un objeto espacial puede tener dimensión 1 sin ser una recta ni una curva rectificable, e incluso sin ser de una sola pieza; así pues, una misma dimensión de homotecia es compatible con valores distintos de la dimensión topológica (concepto descrito en el Capítulo 14). Esta posibilidad nos enseña un poco más acerca de la dimensión de homotecia: puede tomar valores enteros «anormales», es decir, superiores a la dimensión topológica. (¡Obsérvese que el antiguo término «dimensión fraccionaria» obligaba a decir que algunos objetos tenían una «dimensión fraccionaria igual a 1 ó a 2»!).

Como veremos más adelante, Fournier y Hoyle avanzaron distintas razones físicas para justificar este D = 1, pero hay que señalar inmediatamente que este valor no es en absoluto inevitable desde el punto de vista geométrico. Aún conservando la construcción a base de octaedros y el valor N = 7, se puede dar a 1/r un valor distinto de 7, obteniendo así M(R) ∝ R^D con D = log 7/log (1/r). Para 1/r es aceptable cualquier valor comprendido entre 3 e infinito, y por lo tanto, D puede tomar cualquier valor entre 0 y log 7/log 3 ~ 1,7712. Y aún más: la elección de N es discutible. Fournier dice que tomó N = 7 sólo para hacer posible un dibujo legible, siendo el «verdadero» valor N = 10²² (no explica el por qué); por el contrario, Hoyle toma N = 5. Sea como sea, dando un D que satisfaga D < 3, es fácil construir variantes del modelo de Fournier cuya dimensión tome este valor.

(Señalemos, sin detenernos en ello, que la estructura infinitamente jerarquizada del Universo de Fournier sólo aparece plenamente si se lo examina desde un punto infinitamente lejano, empleando un instrumento que permita al mismo tiempo ver hasta el infinito y percibir la distancia. Para un observador que forme parte del Universo, y cuyos instrumentos tengan una potencia limitada, permitiéndole ver sólo hasta una profundidad R < ∞, el Universo de Fournier tendrá una apariencia completamente diferente).

Los defectos del Universo de Fournier son innumerables; entre ellos se cuenta el hecho de que es demasiado regular. Éste es un aspecto que corrige Charlier 1908-1922 dejando que N y r varíen de un nivel de jerarquía al siguiente, tomando los valores N_m y r_m. El objeto que se obtiene así, claro está, no tiene ni homotecia interna ni una verdadera dimensión.

Más concretamente, la cantidad log N_m/log(1/r_m), que corresponde al nivel m, puede depender de m. Suponer que se mantiene entre dos cotas que denotaremos por D_min y D_max introduce un tema más: la dimensión física efectiva puede muy bien no tener un valor único y bien determinado, sino solamente un par de cotas (una superior y otra inferior); este tema no puede, sin embargo, ser tocado aquí.

Sea lo que fuere, la condición D_max < 2 (satisfecha por el modelo de Fournier al tomar D = 1) evita la paradoja de Olbers, acerca de la que hablaremos dentro de un instante. Observemos de pasada que Charlier evita precisar la relación geométrica existente entre los objetos de un mismo nivel. Invoca así lo que el Capítulo 3 califica sarcásticamente de azar-invocación, o azar-deseo. No sabríamos conformamos con esto.

Parece ser que Kepler fue el primero en darse cuenta de que la hipótesis de uniformidad en la distribución de los cuerpos celestes es insostenible. Si así fuera, el cielo nocturno no sería negro; tanto de día como de noche, todo el cielo tendría la misma luminosidad que el disco solar, es decir, tendría uniformemente el color del fuego. Esta inferencia se conoce normalmente como «paradoja de Olbers», por referencia a Olbers 1823; para una discusión histórica puede uno dirigirse a las referencias siguientes: Munitz 1957, North 1965 o Jaki 1969. Hemos dicho que la paradoja desaparecería si uno pudiera convencerse de que los cuerpos celestes satisfacen M(R) ∝ R^D con D < 2. El objetivo primero de Fournier y Charlier había sido construir un Universo en el que M(R) tuviera efectivamente esta forma.

El razonamiento de Olbers es sencillo a más no poder: la luminosidad de una estrella, situada a una distancia R del observador, disminuye en la proporción 1/R², pero su superficie aparente es también proporcional a 1 /R², con lo que la densidad de luminosidad aparente será la misma para todas las estrellas. Además, si el Universo es uniforme, casi cualquier dirección trazada en el cielo intersecará el disco aparente de alguna estrella, con lo que la densidad de luminosidad aparente será la misma para todo el cielo. Por el contrario, si M(R) ∝ R^D con D inferior al umbral D = 2, una proporción no nula de las direcciones se pierde en el infinito sin encontrar nada. Ésa es una razón suficiente para que el fondo del cielo nocturno sea negro. Hay que decir inmediatamente, no obstante, que no se trata de una razón necesaria. Hay muchas otras explicaciones, cuyo estudio cae fuera de las intenciones de este libro, pero de todas ellas podemos decir que es lamentable que hayan servido para desviar la atención del estudio del arracimamiento estelar o galáctico.

Hemos de señalar también que, cuando la zona en la que D < 3 va seguida, a una distancia grande pero finita, de otra zona en la que D = 3, el fondo del cielo no será negro, sino que estará ligeramente iluminado.

Volvamos a Fournier. Vemos que es más preciso que Charlier, en tanto que se impone un cierto valor de D, a saber D = 1, valor que le basta y le sobra para evitar la paradoja de Olbers. Lo justifica (pág. 103 de su libro) con un razonamiento muy notable —¡y más aún en 1907 que en 1975!—^[1] que reza como sigue. Utilizando sin demasiados escrúpulos una fórmula que en principio sólo es aplicable para objetos con simetría esférica, supone que en la superficie de cualquier universo visible (de orden arbitrario) de masa M y de radio R, el potencial gravitatorio toma la forma GM (siendo G la constante de la gravitación). Una estrella que cayera sobre este universo tendría, en el momento del impacto, una velocidad de (2GM/R)^1/2. Ahora bien, afirma Fournier, la observación muestra que dichas velocidades están acotadas. (¡Uno se pregunta en qué basaba esta afirmación en 1907; en 1975 su enunciado suena como algo muy nuevo!). Si se quiere que, para objetos celestes de orden elevado, esta velocidad no tienda ni a cero ni a infinito, es necesario que la masa M crezca como R, y no (como en el caso de una distribución de Poisson) como el volumen (4/3)πR³.

Cascada de Hoyle. Justificación de D = 1 por el criterio de estabilidad de Jeans

Definiremos un Universo pentádico de Fournier finito, como el que se obtendría si la construcción de Fournier se basara en N = 5 en vez de N = 7, y no se extrapolara hasta lo infinitamente grande ni se interpolara hasta lo infinitamente pequeño. Vamos a demostrar ahora que tanto el carácter jerárquico de un tal Universo, en la forma de «azar-deseo» debida a Charlier, como el hecho de que la dimensión tenga que ser igual a 1, se pueden deducir de la hipótesis de que las galaxias y las estrellas se han formado por una cascada de fragmentaciones a partir de una masa gaseosa uniforme.

El argumento, debido a Hoyle 1953, es controvertido, pero tiene en cuenta una cierta realidad física. En particular, asocia el hecho de que D = 1 al criterio de equilibrio de las masas gaseosas debido a Jeans. Imaginemos una nube gaseosa de temperatura T y de masa M distribuida con densidad uniforme en un borde esférico de radio R. Hoyle postula que M/R toma efectivamente este valor crítico, que la contracción se detiene al formarse una nube de radio R/5^2/3, después de lo cual la nube se subdivide en 5 nubes iguales, de masa M₁ = M/5 y de radio R₁ = (R/5^2/3)/5^1/3 = R/5. Al terminarse (adrede) la etapa igual que comenzó, en la inestabilidad, irá seguida de una segunda etapa de contracción y subdivisión. Hoyle no elige N = 5 para simplificar la ilustración si no por razones físicas y bien precisas (en las que no nos podemos detener). Jeans demuestra que en el caso crítico en que M/R = JkRT/G (siendo J un cierto factor numérico, k la constante de Boltzmann y G la constante de la gravitación), dicha nube es inestable, e inevitablemente se contraerá y subdividirá.

Se puede demostrar además que la duración de la contracción de orden m es 5^−m veces menor que la de la primera; con lo que, aunque el proceso continuara hasta lo infinitamente pequeño, su duración total seguiría siendo finita, superando como mucho en una cuarta parte la duración de la primera etapa.

Se llega así a las siguientes conclusiones. Primero, que Hoyle encuentra otra vez el principio cantoriano que estaba ya subyacente en Fournier. Segundo, que Hoyle da razones físicas para tomar N = 5. Tercero, que el criterio de estabilidad de Jeans proporciona un segundo camino para determinar la dimensión D, y, cosa interesante, da exactamente el mismo resultado final: la dimensión ha de ser igual a 1. Por otra parte, los argumentos de Hoyle y Fournier no son, sin lugar a dudas, sino dos aspectos distintos de una misma idea. En efecto, se observa que en el borde de la nube inestable de Jeans, GM/R es igual a la vez a V²/2 (Fournier) y a JkT (Jeans). Con lo que V²/2 = JkT, lo cual indica que la velocidad de caída de un objeto macroscópico es proporcional a la velocidad media de las moléculas que da lugar a T.

Uno de los innumerables defectos del modelo de Fournier es que asigna al origen un papel sumamente privilegiado. Es un modelo resueltamente geocéntrico y por ende antropocéntrico («a la antigua»); es contrario al «principio cosmológico» que postula que nuestro tiempo y nuestra posición sobre la Tierra no tienen nada de particularmente especial ni nada de central, sino que las leyes de la naturaleza han de ser las mismas en cualquier lugar y en cualquier instante. Esta afirmación es discutida por Bondi 1952. Más concretamente, lo que aquí nos interesa es la aplicación de este principio general a la distribución de la materia, y además no nos ocuparemos de la teoría (λογοσ), sino solamente de la descripción (γραϕη). Distinguiremos pues, con el nombre de «principio cosmográfico fuerte», la afirmación de que la materia sigue las mismas leyes estadísticas para cualquier sistema de referencia (origen y ejes) desde el que se examine.

La idea es muy tentadora, pero difícil de conciliar con unas distribuciones que distan mucho de ser uniformes. Ya hemos dicho algo acerca de esto en el contexto de los errores de transmisión estudiados en el Capítulo 4. La naturaleza de las dificultades que se encuentran cambian según sea el valor de la densidad global de materia ρ en el Universo: si es nulo, uno se enfrenta con una incompatibilidad de principio, mientras que si ρ es pequeño pero no nulo, las dificultades sólo son de tipo estético y de comodidad. Pero, sea cual sea el valor de ρ, parece importante disponer de un enunciado que esté de acuerdo con una visión del mundo que tenga en cuenta los objetos fractales. Para ello, creo que será útil separar lo que habitualmente se toma como principio cosmográfico, en dos partes, cada una de las cuales será objeto de una sección.

Refiramos el Universo a un sistema de referencia que cumpla la condición de que su origen tiene también masa.

POSTULADO: la distribución condicionada de la masa es idéntica para todos los sistemas de referencia; en particular, la masa M(R) contenida en una esfera de radio R, es una variable aleatoria independiente del sistema de referencia.

Si es necesario, se podrá postular también que los límites, para R → ∞, de R⁻³M(R) y de R⁻³ M(R) son casi seguramente iguales, y que además son positivos y finitos.

Consideremos las leyes de distribución de la materia en un sistema de referencia arbitrario y en otro condicionado por el hecho de que su origen sea material. Si vale el postulado adicional, esta última distribución se deduce de la primera por las reglas usuales del cálculo de probabilidades condicionadas, y la primera se deduce de la segunda tomando la media con respecto a los orígenes distribuidos uniformemente en todo el espacio.

(Hay un punto delicado, digno de ser subrayado entre paréntesis: cuando se integra sobre todo el espacio la distribución uniforme de los orígenes, da una masa infinita y, en consecuencia, no es evidente que vaya a ser posible renormalizar la distribución no condicionada de modo que su suma sea uno. Para que esto pueda hacerse es necesario y suficiente que la densidad media global sea positiva).

Supongamos ahora que el postulado adicional sea falso, siendo nulo el lim_R→∞R⁻³M(R). En este caso, la distribución no condicionada de probabilidad simplemente nos dice que, si se elige libremente una esfera de radio R finito, es casi seguro que estará vacía; cosa que, por muy cierta que fuera, carecería completamente de interés y sería insuficiente a efectos prácticos. Cuando todos los casos interesantes tienen, como aquí, una probabilidad nula, la física matemática ha de encontrar un método que distinga entre ellos. Esto es precisamente lo que hace la distribución condicionada de probabilidad, y es lo que justifica el énfasis que propongo que se continúe dando al principio cosmográfico condicional.

Subdividir en dos partes el principio universal tiene la ventaja filosófica suplementaria de concordar con las maneras de la física contemporánea, separando lo que es observable, por lo menos en principio, de lo que es imposible de verificar y constituye, bien un acto de fe, bien una hipótesis de trabajo. De hecho —como ya he dicho— es muy probable que la mayoría de astrónomos no tengan ningún inconveniente a priori contra el condicionamiento que propongo. Haría tiempo que éste se habría convertido en algo banal si se le conocieran consecuencias dignas de atención, esto es, si se hubiera reconocido que constituye, no un refinamiento formal, sino una auténtica generalización. Así pues, ya sea para apoyar el acto de fe, o para demostrar que la hipótesis de trabajo es simplificadora y, en consecuencia, algo útil, es necesario estudiarla en serio.

Digresión acerca de los lugares de parada del vuelo de Rayleigh y de la dimensión D = 2

La combinación de hipótesis, según las cuales la densidad global se anula mientras que el principio cosmográfico condicional sigue siendo válido, excluye el antiguo modelo de Fournier-Charlier; a primera vista, parece incluso como si dicha combinación contuviera una contradicción interna. Pero demostraré que esto no es sí; la compatibilidad de estas hipótesis será ilustrada de entrada de un modo muy artificial, dando un nuevo papel a un ejemplo que tiene la ventaja de que el lector ya estará familiarizado con él (lo hemos utilizado ya en el Capítulo 3), y que es también muy antiguo, pues se remonta por lo menos a Rayleigh 1880. Su defecto mortal es que no tiene ni la dimensión ni el grado de conectividad exigidos por los hechos. Este modelo irá seguido de otros más realistas.

Supongamos que un cohete parte de un punto Π(0) del espacio, en una dirección distribuida de manera aleatoria isótropa. La distancia entre Π(0) y el punto Π(1), definido por la primera parada después de Π(0), será también aleatoria, respondiendo a una distribución prescrita de antemano. Lo esencial de la misma es que los saltos no toman valores grandes sino muy de vez en cuando, de modo que la esperanza matemática del cuadrado de la longitud del salto, 〈[Π(1) − Π(0)]²〉, sea finita. A renglón seguido, el cohete vuelve a partir hacia Π(2), definido de modo que los vectores Π(1) − Π(0) y Π(2) − Π(1) sean independientes y respondan a la misma distribución. El cohete sigue así ad infinitum. Además, se puede determinar los lugares de parada anteriores Π(−1), Π(−2), etc., haciendo actuar el mismo mecanismo en sentido inverso. Dado que dicho mecanismo no hace intervenir para nada el sentido del tiempo, basta con tomar dos trayectorias independientes a partir de Π(0). Una vez hecho esto, borremos los rastros rectilíneos dejados por los cohetes, y examinemos el conjunto de los lugares de parada sin tener en cuenta el orden en que han ido apareciendo. Por la propia construcción, la secuencia de los lugares de parada sigue la misma distribución cuando se la examina desde cualquiera de log puntos Π(m). Así pues, este conjunto satisface el principio cosmográfico condicional, en un sentido estadístico. Vamos a suponer que en cada lugar de parada se ha «sembrado» un pellizco de materia.

Si el vuelo se limita al plano (como en el Capítulo 3), el conjunto de lugares de parada está repartido casi uniformemente. De hecho, si los saltos responden a una distribución gaussiana, el conjunto de los lugares satisface el principio cosmográfico universal. De cualquiera de las formas, el número de lugares contenidos en una esfera de radio R y centro Π(k) tiene un orden de magnitud de M(R) ∝ R². En el espacio, por el contrario, los Π(k) se hallan repartidos tan irregularmente que se tiene también M(R) ∝ R² en vez de M(R) ∝ R³.

El valor del exponente, D = 2, independientemente de la dimensión del espacio ambiente y de la distribución de los saltos Π(k) − Π(k − 1), es una consecuencia directa del teorema del límite central clásico. Este afirma que, cuando 〈[(k) − Π(k − 1)]²〉, la distribución de la distancia recorrida, Π(k) − Π(0), es asintóticamente gaussiana, sea cual sea la distribución exacta de los saltos Π(k) − Π(k − 1) y Π(k) − Π(0). En el espacio se deduce que la densidad media de los lugares es proporcional a R⁻¹ y tiende hacia cero cuando R → ∞. De hecho, si se elige el origen del sistema de referencia con una probabilidad uniforme en el espacio, se puede demostrar que una esfera de radio R finito no contendrá ningún lugar Π(k). Así pues, vista desde un origen arbitrario, la distribución de los lugares es degenerada, excepto en casos de probabilidad total nula. En resumen, el principio cosmográfico es aplicable para los lugares de parada, pero únicamente en un sentido a la vez estadístico y condicional; más generalmente, a consecuencia de que M(R) crece más lentamente que R³, es necesaria la restricción del principio cosmográfico a una forma condicional.

El hecho de que M(R) crezca como R² concuerda con la idea de que, en uno de los múltiples sentidos formales de la palabra «dimensión», la dimensión del conjunto de los lugares Π(k) es igual a 2. Sin embargo, el vuelo descrito más arriba procede por saltos discretos y no puede por lo tanto tener homotecia interna. Con objeto de poder aplicar el concepto de dimensión de homotecia, tal como lo hemos definido anteriormente para la curva de von Koch y el polvo de Cantor, es necesario hacer continua la variable k; y al mismo tiempo interpolar.

Cuando los saltos de un vuelo de Rayleigh son gaussianos, la interpolación es posible y conduce al movimiento browniano isótropo. Esto puede hacerse por etapas, que recuerdan las de la construcción de von Koch, aunque en nuestro caso estén sometidas al azar. En primer lugar se establecen las posiciones para k entero; después se interpola para k múltiplo de 1/2, con lo que la trayectoria se alarga, y así sucesivamente hasta el infinito. En el límite, el «salto elemental» entre k y k + dk es una variable gaussiana de media nula y variación igual a dk. Sin entrar en detalles, digamos que el movimiento browniano es, en efecto, homotético con dimensión fractal D = 2, tanto en el plano como en el espacio. Resulta de esto que llena el plano de manera densa, mientras que deja el espacio prácticamente vacío.

Pero volvamos a una cuestión que ya planteamos en el caso de las aproximaciones llevadas a un grado extremo, pero finitas, de la costa de Bretaña: dado que el concepto de dimensión implica un paso al límite ¿tiene alguna utilidad cuando k es discreto? Mi respuesta, siempre por consideraciones referentes a la naturaleza de la dimensión física efectiva, es una vez más afirmativa.

Un concepto generalizado de densidad y una observación acerca de la expansión del Universo

Sin perjuicio de la estacionariedad condicional, a cada parada de un vuelo de Rayleigh se le puede asignar una masa elegida al azar, siendo las distintas masas independientes; si se quiere una «distribución uniforme» se elegirán masas iguales. Análogamente, es cómodo pensar que la trayectoria browniana tiene una densidad uniforme δ, si se cumple que la masa entre los puntos de parámetros k' y k es igual a δ|k − k|.

Veamos qué implicaciones tiene esto bajo el punto de vista de la expansión uniforme que, según Edwin Hubble ha demostrado, rige nuestro Universo. Se admite habitualmente que dicha expansión parte de una densidad uniforme δ. Si el Universo está en expansión, δ se modifica progresivamente, pero sin perder nunca la uniformidad. Generalmente, se cree que cualquier otra distribución cambiaría con la expansión, pero basta un solo contraejemplo para demostrar que las cosas no son así. Si se parte de la distribución browniana, la expansión tiene el mismo efecto que en el caso uniforme: δ cambia, pero la uniformidad persiste. Por consiguiente, los lugares de Rayleigh son necesariamente compatibles con la expansión del Universo.

El modelo browniano presenta, por lo menos, dos características inaceptables en cosmografía: es una curva continua, hecho que no se manifiesta en lo más mínimo en las distribuciones estelares, y el valor de su dimensión, D = 2, es mayor que el D ~ 1,3 sugerido por las observaciones. Por consiguiente, para salvar las virtudes del movimiento browniano, incluida la invariancia frente a la expansión del Universo, habrá que modificarlo en algún aspecto esencial.

Lugares de parada de un vuelo de Lévy. Las galaxias consideradas como un polvo fractal de dimensión D < 2

La generalización que propongo sustituye el vuelo de Rayleigh por lo que yo llamo un vuelo de Lévy. Este atribuye una probabilidad no despreciable a los valores muy grandes de la distancia U entre Π(k) y Π(k + 1), de modo que la esperanza matemática (U²) se hace infinita. Más concretamente, para asegurar que los lugares de parada tengan asintóticamente homotecia interna, basta con tomar Pr(U>u) = u^−D; ésta es la distribución hiperbólica que ya nos resulta familiar después del estudio de la distribución de las longitudes de las intermisiones en el Capítulo 4. Para que se cumpla nuestra condición de que (U²) = ∞, se ve fácilmente que es necesario que 0 < D < 2.

El grado de arracimamiento que se sigue de ello está ilustrado en las Figuras 106 a 111, que muestran, bien sea detalles que se ven en proyecciones horizontales sin perspectiva, o bien el mapa de la región «ecuatorial» celeste. A modo de comparación, la Figura 112 presenta una porción del cielo verdadero. Visualmente, el arracimamiento correspondiente a D = 1 es excesivo, mientras que D = 1,3 concuerda bastante bien con las estimaciones de Gérard de Vaucouleurs.

La consecuencia principal de esta nueva ley, Pr(U>u) = u^−D es la siguiente: tanto en el plano como en el espacio (si D < 1, vale también para la recta), la cantidad 〈M(R)〉 es proporcional a R^D, siendo el cociente M(R)/〈M(R)〉 una variable aleatoria independiente de R. En particular, y contrariamente a lo que se constata en el vuelo de Rayleigh, el exponente de un vuelo de Lévy depende explícitamente de la distribución de los saltos. Esto se debe al hecho de que, cuando (U², = ∞, el teorema del límite central clásico deja de ser válido, y tiene que ser reemplazado por un teorema del límite central especial, cuya forma depende de la ley que rige los saltos. El límite constituye la versión tridimensional de una variable aleatoria «estable» en el sentido de Paul Lévy (Capítulo 14). El caso escalar está tratado en el volumen 2 de Feller 1966. El caso tridimensional con D = 3/2 aparece en física en relación con el problema de Holtsmark, discutido por Feller 1966 y por Chandrasekhar 1943. La ley estable correspondiente a D = 1 se denomina ley de Cauchy, y de ahí el nombre «vuelo de Cauchy» empleado en las Figuras 106 y 108.

En resumen, gracias a la posibilidad de controlar la ley que rige los saltos, nuestra elección de la dimensión resulta ser más libre: se puede obtener el valor D = 1 o cualquier otro valor sugerido por los resultados observacionales.

Sin embargo, el modelo cosmográfico que he basado en el vuelo de Lévy no ha de tomarse demasiado en serio; su principal virtud radica en el hecho de que da una demostración, a la vez simple y constructiva, del carácter no trivial de mi generalización condicional del principio cosmográfico.

P.S. Mi modelo ha resultado tener una segunda virtud: las correlaciones teóricas entre las densidades galácticas tomadas entre 2 y 3 puntos del cielo, calculadas en Mandelbrot 1975u, resultan ser idénticas a las que obtiene Peebles 1980 empíricamente. Véase también el P.S. de la pág. 112.

Si un vuelo de Lévy con D < 1 está constreñido a permanecer sobre una recta, sus lugares de parada se parecen al conjunto que se ha obtenido en el Capítulo 4, barajando al azar el orden de las intermisiones de un polvo de Cantor para el que η > 0. La diferencia estriba en que las intermisiones del Capítulo 4 se suceden de izquierda a derecha, mientras que las del vuelo de Lévy son isótropas: van al azar, con la misma probabilidad en ambas direcciones. La razón por la que se ha tenido que hacer isótropa la construcción es evidentemente que la idea de volar de izquierda a derecha no es generalizable ni al plano ni al espacio, al no ser éstos orientables.

Sin embargo, en el caso de la recta, en el que cabe la posibilidad de elegir entre dos métodos, la construcción isótropa introduce complicaciones. En primer lugar, si el origen es un punto del conjunto, los conjuntos de lugares con abscisa positiva o negativa son independientes en el vuelo de izquierda a derecha, pero no lo son en el caso de vuelo isótropo. En segundo lugar, en un vuelo de izquierda a derecha cada salto es idéntico a una sola intermisión. Por el contrario, un vuelo isótropo vuelve constantemente hacia atrás, para posarse en medio del intervalo correspondiente a un salto anterior; por consiguiente, casi cada intermisión resulta de la intersección de varios saltos. Sin embargo, debido a la homotecia interna global, la ley que da la longitud de una intermisión conserva la forma hiperbólica.

Hay otra complicación debida a lo mismo: recordemos que con objeto de establecer la tendencia al «arracimamiento jerárquico», el Capítulo 4 introduce los intervalos llamados «u₀-ráfagas», que separan saltos de longitud mayor que u₀. En la construcción de izquierda a derecha, está excluida la posibilidad de que dos ráfagas tengan puntos comunes. En la construcción isótropa, dicha posibilidad no queda excluida, pero se demuestra que su probabilidad sigue siendo suficientemente pequeña, y tanto más cuanto menor es D, para que se pueda hablar también de ráfagas jerarquizadas.

Volvamos ahora a un punto de vista más físico, para señalar que numerosos autores han dado una explicación diametralmente opuesta a la de Hoyle para la formación de las estrellas y los otros objetos celestes. No invocan una cascada descendente, esto es, la fragmentación de masas muy grandes y muy difusas en pedazos cada vez menores, sino una cascada ascendente, a saber, la aglutinación de un polvo muy disperso en pedazos cada vez mayores. El problema —que volveremos a tratar en el momento oportuno— se parece mucho al que plantean las cascadas en la teoría de la turbulencia. Ahora bien, en este último dominio los resultados más recientes sugieren la coexistencia de ambos tipos de cascada; se puede pues esperar que la disputa confusa entre los partidarios de la fragmentación y los de la coagulación sea resuelta en un futuro no muy lejano.

P.S. El estudio de los agregados fractales se ha convertido en un campo muy activo a partir de 1982.

LÁMINA 104. El universo según Fournier D’Albe

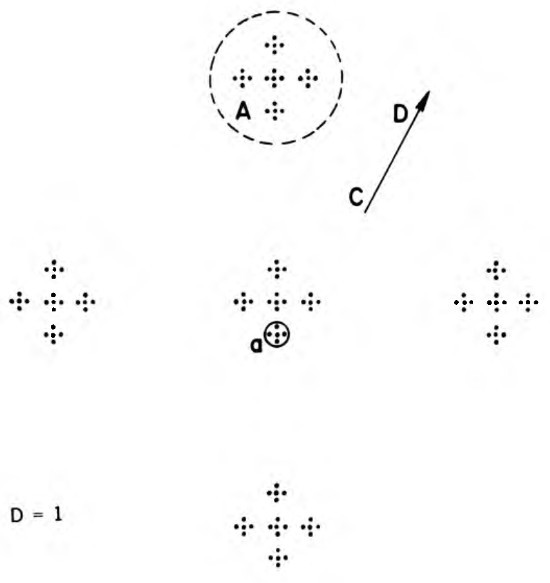
FIGURA 104

Parafraseando la leyenda del original, en Fournier 1907: «Este diagrama describe un multi-Universo basado en un principio cruciforme u octaédrico. Aunque no sea el esquema ni del inframundo ni del supramundo, el esquema es útil, por cuanto demuestra que puede haber una jerarquía infinita de universos homotéticos sin que “el cielo esté en llamas”. Si las menores cruces visibles representan los átomos del inframundo, la figura rodeada por el círculo a representará una estrella del inframundo, esto es, un átomo del nuestro. El círculo A corresponderá a una estrella de nuestro mundo y el todo representará una “superestrella”».

LÁMINA 106. Un universo sembrado de Mandelbrot, de arracimamiento medio. D = 1

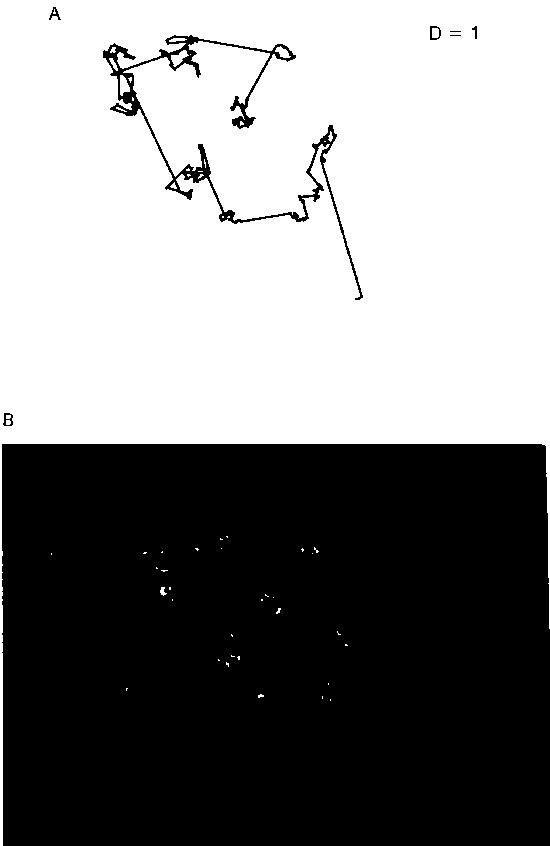
FIGURA 106

Los diagramas A y B de la figura 106 ilustran la simulación por ordenador de un vuelo de Cauchy, y la utilización del mismo para engendrar un Universo «sembrando» un punto en cada parada.

A es una sucesión de segmentos de recta, de dirección isótropa —todos los ángulos tienen la misma probabilidad— y de longitud según la densidad de probabilidad u⁻², que corresponde a D = 1. A la escala de reproducción de esta figura, los segmentos engendrados son en su mayoría demasiado pequeños para ser visibles; en otras palabras, allá donde se ve que se unen dos segmentos visibles, no se tiene un punto aislado sino un pequeño círculo de puntos.

En B se han borrado las líneas generatrices y cada lugar de parada está representado por una «galaxia». Por construcción, si la distribución de las galaxias se examina desde una de ellas, la distribución de las otras es, desde el punto de vista estadístico, exactamente la misma. En este sentido, se puede „considerar legítimamente que cualquier galaxia es el «centro del mundo». Eso es lo esencial del «principio cosmográfico condicional» propuesto en el presente Ensayo. Así pues, el diagrama que tenéis aquí presenta claramente la validez de dos de mis principales temas fractales: a) mi principio condicional es perfectamente compatible con un arracimamiento de apariencia jerárquica y rico en niveles, y b) este arracimamiento y una gran variedad de otras configuraciones de toda clase se pueden manifestar en un objeto en el que nada de esto se había introducido adrede. El grado de arracimamiento que corresponde a la dimensión D = 1 puede ser considerado útilmente como «medio», siendo los correspondientes a D > 1 (Figura 110) y a D < 1, respectivamente, superior e inferior a la «media».

LÁMINA 108. Vista lateral del mismo universo sembrado (D = 1)

FIGURA 108

Precisemos más la figura anterior indicando que se trata de un diagrama espacial que se había proyectado sobre el plano yOz, siendo O la esquina inferior derecha, y estando Oz dirigido verticalmente y orientado hacia arriba. (Las secuencias de las figuras nos obligan a utilizar los ejes de coordenadas no habituales).

Los diagramas A' y B' de la figura 108 son las proyecciones correspondientes al plano zOx, donde O es ahora la esquina inferior izquierda y Oz sigue siendo vertical. Este arreglo pretende ayudar al lector a formarse una idea del carácter espacial de la distribución. Ayudándose de la comparación de A y A', el lector verá cómo el enorme super-super-cúmulo, especialmente rico en niveles jerárquicos, que constituía B, resulta haber sido provocado en buena parte por un efecto de perspectiva, y que en B' se resuelve en un objeto bastante más difuso. Lo mismo ocurre con su «núcleo», que en B parecía compacto pero que en B' está más desecho, en la parte inferior derecha. Por el contrario otros cúmulos se aglutinan.

LÁMINA 110. Un universo sembrado, de arracimamiento inferior a la media. D = 1,5

FIGURA 110

Esta figura representa (como en las figuras anteriores) los saltos y los lugares de parada de un vuelo isótropo cuyos saltos responden a la distribución Pr(U>u) = u⁻¹⁵. La semilla de simulador pseudoaleatorio no se ha cambiado, y la simulación consiste en acortar los largos segmentos interestelares, elevándolos a la potencia 2/3. Esto los acorta tanto más cuanto mayores eran. Además, como hemos escogido la escala de la figura de modo que llenara el espacio disponible, los segmentos menores se han alargado automáticamente. Esta operación disminuye en gran medida la intensidad del arracimamiento, es decir, no sólo disminuye la separación entre los cúmulos sino también el número de niveles jerárquicos aparentes. Para las necesidades de aplicación a la astrofísica, no cabe duda de que se ha ido demasiado lejos en el sentido de que todo parece indicar que la dimensión de las distribuciones estelares está entre 1 y 1,5.

P.S. En 1984 la mejor estimación era D ~ 1,23.

LÁMINA 111. Zona ecuatorial de un universo sembrado, vista desde la Tierra y desde el «Centauro»

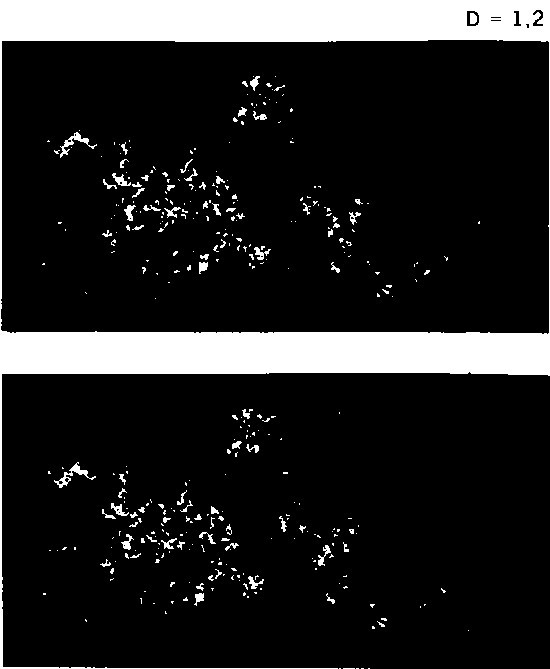
FIGURA 111

Esta figura parte de un conjunto de puntos que fue generado por el mismo procedimiento que los cúmulos aislados representados en las figuras de la 106 a la 110. Sin embargo, la dimensión es D = 1,2. Más importante aún es que aquí se puede ver una misma estructura global, proyectada sobre dos esferas celestes distintas. El centro de la primera es (pongamos por caso) la Tierra, mientras que el centro de la segunda lo podemos llamar «el Centauro», pues es la centésima estrella en el orden de la construcción. En la práctica sólo se han podido representar las zonas ecuatoriales.

LÁMINA 112. La distribución de las galaxias verdaderas

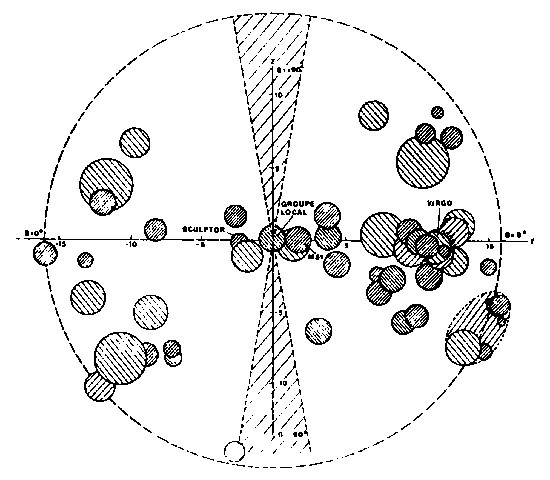
FIGURA 112

Esta figura se refiere a los principales grupos de galaxias cuya distancia a la Tierra es inferior a 16 megaparsecs, y muestra cómo hay un parecido genérico entre la realidad y el modelo descrito en el texto. Visto de cerca, el parecido resulta menos sorprendente (véase el P.S.). Esta gráfica se ha reproducido, con la autorización del editor, de la obra Introduction à la Cosmologie de Jean Heidmann, © 1973 by Presses Universitaires de France.

P.S. La anterior figura 111 muestra cómo mi modelo de Universo sembrado da lugar inevitablemente a grandes vacíos. Los astrónomos me han comunicado inmediatamente que este es el caso, en efecto, con la única salvedad de que el tamaño de los vacíos de la página 111 es excesivo. En la figura 143 se verá como me las he arreglado para obtener un modelo fractal menos «lagunoso».

Capítulo 6 La distribución de las galaxias

Capítulo 6
La distribución de las galaxias