Capítulo 4
Los errores a ráfagas

Este capítulo introduce conjuntos cuya dimensión está comprendida entre 0 y 1 y que están formados por puntos sobre la recta. Para quien tenga que seguir su estudio más allá de donde llegaremos nosotros, estos conjuntos tienen la ventaja de que la geometría de la recta es más sencilla que la del plano o la del espacio, pero tienen en contrapartida dos inconvenientes serios: se trata de polvos tan «tenues» y disueltas que son muy difíciles de dibujar y comparar unas con otras para hacerse una idea intuitiva, aspecto éste que se observará en varias leyendas de figura. Además, el único problema concreto que nos puede servir de soporte es esotérico. El estilo de este capítulo y del siguiente es un poco seco, y el lector puede considerar la posibilidad de saltar inmediatamente al Capítulo 6, que (parafraseando a Henri Poincaré) trata de «problemas que se plantean», más bien que de «problemas que uno se plantea». Sin embargo, este capítulo introduce unos razonamientos que volveremos a tratar más tarde en contextos menos sencillos pero más importantes del plano y del espacio.

La transmisión de los datos

Una línea de teletransmisión es un objeto físico y cualquier cantidad física está sometida inevitablemente a numerosas fluctuaciones espontáneas, que denominamos «ruidos».

Las fluctuaciones que nos interesan ahora se manifiestan especialmente en las líneas de transmisión de datos entre ordenadores, esto es, de transmisión de señales que sólo pueden tomar dos valores: 1 ó 0. Aun en el caso de que la energía relativa del «1» sea muy fuerte, de vez en cuando sucede que el ruido es lo bastante intenso como para deformar el «1» en «0», o viceversa. Por ello, la distribución de los errores refleja la del ruido, simplificándola al máximo, puesto que una función que toma una gran cantidad de valores posibles (el ruido) es sustituida por una función de dos valores: igual a cero si no hay error, e igual a uno si lo hay. El intervalo entre dos errores se llamará «intermisión».

Lo que hace difícil el problema es que se conoce muy mal cómo la distribución de errores depende de la naturaleza física de la línea de transmisión. Sin embargo, en un caso, que discutiremos, el ruido tiene unas características muy curiosas y muy importantes desde el punto de vista conceptual que aquí nos ocupa, así como desde el punto de vista práctico.

Sin entretenernos en este último aspecto, conviene señalar que la misma raíz de los trabajos descritos en este ensayo está en el estudio de los ruidos en cuestión; me interesé en ellos sin imaginarme su importancia teórica futura, porque planteaban un problema práctico importante que escapaba a los métodos ordinarios de los especialistas.

Analicemos, pues, nuestros errores con una finura progresiva. De entrada, se observa que hay horas en el curso de las cuales no hay ningún error. Así pues, todo intervalo de tiempo flanqueado por dos intermisiones cuya longitud es de una hora o más, tiene el aspecto de una «ráfaga de errores», que consideraremos «de orden cero». A continuación, consideremos dicha ráfaga con más detalle. Encontraremos varias intermisiones de 6 minutos o más, que separan unas «ráfagas de errores de orden 1». Análogamente, cada una de estas ráfagas contiene varias intermisiones de 36 segundos, que separan unas «ráfagas de orden 2», y así sucesivamente…, basándose cada ráfaga en intermisiones diez veces más cortas que la anterior. Para hacerse una idea de esta jerarquía va bien examinar la Figura 71. Lo más notable de este resultado es que las distribuciones de cada orden de ráfagas se revelan idénticas desde el punto de vista estadístico, en relación al orden inmediatamente superior. Se descubre así un nuevo ejemplo de homotecia interna, y la dimensión fractal no anda lejos, pero, antes de precisarla, vamos a invertir el orden del desarrollo histórico de las ideas —como en el Capítulo 2— y a examinar primero, no el modelo que recomiendo, sino una variante no aleatoria, muy basta pero, por la misma razón, claramente más sencilla, y más importante por sí misma.

Un modelo basto de las ráfagas de errores: el polvo de Cantor, un conjunto fractal de dimensión comprendida entre 0 y 1

Acabamos de describir el conjunto de los errores quitándole a la recta intermisiones cada vez más cortas. Esto hace pensar en una famosa construcción matemática cuyo resultado es conocido generalmente como conjunto de Cantor, pero que en este libro recibirá la nueva denominación de «polvo de Cantor». El nombre de Georg Cantor domina la prehistoria de la geometría fractal, pero deliberadamente he tardado en citarlo en este ensayo, pues como es bien sabido provoca repulsión entre los físicos. Trataré de demostrar que esta repulsión no es justificada.

El polvo triádico de Cantor se construye en dos etapas: se interpola primero, y luego (etapa menos conocida, pero esencial) se extrapola.

La interpolación va como sigue. Se parte del intervalo [0,1] (la dirección de los corchetes indica que los extremos están incluidos) y se le quita el tercio central, designado por ]1/3, 2/3[ (no comprende los extremos). A continuación, a cada uno de los tercios que quedan, se le quita su propio tercio central, y así sucesivamente hasta el infinito. El resultado final de esta interpolación es tan tenue, que es difícil de representarla gráficamente sin más ayuda. Afortunadamente, es idéntico a la intersección de la «barra de Cantor» (Figura 72) con su eje, o de la curva de von Koch (un tercio de la costa de la isla dibujada en la parte superior de la Figura 43) con el segmento que forma su «base».

Para extrapolar, se dobla repetidamente el número de réplicas del conjunto interpolado. Primero se coloca una réplica en el segmento [2,3], obteniéndose así el conjunto original ampliado en una razón de proporcionalidad 3. Luego se toman dos réplicas en [6,7] y [8,9], obteniéndose así el conjunto original ampliado en un factor 9. Después se disponen cuatro réplicas en los segmentos [2×9, 2×9+1], [2×9+3, 2×9+4 ], [3×9−4, 3×9−3] y [3×9−2, 3×9−1], obteniéndose el conjunto original aumentado 27 veces, y así sucesivamente.

Es fácil ver que el polvo de Cantor tiene una homotecia interna, y que su dimensión es D = log 2/log 3 ~ 0,6309. Además, variando la «regla de disección», se puede llegar igualmente a dimensiones diferentes, aunque siempre comprendidas entre 0 y 1.

Se puede también verificar que, en la porción [0,1] del polvo de Cantor, el número de intermisiones de longitud mayor que u es N(u) ∝ u^−D; más exactamente, N(u) viene representado por una gráfica escalonada que se cruza constantemente con la gráfica de u^−D. ¡Nueva intervención de la dimensión —y nueva manera de medirla—!

Número medio de errores en el modelo cantoriano

Igual que hemos hecho en el caso de una costa, podemos hacernos una idea aproximada de la sucesión de errores que nos preocupa, reiterando el algoritmo cantoriano un número finito de veces. Detenemos la interpolación cuando ésta llega a segmentos de tamaño igual a una pequeña escala interna η, correspondiente a la duración de un símbolo de comunicación, y detenemos la extrapolación a partir del momento que alcanza una cierta escala externa Λ, grande. Finalmente, para obtener una sucesión de longitud superior a Λ, se repite dicha construcción de manera periódica.

A partir de esto, ¿cuál será el número de errores M(R) de una muestra de longitud R creciente? Cuando la muestra comienza en el origen, es fácil ver que, si R se mantiene menor que Λ, el número de errores se dobla cada vez que R se triplica, con lo que el número total de errores crece como M(R) ∝ R^D, y por consiguiente la densidad media de éstos decrece más o menos como R^D−1.

Detengámonos para observar un tema nuevo y esencial. Se conoce cual es el papel que juega D en las expresiones que dan la longitud de un segmento, el área de un disco (interior de un círculo) y el volumen de una bola (interior de una esfera). Pues bien, ¡dicho papel acaba de ser generalizado a valores de D que ya no son necesariamente enteros!

Volvamos a los errores, en el caso de que Λ sea finita (extrapolación detenida): la media del número de errores decrece hasta el valor final no nulo ∝ Λ^D−1, alcanzado para R = Λ, y a partir de ahí permanece constante. Si Λ es infinito, la media disminuye hasta cero. Finalmente, si los datos sugieren un Λ finito y muy grande, pero no permiten una buena estimación del mismo, el límite inferior de la media es no nulo pero queda mal definido y carece, por ello, de utilidad práctica.

Cuando Λ es finito, se puede también hacer que la muestra empiece en medio de una intermisión. En este caso la media empieza siendo nula y lo sigue siendo durante un rato tanto más largo cuanto más larga sea la intermisión. No obstante, acaba por alcanzar para R = Λ, el mismo valor final ∝ Λ^D−1. Cuanto mayor sea el valor de A menor será la media final, y más largo será el período inicial sin errores; más concretamente, dada una duración finita R, mayor será la probabilidad de que entre t y t + R la muestra esté libre de errores. Cuando Λ → ∞, esta última probabilidad tiende a la certeza, planteando así problemas delicados que he resuelto con la introducción del concepto de proceso esporádico, Mandelbrot 1967 b.

Polvo de Cantor truncado y randonizado, condicionalmente estacionario

Las insuficiencias del polvo de Cantor desde el punto de vista práctico son evidentes, debido sobre todo a que su regularidad es excesiva, y a que el origen juega un papel privilegiado, que no está justificado en absoluto. Es por tanto necesario sustituir el polvo de Cantor por un pariente que sea irregular por lo aleatorio y que sólo sería superponible a sí mismo desde el punto de vista estadístico; en la terminología probabilista se le denomina estacionario.

Una manera sencilla de conseguir en parte este objetivo ha sido propuesta por Berger & Mandelbrot 1963. Partiendo de una aproximación truncada del polvo de Cantor, cuyas escalas interna y externa satisfagan η > 0 y Λ < ∞, basta con randonizar (barajar al azar) el orden de sus intermisiones para hacerlas estadísticamente independientes entre sí. Para hacerlo mejor aún, se supone que las intermisiones tienen una longitud entera mayor o igual que 1 y que la proporción de ellas con longitud mayor o igual a u es igual a u^−D (en vez de la función escalonada a la que nos hemos referido más arriba).

En resumen, se parte de las hipótesis de que las intermisiones necesarias son enteros, que son estadísticamente independientes y que la distribución de sus longitudes sigue la ley de «distribución hiperbólica» Pr(U ≥ u) = u^−D, que se lee: «la probabilidad de alcanzar o sobrepasar u es u^−D». La hipótesis de independencia clasifica los errores como formando un «proceso de renovación», llamado también «proceso recurrente». Si el origen es un «punto de recurrencia», el porvenir y el pasado son estadísticamente independientes, pero no lo son si se ha elegido el origen arbitrariamente. Nos encontraremos a menudo con la distribución hiperbólica, pues está íntimamente relacionada con todo lo que concierne a la homotecia estadística.

Vamos a mostrar cómo los errores así distribuidos pueden, en efecto, ser analizados como si formaran ráfagas jerarquizadas. A falta de un término castellano generalmente aceptado (y para no tomar prestado del inglés la palabra clustering, como se hace habitualmente), propongo un neologismo cuyo significado es evidente, y diré que los errores manifiestan un «arracimamiento» muy marcado, cuya intensidad es medida por el exponente D del que hemos hablado más arriba. Para establecer que hay arracimamiento, elijamos un «umbral» u₀; definamos una «u₀-ráfaga» como una secuencia de errores comprendida entre dos intermisiones de longitud mayor que u₀; descompongamos toda la secuencia de errores en u₀-ráfagas sucesivas; distingamos dos tipos de intermisiones: las «u₀-externas» (las que separan nuestras u₀-ráfagas) y las «u₀-internas», y consideremos las duraciones relativas de estas intermisiones, esto es, sus duraciones divididas por u₀. Cuando D es pequeño las duraciones relativas de las intermisiones u₀-externas tienen una gran probabilidad de ser muy claramente mayores que 1 (su cota inferior): por ejemplo, sabiendo que U>u₀, la probabilidad condicional de que U > 5u₀ es 5^−D; con lo que tiende a 1 cuando D tiende a 0. Por el contrario, las duraciones relativas de las intermisiones u₀-internas son, en su mayoría, muy inferiores a 1. Esto es lo que hace que sea razonable la conclusión de que las u₀-ráfagas están claramente separadas, y lo que justifica precisamente el empleo del término de «ráfaga»; además, el mismo resultado vale para cualquier u₀, y por consiguiente, las ráfagas están jerarquizadas. Sin embargo, a medida que D va aumentando, la separación entre ráfagas es cada vez menos acentuada.

Resulta muy notable (Berger & Mandelbrot 1963) que los conjuntos así obtenidos representan sumamente bien nuestros datos empíricos acerca de los errores de transmisión. Además, diversos cálculos referentes al polvo de Cantor se simplifican considerablemente. Empecemos por suponer que Λ < ∞ y calculemos el número medio de errores en el intervalo comprendido entre t y t + R, siendo R mucho mayor que la escala interna η, y mucho menor que la escala externa Λ. Conviene proceder en dos etapas. Se supone primero que hay un error en el instante t, o más generalmente, que entre t y t + R el número M(R) de errores es por lo menos igual a 1. Los valores así calculados no son absolutos sino condicionales. Se encuentra que el valor medio condicional de M(R) es proporcional a R^D, y por lo tanto independiente de Λ, y que la relación entre M(R) y su valor medio es independiente de R y de Λ. Sin embargo, lo esencial es la forma bajo la que se introduce la dimensión en la distribución condicional de M(R). En un polvo de Cantor, todo dependía de la posición de t con respecto al origen. Aquí, por el contrario, toda distribución condicional es invariante con respecto a la posición de t, de ahí la conclusión de que M(R) ∝ R^D vale para todo Λ >> R y sigue valiendo cuando Λ se hace infinitamente grande.

Lo que depende fuertemente de Λ es la probabilidad de que el número de errores sea nulo. En particular, para grandes valores de Λ, la probabilidad de que el intervalo comprendido entre t y t + R caiga todo él en una intermisión de longitud enorme, se aproxima a 1, y la probabilidad de observar un error se hace infinitamente pequeña. Pero esto no afecta en nada la probabilidad condicional del número de errores, siendo la condición o bien que haya un error en el preciso instante t, o bien que haya un error en algún instante entre t y t + R. Reanudaremos esta discusión en el capítulo siguiente, a propósito de lo que llamaremos «principio cosmográfico condicional».

Polvo de Lévy obtenido a partir de una recta a la que se han arrancado «mordiscos» al azar

Volvamos al conjunto postulado por Berger & Mandelbrot 1963. Sus defectos como modelo de la distribución de errores eran que la representación seguía siendo imperfecta en sus detalles, que la restricción a η > 0 era estéticamente molesta, y que la propia construcción era demasiado arbitraria como para que uno se quedara satisfecho con ella. Además, su espíritu se alejaba demasiado del de Cantor. Por ello propuse muy pronto una alternativa que resultó ser mejor en todos los aspectos (véase Mandelbrot 1965c). Consiste en sustituir el polvo de Cantor por una variante aleatoria denominada «polvo de Lévy». La definición clásica resulta de reinterpretar la distribución hiperbólica Pr(U ≥ u) = u^−D hasta aquí hemos supuesto que u es un entero mayor o igual que 1, mientras que Lévy supone que u es un número real positivo. Como resultado de esto, la «probabilidad» total ya no es igual a 1, ¡sino infinita! A pesar de las apariencias, esta generalización tiene un sentido preciso pero implica diversas dificultades técnicas que conviene evitar. Haremos esto adoptando otra construcción más natural propuesta, por Mandelbrot 1972z.

Para introducirla, es útil describir la construcción de Cantor mediante «mordiscos virtuales». (Puede que este método sea inédito, pues hasta ahora no había tenido ninguna finalidad). Se parte también de [0,1], al que se le arranca también el tercio central ]1/3, 2/3[, pero después de esto se arranca los tercios centrales de cada tercio de [0,1]. Como el tercio central de [0,1] ya ha sido arrancado previamente, arrancarlo por segunda vez no tiene efecto real alguno, pero tales «mordiscos virtuales» resultan ser muy cómodos. Se arranca también el tercio central de cada noveno de [0,1], de cada veintisieteavo, etc… Hay que señalar aquí que el número de mordiscos de longitud mayor o igual que u resulta ser igual a (1 − D)/u, siendo D una constante determinada por las reglas de disección.

Dicho esto, randonicemos las longitudes y las posiciones de los mordiscos mencionados anteriormente. Los elegiremos independientemente unos de otros, y de tal manera que el número medio de mordiscos de longitud superior a u sea (1 − D)/u. Al elegirlos independientes, está permitido que los mordiscos se solapen o que sean virtuales en el sentido definido en el párrafo precedente. Los detalles técnicos importan poco, lo esencial es que el resultado de la construcción depende radicalmente del signo de D.

Cuando D ≤ 0 y nos detenemos en mordiscos de longitud η > 0, es poco probable que quede nada; si queda algo, será sin duda un solo intervalo. Si hacemos después que η tienda a 0, es prácticamente seguro (llegando la probabilidad a ser igual a 1) que los mordiscos no dejan casi ningún punto de la recta real por cubrir.

Por el contrario, cuando 0 < D < 1, los mordiscos dejan indefinidamente sin cubrir un conjunto muy tenue, que resulta ser precisamente un polvo de Lévy de dimensión D. Este conjunto presenta una homotecia interna estadística uniforme, en el sentido de que la razón r puede ser elegida sin condicionamientos, contrariamente a lo que ocurría con el conjunto de Cantor, para el que r había de ser de la forma 3^−k, siendo k un entero.

Es una lástima que (como ya se ha dicho al principio de este capítulo) no haya ningún buen método directo para ilustrar los resultados del último párrafo. Sin embargo, exactamente igual que uno puede imaginarse muy bien un polvo de Cantor de manera indirecta, como intersección de la curva de von Koch con su base, uno puede imaginarse también el polvo de Lévy por un método indirecto, mediante la ciudad de calles aleatorias representadas en la Figura 74. La construcción prolonga cada mordisco de la recta en una dirección del plano escogida al azar. Mientras las «casas» que queden tengan una dimensión D > 1, su intersección con una recta arbitraria será un polvo de Lévy de dimensión D − 1. Por el contrario, si D < 1, es casi seguro que la intersección será vacía.

P.S. Los físicos comprenden muy bien la naturaleza de los ruidos clásicos, que dominan la transmisión de señales débiles. El más importante y mejor conocido es el ruido térmico. Pero el problema que nos preocupa aquí concierne a señales tan intensas que los ruidos clásicos son relativamente insignificantes. En consecuencia, los ruidos significativos son no clásicos, difíciles, y seguimos sin comprenderlos bien. Quizá por ello sean apasionantes. El argumento fractal esbozado en este capítulo contribuye a su comprensión.

LÁMINA 71. Movimiento browniano escalar. Sus ceros y su gráfica

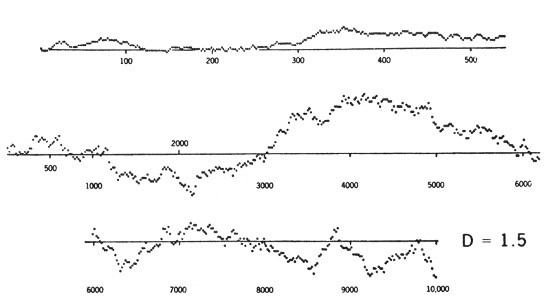
FIGURA 71

La figura de la primera línea representa la secuencia completa de las ganancias acumuladas por «Pedro» jugando contra «Pablo», durante 500 lanzamientos consecutivos de una moneda; se supone que está siempre bien equilibrada (que la cara y la cruz son equiprobables) y que Pedro (resp., Pablo) gana un duro cuando sale cruz (resp., cara). Se sigue de ahí que la ganancia acumulada de Pedro realiza un vagabundeo (=paseo aleatorio) sobre la recta; se trata de una aproximación discreta de un movimiento browniano escalar. Las líneas segunda y tercera representan también las ganancias acumuladas de Pedro si la misma partida llega hasta los 10.000 lanzamientos consecutivos. Para mayor claridad del dibujo se han anotado sólo a intervalos de veinte tiradas. Esta figura procede de un manual célebre (Feller 1950), y se ha reproducido con la autorización de los editores.

El examen repetido de estas curvas ha jugado un papel decisivo en la elaboración de las teorías escritas en este Ensayo. Consideremos, de entrada, sólo los ceros de nuestra función, es decir, aquellos instantes en que las fortunas de Pedro y de Pablo vuelven a su estado inicial. Aunque los intervalos entre estos ceros sean independientes, parece como si sus posiciones estuvieran agrupadas según ráfagas jerarquizadas bien diferenciadas; por ejemplo, cada cero de la primera línea, es reemplazado en la segunda por toda una ráfaga de puntos; si se tratara del movimiento browniano matemático se hubiera podido seguir subdividiendo así las ráfagas indefinidamente. Esta jerarquía se me ocurrió cuando trataba del problema de los errores telefónicos examinados en el Capítulo 4. Se sabía que estos errores están agrupados en ráfagas, pero yo quería verificar si los intervalos entre errores eran independientes o no. Un estudio empírico confirmó esta conjetura, y condujo a los modelos comentados en el texto. Obsérvese que los ceros del movimiento browniano —del que esta Figura es una aproximación— constituyen la variante más simple de un polvo de Cantor aleatorio de dimensión D = 0,5. Cualquier otra D que se desee —siempre que esté compredida entre 0 y 1— puede obtenerse mediante los ceros de otras funciones aleatorias. Por medio de este modelo, se define la dimensión fractal de una secuencia de errores telefónicos: su valor depende de las características precisas del substrato físico.

Examinemos a continuación, no sólo los ceros de la gráfica de ahí abajo, sino el conjunto de sus valores. En 1963, hice notar que su forma recuerda las secciones verticales del relieve terrestre. Después de varias generalizaciones, esta observación condujo a la sucesión de modelos descrita en el Capítulo 6

Un proceso de Poisson. Los instantes en los que Pedro y Pablo juegan, no están necesariamente distribuidos uniformemente en el tiempo; se los puede elegir al azar independientemente unos de otros, con la misma densidad; en este caso, forman un proceso de Poisson. El resultado no difiere sino imperceptiblemente del vagabundeo de más arriba pero presenta ciertas ventajas; en particular, como veremos en el Capítulo 6, su construcción se generaliza al caso multidimensional.

LÁMINA 72. Barra de Cantor

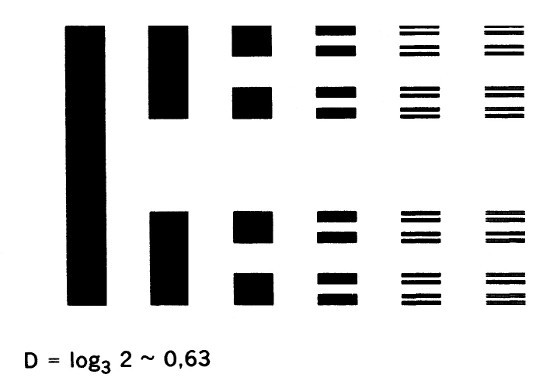
FIGURA 72

Esta barra que se pulveriza, corta su eje longitudinal según un polvo de Cantor, conjunto tan tenue que no se puede ilustrar directamente.

LÁMINA 73. Escalera del diablo

FIGURA 73

El nombre matemático oficial de la función y = f(x) ilustrada en esta figura es «función de Lebesgue del polvo de Cantor». En cada una de las intermisiones de ésta, f(x) es constante. En la aplicación práctica discutida en el Capítulo 4, Δx es un intervalo de tiempo, siendo Δy la energía del ruido durante este intervalo. Es cómodo tratar dicha energía como si estuviera distribuida uniformemente según la vertical. La función inversa x = f⁻¹(y) indica cómo se rompe esta regularidad, se puede decir que se «fractaliza» en una distribución muy irregular.

Una generalización de f⁻¹ en el plano o en el espacio tridimensional está implícito en el estudio de los vuelos de Lévy, ilustrados entre las Figuras 106 a 111. Hay que imaginarse k como coordenada perpendicular al plano de una de tales figuras y el peldaño k-ésimo de la escalera paralelamente a un salto del dibujo situado a la altura k. Si la repartición de la masa galáctica se supone uniforme a lo largo del eje de las k, la función f⁻¹ la convierte en algo terriblemente no uniforme en el plano o en el espacio.

LÁMINA 74. Efecto de los mordiscos en forma de banda: la ciudad de calles aleatorias

FIGURA 74

El plano es recorrido por bandas de dirección isótropa, tales que la intersección de la vertical con la banda de clase ρ tiene longitud Q/ρ = (2 − D)/ρ. El diagrama corresponde a D próximo a 2; su intersección con una recta cualquiera es un polvo de Lévy de dimensión D − 1 próxima a 1. Si se sigue indefinidamente el mismo procedimiento la superficie que «queda» para las casas tiene área nula. (¿Habrá que construir torres de altura infinita?). Cuando Q pasa de 2, las «calles» lo ocupan todo y no queda lugar para las «casas».