Capítulo 3
El papel del azar
Este capítulo continúa con la discusión del problema concreto que se ha abordado en el Capítulo 2, e inicia la discusión del segundo término que aparece en el subtítulo del Ensayo.
Utilización del azar para mejorar el modelo de costa constituido por la curva de von Koch
Aunque nos haya podido servir para evocar un mapa verdadero, la curva de von Koch tiene dos defectos, que encontramos casi sin variación en los primeros modelos de los otros fenómenos de carácter fractal estudiados en este ensayo: sus partes son idénticas entre sí, y las razones de homotecia interna tienen que formar parte de una escala estricta, a saber: (1/3), (1/3)2, etc. Se podría pensar en mejorar el modelo complicando el algoritmo, aunque conservando su carácter totalmente determinista, pero este método no sólo sería fastidioso, sino que además estaría mal inspirado. Está claro, en efecto, que una costa cualquiera ha sido moldeada, con el paso del tiempo, por múltiples influencias, que no es cuestión de seguir al detalle. La situación es aún más complicada que cuando la mecánica trata con sistemas de un número inmenso de moléculas, pues las leyes que rigen el movimiento de éstas a nivel local son conocidas con el máximo detalle, y es su interacción a nivel global la que se conoce mal, mientras que en geomorfología, tanto lo global como lo local son inciertos. Así pues, la solución tiene que ser estadística con mayor motivo que en la mecánica.
Recurrir al azar de esta manera evoca inevitablemente toda clase de inquietudes casi metafísicas, pero no nos vamos a preocupar por ellas. Este ensayo sólo invoca el azar tal como nos lo enseña a manejar el cálculo de probabilidades, porque es el único modelo matemático a disposición de quien pretende entender lo desconocido y lo incontrolable. Afortunadamente, este modelo es a la vez extraordinariamente potente y muy cómodo.
Azar simplemente invocado y azar plenamente descrito
Apresurémonos a subrayar que, para describir una variante probabilística del modelo de von Koch, no basta con decir que «sólo hay que barajar las distintas partes, variando sus tamaños». Este argumento se encuentra a menudo, pero pensar e invocar así el azar es más fácil que describir las reglas que permiten realizarlo. Para ser más precisos, la pregunta que se plantea en primer lugar es ésta: sabemos que el azar puede engendrar irregularidad, pero ¿es capaz de engendrar una irregularidad tan grande como la de las costas, cuyo modelo pretendemos construir? Resulta que, no sólo puede, sino que además es muy difícil, en muchos casos, impedir que el azar vaya más allá de los deseos de uno.
En otras palabras, parece como si se tendiera a subestimar el poder del azar para engendrar monstruos. El error se debe, al parecer, al hecho de que el concepto de azar del físico ha sido moldeado por la mecánica cuántica y la termodinámica, dos teorías en cuyo seno el azar interviene a nivel microscópico, donde es esencial, en tanto que a nivel macroscópico es «benigno». Defino este último término (y hablo de él largamente) en otras publicaciones, y en particular, en un ensayo aún inédito acerca de las Nuevas formas del azar en las ciencias (retomado en parte én Mandelbrot & Vallis 1968 y en Mandelbrot 1973). Por el contrario, en el caso de los objetos físicos que nos ocupan, la homotecia interna hace que el azar tenga la misma importancia a cualquier escala, con lo que no tiene ningún sentido hablar de los niveles macroscópico y microscópico. Por consiguiente, el nuevo grado de irregularidad que, en una construcción cierta (sin azar) como la de von Koch, había tenido que ser introducido artificial y patológicamente, puede muy bien, en el caso de una construcción aleatoria, resultar casi inevitable. Esta última observación es debida a dos autores. Fue Jean Perrin quien señaló la analogía cualitativa entre el movimiento browniano de una partícula (Figura 57) y la curva sin derivada de Weierstrass, y fue Norbert Wiener quien transformó esta analogía en una teoría matemática. El precursor había sido Louis Bachelier, que había introducido en 1900 un modelo de la Bolsa de París (episodio expuesto en el Capítulo 15).
Rastro dejado por el movimiento browniano. Razón por la que no constituye un modelo aceptable de costa
Definamos pues el movimiento browniano P(t), donde P es un punto del plano, para poder explicar luego por qué su «rastro» no sirve como modelo de costa. El movimiento browniano es esencialmente una sucesión de pequeños desplazamientos mutuamente independientes e isótropos (todas las direcciones son igualmente probables). Bajo el punto de vista de este capítulo, lo más sencillo es caracterizar P(t) por medio de las aproximaciones obtenidas tomando un compás de abertura fija η: sea cual sea η, los pasos sucesivos de un movimiento browniano tienen direcciones mutuamente independientes e isótropas. La definición usual es menos directa. Para cualquier par de instantes t y t' > t, se define el vector desplazamiento como el que va de P(t) a P(t'), y se hacen las siguientes hipótesis:
a) La dirección y longitud de este vector son independientes de la posición inicial P(t) y de las posiciones correspondientes a los instantes anteriores a t.
b) Es un vector isótropo.
c) Su longitud es tal que la proyección sobre un eje cualquiera obedece la distribución gaussiana, de densidad
(2π|t' − t|)−1/2 exp(−x2/2|t' − 1|)
El «rastro» trazado por el movimiento browniano ha adquirido el derecho a ser considerado en lo sucesivo como uno de los «azares primarios» que describiremos de inmediato. Desafortunadamente, no nos conviene como modelo de costa, por ser, con mucho, demasiado irregular. En particular, tiene una cantidad innumerable de puntos múltiples, incluso en el sentido estrictamente matemático del término, lo que, por supuesto, es inaceptable para una costa. Se trata de una de esas curvas extraordinarias que —como la curva de Peano del Capítulo 2— recubren todo el plano. Se la puede obligar a carecer de bucles, pero no lo haremos hasta el Capítulo 7.
El concepto de azar primario
Mientras tanto, creo que será útil —por lo menos para algunos lectores— decir algo acerca de las razones (profundas, variadas, y en el fondo poco conocidas aún) que hacen que muy a menudo el resultado de operaciones deterministas imite lo aleatorio, descrito por el cálculo de probabilidades.
La pregunta se plantea ya de un modo particularmente ejemplar en el contexto de lo pseudo-aleatorio que se simula en un ordenador, de manera deliberada y artificial. Es así como los dibujos supuestamente aleatorios que se pueden encontrar a lo largo de este libro han sido construidos, casi todos, de una manera perfectamente determinada. El procedimiento combina de modo indirecto los términos de una sucesión suficientemente larga de números, que se tratan como si fueran los resultados de tiradas de un dado de diez caras (de 0 a 9), obtenidas, sin embargo, de modo repetible por un pseudo-dado programado en el ordenador. Se parte de un solo número que se fija arbitrariamente (el número de teléfono del programador, pongamos por caso), que se denomina semilla. La imagen es clara (e imposible de cambiar en lo sucesivo), pero expresa muy mal la intención de alguien que pretenda simular el azar, ya que, si bien cualquier hortelano espera que su cosecha no dependa sólo del suelo, sino sobre todo de lo que siembre, yo espero que la elección de la semilla no tenga ningún efecto notable en mis simulaciones. Por consiguiente, el pseudo-dado de diez caras constituye una especie de base obligatoria de cualquier simulación. Su fundamento es de carácter universal y, para justificarlo, hay que hacer intervenir la interfase entre la fundamento de números y el cálculo de probabilidades. En cuanto a su aplicación, es muy variable según lo que se ponga en juego, y exige, por parte de los que la estudian, una presencia de espíritu muy distinta; a eso se debe una división muy natural del trabajo entre los especialistas de su fundamento, entre los que no me incluyo, y los de su aplicación, entre los que me cuento.
Todo esto hace comprender mejor cómo el sabio ataca lo pseudo-aleatorio natural. Ahí también se ve, en general, como se distinguen dos estadios que exigen actitudes muy diferentes. Sin embargo, no hay una base universal independiente de la naturaleza del problema y de la manera de abordarlo; uno se las ha de tener, según el caso, con un «azar primario» u otro, entre un gran número de posibilidades. El que es invocado más a menudo sigue siendo el dado, que hay que interpretar aquí como objeto físico idealizado, pero hay muchos otros, como, por ejemplo, puntos cayendo sobre una circunferencia con una distribución de probabilidades uniforme, o estrellas distribuidas en el cielo de modo estadísticamente uniforme (relacionado con la ley de Poisson). Nótese que, cuando no sólo hay una, sino dos o más variables, o incluso una infinidad, como cuando se trata de caracterizar una curva, la hipótesis primaria consiste en suponerlas independientes; tal es el caso del movimiento browniano.
Sea lo que fuere, lo que caracteriza un azar primario es que hace de punto de separación entre dos estadios de una teoría: su base teórica, de la que no diremos casi nada en este libro, y su aplicación, que va a consistir en sustituir unas formas inesperadas del azar por otras formas con las que uno se encuentra ya familiarizado.
LÁMINA57. Ejemplos de movimiento browniano verdadero, y caos homogéneo
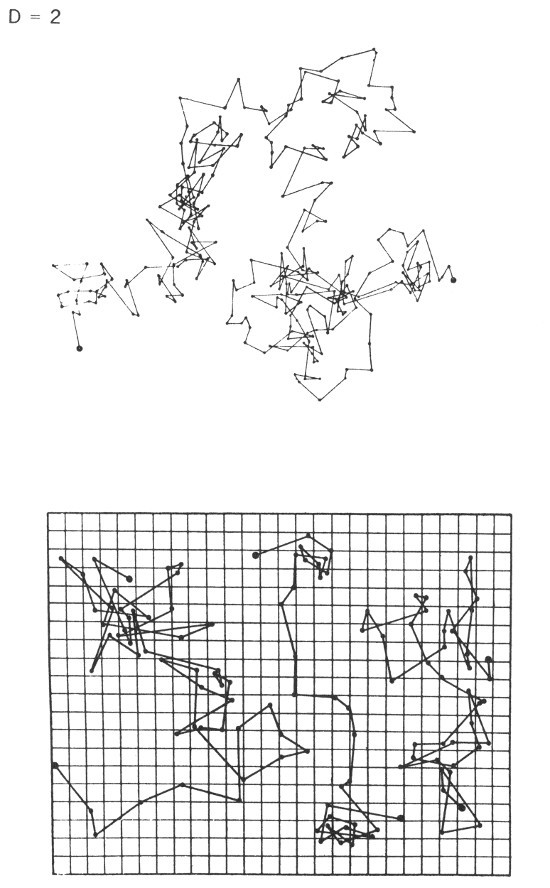
FIGURA 57
Esta figura reproduce algunos ejemplos de movimiento browniano plano (a saber, tres detalles y un trozo grande) según Les Alomes de Jean Perrin. Se trata aquí de un proceso físico y no sólo de su modelo matemático: cada segmento une artificialmente las posiciones sucesivas, en el plano focal de un microscopio, de una partícula sometida a choques moleculares. Si se mirara la trayectoria con más detalle, en instantes doblemente próximos, cada salto sería reemplazado por dos saltos de longitud total superior. En el modelo matemático, dicho alargamiento continúa indefinidamente y, en consecuencia, la longitud total de una muestra es infinita. Por otra parte, su superficie es nula. No obstante su dimensión es D = 2, y (en cierto sentido) recubre el plano de manera uniforme. Éste es uno de los sentidos múltiples que permiten decir que el «caos» representado por el movimiento browniano es homogéneo. (Según la perspectiva que adquiriremos en el Capítulo 6, se trata aquí de un vuelo de Rayleigh en primera aproximación, para el que U2 sería una variable exponencial).
